模拟多孔介质中的达西流和非达西流

从大规模的地质区域到纳米尺度的结构，多孔材料的流动发生在所有长度尺度上。虽然达西定律已经涵盖了许多应用，但是在工业应用中，速度场和压力梯度之间的关系不再是线性的，达西定律不能提供准确的结果。在这篇博文中，我们将更深入的研究多孔介质中可能出现的不同流动状态，以及如何描述它们。

在微观尺度上模拟多孔介质中的流动

为了更深入地理解流经多孔材料中的流动特征，有必要仔细研究它的微观结构。这样我们不仅能更深入的理解多孔材料，也有信心使用宏观方法来模拟多孔材料中的流动。

下面的动画显示了一个大小为 2 cm × 2 cm × 6 cm 的复杂多孔结构，以及使用线性纳维-斯托克斯方程计算的流型。

小型多孔块中的流型。

这些多孔块中包含低流速和高流速的区域，也包含根本不发生流动的区域。即使结构是不规则的，当放大另一个位置的相同多孔结构样品时，其流动特性也是相同的。因此，这被称为 代表性单元体积（REV）。对代表性单元体积进行平均可以得到宏观方程，详见下一节内容。

为了表征流动并获得有关宏观方程的信息，下面几个数值很重要：

• 孔隙率 \epsilon_p=\frac{V_\textrm{pore}}{V_\textrm{tot}}，描述了孔隙体积与总体积的比率，可以从几何形状计算
• 沿流动方向（纵向）下降的压力 \Delta p/L，可以计算或预定义
• 表观速度 u=\frac{Q} {A}，或通过结构的体积流量 Q (m³/s)，除以总横截面积 A(m² )

宏观尺度的流动

达西定律是描述多孔材料流动的基本定律，它最初只是一个经验定律，后来在理论上由纳维-斯托克斯方程推导出来。它描述了速度场 \mathbf{u}(m/s)与压力梯度 p（Pa）之间的线性关系。

(1)

其中，\kappa(m²) 是多孔介质的渗透率， \mu (Pa·s) 是流体的动力黏度。

在规则结构中，如填充床或粒状土壤，渗透性可以由 Kozeny-Carman 关系推导：

(2)

其中，d_\textrm{p} (m) 表示有效粒径（对于球形颗粒，等于球体直径）。

线性达西定律适用于低速流动。与自由流动一样，多孔介质中的雷诺数

(3)

也用于表征流动，L (m) 是特征长度尺度。

线性达西定律适用于 Re<10，因此孔隙尺度流动可以被描述为蠕变流，其中惯性力与黏性力相比非常小。地下水流和其他低速和（或）高黏度流动的应用就是这种情况。然而，在大多数工业应用中，例如在填充床反应器、过滤器甚至食品工业中，都涉及到更高的流速，包括黏度非常低的气流。在这些应用中，仅使用方程1是无法描述的，还必须引入非线性项。这被称为非达西流，表述如下：

很明显我们可以看到，等式右侧的左项对应于达西定律。对于非线性项，Forchheimer 方程表明，

(4)

其中，\beta 是惯性阻力系数，c_F 是 Forchheimer（无量纲）参数。

对于填充床，Ergun 方程非常有用，可以使用以下关系式：

(5)

在高雷诺数下，与惯性效应相比，黏性效应较小，并且 Ergun 方程中的非线性项占主导地位，被称为 Burke-Plummer 方程。

这些方程对多孔介质的非线性流动具有了一定的描述性，这在图表中会更便于观察。为了更好地观察，我们以平均粒径 d_p=0.1 (mm) 的填充床中速度与压降的关系为例来说明。在下图中，Kozeny-Carman 描述了线性极限，Burke-Plummer 描述了二次极限。Ergun 和 Forchheimer 方程都可以描述线性和二次极限，两者之间的区别在于是根据方程2 还是方程5 计算渗透率。

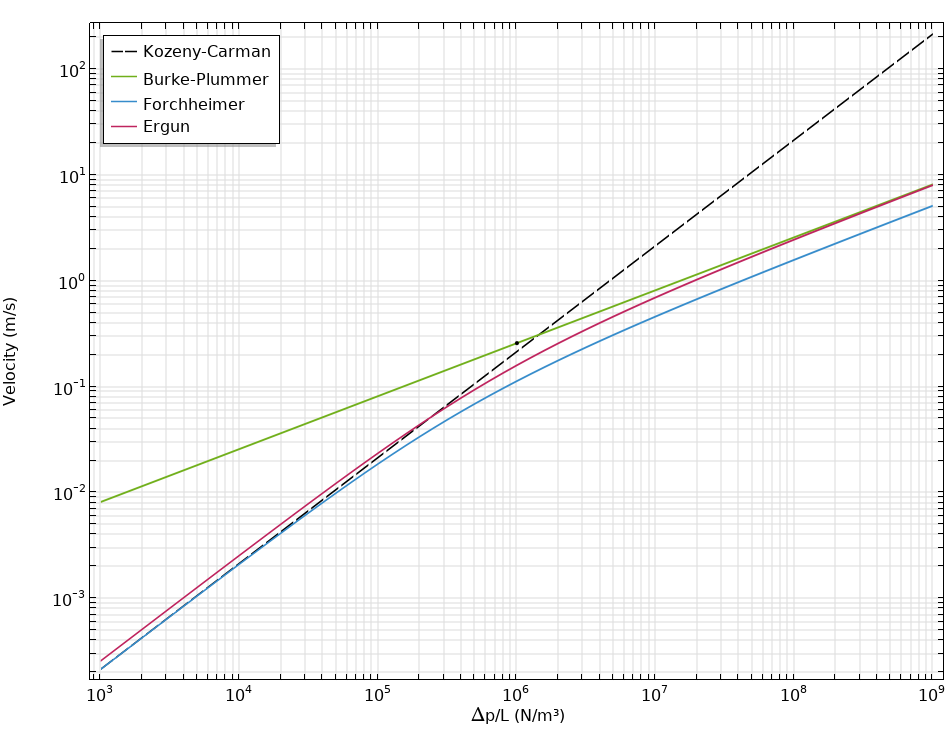
Kozeny-Carman、Forchheimer、Ergun 和 Burke-Plummer 关系的比较。

除上述考虑的情况之外，还有一种完全不同的非达西定律用于处理特殊的气体流动，即气体分子的平均自由程与孔隙尺寸大致相同的情况。在这种情况下，气体分子与孔道壁的碰撞比与其他气体分子的碰撞更频繁。这就是所谓的滑移流状态，其典型应用范围涉及从纳米材料到气体储藏建模。这种情况下的渗透率关系为

(6)

其中，p_\textrm{A}
是绝对压力 (Pa) 和 \kappa_\infty 是高压下的渗透率 (m²)，相比于分子之间的碰撞，分子与壁的碰撞与可以忽略不计。

Klinkenberg 参数 b_\textrm{K} (Pa) 取决于多孔介质的渗透率，我们可以在文献中查到 b_\textrm{K}
\propto\kappa_\infty^{-0.36}（参考文献 1）。

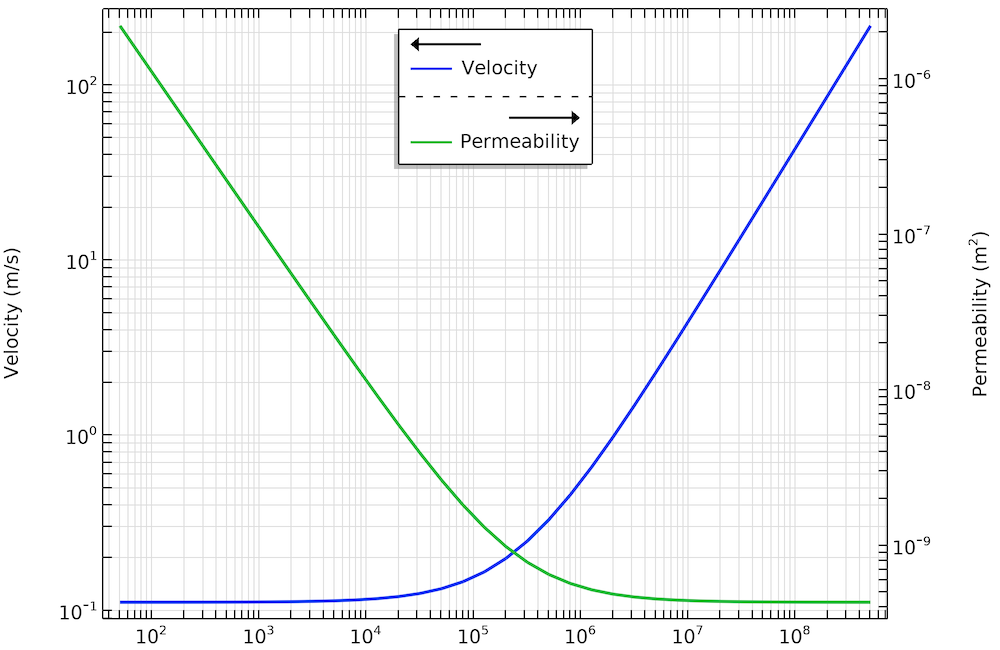
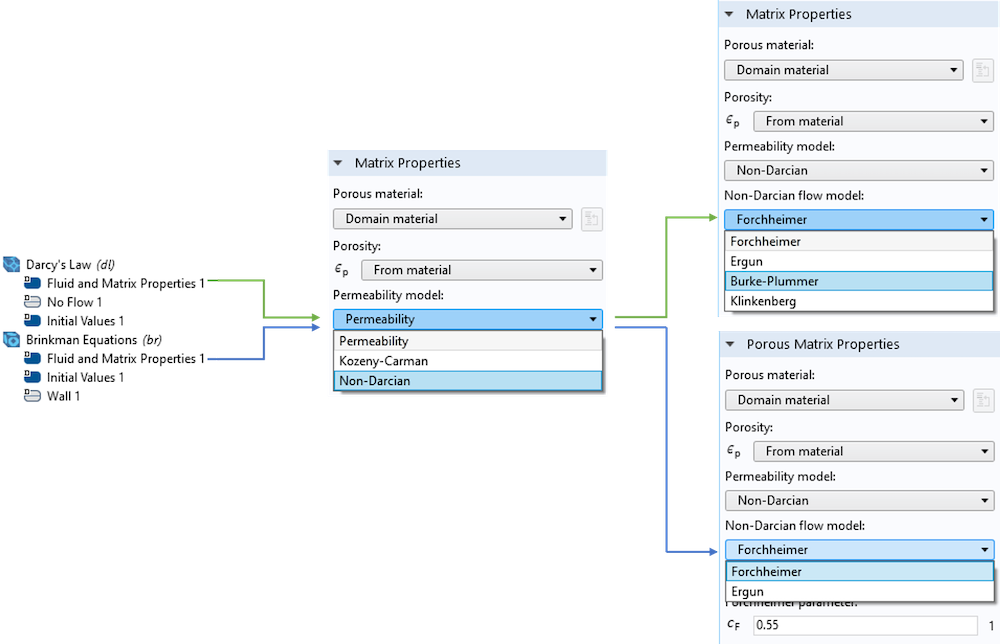
COMSOL 中的多孔介质流模块包含了所有上述渗透率模型。Forchheimer 和 Kozeny-Carman 方程也可用于支持多孔介质流动的其他模块。

软件中渗透率关系的位置。

非达西流，从微观到宏观尺度

那么，我们如何将这两种方法联系起来呢？第一个模型（REV）给出了速度对压力梯度的关系，我们还可以确定孔隙率和渗透率。类似的，我们还可以观察几个数量级的压降流动行为。由于结构复杂，孔隙结构模拟的计算成本相对较高，因此必须合理的求解。此外，与平均方程（方程2–方程 6）相比，纳维-斯托克斯方程本身就更为复杂。

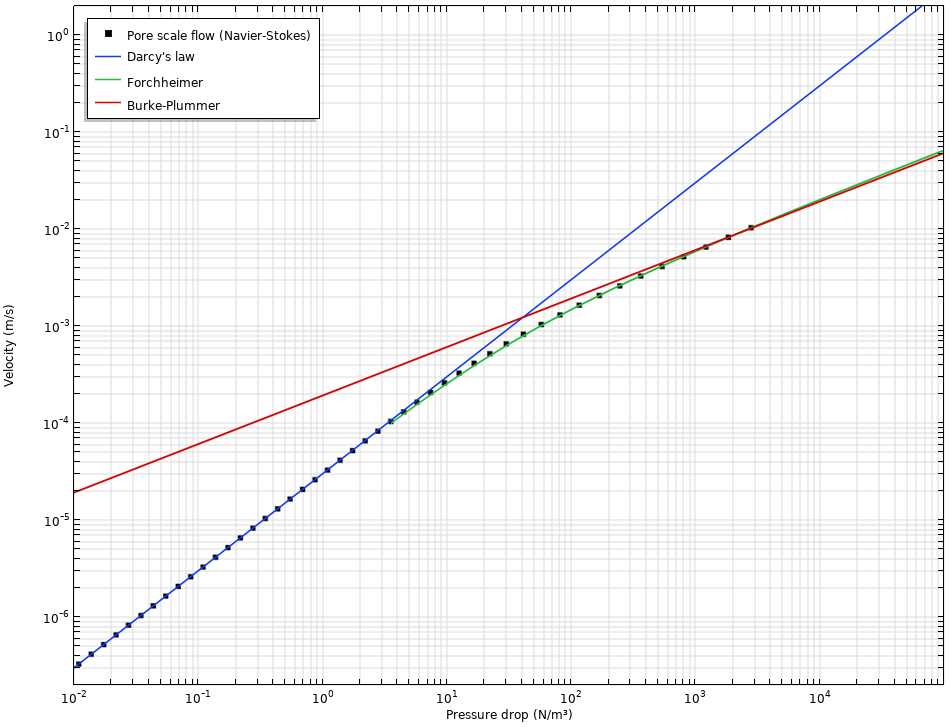
使用宏观方法可以得到非常好的近似值。达西定律适用于小压降和低速流动，而 Burke–Plummer 方程适用于大压降和高速流动。

Forchheimer 方程可以很好地计算过渡区域。在本文的示例中，将 Forchheimer 方程与来自微观模型的数据相拟合，以获得 Forchheimer 参数 c_\textrm{F}，该数据通常是在实验中确定的。

结束语

在这篇博文中，我们从微观和宏观层面研究了多孔介质中的流动，并表明了：在各自的适用领域，使用宏观方法可以得到非常好的近似值。

多孔微通道散热器的优化模型就是使用 Forchheimer 方程模拟的一个工业应用例子。

在讨论了通过多孔介质的流动之后，接下来的博文我们将讨论多孔介质中的传热，敬请期待！

动手尝试

单击下面的按钮，进入 COMSOL 案例库，您可以在其中下载 MPH 文件。尝试自己动手模拟本博客文章中介绍的教程模型。

参考文献

1. Y. Wu, K. Pruess, and P. Persoff, “Gas Flow in Porous Media With Klinkenberg Effects“, Transport in Porous Media, vol. 32, pp. 117–137, 1998.
2. J. Bear, Dynamics of Fluids in Porous Media, Courier Corporation, 1988.