电流模型中的色散仿真

随着 6.2 版本的发布，COMSOL Multiphysics^®软件模拟电色散的功能现在已经扩展到支持时域和频域仿真的电流接口。这个功能对于包括绝缘体和活体组织在内的各类材料的精确仿真尤为重要。这篇博客，我们将简单复习一下什么是色散，然后介绍如何将其纳入 COMSOL 模型，并讨论为什么这个功能很重要。

背景知识

在模拟施加到活体组织的快速脉冲电流时，例如在心脏消融、电穿孔或神经刺激等应用中，需要考虑组织以及电绝缘体的色散性。

所有材料都有电色散性，也就是说相对介电常数随激励频率的变化而变化。介电常数是一种衡量材料在电场作用下的响应或极化程度的指标。由于材料及其结构中的原子和分子不同，响应的大小随频率而变化。这也是衡量当材料暴露在时变信号下时有多少电能可转化为热能或损耗的标准。这些损耗由原子和分子在时变场中振荡时发生相对运动而产生。在频域中工作时，相对介电常数用复数表示：\epsilon_r =\epsilon_r^{‘}- i \epsilon_r^{”}，其中，实部和虚部通过Kramers–Kronig 关系确定。下图显示了两条色散曲线，分别代表绝缘材料和活体组织。第一幅图中的曲线相对简单，在较宽的频带内的特性几乎一致，因此并不总是有必要考虑色散问题。另一幅图中，总有一个频段内的特性会发生显著变化，故有必要考虑色散。

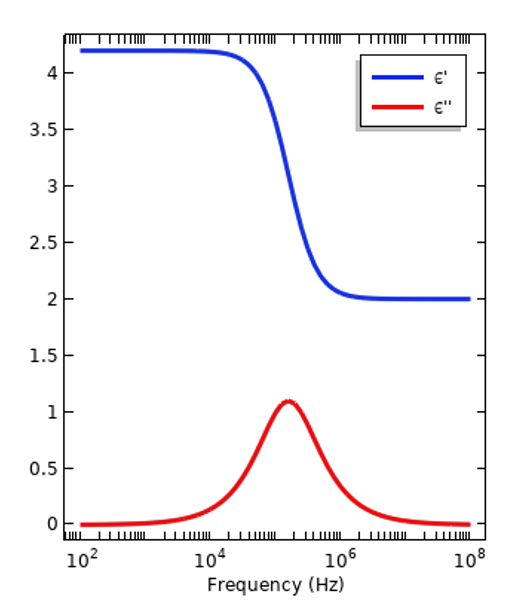
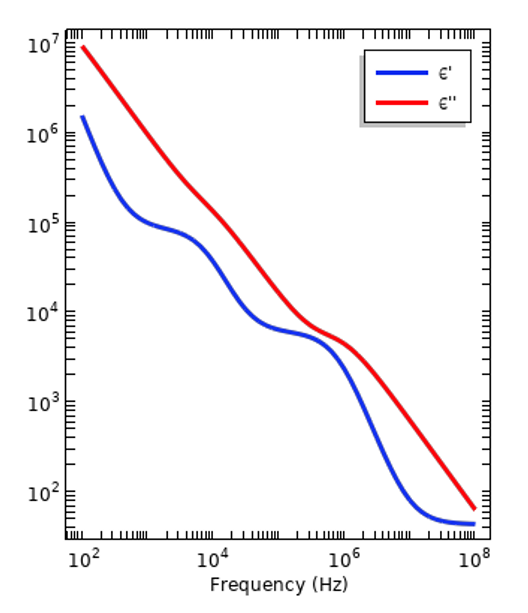
绝缘体（左）和活体组织（右）的代表性色散曲线。图中绘出了相对介电常数的实部和虚部分量的大小。

除了与频率相关的损耗之外，静态电场中也存在电损耗，这些损耗可以用直流电导率\sigma_{DC}来量化。所有材料都有一定的直流电导率，但可能非常非常小。这是一种与色散损耗不同的损耗机制。用总电导率来表示所有的材料损耗（无论其机制如何）比较方便:\sigma_{tot} =\sigma_{DC} + 2\pi f \epsilon_0\epsilon_r^{”},下图是同样两种材料的总电导率。不过，需要注意的是，与频率相关的电导率也可以不含直流分量，例如，\sigma(f) = 2\pi f \epsilon_0\epsilon_r^{”}，其中\sigma_{DC}单独绘制。

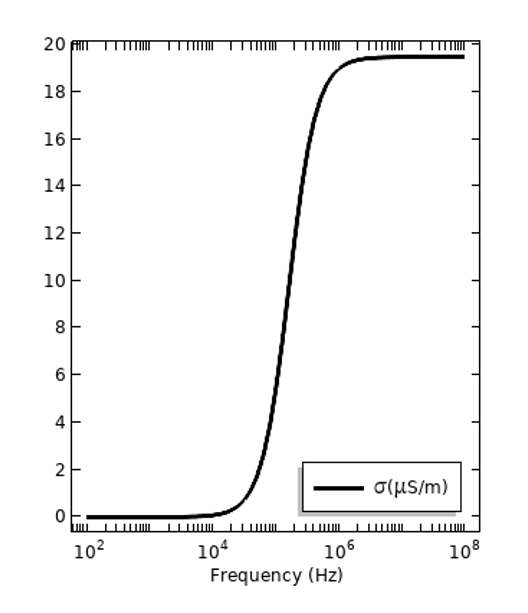
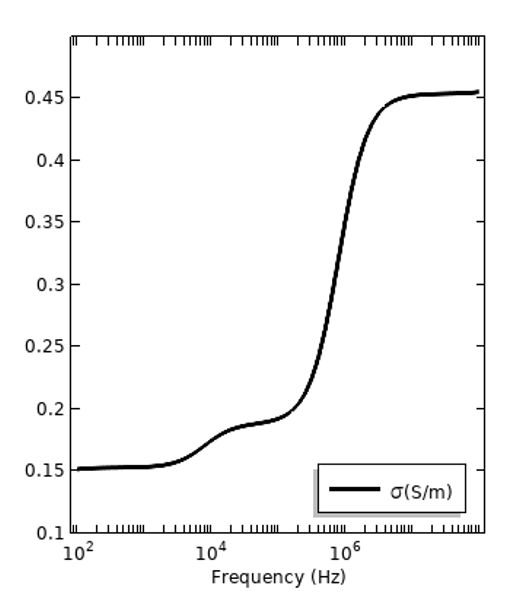
绝缘体（左）和活体组织（右）的总电导率损耗，其中包含直流电导率对色散损耗的贡献。

虽然材料特性是通过实验确定的，但我们并不想直接使用实验数据，因为这些数据会有一些不确定性，并且不满足 Kramers–Kronig 关系，从而需要非因果建模。相反，我们会将数据拟合成一个已经满足 Kramers–Kronig 关系的函数，并使用该拟合函数的系数来描述材料行为。目前，软件支持多极德拜模型，该模型将任意数量的极点N作为输入，其中每个极点m都有一个弛豫时间\tau_m和相对介电常数\Delta \epsilon_r_m，由此定义的复值介电常数为：

其中，\epsilon_\infty基于低频限制\epsilon_\infty \rightarrow \epsilon_{rS}-\Sigma \Delta \epsilon_r_m或高频限制\epsilon_\infty \rightarrow \epsilon_{rS}。此外，由于温度的变化，弛豫时间可以选择使用Vogel-Fulcher、Arrhenius、Williams-Landel-Ferry或Tool-Narayanaswamy-Moyniha转换函数中的任何一种，甚至是用户自定义的转换函数。

如果您有介电常数实部和虚部的实验数据，并希望拟合出德拜模型，则可以使用 COMSOL^®6.2 版本中的部分分式拟合功能来实现。有关该功能的使用指南，请参阅 COMSOL 学习中心的文章：根据实验数据拟合德拜色散模型。

使用电流接口

在电流模型中加入色散只需要几个步骤。首先，必须添加电流守恒域特征并将其应用在相关域。在该特征中，材料类型必须设置为固体。在假设流体不变形的情况下，这个特征也可用于流体仿真。

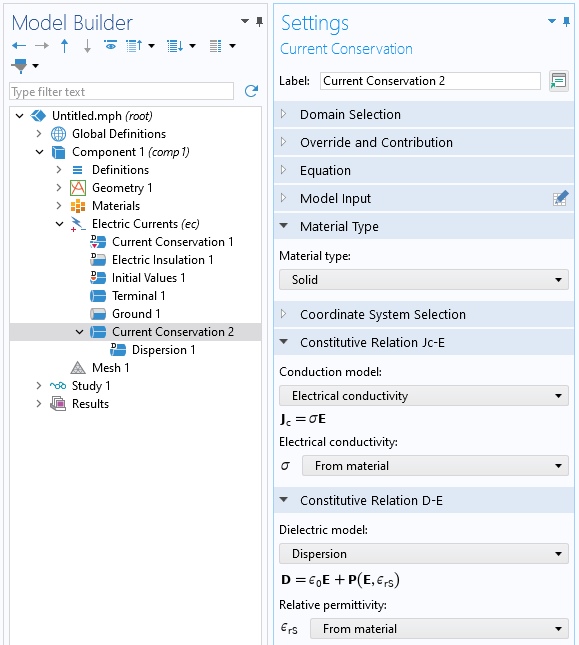
电流守恒特征，可选择色散介电模型。

将介电模型选项更改为色散后，将出现一个附加子功能。在该功能中，可以输入多极德拜模型的分支以及限制行为，如下图所示。除了输入极点或分支外，还可以通过恒定损耗角正切模型指定弛豫数据，该模型将损耗角正切、中心频率和带宽作为输入。根据这些输入，软件会自动确定极点数、弛豫时间和相对介电常数。也可以使用更简单的德拜模型，该模型只有一个极点。通过热效应设置可以选择启用导致弛豫时间转换的热效应。

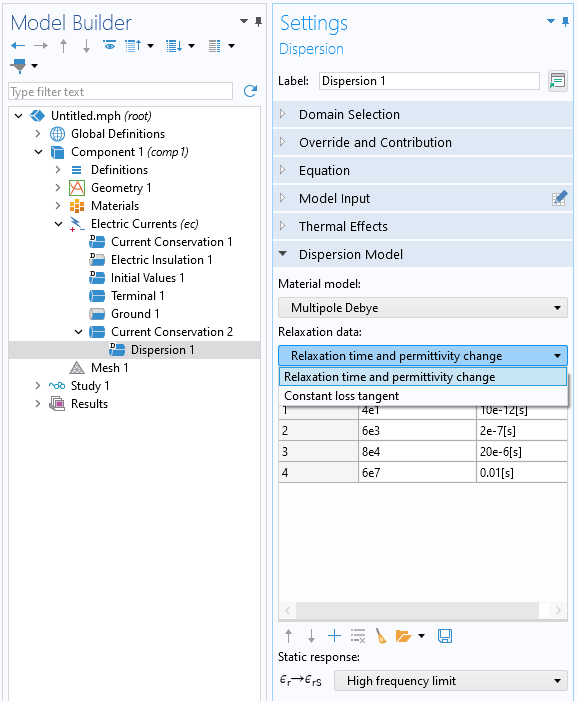
输入多极德拜模型的分支和指定限制行为的色散子特征。

查看结果

我们可以研究色散如何影响一个简单系统的响应，例如在频域中工作的平行板电容器案例模型所示，也可以尝试将两种不同的材料夹在其中。由下图我们可以看到阻抗的实部和虚部是如何随频率变化的。

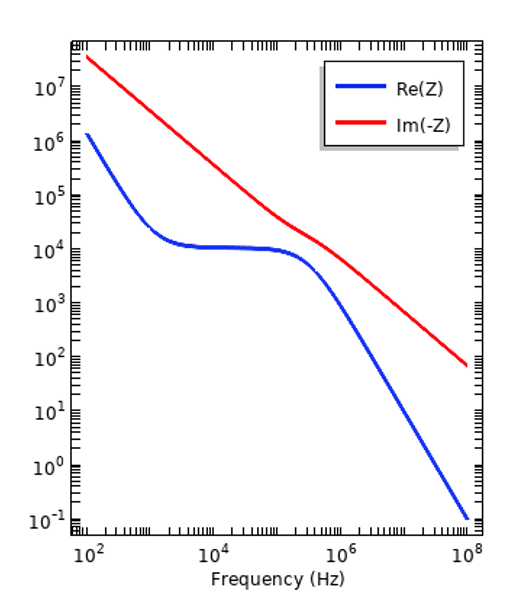
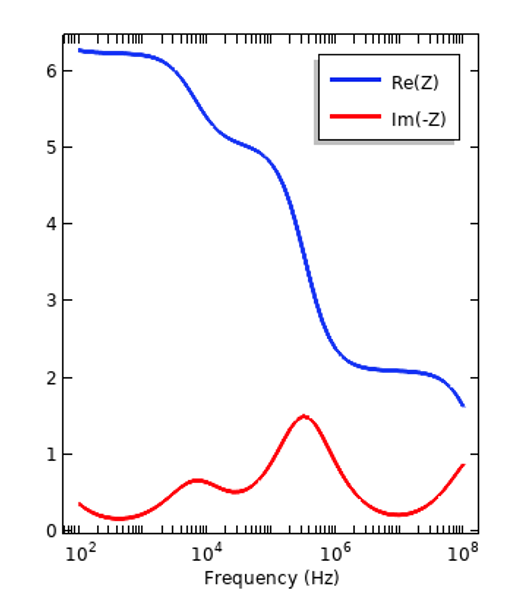
内含绝缘体（左）和活体组织（右）样本的平行板电容器的阻抗。请注意，绘制的是阻抗的负虚部分量。

我们还可以使用相同的模型来查看同一系统中的时域激励结果。我们只研究样本组织材料，因为其响应随频率的变化更为显著。色散材料的设置是相同的，但建议您复习一下这篇博客：激励这种系统的各种方法。我们首先用在 10ns 内从 0 A递增到 1A 的平滑外加电流来激励系统，然后通过绘制终端感应电压图计算 100µs 内的响应（见下图）。结果随时间变化，并以对数标尺绘图。

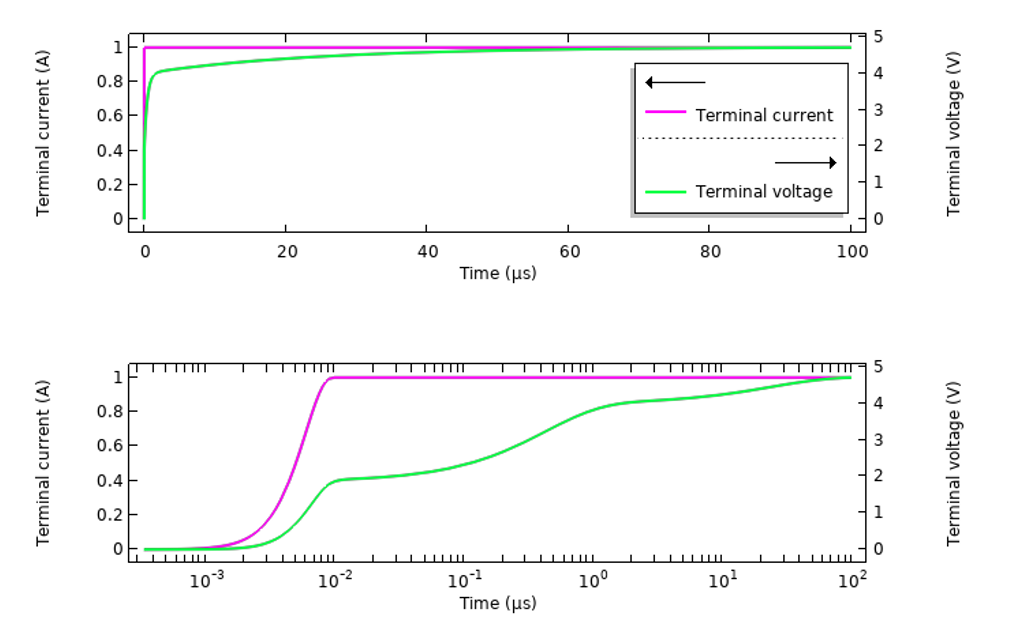
活体组织样本材料对外加电流的瞬时响应。

将这些结果与通过沿传输线传输的类似平滑递增电压信号激励的模型进行比较非常有意思。下图显示了测量的电流和电压的响应。请注意，这里绘制的电压信号是入射的平滑递增电压信号与来自结构和材料的反射信号之和。由于材料的色散作用，总信号表现出时变特性。

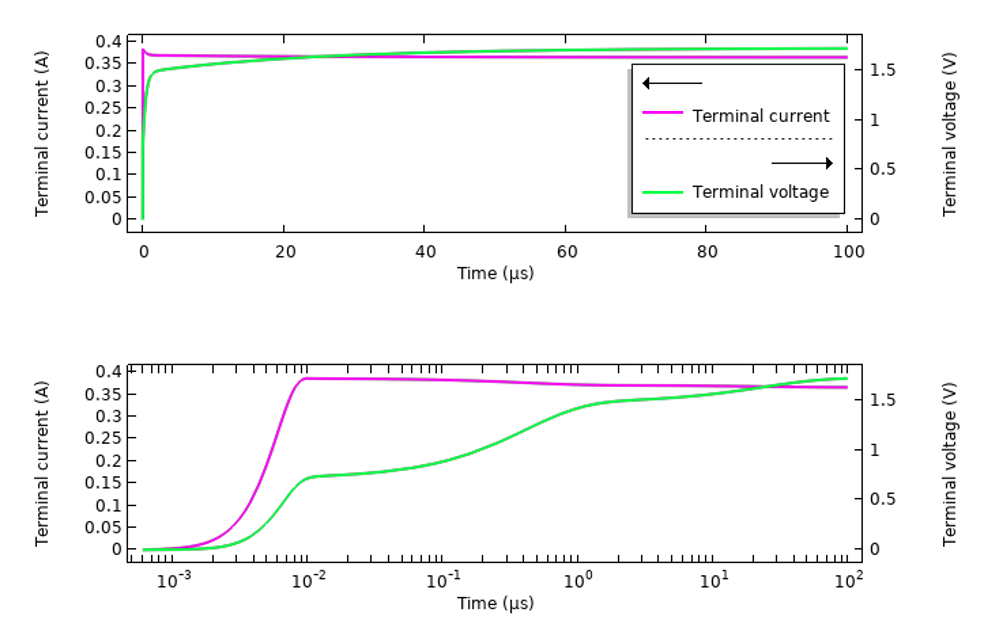
由传输线激励的活体组织样本材料在递增电压信号下的瞬态响应。

结束语

现在，我们可以在电流接口中建立电色散模型，而且设置非常简单。这种材料模型可以更准确地反映真实的电响应，以及频域和时域模型中的损耗。这个功能对许多材料的仿真都非常有用。

请注意，通过静电接口也可以模拟电色散，而且从 6.0 版本开始就可以实现，该接口主要用于有损压电材料的建模与仿真。此外，如果要模拟更高的频率，RF 模块和波光学模块中还包括其他色散模型。