
想象一个场景:来回弯曲一个金属回形针,重复多次直到它完全断裂。这就是一个疲劳失效的例子,也是最常见的结构坍塌类型。在更严重的情况下,这种失效可能会导致汽车排气管和飞机喷气发动机等结构坍塌或失效。为了更好地了解和预测弹塑性材料的疲劳失效,我们可以使用 COMSOL Multiphysics®软件对材料和疲劳过程进行精确模拟。
什么是弹塑性材料?
弹塑性材料兼具两种主要行为类型:弹性变形(可逆变形) 和塑性变形(或塑性),后者不可逆并在卸除载荷后会留下永久变形。为了模拟这种类型的材料行为,我们需要使用一种本构关系,既不仅能将应力状态与当前应变状态联系起来,还能将之前积累的塑性应变及其发展联系起来。

承受内部压力的压力容器的塑性变形,显示了弹性区域(深蓝色)和塑性区域(红色)。
一般来说,当应力增加并超过初始屈服应力(弹性极限)时,弹塑性材料的应变比弹性区域中相应应力增加时的应变要大得多。材料通过塑性变形而硬化,但不同材料在塑性状态下的响应差异很大。
对于金属材料,硬化通常由三种不同类型的行为来描述:
- 各向同性硬化,该情况下,屈服面随着应力的增加而扩大。拉伸中的载荷也会使压缩材料硬化
- 运动硬化,该情况下,屈服面平移,尺寸不变。拉伸中的载荷将使材料在压缩时变得更软
- 混合硬化,该情况下,屈服面会扩大和平移
在下图中,我们可以直观地看到三种硬化类型在单轴载荷下的应力-应变关系。第一步,材料被拉伸,直到达到显著塑性应变。此时,当前的屈服应力\sigma_{\textrm{y}}高于初始屈服应力\sigma_{\textrm{y0}}。至止,三种硬化类型的应力-应变曲线遵循相同的路径。第二步,反向施加载荷,压缩材料直到压缩屈服开始。
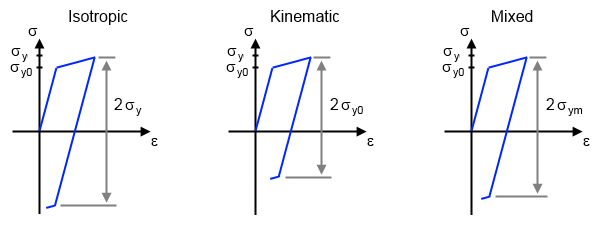
三种硬化模型(各向同性模型、运动模型和混合模型)在单轴荷载工况下的应力-应变关系。
对于各向同性硬化,材料可以在反向屈服开始之前最多被压缩2\sigma_{\textrm{y}}。对于运动硬化,材料最多可以被压缩2\sigma_{\textrm{y0}}。对于混合硬化,压缩量介于两者之间,为2\sigma_{\textrm{y0}} < 2\sigma_{\textrm{ym}} < 2\sigma_{\textrm{y}}。运动和混合硬化都会导致所谓的反向应力或转移应力,这是一种新的应力水平,在拉伸和压缩过程中都远远没有屈服。在塑性开始之前以及各向同性硬化的情况下,反向应力为零。
除了这种类型的变形硬化外,一些金属材料还表现出更复杂的行为类型。例如塑性行为取决于应变率的黏塑性材料。
在 COMSOL Multiphysics®中模拟疲劳失效
您可以访问非线性结构材料模块中可用于模拟弹塑性材料的材料模型集。不过,选择一个疲劳模型不仅取决于材料模型,还取决于载荷特性。在上一篇博客中,我们讨论了载荷条件对疲劳模型选择的影响。
在使用像弹塑性材料这样的非线性材料时,第一个载荷循环的材料响应通常与第二个循环的材料响应不同。这是由既可以移动屈服面也可以改变屈服应力的第一个载荷循环引起。然后,连续的载荷循环可以在新的应力-应变状态附近振荡,或者导致非弹性应变进一步积累。在研究疲劳时,首先要找到一个代表后续循环的稳定的载荷循环。因此,在模拟弹塑性材料时,通常需要模拟几个载荷循环才能达到稳定的载荷循环。
在博客:非线性材料中的热疲劳仿真中,我们讨论了不同类型的载荷循环。
接下里,我们来看看如何在 COMSOL Multiphysics 中使用两种硬化类型(运动硬化和各向同性硬化)来模拟弹塑性材料中的疲劳。
使用运动硬化模拟材料中的疲劳
我们以带孔气缸的弹塑性低周疲劳分析案例模型为例。在这个案例中,部件的载荷超过了屈服点,因此材料立即变得稳定,因为在第二个循环中已经获得了稳定的载荷循环。不过,稳定的载荷循环包括弹性和塑性变形。这是可能的,因为材料是使用运动硬化模拟的。这意味着屈服面在两个位置之间移动:拉伸和压缩。
对于大多数涉及运动硬化的应用,必须进行完整的弹塑性分析。通过将模型划分为塑性延伸域和仅发生弹性变形的域,可以在一定程度上减小模型大小。这种方法很有用,因为塑性模拟的计算成本很高,需要我们评估额外七个自由度,而弹性材料只有三个位移。
疲劳失效通常是因为存在一个缺口。在这种情况下,可以使用近似解;例如,基于 Ramberg-Osgood 材料模型的塑性 Neuber 校正。在弹性解的基础上,该近似方法能够计算缺口处的弹塑性应力-应变状态。这种方法计算速度很快,但是离缺口越远,结果的准确性就越低。我们在一个相关的案例模型中对该方法进行了演示:带孔气缸的缺口近似低周疲劳分析。
我们可以通过下图比较这两种方法。由于孔的高应变和多轴载荷条件,我们使用 Smith-Watson-Topper(SWT)模型预测疲劳。两种方法在临界点的计算结果相似,但计算时间差异很大。弹塑性模型的计算时间为几分钟,而缺口近似法的计算时间为几秒钟。
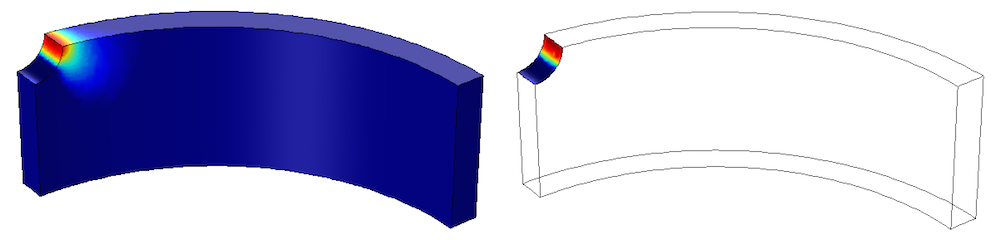
使用完整弹塑性分析(左)和缺口近似分析(右)的低周疲劳预测。计算结果显示疲劳周期数的对数。两幅图中使用了相同的色标。
使用各向同性硬化模拟材料中的疲劳
在另一个案例模型:长期接触疲劳中,表面硬化材料承受压缩载荷循环。受硬化过程的影响,被测材料有三个具有不同材料特性的层。最靠近表面(外壳)的材料很坚固,而内部深处(内芯)很脆弱。在这两层之间,有一个材料特性和残余应力都急剧变化的薄过渡层。
不同深度的材料塑性性能有所不同。在表层,硬化遵循线性各向同性模型,而在内芯,硬化遵循指数硬化模型。在过渡层,硬化函数遵循指数硬化模型,并已经参数化。选择材料参数的函数,以使过渡层交界处的材料模型与表层模型相对应,内芯交界处的材料模型与内芯模型相对应。
在第一个载荷循环中,材料被压缩超过屈服点,塑性在过渡层增长。由于屈服面在各向同性硬化过程中扩大,如果每个连续的载荷循环的大小不如第一个循环高,就不会进一步产生塑性,因此稳定的载荷循环是弹性的。尽管在第一个载荷循环中会产生高应变,但任何连续的循环都会导致较小的应变变化。因此,可以合理地假设由应力驱动的高周疲劳模型适用于疲劳评估。
在以压缩载荷为主的情况下,Dang Van 模型非常适用于疲劳建模,因为它考虑了压缩平均应力。您可以在疲劳模块中访问用于这类模拟的 Dang Van 模型。
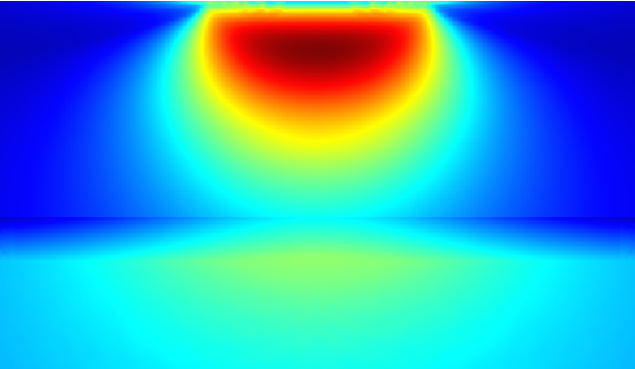
表面硬化材料的疲劳预测。显示了疲劳使用因子。疲劳风险最高的是近表层,疲劳风险较低的是深层内芯。
通过使用 COMSOL Multiphysics 模拟常见类型的弹塑性材料的疲劳,可以更好地了解和预测疲劳失效的发生。



评论 (0)