在高频电磁学中模拟石墨烯材料

石墨烯等二维材料具有良好的性能，因此成为研究和应用的热点。在这篇博客中，我们将以石墨烯基太赫兹超材料完美吸收体为例，演示如何在高频电磁学中精确、高效地对二维材料进行建模。本文所讨论的技术同样适用于其他薄层的模拟，例如光学器件上的涂层。

简介

石墨烯是一种仅由单层碳原子组成的材料，这些碳原子以六边形晶格的形式排列。长期以来，物理学家一直假设存在一种具有单个原子层的材料。几十年前，人们普遍认为，由于热力学不稳定性，像石墨烯这样的材料不可能在自然界中存在。2004年，由曼彻斯特大学的 Konstantin Novoselov 和 Andre Geim领导的一个物理学家团队首次通过实验证明了石墨烯的存在。这一发现被认为是非常重要并具有革命性，因此很快在 2010 年获得了诺贝尔奖。

当前，这种材料已经被全球的物理学、材料学等领域科学家和工程师广泛研究。此外，越来越多的单层材料，如六方氮化硼、黑磷、二硫化钨等，多年来相继被发现。如今，对包含二维材料器件的需求持续上升，因此需要对这些材料进行多物理场建模。

在此，我们将讨论在高频电磁场中对石墨烯等非常薄的材料建模的不同方法。如果你对包含二维材料或其他薄层的光电或光子器件的模拟感兴趣，应该会从以下讨论中受益。

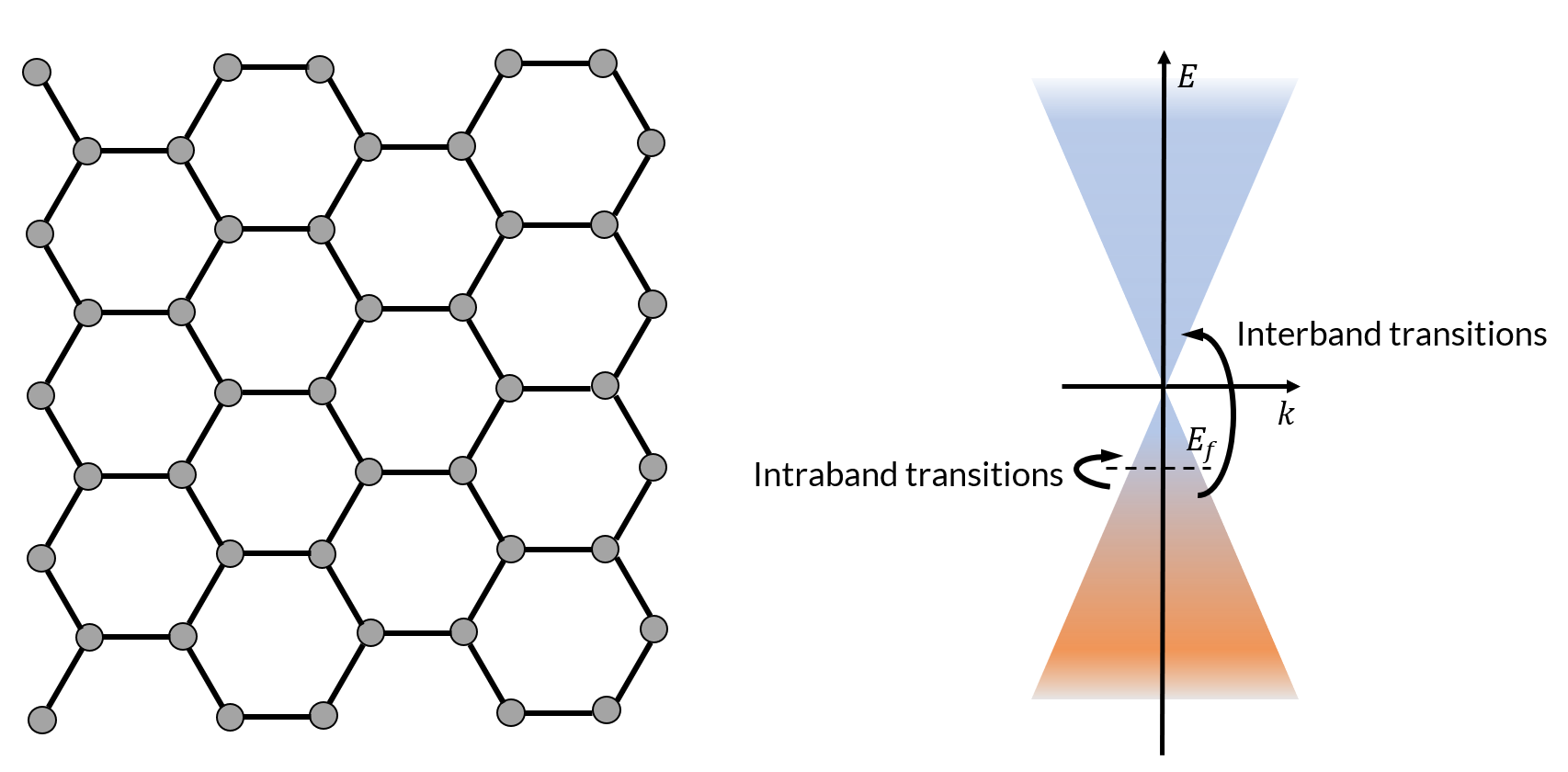
左图显示了石墨烯的六边形晶格结构，其中灰色圆圈代表碳原子。右图显示了石墨烯中的线性能量–动量色散关系，通常被称为狄拉克锥。带内和带间电子跃迁都对石墨烯的导电性有贡献。

石墨烯的光学电导率

由于线性能量-动量色散，石墨烯中的电子表现得好像没有质量，这使其具有非常独特的光学和电子特性。石墨烯层的电磁特性可以通过其二维表面电导率来表征。带内和带间电子跃迁都对总电导率有贡献，即\sigma_{2D} = \sigma_{2D}^{intra} + \sigma_{2D}^{inter}。使用 Kubo 公式，带内跃迁贡献由下式给出

其中，k_B是玻尔兹曼常数，\hbar是简化的普朗克常数，T是温度，e是电子电荷，E_f是费米能量，\omega=2\pi f是角频率。这种贡献在光子能量较低（射频、微波和太赫兹范围）时占主导地位。当光子能量增加到红外和光学频率时，电子带间跃迁开始。带间电导率由下式给出

函数可以写为H

COMSOL Multiphysics^®软件内置众多物理常数，例如k_B，\hbar和e。这些常数可以写为k_B_const、hbar_const和e_const。此外，当在一个方程中使用不同单位系统中的不同量时，在 COMSOL 中也可以很方便地进行单位自动转换。带间电导率的积分可以使用 COMSOL^®中的内置积分算子计算。请注意，积分的上限是无穷大。在数值上，我们必须把它截断为一个有限值。在该模型中，数值取10^{16}rad/s 时结果趋于稳定。

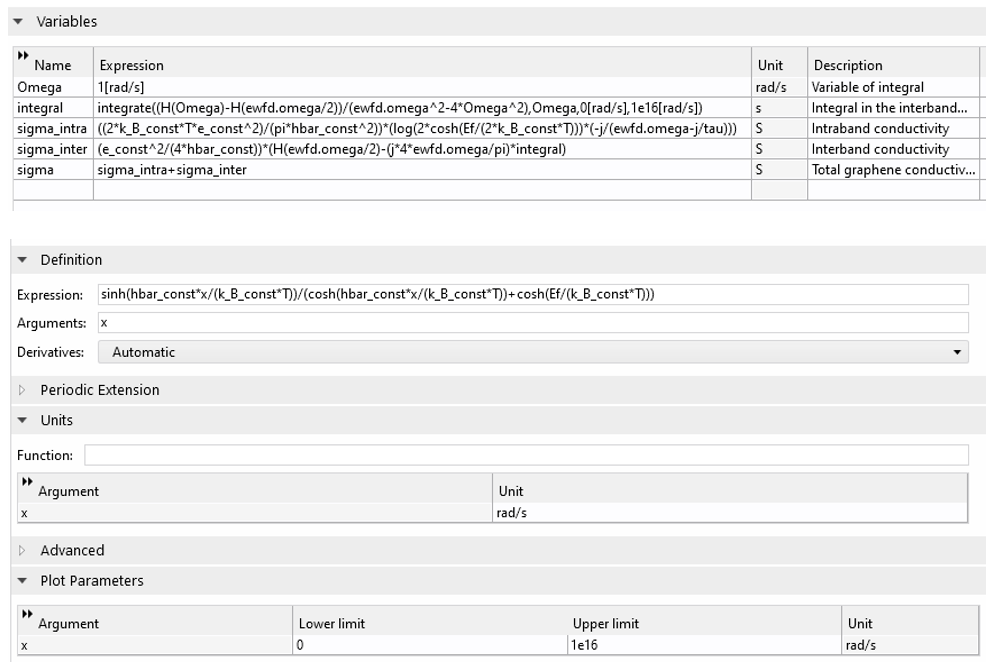
用于计算石墨烯电导率的变量和解析函数。内置常量和算子的使用大大简化了实现。

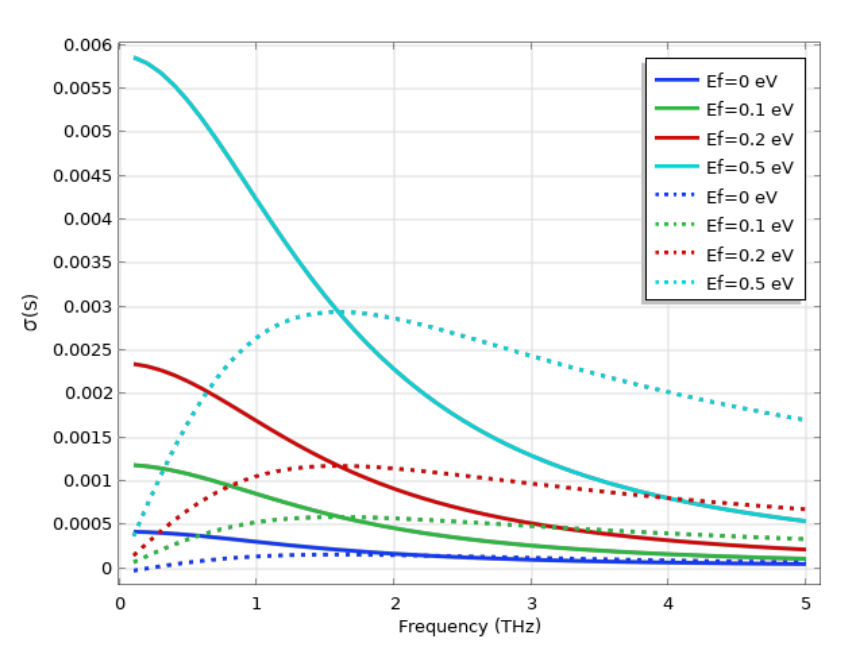
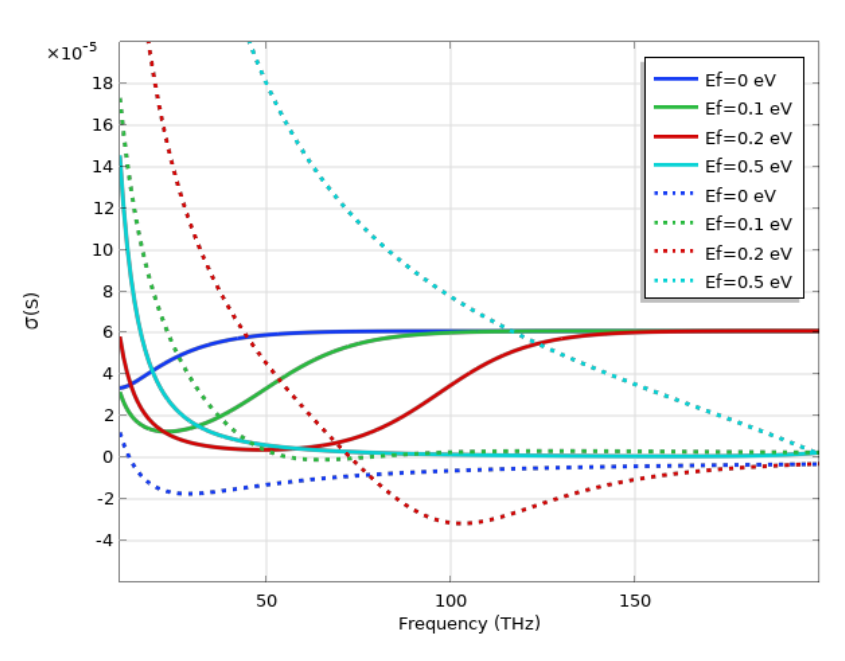
下图显示了在低频 (THz) 和高频 (IR) 下不同费米能量的石墨烯表面电导率计算结果。在低频下，带内跃迁占主导，电导率遵循类-Drude响应。在非常高的频率下，电导率接近普遍值\sigma_0=\frac{\pi e^2} {2h}\approx 6 \times 10^{-5} S，h是普朗克常数。在这里，我们还可以通过电调控或化学掺杂改变费米能量，可以看到石墨烯出色的可调性。这使得石墨烯成为电子和光电器件中非常理想的材料。最后，如果我们想将石墨烯视为三维平板，则可以由二维表面电导率计算出三维电导率\sigma_{3D} = \sigma_{2D}/d，d是石墨烯的（有效）厚度。

左图显示了在太赫兹频率范围内具有不同费米能量值的石墨烯电导率，其中带内跃迁是主要效应。右图显示了在红外频率范围内具有不同费米能量值的石墨烯电导率，其中带间跃迁的贡献变得很重要。在这两个图中，实线代表电导率的实部，虚线代表电导率的虚部。

在射频和波动光学模块中对石墨烯进行建模

那么，我们应该如何在电磁仿真中模拟石墨烯呢？由于其原子厚度，将它明确建模为实际厚度约为 0.34 nm 的三维薄板，计算量很大，而且很可能是不必要的。接下来，我们将演示三种不同的方法：分别使用过渡边界条件、表面电流密度边界条件和一个有效厚度的三维板。我们发现，就远场光谱而言，这三种方法都能得到几乎相同的结果。请注意，这里所讨论的技术是通用的。它们不仅适用于石墨烯，而且适用于任何几何薄层。作为一个具体的例子，我们将构建一个参考文献1中提出的基于石墨烯的太赫兹超材料吸收器。

在下图所示的吸收器结构中，由两个石墨烯层制成的网状图案被嵌入聚合物介质中。结构底部的金属接地层用作反射面。地平面和石墨烯之间有效地形成了一个 Fabry–Perot 谐振器。我们很容易注意到，单元格中有两个镜像对称。因此，可以使用 COMSOL 中的完美电导体和完美磁导体边界条件来描述这些对称平面，因此只需对四分之一的单元格进行建模。当我们考虑太赫兹辐射的法向入射时，这是适用的，在这个示例模型中就是这种情况。

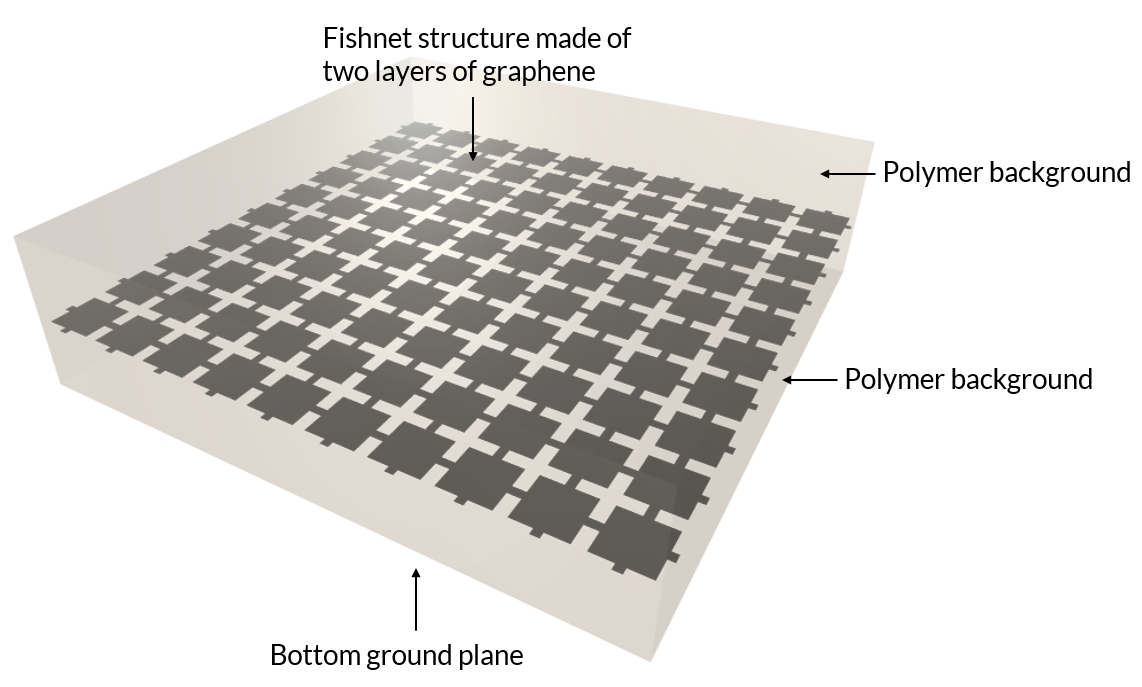
基于石墨烯的太赫兹超材料吸收器，由石墨烯层制成的网装结构被嵌入聚合物介质中。模型的底部是金属接地层。

在 COMSOL 软件的RF 模块和波动光学模块中，内置的过渡边界条件可用于模拟内部边界上的几何薄层。在物理上，它表示由于感应表面电流密度导致的切向电场的不连续性

和

其中，Z_S = -\frac{j\omega\mu}{k}\frac{1}{tan(kd)}，Z_T = -\frac{j\omega\mu}{k}\frac{1}{sin(kd)}和k=\omega\sqrt{\mu(\varepsilon+\frac{\sigma}{j\omega})}。指数 1 和 2 指的是表面的两侧。默认情况下，过渡边界条件假设薄层中的正常传播，这在我们的模型中得到满足，同时仍然假设层具有有限的厚度。石墨烯的（有效）厚度d可以设置为任意小的值，例如 1 nm，只要将三维电导率相应地缩放为\sigma_{3D}= \sigma_{2D}/d。由于在这个特定模型中有两层石墨烯，我们将在过渡边界条件设置中输入厚度2d（详情请见相关模型，链接在本文的末尾）时，三维电导率计算为\sigma_{3D} = \sigma_{2D}/d。（有关详细信息，请参阅本博文末尾链接的相关模型）。请注意，两个单独的石墨烯层紧密放置在一起，与双层石墨烯之间存在明显差异。当两个单独的石墨烯层紧密地放置在一起时（如该模型），每一层的电导率都不会改变。另一方面，双层石墨烯是由范德华力限制的两个石墨烯层。这种边界可以明显改变石墨烯的性质，有多个影响因素，例如堆叠顺序、扭转角度等。也就是说，在对双层石墨烯或三层石墨烯进行建模时，需要以不同的方式计算电导率。

我们模拟的器件在不同费米能量下的模拟吸收光谱如下图所示。结果与参考文献1一致。在 0.5 eV 费米能量下，存在宽吸收带，在 2.8 THz 附近获得完美吸收。高吸收是由石墨烯和底部接地平面之间形成的 Fabry–Perot 谐振器引起的。当满足共振条件时，在石墨烯中获得高吸收。该器件的吸收可以主动调整，例如通过调整石墨烯上的栅极电压。

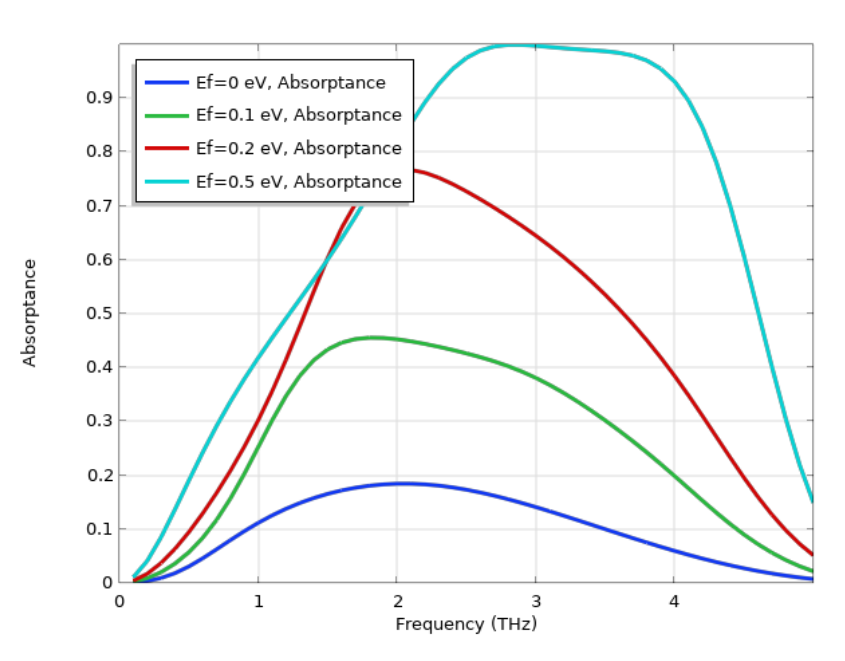
石墨烯基超材料在各种费米能量下的吸收光谱。使用过渡边界条件对石墨烯进行建模。

作为使用过渡边界条件的替代方案，我们可以使用表面电流密度边界条件直接对石墨烯进行建模，如上一篇博文中所简要讨论的那样。这样，我们可以真正将石墨烯视为没有任何厚度的二维层。这里，x和y方向上的电流密度分别设置为J_x=\sigma_{2D}E_x和J_y=\sigma_{2D}E_y的吸收光谱与过渡边界条件示例的结果相同，如下图所示。

前面讨论的侧重点是通过特定边界条件对石墨烯进行建模，避免对石墨烯层进行全尺寸三维建模。这样，模拟速度和 RAM 使用率都大大提高了。原则上，我们也可以对石墨烯进行三维建模。为了使模型尽可能逼真，一种选择是将石墨烯创建为厚度为 0.34 nm 的三维平板。然而，在这个特定模型中，我们关注的是太赫兹辐射，其波长约为 100 μm。只要石墨烯的厚度远小于波长，就其光学响应而言，没有实际差异。同样，假设三维电导率与有效厚度适当缩放。为方便演示，我们在模拟中使用了 100 nm 的有效厚度（结果可以在下面的散点图中看到）。我们可以看到，即使我们使用了比例放大的厚度，结果仍然与正确的值基本相同。选择一个较大有效厚度是合理的，因为它有助于网格剖分并避免过度网格奇异。但是对 CPU 时间和 RAM 的要求仍然比之前的方法要大得多。

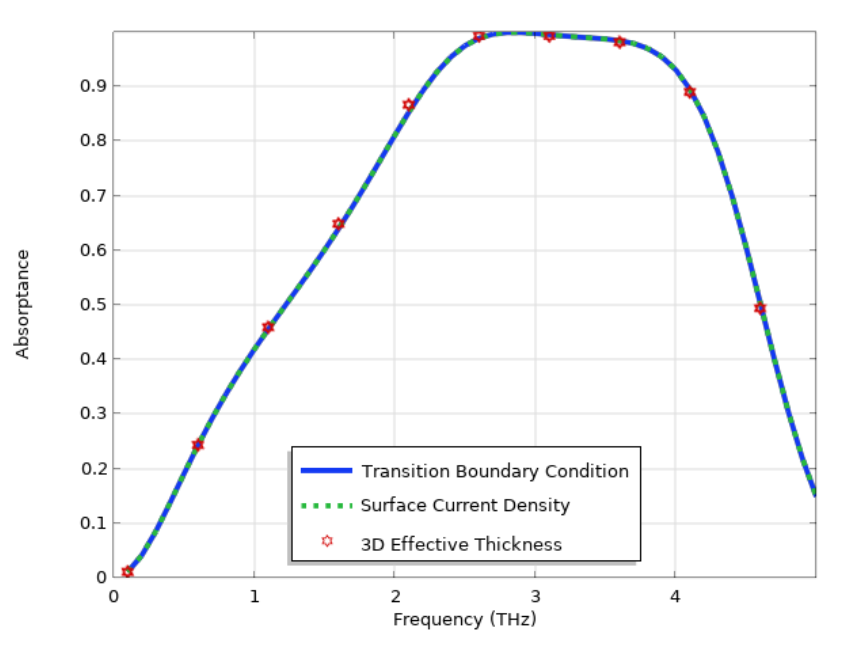
使用三种不同方法：过渡边界条件、表面电流密度和具有有效厚度的三维体积，模拟石墨烯基超材料的吸收光谱。结果基本一致，三维体积需要更长的模拟时间。

结语

总之，几何薄层在电磁建模中无处不在。除了二维材料，常见的薄层还包括光学元件上的抗反射涂层、电子元件上的导电涂层、PCB 上的薄金属层等。COMSOL 软件的 RF 模块和波动光学模块内置了过渡边界条件和表面电流密度等功能，可以帮助降低几何薄层建模时的计算复杂性。适当使用这些功能可以大大加快仿真速度，同时确保准确性。

下一步

单击下面的按钮，进入 COMSOL 案例库下载教程模型，动手尝试自己建立石墨烯超材料完美吸收器模型。

参考文献

1. A. Andryieuski and A. V. Lavrinenko, “Graphene metamaterials based tunable terahertz absorber: effective surface conductivity approach”,Opt. Express, vol. 21, pp. 9144–9155, 2013.