
在之前的一篇博客文章中,我们研究了计算和控制充满不可压缩流体的腔体的体积,其中求解了充满流体的橡胶密封件的静态变形。 在那个例子中,假设流体是不可压缩的,我们没有显式地为流体建模,而是添加了一个方程来求解压力。在这篇博客中,我们将扩展这种方法并使之包括可变形容器中流体的静水压力。
挤压水气球
考虑一个装满水的橡胶气球,放在一个开着洞的表面上,同时被压头从顶部推动。气球的变形是由于流体的重量以及压头从顶部向下推动造成的,如下图所示。我们采用超弹性材料模型对橡胶材料进行建模,并将使用在前一篇文章中介绍的技巧,在腔体变形时保持腔体的体积不变。
流体的重量使气球发生变形,这导致气球向外膨胀并陷入凹陷中;来自上方的压缩也会使它产生变形,这导致其向外和向上膨胀。由于这种压缩,气球内流体的深度会发生变化。我们想要求解这种深度变化,而不必求解流体流动的Navier-Stokes 方程,因为我们只对静态(非时变)解感兴趣。
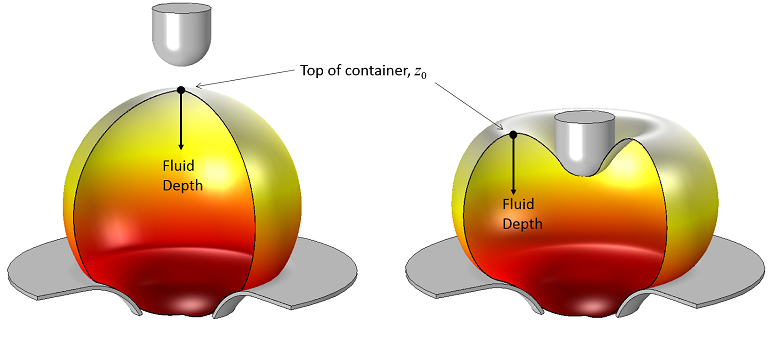
一个装满水的橡胶气球的中心被压缩。当气球被挤压时,最高点的位置和流体的深度会发生变化,从而改变静水压力分布。
合并静水压力
一个装有流体的容器会对容器壁施加静水压力:
其中,\rho是流体的密度,g是重力,z_0是容器顶部的位置,p_0是容器顶部流体的压力。由于气球中充满了不可压缩的流体,当我们用压头挤压它时,压力p_0,将会增加。
我们还可以从上面的图像中看到,随着气球被压缩,流体的深度也会发生变化。此外,似乎计算深度需要知道容器的顶部和底部的位置。那么,我们如何在深度上融入这种变化呢?接下来,让我们来看看怎么操作……
如下图所示,气球内部施加的压力载荷有两个分量。压力载荷的第一部分是根据全局方程计算的。压力载荷的第二部分是由静水压力引起的。理想情况下,第二部分的压力载荷将基于流体的深度,但这个深度是一个我们不知道的变量。所以,我们输入一个只基于z位置的静水载荷,它可以有一个任意的零水平。
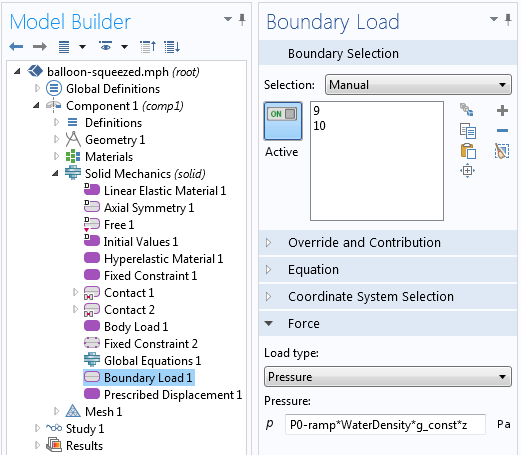
施加在气球内边界上的压力载荷是由全局方程计算出的压力载荷和静水压力之和。流体静压在求解过程中逐渐升高。
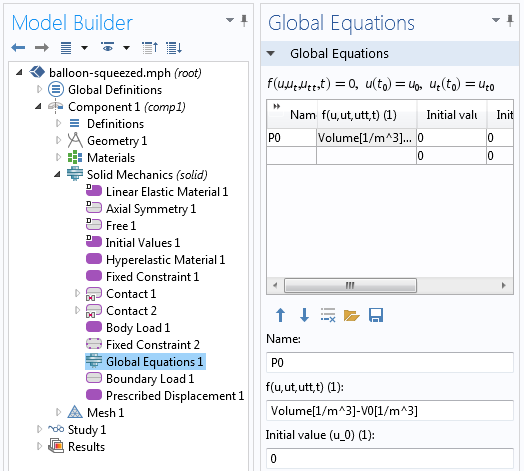
全局方程约束体积在变形过程中保持不变。
因此,这里看起来好像我们施加了一个压力载荷来约束体积和一个与 z 位置成正比的载荷,但是我们没有正确地计算静水压力,因为我们不知道z_0. 然而,事实证明,全局方程的作用可能比你最初预期的要多一些。
为了理解这一点,我们稍微重写了一下气球内部压力的方程:
我们马上就可以看到,这几乎与我们输入的压力载荷方程p(z)= P_0-\rho g z完全匹配,除此之外可以看到,我们通过全局方程计算的压力是容器顶部的压力加上未知的顶部 z 位置的偏移量。所以,虽然我们只求解一个额外的变量P_0,但它解释了两种物理效应:由于体积约束引起的压力变化以及流体顶部 z 位置的变化。
由于这个模型包含几何和材料非线性以及由于接触引起的非线性,因此收敛到解可能很困难。为了解决这个问题,我们将使用负载递增来缓慢增加重力对模型的影响,并逐渐挤压气球。二维轴对称模型用来研究结构的对称性。
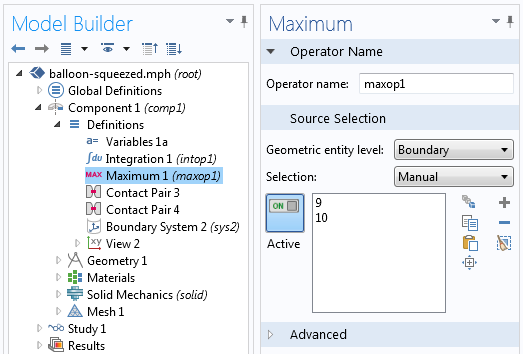
求解模型后,利用最大耦合算子对静压的大小进行后处理,计算沿气球内边界的最大z位置。
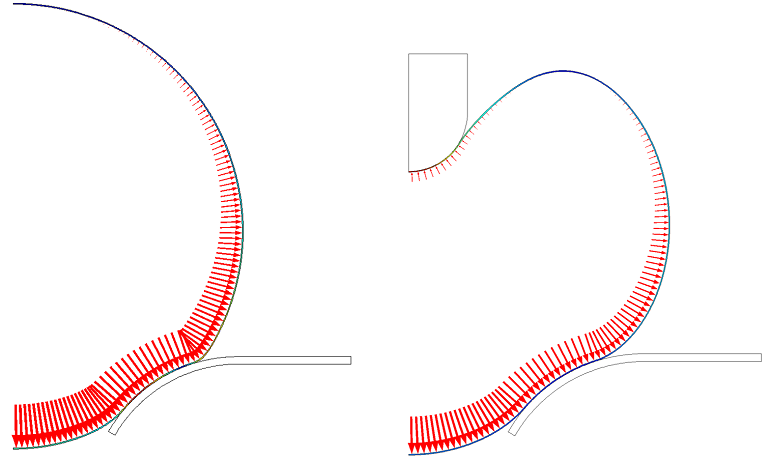
箭头表示随深度变化的静水压力载荷的解。
上图显示了气球内部的静水压力负荷。箭头的长度由以下表达式给出: WaterDensity*g_const*(maxop1(z)-z),其中 maxop1(z) 给出变形腔顶部的z位置。
结束语
在今天的示例中,我们对可变形容器(本例中是气球)中流体的不同深度进行了模拟。全局方程用于求解体积保持不变的流体压力,同时也考虑了气球变形时流体深度的变化。
通过使用这种方法,我们不需要显示地求解 Navier-Stokes 方程,就可以解决流固耦合问题,从而节省了大量的计算资源。如果您对这种类型的模型感兴趣,或想了解更多关于这种模型的细节,请与我们联系。



评论 (0)