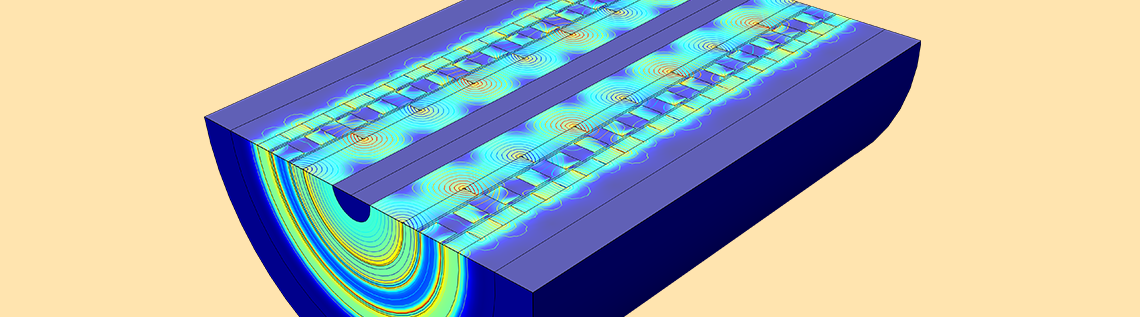
磁齿轮是利用永磁体或电磁体进行扭矩-速度转换的非接触式机构,用于多种可再生能源应用中,能提高风能、海洋能和飞轮储能的速度,以与电磁发电机的规格相匹配。和机械齿轮不同的是,磁齿轮内置过载保护,因工作时无摩擦而具有高可靠性,且无需润滑。今天,我们将讨论如何利用 COMSOL Multiphysics 模拟二维和三维的磁齿轮。
磁齿轮的构造和工作原理
磁齿轮一般包含三个转子,每个转子的磁极对数均不同,由很小的空气间隙隔开。铁磁性钢磁极(中间转子)调整内外转子产生的磁场,并在空气间隙中生成空间谐波。经过调整的磁场经钢磁极与另一侧的磁场相互作用,从而传递扭矩。
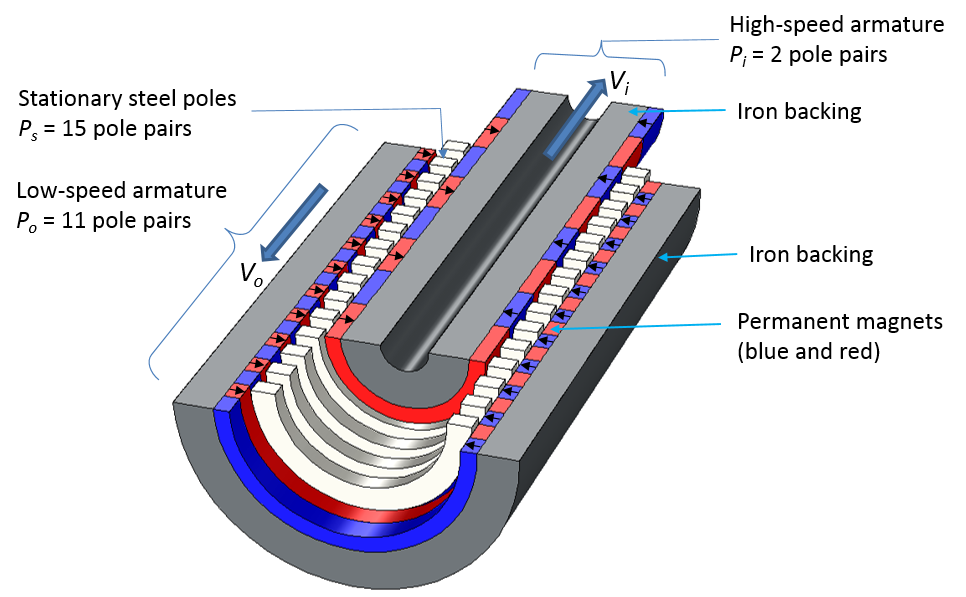
下图说明了典型磁齿轮的工作原理。为简单起见,我们选择直线磁齿轮结构。不过,它的工作原理还是与旋转磁齿轮相同。在这个结构中,模型的外部转子包含 11 对磁极,内部转子包含 4 对,中间转子包含 15 对。它们分别记作P_o、P_i和P_s。
内部转子上的 4 对磁极产生一个 4 次谐波占主导的磁场。然后该磁场经 15 对钢磁极的调整,产生一个 11 次谐波占主导的磁场。调整后的磁场与外部转子产生的可传递扭矩的 11 次谐波占主导的磁场相互作用。扭矩由此产生,因为此时外部转子产生的磁场谐波分量与调整后的内部转子磁场产生的谐波分量相匹配。
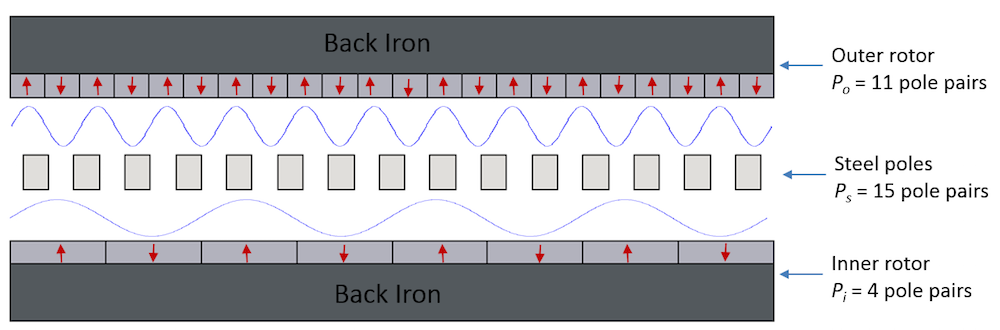
上方的示意图显示了直线磁齿轮的谐波分量。红色箭头表示永磁体的磁化方向。蓝色曲线显示内外部转子产生的磁场。图中未显示转子间的空气间隙(虽已放大)。
为使扭矩密度最高,每个转子的磁极对数应遵循以下关系:
为使传递的扭矩最大,所有三个转子的磁极对和角速度之间的关系应如下:
其中\omega_i、\omega_o和\omega_s分别表示内部转子、外部转子和钢磁极的速度。如果中间转子保持静止,速度和磁极对的关系则为:
P_i、P_s和P_o的最佳组合是使扭矩的波动最小。这样的波动主要由齿槽扭矩引起,这是由永磁电机和钢磁极之间的磁场相互作用而产生。使齿槽扭矩最小的参数称为齿槽因子。它表示为以下方程:
其中,LCM 指最小公倍数。当C_f = 1时,齿槽扭矩最小。此处展示的所有示例均满足该条件,且铁磁性钢磁极保持静止。
磁齿轮的类型
根据工作方式,磁齿轮可分为三种类型:直线磁齿轮 (LMGs)、同轴磁齿轮 (CMGs) 和轴向磁齿轮 (AMGs)。对于直线磁齿轮和同轴磁齿轮,磁通量通常沿轴心线径向向内或向外生成。然而对于轴向磁齿轮,磁通量线创建后则平行于转子轴。在本篇博客文章中,我们将利用 COMSOL Multiphysics 展示这三种磁齿轮的示例。
同轴磁齿轮
同轴磁齿轮包含三个磁极对数不同的同心转子,如下图所示。内部转子由八个永磁体 (PMs) 和一个软铁轭组成,软铁轭形成向外的磁通量,使 2 对磁极聚焦于转子。外部转子包含 20 个永磁体和一个软铁轭,软铁轭形成向内的磁通量,使 5 对磁极聚焦于转子。在内外转子中,永磁体按照海尔贝克阵列结构排列。七块钢置于中间的静止环中,钢块之间的间距相同,形成一个包含 7 对磁极的静止转子。
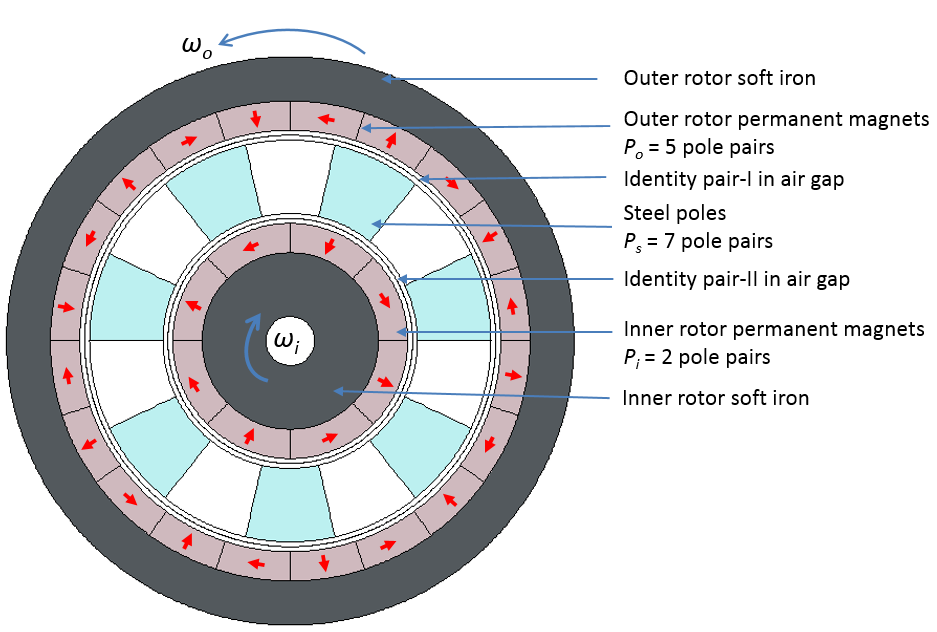
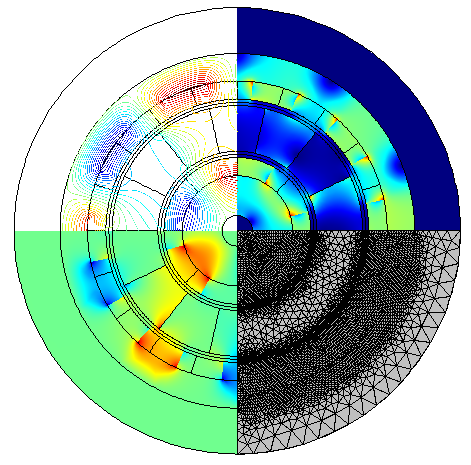
左图:同轴磁齿轮示意图,显示内部转子、外部转子和静止钢磁极。红色箭头表示永磁体的磁化方向。永磁体这样排列可以使内部转子成为向外磁通量的焦点,外部转子成为向内磁通量的焦点。右图:第一到第四象限依次是:磁通密度(模)、磁矢势 (Az)、径向磁通密度 (Br) 和网格图。
本示例中选取的磁极对数使齿轮比为 5:2,作为齿槽因子的最小齿槽扭矩为 1。在 COMSOL Multiphysics 中,我们使用 “AC/DC 模块”中的旋转机械,磁场接口模拟同轴磁齿轮的二维横截面。因为该模型由三个独立零件构成,我们必须使用形成装配将这几个零件组装成一个装配并确定最终的几何,这样才能在空气间隙区域创建两个独立的一致对。
我们使用 “B-H/H-B” 曲线将非线性材料模型加入到软铁域中。不过,静止钢磁极片的模拟则是使用相对磁导率\mu_r=4000的线性材料。使用指定旋转速度功能可以使内外转子旋转。通过计算力功能,使用 Maxwell 应力张量法计算内外转子上的轴向扭矩。
上面的动画展示了磁通密度的表面图和磁矢势A_z的等值线图。其中外部转子顺时针旋转,内部转子逆时针旋转,并显示磁场的相互作用。
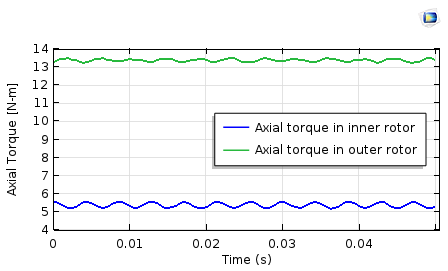
内外转子上的轴向扭矩曲线。内部转子上的扭矩波动较大(磁极对较少)。
您可以从“案例下载”中下载示例模型文件。其中可以找到几何序列文件、COMSOL 模型文件以及提供详细步骤说明的 PDF 文件。
轴向磁齿轮
轴向磁齿轮的工作原理与上面介绍的同轴磁齿轮相同。在本设计中,转子沿轴向一个个堆叠在一起,而非按径向排列,转子之间存在很小的空气间隙。因为磁场相互作用的表面很大,且三个转子的长度相同,所以与同轴磁齿轮相比,轴向磁齿轮的扭矩密度更大。左下图描绘了典型的轴向磁齿轮三维构造。
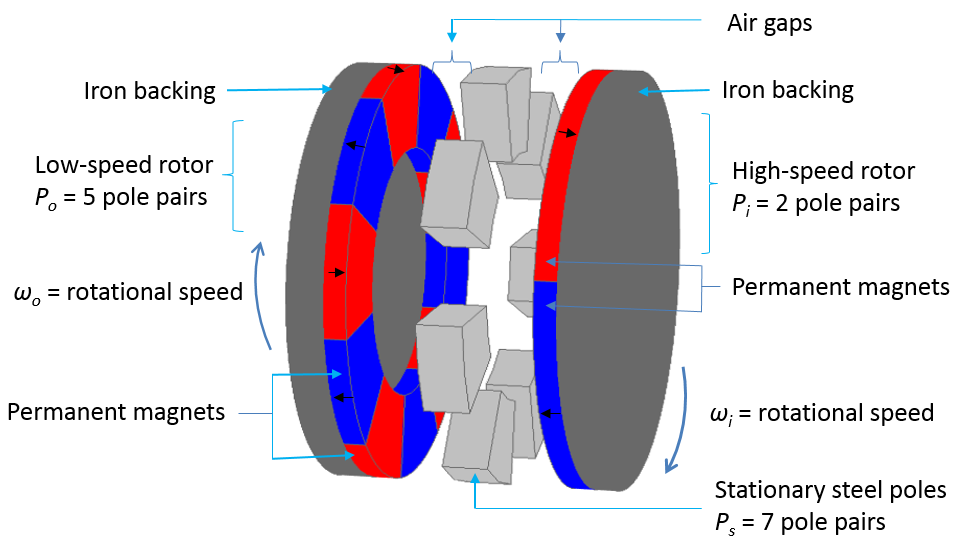
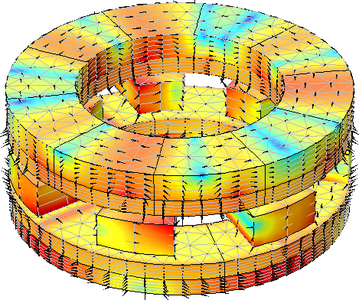
左图:轴向磁齿轮示意图,描绘了低速转子、高速转子和静止钢磁极。黑色箭头表示永磁体的磁化方向。右图:该仿真显示了磁通密度(使用对数刻度的表面图以及面上箭头图)和网格图。
请下载教程,尽情探索模型设置背后的所有细节。这个特别的示例包含了一些模型文件,用于使用参数化扫描进行稳态研究,还包含了一个轴向磁齿轮的全三维时域仿真,其中使用了旋转机械,磁场接口。其中还包含了一些稳态研究和时域研究的仿真结果。
上面的动画显示了磁通密度模的表面图和面上箭头图。其中高速转子顺时针旋转,低速转子逆时针旋转,并显示磁场的相互作用。
实际上,通过解算高速转子和低速转子之间不同角位置的稳态研究,可以获取磁齿轮的扭矩传递。通过稳态研究中的参数化扫描可以改变角位置。但是,对于瞬态仿真,则需要建立瞬态研究。有趣的是,您将会从这两项研究中得到完全相同的扭矩传递。
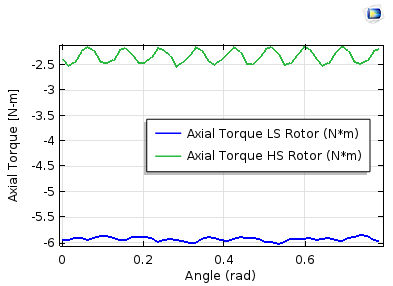
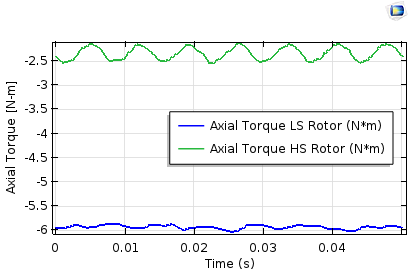
内外转子上的轴向扭矩曲线。左图:稳态研究和参数化扫描。右图:瞬态研究。高速转子上的扭矩波动较大(磁极对较少)。
直线磁齿轮
直线磁齿轮的运用相当广泛。例如,在油气行业,它们为钻井电机提供传动,将高速度转换成钻井所需的高扭矩。这类磁齿轮也可与直线同步机械结合使用,作为电动汽车的自由活塞发电机,同时产生交流发电用于交流能相关的各种应用。
典型的直线磁齿轮构造如下图所示。该齿轮由三个转子构成,其中两个为直线移动的电枢(也称作转子),其间为静止钢磁极。因为该几何在方位角方向上对称,所以我们可以利用二维轴对称几何求解。在此处展示的示例中,我们假设所有转子的长度相同,且在运动方向上无限长。该条件意味着我们只需模拟几何的一个扇区。
我们使用 COMSOL Multiphysics 中的磁场接口和移动网格接口建立模型。因为直线周期没有内置的周期性边界条件,我们就利用广义拉伸算子为低速电枢和高速电枢都创建一个定制的周期性边界条件。如要参考相关的示例,请阅读上一篇博客文章。
为计算高速电枢和低速电枢之间的电磁力耦合,我们使用时域仿真。您可以从“案例下载”中下载模型文件及其关联文档。
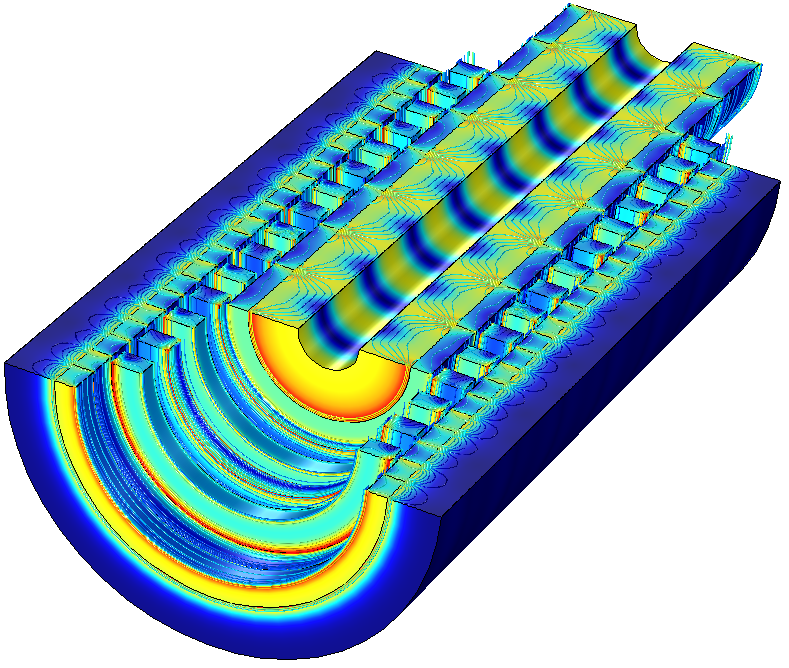
左图:直线磁齿轮的构造,展示了低速电枢、高速电枢和静止钢磁极。黑色箭头表示永磁体的磁化方向。右图:磁通密度模(表面图)和磁通密度的等值线图。还显示了径向分量。
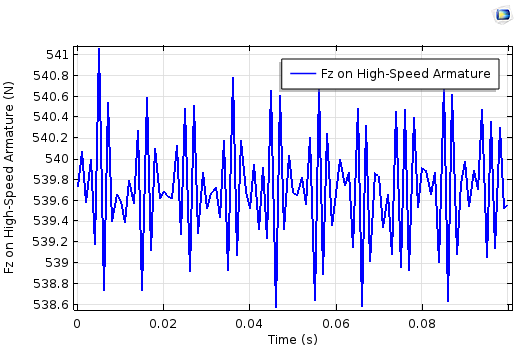
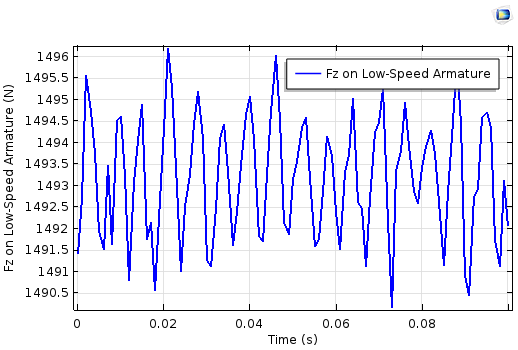
高速电枢(左图)和低速电枢(右图)上电磁力的z分量。
上面的动画描绘了磁通密度模的表面图以及磁通密度径向分量的等值线图。另外还显示了高速电枢和低速电枢的直线运动,以及磁场的相互作用。
总结
在今天的博客文章中,我们展示了可利用 COMSOL Multiphysics 模拟的主要磁齿轮类型,以及 “AC/DC 模块”中可使用的接口。进一步,通过稳态研究和瞬态研究演示了转子间扭矩传递的对比。
对于同轴结构和轴向结构,您可以利用旋转机械,磁场接口直接设置模型。但对于直线磁齿轮,则需要耦合磁场接口和移动网格接口,并定制周期性条件。



评论 (1)
Alex Wei
2019-05-12您好,非常感谢您的仿真案例,这对我有着重要的参考意义。但是冒昧地问一句,您这里有完整的仿真模型吗?因为很多仿真细节比如物理场和探针的设置在PDF里面并没有明确给出。我现在非常需要您完整的仿真模型,谢谢!