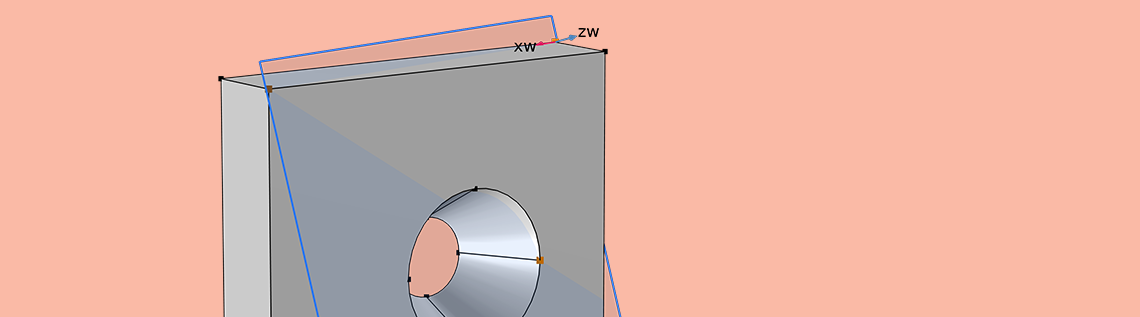
在建立固体力学模型时,我们经常会遇到这样的情况:有预设的载荷条件,却没有可以合理应用的约束条件。这时,根据几何形状的不同,我们可以采用一些不同的方法。这篇博文将为您介绍如何使用这些不同的方法,以及它们之间的细小差别。
一个固体力学问题
我们以一个经典的固体力学问题:一个简单的带孔平板模型为例来说明。让我们假设在顶部和底部有相等和相反的力。想象一下,也许这个部分通过一些固定装置连接到一些电缆上,并被置于张力之下。
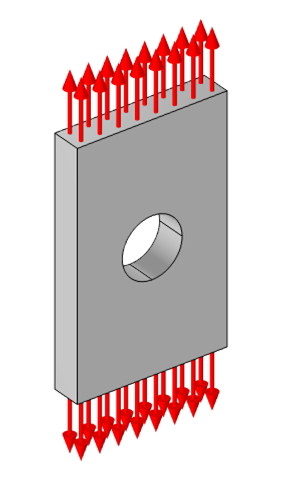
承受了拉伸载荷的中心有孔的平板的自由体图。
尽管我们可以建立一个固定装置和电缆的模型,以及与电缆连接的任何模型,但这可能比我们想象中要花费更多的精力。实际上我们只是想重点分析一个更大的系统中的一部分,所以把其他部分近似为一个垂直于板两端的边界载荷是可行的。
我们知道,一个零件受到大小相等、方向相反的力不会产生任何加速度,因此尽管零件会变形,但它不会运动。也就是说,即使我们不知道零件的位置或者方向如何,也可以自信地说此问题存在一个固定解。换句话说,就是施加的力可以在任意方向对齐,并且应力和应变的解仍然是相同的。
现在,当我们通过有限元方法求解一个固体力学问题时,我们并不直接求解应力或应变。相反,我们求解的是未变形状态下的位移(或变形)。应力和应变是根据位移场计算出来的。就本文而言,我们只讨论线性情况就足够了,但如果你对一些更高级的主题感兴趣,可以阅读下面的博文:
为了得到变形的解,我们确实需要在位移场上引入一组约束,这些约束必须足以约束所有自由体的位移和旋转,但不能影响应力和应变。本文将介绍实现这一目标的各种方法,具体取决于我们正在处理的几何形状。
使用对称平面
对于对称几何形状,有经验的结构分析者会立即发现有三个对称平面可以利用。我们可以画出与全局笛卡尔坐标系对齐的零件,并沿平行于xy-、yz-和xz平面的工作平面进行分割,这就把模型简化为原始模型的 1/8 子模型。将对称性条件应用在沿这些平面的三个面,将产生完全约束零件的效果。此外,这还具有减少模型计算量的好处。
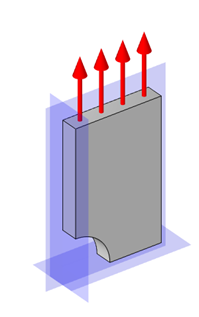
利用沿三个正交平面的对称性完全约束模型。
我们先看看这三个对称边界是如何约束零件的。对称边界要求在所选(平面)边界的法线方向上没有位移。因此,施加在平行于xy平面的面的对称条件是,该面在z方向上的位移为零,并且不能绕x轴和y轴旋转。
接下来,yz平行面上的对称条件还具有附加条件,即在x方向上不能有位移,也不能绕z轴旋转。绕y轴的旋转再次受到限制,但这不是问题。
最后,在xz平行面上的对称条件施加了一个额外约束,即在y方向上无位移。
因此,我们在位移和旋转上施加了一组三个正交约束,该零件受到了充分的约束,模型可以求解。为了使结果可视化,我们使用了一组三个三维镜像数据集,它可以帮助围绕一个平面镜像任何数据集,这样就可以使整个零件可视化。
不对称的零件
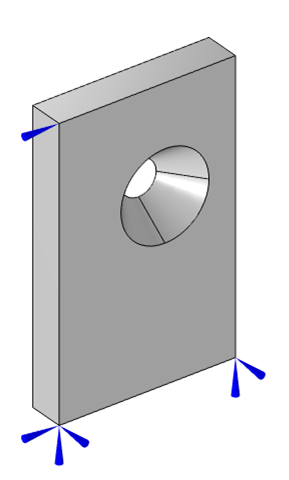
然而,通常我们很难遇到具有三个对称平面的零件。这时,我们可以在孔中引入一个锥形并更改它的位置来修改我们的零件,如下图所示。
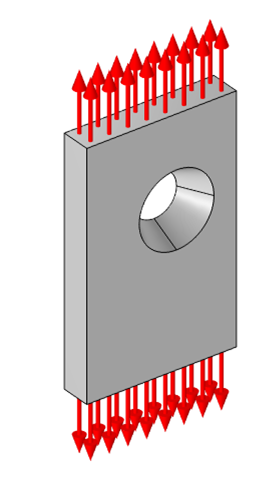
处于拉力下的带有偏心锥形孔的平板的自由体图。
在这种情况下,无法利用任何对称性,那么我们能做什么呢?实际上,我们可以采取四种不同的方法来解决这个问题。
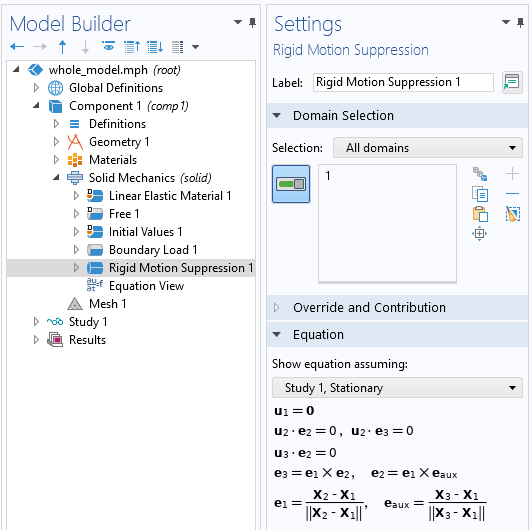
将刚体运动抑制特征应用于所有域以约束位移和旋转。
最简单的第一种方法是使用刚体运动抑制域约束功能。只需要将这个功能应用在模型的任何一个或者所有子域,它就将在后台应用一组约束,消除所有刚体位移和旋转。我们只要应用这个特征,模型就会求解。
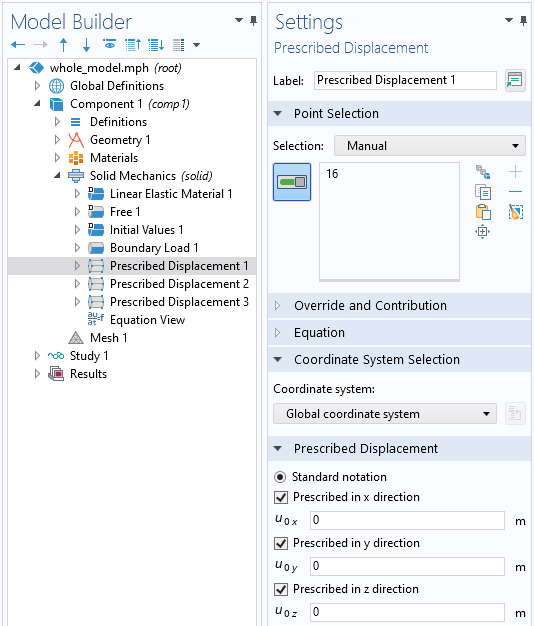
点-指定位移条件约束所有的自由体位移。
第二种方法是通过一组三个不同的点手动约束位移和旋转。为此,首先在几何体上选择一个点,然后在该点上施加一个指定位移条件,将x、y和z位移设置为零。
尽管我们可以选择任意一个点,但我们很快就会发现,最好在这个矩形零件的一个角上选择一个点。这个单一的约束足以消除所有刚体位移,并且不会对应力和应变场产生影响。
三点位移约束的可视化,约束所有自由体旋转和位移,但对应变场没有影响。
接下来,我们需要移除围绕三个正交轴的旋转。这可能有点棘手,尽管对于上面图中这种情况,比较容易操作,因为上图的几何图形与全局笛卡尔坐标轴对齐。所以,我们可以从完全约束的点开始,沿着直角坐标系方向寻找。
我们先从这个点沿着x轴看,直到找到另一个点。在这个点应用另一个指定位移条件来移除刚体旋转,但我们需要确保不施加一个会影响应变和应力的约束。另一种方法是,我们不想对这两个点之间的距离施加约束。因此,在第二点处,我们将约束y和z方向的位移,但不约束x方向的位移。这个约束分别消除了绕z轴和y轴的旋转。现在这个零件只能围绕x轴自由旋转,我们可以通过另一个点约束来消除这种自由旋转。
如果回到第一个完全约束的点,我们现在可以沿着y轴或z轴寻找,直到找到一个点。沿着z轴方向搜索,只要我们找到一个点,就可以施加一个指定位移条件,使y轴方向的位移为零。这将会防止零件围绕x轴旋转。同样,需要确保我们没有限制任何点之间的距离。如果不小心这么做了,就会出现局部高应力。
第二种方法实际上是第一种方法自动执行的手动操作。不过,这可能会引起一个问题:当没有三个点与笛卡尔坐标轴对齐时会发生什么?如果使用第一种方法刚体运动抑制,该特征将能够自动选择形成一个平面的任意三个点,并施加一组一致的约束。接下来,我们看看如何使用任意三个点进行约束,只要它们能形成一个平面。
第三种方法,我们使用相同的几何图形,但使用三个不与笛卡尔坐标轴对齐的点进行约束。首先我们需要定义一个工作平面,然后使用该工作平面定义一个坐标系,最后在指定位移条件下使用该坐标系。
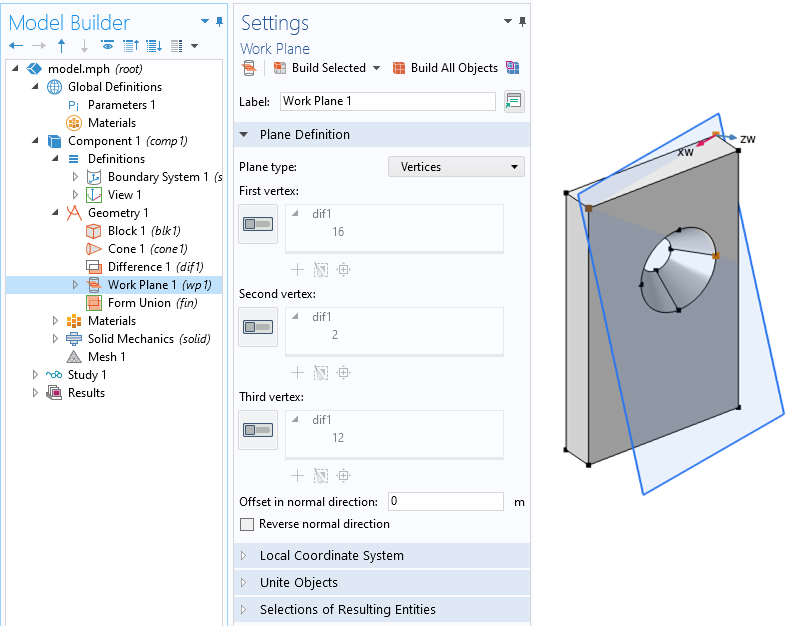
可以使用三个任意点来定义新的工作平面。
首先在几何中定义一个新的工作平面,平面类型为顶点,并选择三个不共线的点来定义平面。注意,我们选择的前两个顶点将定义这个平面的第一个局部轴。接下来,定义一个几何中的坐标系。将这个坐标系的框架设置为空间,并在 几何中的坐标系 设置中选择新的 工作 平面。
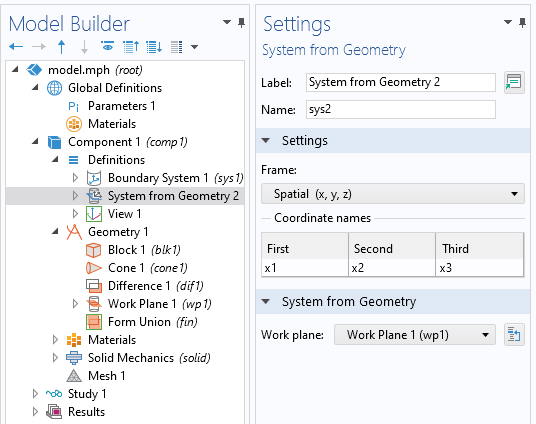
定义基于工作平面的坐标系。
然后,像之前一样,添加三个指定位移点条件,并为每个点将坐标系设置为几何中的坐标系。这三个点应该对应于在工作平面特征中选择的三个点。在第一个点上,约束所有三个位移。在第二个点(定义第一个局部轴的那一点),约束第二和第三方向的位移。在第三点,约束第三轴(平面法线)方向的位移。这种方法的优点是它不要求零件与笛卡尔坐标轴对齐。同样,刚体运动抑制特征也有相应的功能。
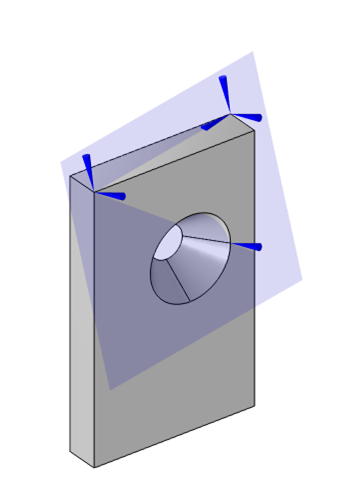
在由这三点定义的坐标系中,约束所有自由体旋转和位移的三点位移约束的视图。
第四种方法是解决没有三个点定义平面的几何体的特殊情况。当我们处理导入的网格文件时,可能会出现这种情况,比如在这个脊椎模型,它在原始网格上没有定义任何点。尽管我们可以在导入的网格上手动创建顶点,也可以对几何体的边缘进行分割以引入额外的点,但值得了解的是最后一种选择。
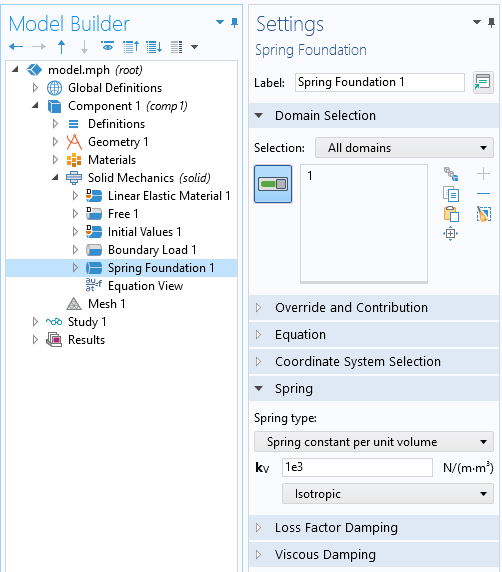
使用弹簧基座特征也可以约束位移和旋转,但如果弹簧常数足够小,就不会影响解决方案。
在第四种方法中,我们使用弹簧基座域特征,并将其应用于模型的所有域。这个特征在结构模型的每个自由度上,相对于其未变形的位置引入了一个人为的额外刚度。弹簧常数的大小是在模型中可以调整的因子。如果该值太小,就不能提供足够的数值刚度,模型就不能求解,但也不应该太大,因为这也会影响结果。在实践中,开始我们先选取一个非常低的值,然后慢慢增大,直到模型求解。虽然只有在极少数情况下,这种技术是严格必要的,但它仍然值得了解。
部分对称的零件
还有一种非常常见的情况,我们还需要考虑,那就是具有某种对称性的零件。对于这种零件,不能使用刚体运动抑制特征。
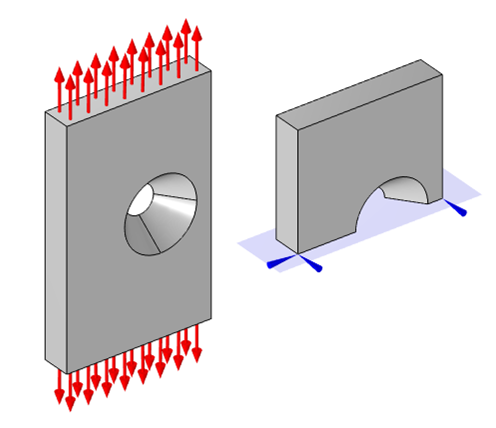
利用半对称性需要两个点位移约束,以消除平面中的平移和绕垂直于平面的轴的旋转。
对于模型中的单一对称平面(或两个平行的对称平面),我们必须在平面上选择两个点,并使用指定位移点条件来约束它们,使得在该平面上没有位移并且没有围绕该平面法线的旋转。如果有两个相互成一定角度的对称平面,则在其中一个平面上选择一个点,并对其进行约束,使其不能沿两个平面相交线所描述的方向移动。
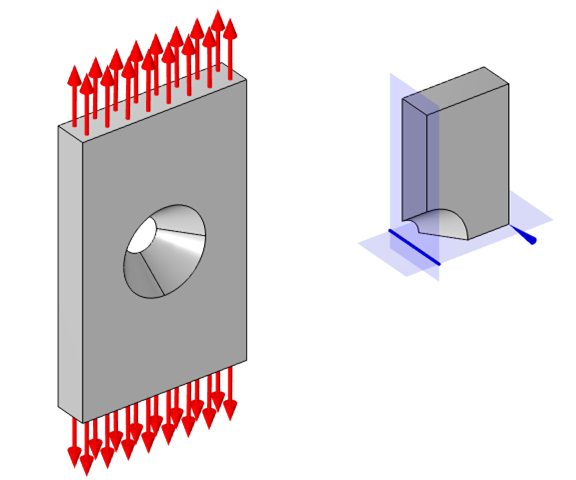
对于有两个对称平面的几何形状,通过单个点约束移除沿平面相交线的平移。
对于这类模型结果的展示,了解如何将位移视图放置在中心也很重要。假设我们希望模型需要结果可视化,位移以孔为中心,我们可以做的是引入一个平均耦合算子,并在孔的边界上定义它。然后,在可视化位移结果时,可以在变形子节点中减去这个平均位移,如下面的屏幕截图所示。
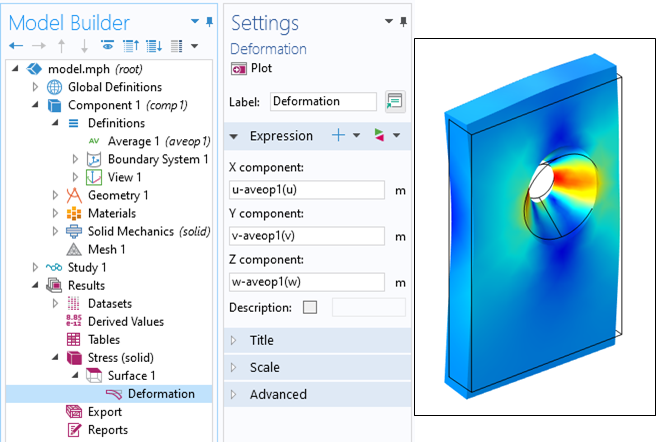
使用平均算子将围绕孔中心的位移的可视化重新居中。
对无约束零件建模的总结性思考
综上,我们介绍了模拟 3D 零件的技术,这些零件只有一组平衡载荷,但没有约束。最简单的方法是使用刚体运动抑制特征,但由于其他对称条件,我们有时需要通过一组点进行约束。
对于 2D 结构模型,我们应用了类似的、但更简单的方法。对于不对称的零件,必须将一个点xy平面中完全约束,并且必须约束另一点以防止绕平面外的z轴旋转。对于具有一个对称平面或平行对称平面的 2D 模型,只需要一个点位移约束来防止沿对称平面的运动。对于具有相交对称平面的 2D 模型,不需要额外的约束。对于 2D 轴对称模型,只有沿z方向(平行于对称轴)的位移必须在任何单个点处受到约束。
这些方法在处理涉及热膨胀的问题时特别有用,并且可用于任何研究类型,包括稳态、时域、频域或特征频率。对于结构分析人员,这些方法是非常强大的工具。



评论 (10)
在喜 向
2022-04-29博客上很多文章都很有参考价值,但是没有提供分享到社交媒体(微信,微博,QQ空间等)的功能,不方便收藏和后来查阅。
hao huang
2022-04-29 COMSOL 员工感谢您的建议,您可以先尝试使用收藏网页,同时我们已向技术部门反馈相关问题。
在喜 向
2022-05-08收藏起来慢慢看。
永欣 樊
2023-02-25图《三点位移约束的可视化,约束所有自由体旋转和位移,但对应变场没有影响》中,最后一点(左上角)的约束方向错了,应该是朝向y轴
Liwen Yang
2023-03-08 COMSOL 员工感谢您的反馈,我们将向相关部门反馈该问题。
Jiahui Yin
2024-02-19这种选取点进行约束的方式是否会对拓扑优化结果产生影响呢?
屹磊 金
2024-02-20 COMSOL 员工三点约束是限制刚体位移和刚体转动的,适用于外力的合力、合力矩为0的情况。三点约束在设置合理的情况下不会影响结构的应力状态和变形,但是最终呈现出来的位移会受三点选取的影响,如果您的优化目标是位移相关的那点的选取可能会对结果产生影响。
少敏 谷
2024-03-27一个放在桌面上的物体,法向方向施加外部载荷,同时内部包含热膨胀力。这种体系可以在辊支撑面(与桌面接触面)施加点约束吗?
东臣 李
2024-08-29你好,我看这篇文章中,添加刚体运动抑制未说明求解位移位移可能不正确,相对位移正确,应力正确,而绝对位移不正确,而在这篇博客(//www.denkrieger.com/blogs/how-to-provide-structural-stability-in-thermal-expansion-simulations)中作了上述说明并有了解释:这时应力是相同的,但变形后的形状看起来不同。事实上,他们的不同之处在于刚体运动。当我们手动提供刚体运动抑制时,我们从无数个解中选出一个。自动刚体运动抑制可能选择了另一个。因此,刚体运动的位移可能不同,但应变和应力是相同的。因此,我想请问,这两篇文章哪个正确?还是说老版本刚体运动抑制存在问题,而新版本改进了这项功能而不存在问题了?
Kaixi Tang
2024-08-30 COMSOL 员工您好,对于刚体运动抑制,如这篇博客中所提到的一样,它是软件自动执行的“三点约束”方法。由于这三个点的选取是任意的,那么就可能会导致您描述的手动使用刚体运动抑制(三点约束)和自动刚体运动抑制的位移结果出现区别。所以当您使用刚体运动抑制后,查看位移结果可能是不可信的,但是应力和应变(相对变形)信息是可信的。