
今天,来自 Veryst 工程公司的 Nagi Elabbasi 将作为客座博主和认证咨询机构顾问与我们一起分享有关优化声子晶体带隙设计的仿真研究。
声子晶体是一种相当独特的材料,它可设计出特殊的带隙。随着对此类材料需求的不断提高,人们对声子晶体仿真研究产生了浓厚的兴趣,针对带隙的优化是其中最热门的课题。本文将为您展示如何使用 COMSOL Multiphysics 这一可靠工具进行此类研究。
声子晶体是什么?
声子晶体是一种人工制造的结构或材料,可对其周期性结构或几何属性进行设计,以此影响机械波的传播特性。设计制造声子晶体时,人们能够在特定的频率范围内隔离振动。特定频率范围内,也称为带隙,带隙内的振动会因受到周期性结构内波干涉的影响而衰减。这一行为与一种更广为人知的纳米结构相似,这一纳米结构便是半导体应用中光子晶体。
优化声子晶体带隙是一项具有挑战性的任务。我们 Veryst 工程公司的研究人员发现 COMSOL Multiphysics 正是处理这类难题的宝贵工具。
建立声子带隙分析
要在周期性结构中创建带隙,一种方法是使用由坚硬的内核材料与柔软的外部基体材料构成的晶胞。其构型如下图所示。
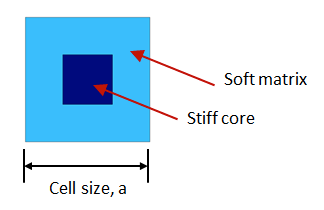
晶胞示意图。晶胞由坚硬的内核材料与柔软的外部基体材料构成。
对声子晶体的频率响应进行计算,仅仅需要对周期性晶胞进行分析,及利用覆盖一定波矢范围的布洛赫周期性边界条件。相对较小范围的波矢即可覆盖所谓的不可约布里渊区(irreducible Brillouin zone,简称 IBZ)的边缘。在二维矩形结构中,IBZ(下图所示)从 Γ 沿着 X、M 后回到 Γ。
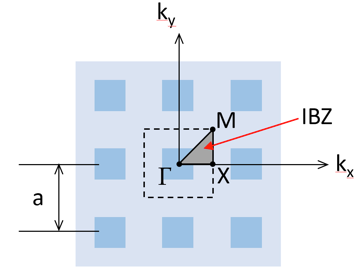
二维正方形周期性结构中的不可约布里渊区。
布洛赫边界条件(一维时又称 Floquet 周期性边界条件)可约束周期性结构的边界位移,表达式如下:
其中kF表示波矢。
源端和目标端分别在晶胞的左右边缘和上下边缘各应用一次。此类型的边界条件可在 COMSOL Multiphysics 中获得。由于边界条件的性质,我们需要一个复杂的特征值求解。系统方程组属于厄密特矩阵,得出的特征值为实数,也就是假定模型是无阻尼的。COMSOL 软件能够自动运行计算,这一步骤因此变得轻松简单。
我们对特征值求解分析作参数化扫描,其中一个参数k的范围为 0 到 3。这里,0 到 1 定义为覆盖不可约布里渊区 Γ-X 边缘的波数,1 到 2 定义 为覆盖 X-M 边缘的波数,2 到 3 则定义为 M-Γ 边缘的波数。对于每一个参数,我们将求解最低价本征频率,然后绘制每一个k值时波的传播频率。绘图中的带隙代表其中不存在波传播的区域。暂且不论复杂的晶胞模型,完成分析只需几分钟时间。由此可以总结,如果你以特定的带隙位置为目标,或者想要使带隙宽度最大化,那么使用晶胞是一种高效的优化手段。
执行优化研究
为了清晰阐释这类应用,我们对上图的周期性结构进行了模拟,晶胞尺寸为 1 cm × 1 cm,内核材料为 4 mm × 4 mm;基体材料的模量为 2GPa,密度为 1000kg/m3;内核材料的模量则为 200 GPa,密度为 8000 kg/m3。下图显示 60 kHz和 72 kHz 之间禁止波传播的频率范围。
kg/m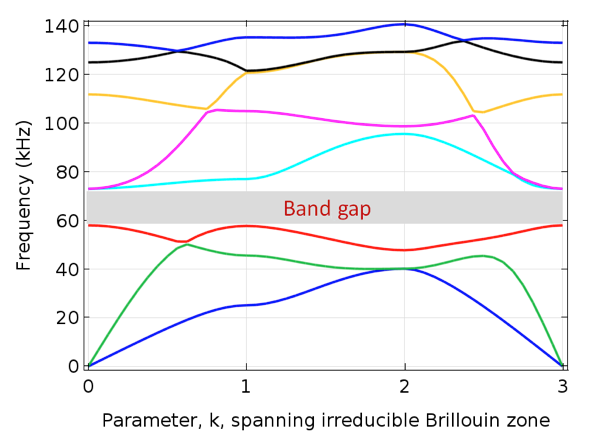
选定晶胞参数的频带示意图。
为了演示如何利用带隙概念实现隔振,我们将模拟上述周期性结构中的晶胞组成的“11 × 11”的晶格结构。这些晶胞承受的激励频率为 67.5kHz(带隙中)。
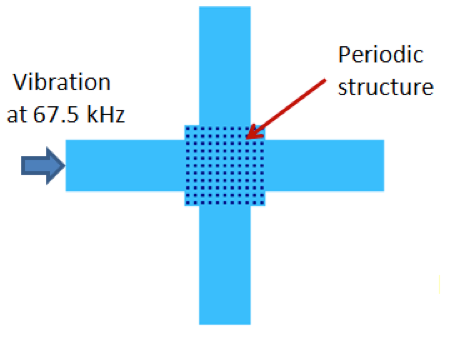
该结构用于演示带隙中针对施加频率的隔振。
下方动画重点演示了晶胞结构的振动响应。通过结果,我们可以了解到周期性结构能够十分有效地将施加的振动与剩余结构隔离开。即使减少周期性晶胞的使用数量,仍然可以很有效地隔振。
频率为 67.5 kHz 时,振动响应的动画。
请注意,当频率在带隙之外时,周期性结构不会隔振。此时的响应情况请参考下图。

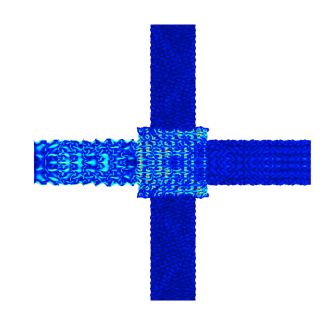
于带隙之外频率的振动响应。左图:27kHz。右图:88kHz。
想要学习更多关于二维带隙模型的知识,请前往 “COMSOL 模型交流”。
参考文献
- P. Deymier (Editor),Acoustic Metamaterials and Phononic Crystals, Springer, 2013.
- M. Hussein, M. Leamy, and M. Ruzzene,Dynamics of Phononic Materials and Structures: Historical Origins, Recent Progress, and Future Outlook, Appl. Mech. Rev 66(4), 2014.
特约作者介绍




评论 (13)
Cong Gao
2017-10-27Hi! Thank you for sharing.
I am trying to do a 3D model, but how should I define the k vector in three direction. And what if I just want the structure’s periodic in one direction (say along x-axis).
Many many thanks
宇航 秦
2017-11-06Cao Cong,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:www.denkrieger.com/support
Email:support@comsol.com
谢谢!
晗 李
2018-05-23Thank you for sharing!
For further information, would you like to teach me how to make the gif which shows vibration response of the SC. Thanks a lot!
Tengyue Gao
2018-10-19Hi 李晗 ,
Thank you for your comment.
For questions related to your modeling, please contact our support team.
Online support center:https://www.comsol.com/support
Email:support@comsol.com
磊 赵
2018-12-20请问这个模型的下载名称是什么,怎么找不到?
Nagi Elabbasi
2018-12-20I re-posted the model to the Application Gallery: Here is an updated link:https://www.comsol.com/community/exchange/642/
磊 赵
2018-12-21THANK U
Anonymous
2019-07-16Hi!
Thank you very much for your sharing!
I have some questions that have been bothering me for a long time.
Firstly, I have been working on Band Gap calculation recently, and I am confused how to make my calculation for Shear Horizontal Mode (SH wave) because I can’t find anywhere that I can set to tell COMSOL to make it for SH wave or SV wave or Lamb wave.
Secondly, I find that PML has no effect on absorbing wave when it is used to simulate transient wave motion by using solid mechanics module.
Can you give me some advice?Thanks a lot!
地 余
2019-08-15Thanks!
建 宋
2023-10-11Hi!thanks for sharing.I want to ask how to select the number of the k in different simulation. Thanks so much
Yuqing Ge
2023-10-13 COMSOL 员工Hi!
The wave number k varies from 0 to pi/Li (Li is the length of your periodic unit cell). Then define the direction of k that we’re going to sweep. The direction depends on irreducible Brillouin zone, where the direction between any two vertices should be swept.
Huaiqian Li
2024-06-03三维的Floquet边界条件怎么写
Hao Li
2024-06-05 COMSOL 员工您好!
感谢您的评论。
二维/三维声子晶体的Floquet条件设置需要根据晶格形式设置扫描路径,建议您先根据您的声子晶体的晶格形式写出其对应的不可约布里渊区,再依次扫描。晶格形式及不可约布里渊区的相关概念建议查阅相关的书籍或论文学习。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:www.denkrieger.com/support
Email:support@comsol.com
谢谢!