在 COMSOL^®中对表面等离激元进行建模

人们对被限制在沿表面传播的电磁波，例如表面等离激元(SPPs)，有很大的研究兴趣，因为它在纳米级光控制中有着潜在应用。在这篇博客中，我们将讨论如何设置一个仿真来可视化表面等离激元的传播以及频率-传播常数色散关系。

表面等离激元简介

电磁学的控制方程，也就是麦克斯韦方程组，可能看起来很简单，但它们的含义却极为广泛和深刻。因此，传播的电磁波可以以各种众所周知的形式存在，如平面波、球面波、高斯波束，以及一些鲜为人知的形式，包括贝塞尔波束、艾里波束和涡旋波束。还有一些被限制在空间内传播的电磁波，例如在金属或介电波导中传播的波导模式。

此外，还有一种特殊类型的被限制在平面上的电磁波。这种类型的波沿切向表面传播，并在垂直方向上呈指数衰减。与相同频率的自由空间波长相比，它的波长通常更小。因此，这种类型的波为光子的纳米级控制和操作提供了一个潜在的技术平台，从光通信和信息处理到太阳能收集和数字显示，这在许多应用中都是需要的。这种类型的波是在金属-介电界面上发现的，现在被称为表面等离激元(SSP)。等离激元是指金属中电荷的集体振荡。自发现以来，人们已经了解到许多材料系统都支持这种类型的表面波，例如接近其声子共振频率的极性介电材料和接近其激子频率的半导体材料。相应的表面波分别称为表面声子偏振子和表面激子偏振子。

无论支持的介质和微观细节如何，不同类型的表面波背后的宏观物理学是相似的。在下面的章节中，我们将重点讨论介电和金属界面之间的等离激元建模。然而，需要注意的是，本文所涉及的建模技术也可以通过一些适当的修改，以类似的方式应用在其他表面波，如 Sommerfeld-Zenneck 波和 Dyakonov 波。

最简单的表面等离激元色散的推导

为了清楚地了解什么是表面等离激元，让我们研究一下支持表面等离激元的最简单的系统，即体金属-介电界面。想象一个在平面上y=0的金属-介电界面xz。介质区为y>0，金属区为y<0。由于xz平面内没有首选方向，因此在不丧失一般性的情况下，重点研究在x方向传播的表面波。传播平面被定义为传播方向和表面法线所跨越的平面。在这种情况下，传播的平面就是简单的xy平面。一般来说，传播的电磁波可以分为 s 偏振和 p 偏振，具体取决于电场或磁场是否垂直于传播平面。我们首先考虑 p 偏振（或 TM 波）的情况。

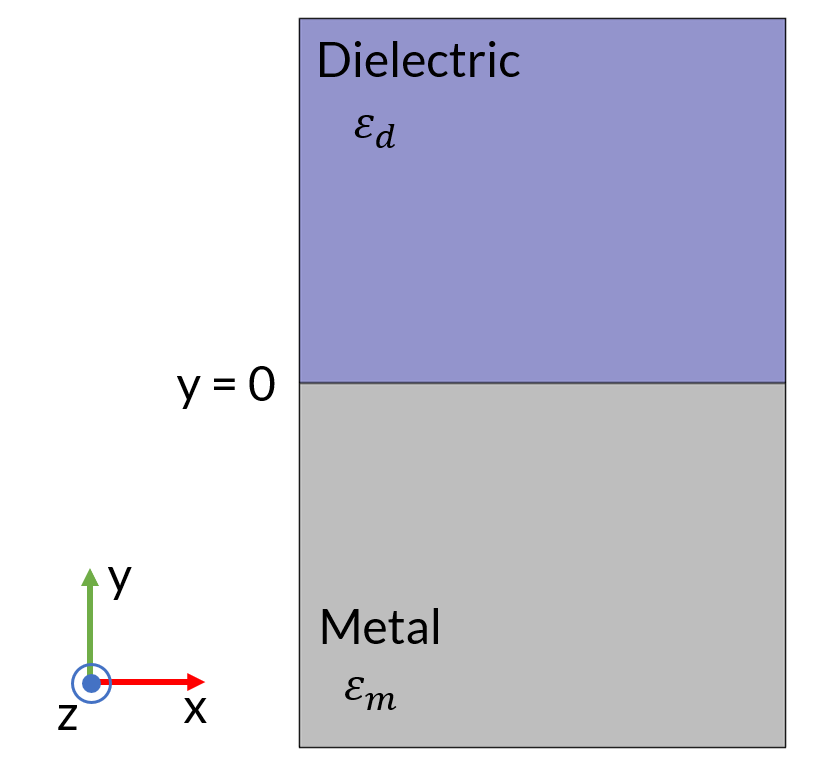
位于y=0方向的金属–介电界面。该系统支持沿x方向传播并在y方向上呈指数衰减的表面等离激元。

由于我们对沿x方向传播并沿y方向衰减的 TM 模表面波感兴趣，因此可以将电介质和金属中的电场和磁场写为

(1)

(2)

(3)

(4)

其中+和–上标分别表示y>0和y<0的数量。k_{SPP}是复杂的表面等离激元传播常数。k_y^+和k_y^-都是正实数，描述了远离金属介电界面的场衰减。根据边界条件，我们知道电场和磁场的切向分量以及电位移场的垂直分量在金属-介电边界y=0上是连续的。因此，E_x^+=E_x^-=E_x,H_z^+=H_z^-=H_z,\varepsilon_dE_y^+=\varepsilon_mE_y^-=D_y。根据麦克斯韦方程组，我们知道\nabla \cdot \vec{D} = \rho_{ext}。由于没有外部电荷，并且介电常数在y>0和y<0分别是恒定的，因此必须在两种物质中保持\nabla \cdot \vec{E} = 0,将其与等式 2 与等式 4 相结合，得到

(5)

(6)

可以简化为

(7)

从此关系中，我们可以看到为什么表面等离激元只存在于电介质Re(\varepsilon)>0和金属Re(\varepsilon)<0之间。要使场在y方向上衰减，k_y^+和k_y^-都必须是正的，这意味着\varepsilon_d和\varepsilon_m必须具有相反的符号。为了推导k_{SPP}的表达式，我们使用亥姆霍兹波动方程\nabla^2 \vec{E}-\frac{\varepsilon \mu}{c^2} \frac{\partial^2E}{\partial t^2}=0，该方程是从两个麦克斯韦曲线方程导出的。将等式 2 和等式 4 代入亥姆霍兹方程，得到

(8)

(9)

其中，k_0=\omega/c是自由空间波数。最后，结合等式 7–9，我们得出表面等离激元传播常数的表达式

(10)

实部k_{SPP}通过\lambda_{SPP}=\frac{2\pi}{Re(k_{SPP})}与表面等离激元波长相关，而虚部描述了表面等离激元传播损耗。通常，\varepsilon_d和\varepsilon_m是频率相关的，因此k_{SPP}也是频率相关的。k_{SPP}和频率的关系通常是我们想要知道的用于在系统中表征表面等离激元。

请记住，上述讨论纯粹基于表面等离激元是 TM 波的假设。对于 TE 波的可能性，可以简单地遵循相同的推导步骤，并证明所有场振幅必须为零。这意味着 表面等离激元 仅以 TM 波的形式存在，这也是表面等离激元的一个显著特征。

模拟表面等离激元的传播和色散

在本节中，我们将讨论如何使用 COMSOL Multiphysics^®软件的仿真和建模功能来可视化上述推导的物理结果。由于表面等离激元是空间受限的传播波，我们可以从其他波导建模示例中得到启发，例如介质平板波导教程模型。为确保我们正确设置了模型，作为有效性检查，将在银（金属）和空气（电介质）的界面中模拟表面等离激元表面等离激元。银的介电函数由等离子体频率值约为 9.6 eV 的 Drude 模型很好地描述。对于此模型，我们可以方便地使用 COMSOL 软件内置材料库中的银材料属性。在模型的左侧和右侧边界上施加一个数值端口。打开激励的左侧端口将启动表面等离激元，而关闭激励的右侧端口将吸收表面等离激元而不反射。为了获取两个端口上的模态场，分别添加了两个边界模式分析研究步骤和一个频域研究步骤。

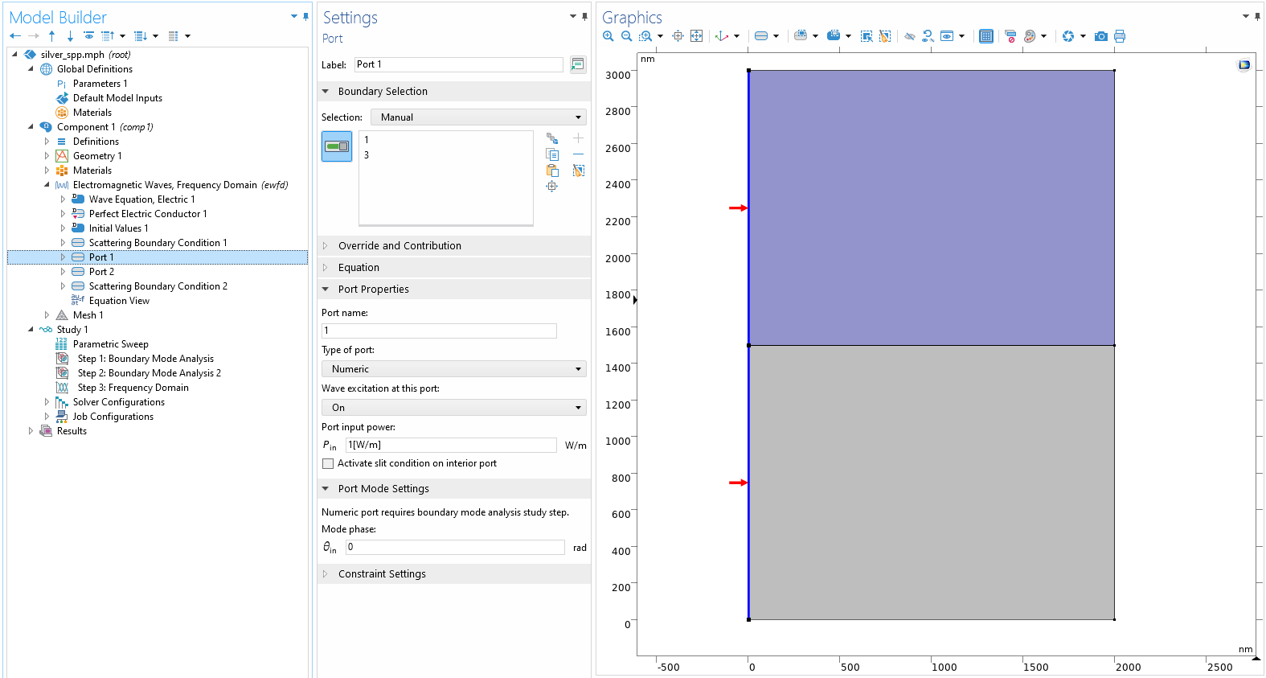
在左右边界分别施加了两个端口，用于表面等离激元的激励和终止。为了获取端口上的模态场，在频域研究步骤之前添加了两个边界模式分析研究步骤。

运行模拟后，我们可以很容易地看到表面等离激元的传播。从左到右，下面的动画分别显示了 3.54 eV、3.1 eV 和 2.07 eV 光子能量下的表面等离激元。正如预期的那样，场沿x方向传播并沿y方向衰减。由于吸收力强，金属侧的衰减更快。值得注意的是，表面等离激元波长（实部k_{SPP}）和传播损耗（虚部k_{SPP}）随光子能量或频率而显著变化。为了捕捉频率和k_{SPP}之间的定量关系，我们使用可变频率作为y轴和ewfd.beta_1作为x轴绘制它们（由下面动画中的圆形标记显示）。ewfd.beta_1是一个复数，但在绘制它时，默认只考虑它的实部。在研究表面等离激元时，习惯上将品质因数（通常称为 Q 因子）定义为实部和虚部k_{SPP}的比率。当k_{SPP}具有较小的虚部（相当于较大的 Q 因子）时，表面等离激元可以在衰减之前相对于其波长传播很长的距离。对于生物传感器和光开关等实际应用，通常需要较大的 Q 因子。Q 因子可以方便地绘制为色散曲线的颜色表达式。在这里，我们选择较亮的颜色来表示较高的 Q 因子，选择较深的颜色来表示较低的 Q 因子。此外，还添加了一条虚线\omega=ck_0，通常称为浅色线。浅色线是自由空间光子的频率-波数色散关系。最后，将方程 9 中的解析表达式绘制为实线。从动画中可以看出，模拟色散和解析表达式表现出很好的一致性。

模拟 3.54 eV、3.1 eV 和 2.07 eV 光子能量下的表面等离激元传播。箭头表示电场方向和强度。

下面的色散图非常能代表贵金属中的表面等离激元色散。该图有助于深入了解表面等离激元的特征。最重要的是，它表明表面等离激元的色散曲线始终位于光线的右侧。这意味着表面等离激元波长总是小于自由空间光的波长。这就是为什么表面等离激元可以用作压缩光波长以实现光场更集中的方法。此外，自由空间光波数和表面等离激元传播常数之间的不匹配意味着我们不能仅仅通过将光照射到金属表面来激发表面等离激元，还需要一些外部机制来进行波矢量匹配。表面等离激元的激发通常是通过使用棱镜的全内反射，光栅的衍射，散射体的散射或穿过电子束来完成的。使用这些技术的目的是准备电磁场，使其波矢量与相同频率的表面等离激元的波矢量相匹配。

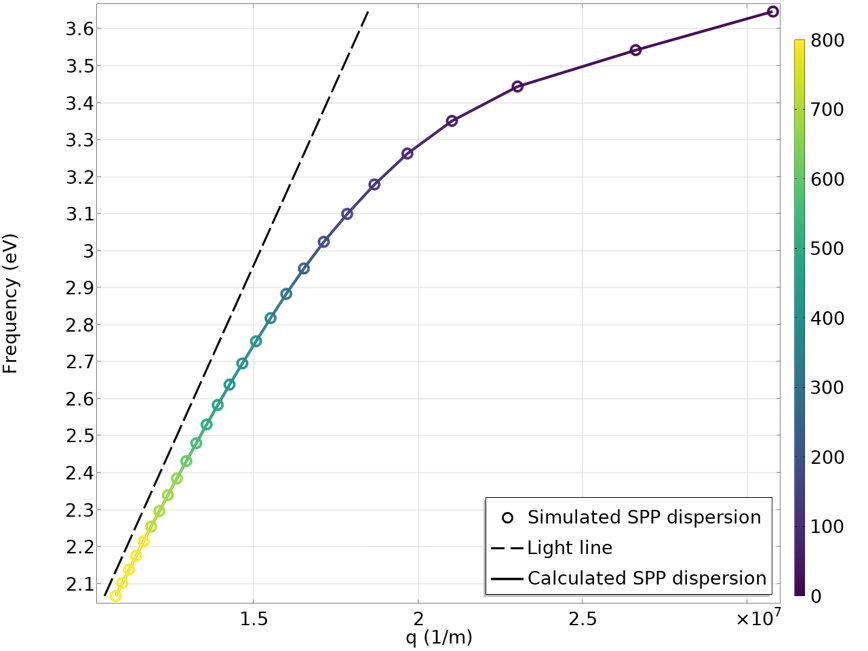
表面等离激元在银和空气界面处的模拟的频率-波传播常数色散图。正如预期的那样，模拟结果（圆）与分析计算（实线）一致。自由空间光色散或光线由虚线表示。颜色表示表面等离激元的Q因子。

金属薄膜中的表面等离激元

尽管模拟体金属-介电界面中的表面等离激元可以作为表面等离激元传播和色散的很好的示例，但这是一个相当简单并且在物理上无趣的示例。在本节，我们将介绍一个更有趣的案例，即由介电层覆盖的金属薄膜。在这种系统中，顶面和底面都支持表面等离激元。如果金属膜足够薄，那么顶面的表面等离激元和底面的表面等离激元之间的耦合将导致模式杂化。其结果是形成对称和反对称模式。这种情况下的物理场类似于耦合机械谐波振荡器的物理场。在这种特殊情况下，我们模拟了 12 nm 铝膜，周围环绕着折射率为 2 的 4 nm 介电层。使用边界模式分析研究步骤，我们在色散曲线中发现了两个表面等离激元分支。Q 因子较大的上分支是对称模式，而 Q 因子较小的下分支是反对称模式。

模拟表面等离激元在两个介电薄膜之间的铝薄膜上的传播。铝膜顶面和底面中表面等离激元的杂化形成对称（左）和反对称（右）模式。

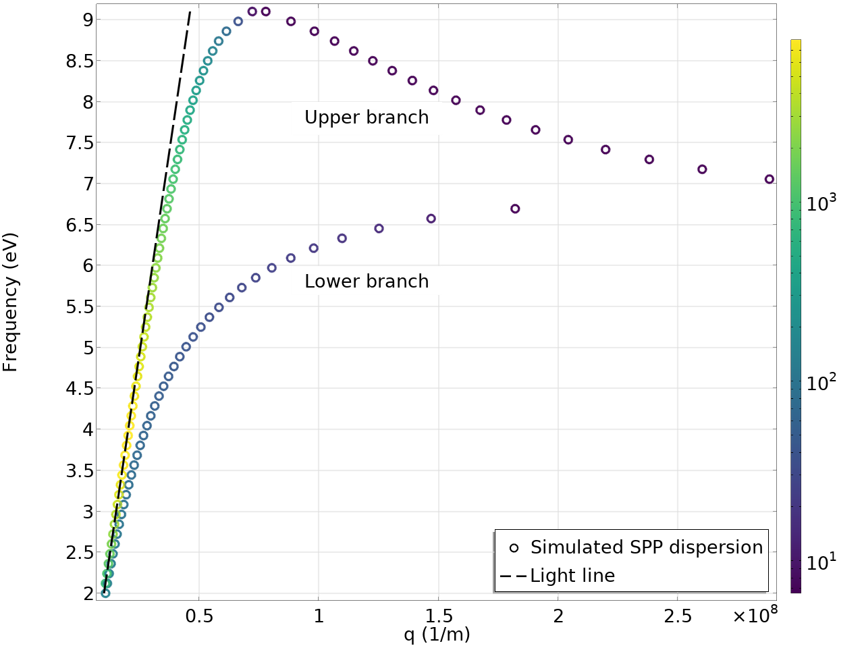
模拟的夹在两个介电薄膜之间的铝薄膜上的表面等离激元色散。两个分支显示了对称（上分支）和反对称（下分支）模式。

虽然在这里没有展示，但我们可以通过仔细匹配每个接口的边界条件来分析推导出这种系统中的表面等离激元色散。随着系统的几何形状变得更加复杂，推导很快就会变得繁琐。使用 COMSOL^®模拟表面等离激元的优势在于它非常灵活，无论几何组成多么复杂，都可以在软件中计算表面等离激元色散。

新型 2D 材料中的表面等离激元

随着电子行业向小型化发展，2D材料越来越受欢迎。在之前的博客文章中，我们介绍了如何在高频电磁学中对一种2D材料（石墨烯）进行建模。事实证明，2D 材料，如石墨烯，也可以支持表面等离激元。毕竟，具有高导电性的石墨烯表现得像金属。主要区别在于贵金属通常在可见光或紫外范围内具有等离子体频率，这意味着金属在光学频率下支持表面等离激元。另一方面，石墨烯在红外状态下支持表面等离激元，使其成为某些应用独特且有利的材料，例如红外收集和超材料。石墨烯的另一个吸引人的特性是它的导电性可以通过化学掺杂或电调谐来改变。这打开了表面等离激元的可调性，这在传统金属中是无法实现的。

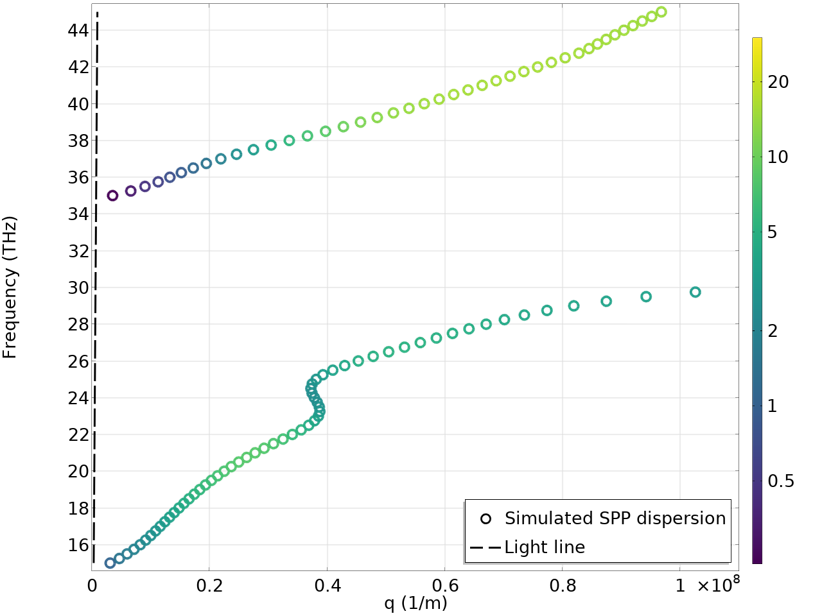
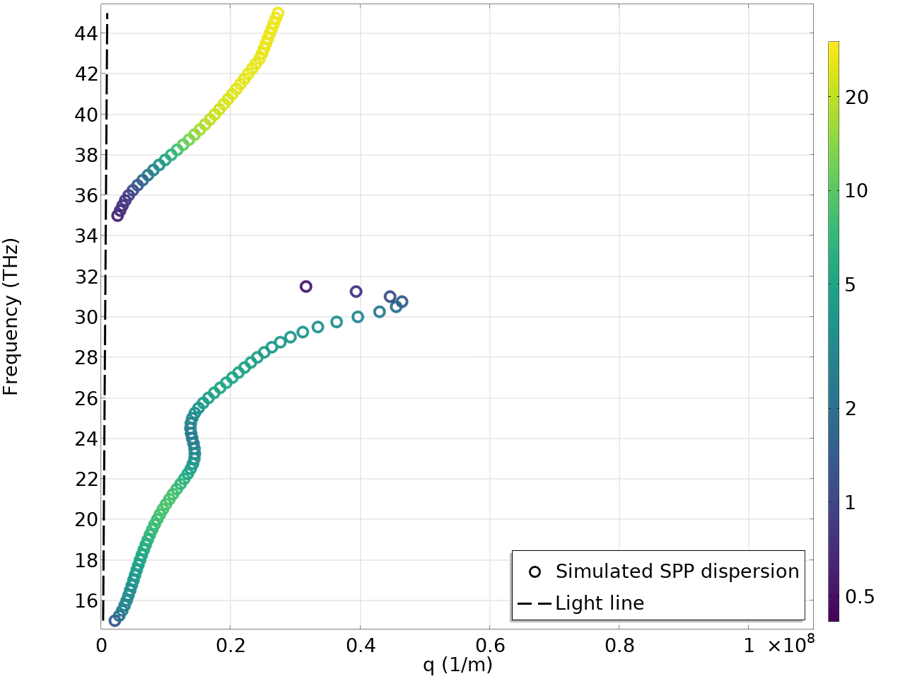
通过模拟表面等离激元传播和色散教学模型，我们可以研究沉积在 SiO₂上的石墨烯中的表面等离激元酶作用物。下图显示了石墨烯费米能量设置为 0.2 eV（左）和 0.5 eV（右）时的色散曲线。由于石墨烯电导率的差异，可以观察到明显的差异。与金属中的表面等离激元色散相比，我们可以看到这里的光线非常陡峭，它几乎与y轴对齐。这是因为表面等离激元传播常数比自由空间光子波数大得多。换句话说，表面等离激元波长要小得多。在下面的动画中，我们可以看到当费米能量设置为 0.2 eV 时，表面等离激元在 29 THz 的传播。此时，自由空间波长约为 10\mum，表面等离激元波长小于 100 nm，实现了神奇的波长压缩！但是，我们确实需要注意，在这种情况下，Q 因子不是很高。等离激元在传播仅几百纳米后就完全衰减了。通过改善石墨烯的晶体质量或将其冷却到低温，可以实现更高的 Q 因子。

费米能量为 0.2 eV（左）和 0.5 eV（右）的石墨烯表面等离激元的色散曲线。

石墨烯表面等离激元在 29 THz 下的传播。石墨烯的费米能量设置为 0.2 eV。

乍一看，在色散图中，在 33 THz 左右的频率范围内没有表面等离激元，这似乎很奇怪。这是由于衬底材料 SiO₂的介电常数，由于其声子共振变为负值。这种情况可以通过绘制 SiO₂的实部来查看模拟频率范围内的介电常数。

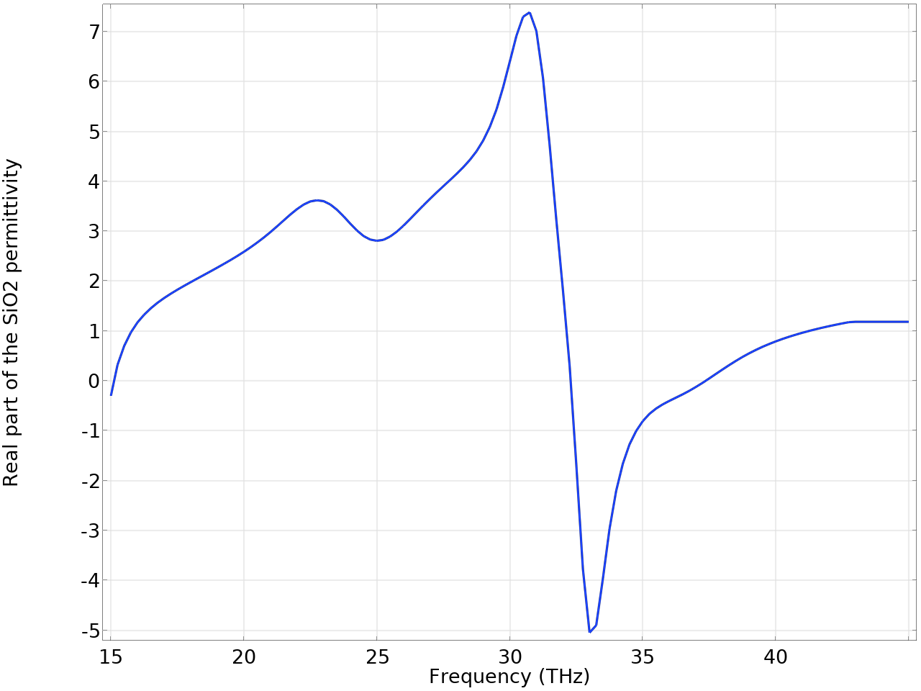
SiO₂的实部红外频率的介电常数。由于声子共振，介电常数在 33 THz 左右变为负，其中石墨烯表面等离激元不受支持。

在本文的前面，我们简要提到了可用于激励表面等离激元的不同实验技术。 仿真提供了激励表面等离激元的替代方法。一个例子是使用电点偶极子源。回想一下，由于波矢量不匹配，表面等离激元 不能被自由空间光激发。然而，点偶极子产生的近场包含具有矢量的分量，这使得表面等离激元被激发。还可以通过执行此类模拟并从场分布中提取表面等离激元波长来绘制表面等离激元色散。下图突出显示了这种类型的仿真，可以观察到清晰的场振荡。

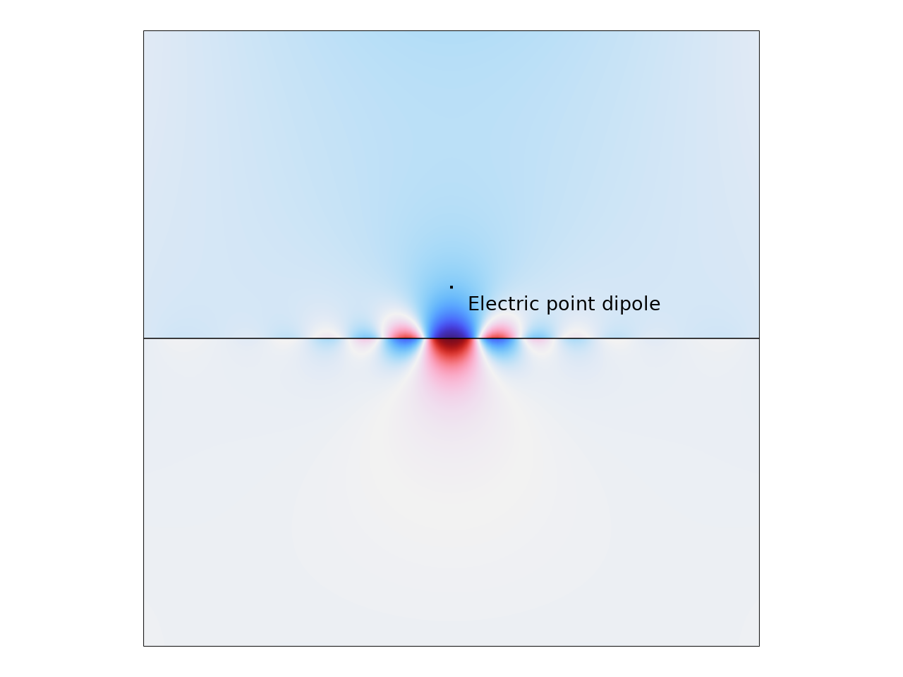
石墨烯表面等离激元被在 y 方向上取向的电点偶极子激励。

结束语

如前所述，表面等离激元只是众多特殊类别的表面波之一。电磁表面波仍在进行深入研究，其可观察到的现象超出了本文的范围。例如，一些各向异性材料，如 MoO₃，可支持单向表面声子偏振子。这是因为在某个频率下，只有一个面内方向的介电常数为负。在下面的动画中，我们可以看到这样的情况，其中SiO₂衬底上的MoO₃板坯由电点偶极子激励。表面声子偏振以表面等离激元特有的“蝴蝶”模式传播，例如石墨烯，其中发射的表面等离激元各向同性地传播。

各向异性表面声子偏振子在 MoO₃中的传播板坯由电点偶极子激励。

通过利用 COMSOL Multiphysics 中的功能，例如电点偶极子节点和边界模式分析研究，我们可以通过多种不同的方式对电磁表面波进行建模，并探索相关的丰富现象。

下一步

单击下面的按钮，进入 COMSOL 案例库，亲自尝试模拟表面等离激元传播和色散教程模型：

参考文献

1. S. A. Maier,Plasmonics: fundamentals and applications. Springer, 2007.