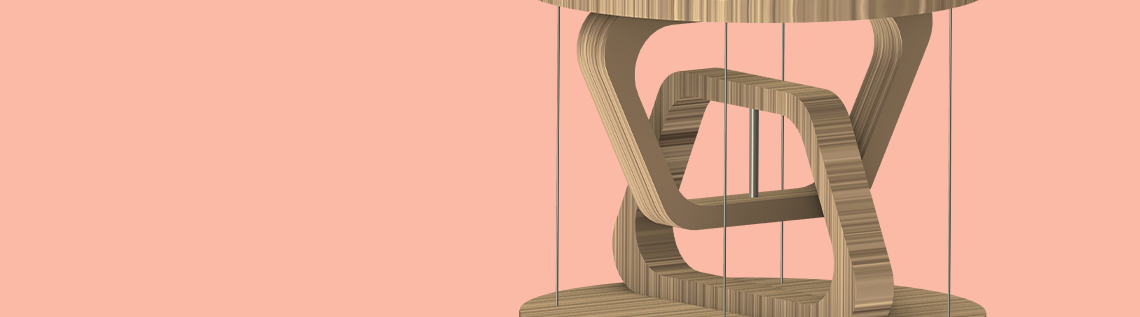
一张桌子可以在不接触地面的情况下保持站立吗?答案是肯定的,张力完整性就可以实现!悬浮桌及其“悬浮的”桌面通过物理的力量,使我们对眼前所看到画面不再怀疑。为了揭示悬浮桌的工作原理,我们先来了解一些其他张拉整体结构,然后再对一个悬浮桌模型展开深入研究。
张力完整性的应用
关于谁最先将张力完整性作为一种结构技术的话题,目前还存在争议,但 “张力完整性”一词由工程师兼建筑师巴克敏斯特·富勒(Buckminster Fuller)在 20 世纪 60 年代首次提出,是“张力的完整性”的简称。张力完整性是基于单个刚性构件(如管或梁)和柔性构件(如电线或电缆)组成的系统建立的结构原理。刚性构件处于持续压缩状态,它们不是通过互相接触连接,而是被处于持续拉伸状态的柔性构件固定在一起,形成一种能够自我支撑的内部稳定性结构,从而无需预期的必要条件,如地基、连接件或支柱。由于张力完整性具有相互关联的性质,因此每一部分对更大的整体功能都至关重要。
在土木工程人员利用张力完整性建造像多面穹顶这样的建筑结构之前,这一原理可以在自行车轮胎这样的简单结构,甚至自然界(如蜘蛛网)中看到。

张拉整体结构使用的材料少,因此质量轻、适应性强,在环境友好型建筑设计中有应用潜力。尽管如此,工程师们暂时还没有将张拉整体结构用于住宅等民用建筑,因为张拉结构难以抵抗地震破坏等。如今,张拉整体结构通常作为一种辅助手段使用,例如德国慕尼黑奥林匹克体育场,它本身并没有采用张拉整体结构,但屋顶采用了这种技术。钢缆和丙烯酸玻璃通过张力完整性被固定在一起,形成了美观的网状结构,可以抵御风雪。

德国慕尼黑奥林匹克体育场,屋顶采用了张力完整性技术。获Creative CommonsAttribution-Share Alike 3.0 Unported许可,通过Wikimedia Commons共享。
为了进一步展示张拉整体结构的功能,我们再来看两个例子。
塔楼和机器人
在华盛顿特区的赫希洪博物馆(Hirshhorn Museum)外,有一座 60 英尺(约 18 m)高的钢铝雕塑,与地面只有14 英寸的接触(约 35 cm),艺术家肯尼思·斯内尔森(Kenneth Snelson,富勒的学生)将其命名为“针塔”,由于它能够利用张力保持直立,斯内尔森称之为 “悬浮压缩”(Floating Compression)。

华盛顿特区赫希洪博物馆外肯尼思·斯内尔森的针塔(1968 年)。获Creative CommonsAttribution 3.0 Unported许可,通过Wikimedia Commons共享。
从美国国家航空航天博物馆出来的游客会经过一座“针塔”,在那里他们可能会了解到另一种已建成的张拉整体结构:NASA 超级球机器人。
超级球机器人是美国国家航空航天局(NASA)为行星着陆和探索设计的机器人原型,它基于张力完整性原理工作。该机器人由缆线和杆组成,通过改变缆线的长度和拉力,机器人可以向任何方向移动,从而拉动杆使机器人可以穿越不可预知的地形。这种结构的弹性可以吸收撞击力,使其无需安全气囊就能掉落在地面上。

NASA的超级球机器人。获Creative CommonsAttribution-Share Alike 4.0 International许可,通过Wikimedia Commons共享。
虽然这些例子都令人赞叹,但张拉整体结构并不一定要涉及 60 英尺高的雕塑和星际探索机器人。张力完整性的基本原理简单易懂,您甚至可以在自己家里做一个张拉整体结构的实例!张力桌,或称为 “悬浮桌”,是张力完整性原理最基本的应用:一个固定部件在张力的作用下被一个柔性部件托起。为了展示悬浮桌的工作原理,我们使用 COMSOL Multiphysics®软件制作了一个模型,该软件可以分析作用在保持张力的导线上的应力。接下来,让我们来看看是什么让这张桌子浮起来的!
悬浮桌的构成
最简单的悬浮桌由两块刚体组成:上半部分(桌面和一条向下延伸的弯曲桌腿)和下半部分(桌底和一条向上延伸的桌腿)。两条腿之间用一根金属丝连接,这样当重力将上半部分向下拉时,金属丝的张力可以防止上半部分掉落地面。
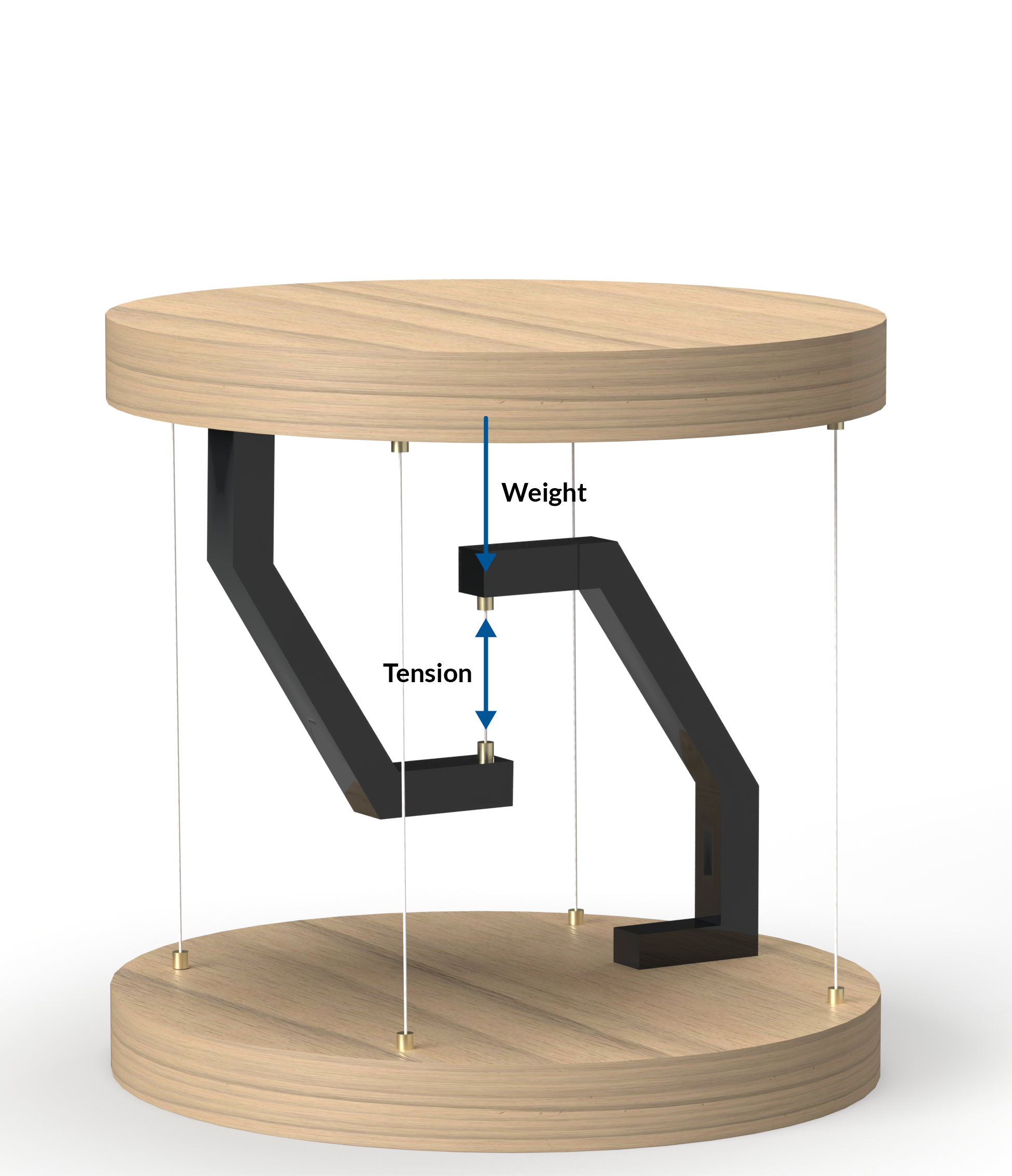
悬浮桌中的张力可以抵消重力。
虽然一根中心线就可以将上半部分悬挂在桌子的下半部分,但为了防止桌面倾倒,还需要有几条支撑线将桌面边缘与底座边缘连接起来。当桌面的重量均匀分布时,这些支撑线的张力通常很小。如果在桌面的一边放置一个物体,就会对该区域施加了较大的向下力,对面桌边的钢丝就会承受较大的拉力,来保持桌面水平。
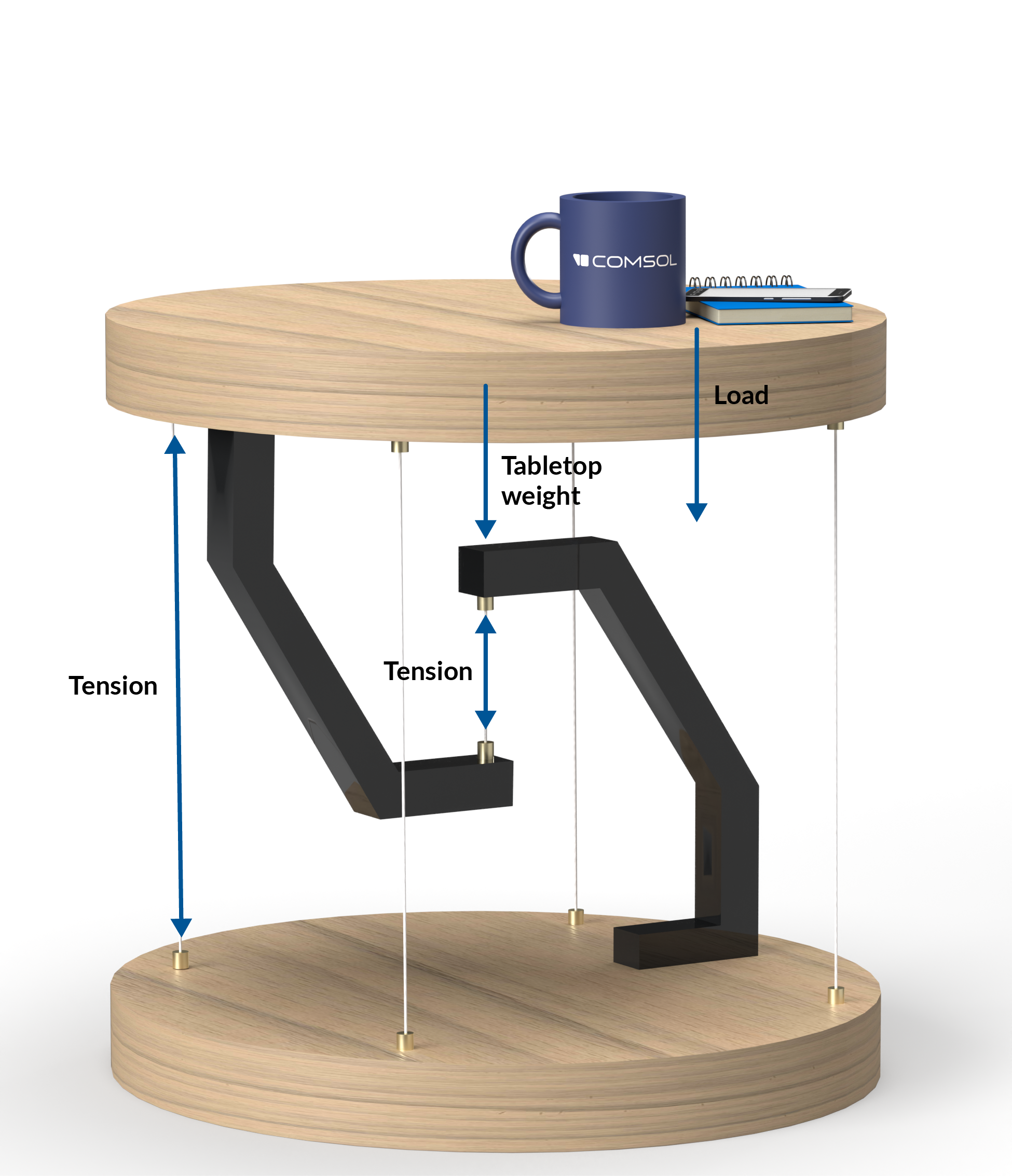
用于稳定悬浮桌的外部钢丝线。

用于平衡上部分的所有力都已标出。
有趣的事实:悬浮桌(如上图所示)的设计通常是对称的,因此可以将其翻转过来用,其工作原理仍然相同。
模拟张力完整性
示例模型中的悬浮桌由密度为 500 kg/m3的木材制成。该材料被视为刚性材料。单根中心线和四根外线由钢丝制成。本例中的桌腿相互交错,但并不接触,仅由穿过中心的金属丝固定在一起。

悬浮桌的几何结构。
除了桌子本身的自重载荷外,该模型还分析了两种载荷情况。第一种情况是在桌面上施加不同大小的垂直向下的载荷。第二种情况是施加一个扭转力矩,就好比使桌面像瓶盖一样旋转而在导线中产生拉力。这两种情况都是使用线缆接口对施加的载荷和桌面重量进行模拟,该接口提供了分析线缆系统的功能,既可以单独分析,也可以与其他类型的结构耦合分析。
垂直载荷
第一个载荷为一个垂直向下的压缩力,大小在 0 到 500 N 之间,均匀地被施加在桌面上。中心导线承受载荷,而外侧导线的受力水平为零。除非桌面发生某种倾斜,否则周围的导线将继续保持几乎没有张力的状态。

悬浮桌上的垂直荷载。
扭矩
第二种情况,施加一个 10 N/m 的扭矩。与上一种情况一样,所施加的载荷以及桌子的重量由中心线支撑。由于增加了扭转力矩,而不是直接向下的力,因此外侧弦线也处于拉伸状态,尽管拉伸程度很低。
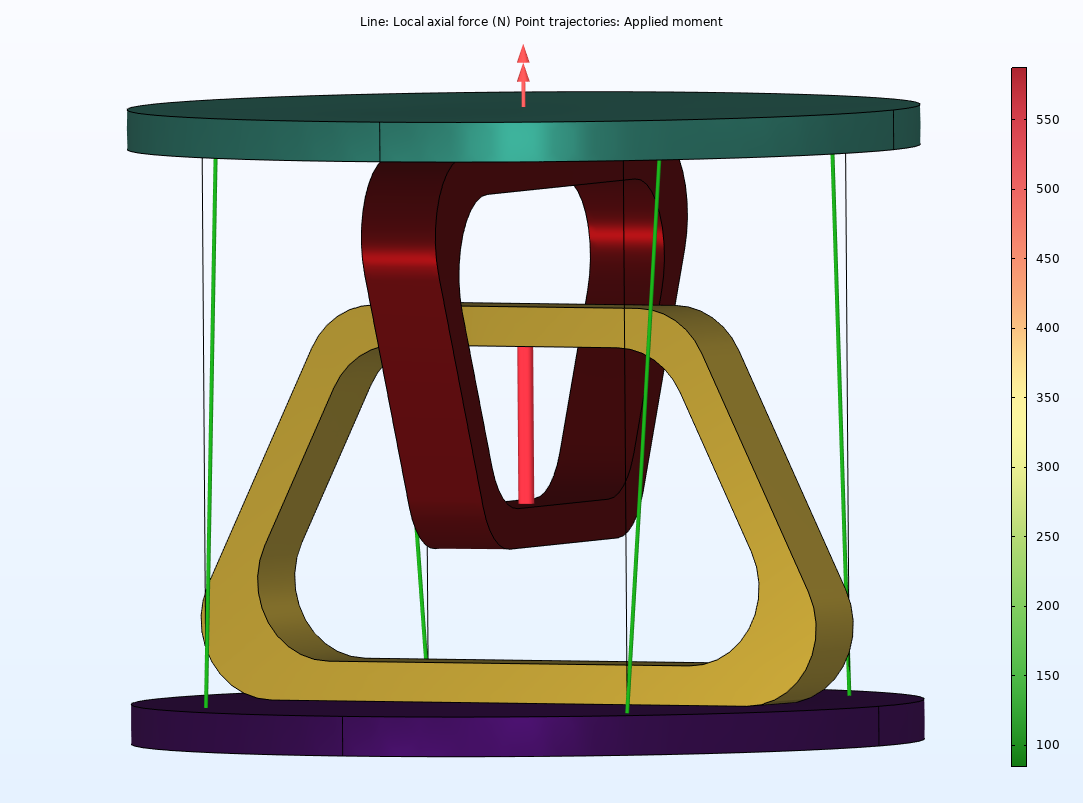
悬浮桌上的扭矩。
张力完整性的未来应用
既然我们已经看到了张力完整性的最简单形式之一,并理解了其基本原理,就有可能模拟更复杂的结构。张力完整性的复杂应用存在于各种事物中,如体育场、雕塑,甚至是行星探测机器人。展望未来,建筑师和工程师们正在寻找更新、更大的张力完整性应用,例如张力摩天大楼。他们希望张力完整性能提供一种适应性强、坚固耐用、同时使用更少轻质材料的建筑技术,从而提出一种生态友好型建筑方案。在这个愿望实现之前,你可以在自己家客厅里摆上一张个人悬浮桌,享受张力完整性技术带来的乐趣!
下一步
- 从COMSOL案例库中下载张拉整体桌的模型文件
- 参阅下列教程模型,尝试在 COMSOL Multiphysics®中分析电缆和电线系统的功能:



评论 (0)