
优化是深入了解模型的有效方法。就像五颜六色的花束中的不同花朵一样,我们可以使用优化模块执行各种不同的优化项目。参数估计也是一种广泛使用的技术。这种分析通常设置为基于测量数据的最小二乘问题,但要获得清晰和唯一的答案,可能需要多次测量。今天,我们来学习如何使用多参数数据集估计参数。
使用多个数据集
在实验室进行实验时,我们的数据依赖于经常使用的测量设备的精确度和准确度。虽然设备的规格中提供了大量信息,但它通常适用于新的、经过良好校准的系统。然而,有时我们可能会忘记校准设备,或者设备系统会因磨损和其他过程而显示出系统性偏差。
如果我们的数据集出现此类错误,那么就需要纠正它们,以便可以准确地分析测量数据。一个应用示例是流经色谱柱的实验,向色谱柱中注入化学物质并记录出口处的穿透曲线。为了进一步分析,使用泵的设定流速。然而,由于钙化,流速系统性地存在偏差。这时,使用各种流速执行多参数优化,就可以获得校正所有数据的因子。
传输问题的多参数优化
这里讨论的优化问题是一个基于使用 COMSOL Multiphysics®软件和稀物质传递接口建立的瞬态模型。完整的模型是优化步骤的先决条件。模型设置为一维,它的几何形状为 1 米长的圆柱。
对于传输属性,我们可以设置流速,即流速乘以柱子的开口宽度。此外,我们可以在入口处指定流入和流出边界条件以及狄利克雷边边界条件,并将其设置为固定浓度。
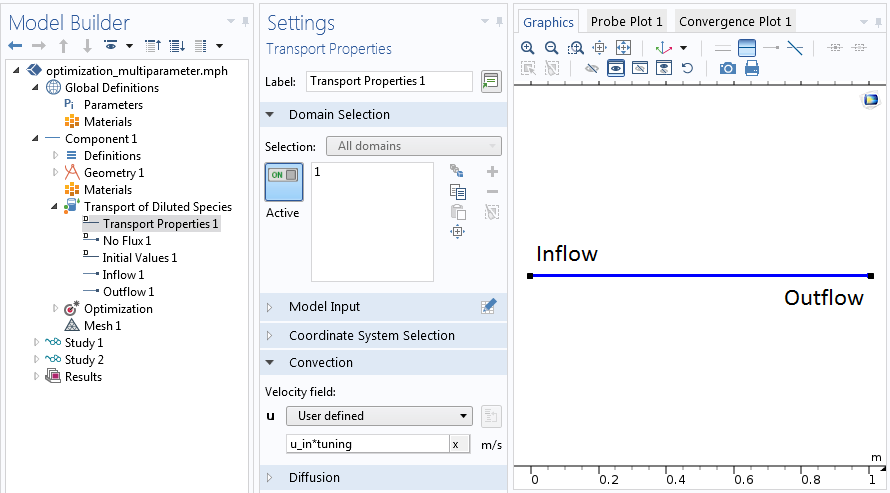
在优化之前设置物理场问题。
虽然这个问题本身的真实速度不知道,但是我们可以把它重新写为实际产物的速度u_in*tuning。在这里,u_in表示设定的流量和全局校正因子的调节,它直接来自u_in=Q/(A*tuning)。因此,校正也考虑了系统的面积变化。
在优化术语中,u_in是识别单个实验运行的实验参数。调节是控制变量,获得的浓度是我们的最小二乘目标,将其与测量数据进行比较。
设置优化
从完整的物理模型开始,我们可以添加两个项目将其转换为优化模型。首先,示例中的优化接口有两个节点:目标和控制变量。对于任何优化研究,这些节点都是先决条件。
虽然有许多可行的优化目标,但最小二乘目标是明确定义的,并且来自形状Sum_i(u_obs_i-u_sim_i)2。因此,它最小化了所有给定数据点之间的距离总和。
由于采用了严格的形式化方法,所以我们不需要表达目标函数。但是,我们需要一个包含最小二乘目标所需的所有信息的数据文件。需要注意的是,数据文件需要按列进行结构化。我们可以在子节点中分配各个列。
请注意,模型开发器树中节点的顺序(从上到下)对应于数据文件中的列顺序(从左到右)。当然,数据文件的每一列都被适当的子节点标识也同样重要。
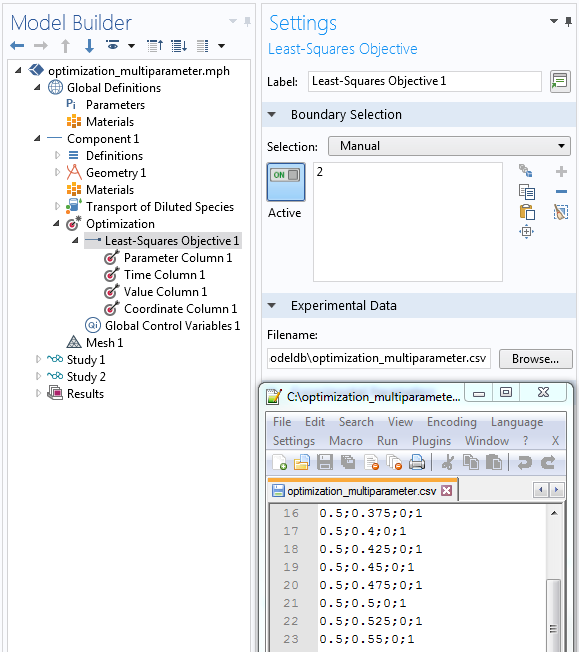
将最小二乘目标(自上而下)中的节点分配给数据文件中以分号分隔的列(从左到右)。
传输优化示例需要四列:
参数列
在示例中,我们在参数列中设置了标识符u_in。这是用于区分不同实验以及在全局定义>参数下分配的相同参数的泵流量。我们还可以在稀物质传递接口中找到用于传递属性的此参数。
时间列
数据文件中规定的时间需要以国际单位制秒为单位。但是,一般来说,这些时间不需要与存储的输出时间精确匹配。尽管如此,仍然建议使用良好的精度。
值列
在值列中,给出表达式,这个表达式根据数值模型结果进行评估。这应该以代表记录数据的精确度量的方式输入。变量名指的是测量数据,在后处理过程中可以使用这样的名称来访问。
坐标列
文件中规定的坐标是进行测量的目的地。还有一个必须考虑的特性:数据文件中的坐标列数量必须与几何的维度相同,即使所选的最小二乘目标特征位于较低的维度上。在这种情况下,模型表达式会在给定选择的最近点处进行评估。
添加优化研究节点
在这里,我们通过将方法设置为著名的 Levenberg-Marquardt 算法来进行两次调整,这个算法目的是有效地解决最小二乘问题。由于目标是执行多参数研究,我们可以将最小二乘时间/参数方法切换为:来自最小二乘目标。其他设置暂时可以保留为默认值。
正确的时间步进和参数扫描可以直接从数据文件中识别,无需在步骤1:瞬态设置。最终,使用这样的设置,求解器可以对所有时间步长和参数的所有平方偏差进行求和,并通过找到适合所有单个实验的全局校正因子来搜索和最小化此类总和。
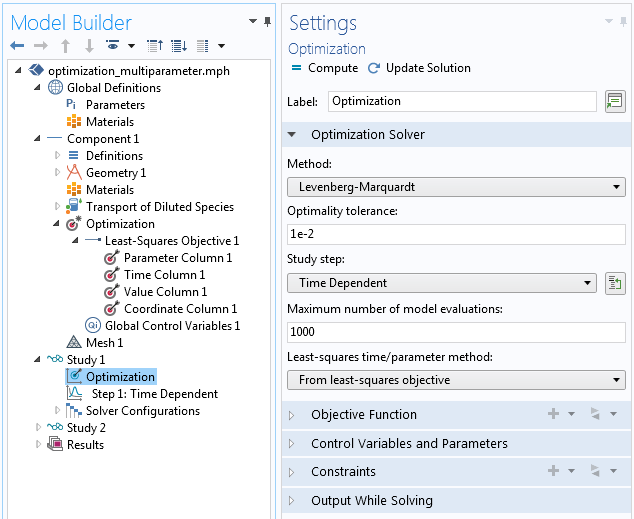
优化研究步骤的设置。
结论
完成所有这些设置,我们就拥有了一个非常通用的模型,只需要更新底层数据文件就可以将它应用在许多实验中运行。这些设置会根据实验参数自动调整模型,包括实验参数记录的采样时间数量的变化。
使用这样的模型可以很容易地扩展到考虑更多的参数变化;例如,以模拟方式输入浓度或更多测量位置的变化。可以使用进一步的步骤将模型转换为应用程序,我们可以在其中自由选择柱的长度,从而选择几何形状。这样,我们最终将获得一个强大的工具来评估我们的实验并确保数据准确。
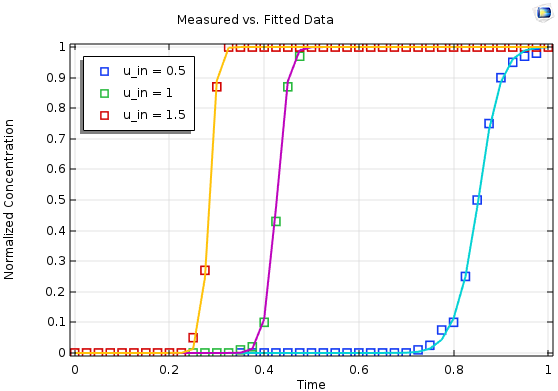
基于三个单独测量值(符号)与模拟和优化输出(线)的多参数拟合结果。
拓展阅读
- 尝试建立液相色谱教学模型:
- 阅读下面这篇相关的博文,了解更过信息:



评论 (0)