最新内容

热粘性声学的理论基础:热损耗与粘性损耗
2014年 2月 27日
当声音在尺寸狭小的建筑和几何结构内传播时,热损耗和粘性损耗会导致声波衰减。具体来说,损耗发生在近壁的声-热边界层与粘性边界层中。为了建立与实验测量结果精确匹配的模型,我们需要考虑这一已知现象,并评估这些损耗对热粘性声学系统造成的影响。

分布式内存计算入门:定义、目的及原理
2014年 2月 20日
在“混合建模”系列的上一篇文章中,我们讨论了有关共享内存计算的基础知识:什么是共享内存、为什么使用共享内存,以及 COMSOL 软件如何在计算中利用共享内存。今天,我们将讨论混合并行计算的另一个组成分支:分布式内存计算。
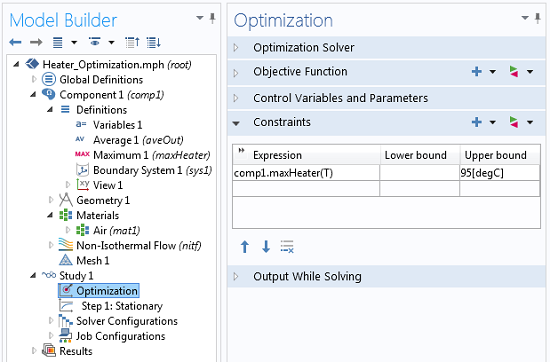
优化加热器功率
2014年 2月 17日
我们展示了一种使用 COMSOL Multiphysics® 和优化模块进行过程控制建模和优化的有用方法。

压电材料的晶体取向和极化方向
2014年 2月 14日
正压电效应和逆压电效应与材料的各向异性程度密切相关,反过来,各向异性又受压电材料的晶体结构影响,同时各向异性的程度还受 极化 过程的影响。这篇博客,我们将介绍如何在 COMSOL 软件中正确地模拟压电材料的晶体取向和极化方向。
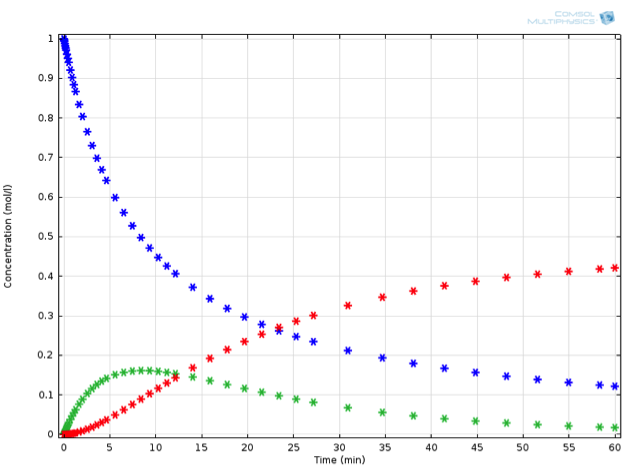
用阿伦尼乌斯方程描述化学反应动力学
2014年 2月 13日
无数的复杂情况和陷阱使化学模拟具有挑战性。在这篇博客中,我们对化学动力学和阿伦尼乌斯定律进行了介绍,以提供帮助。

使用投影算子分析仿真结果
2014年 2月 12日
还记得用手在墙上制作皮影戏吗?投影算子,可以用类似的方法分析你的仿真。让我们来解释一下…
使用组件耦合功能模拟温度控制器
2014年 2月 11日
了解如何在 COMSOL Multiphysics® 的热过程模拟中实现一个简单的温度控制器(反馈回路)。我们以硅晶片为例进行演示。
如何选择正确的电流分布接口?
2014年 2月 10日
在设计电化学电池时,我们需要考虑电解质和电极中的三类电流分布:一次分布、二次分布 和三次分布。不久之前,我们介绍了电流分布的基本理论;本文则以线电极为例,详细解释不同的电流分布类型,帮助你在 COMSOL Multiphysics 中选择合适的电流分布接口,顺利执行电化学电池仿真。
