搜索结果

求解非线性稳态有限元问题
本篇博客中,我们将简要介绍求解非线性稳态有限元问题的算法,并通过一个非常简单的一维有限元问题来演示这些内容,即我们在“求解线性稳态有限元模型”博客中所讨论的那个问题。

求解线性稳态有限元模型
本篇博客是求解器系列的首篇博客,将介绍用于求解所有线性稳态有限元问题的算法。虽然我们在博客中基于一维有限元问题进行介绍,但所讲解的内容具有普适性,能帮助您理解博客系列中接下来将介绍的更加复杂的非线性多物理场的求解技巧。
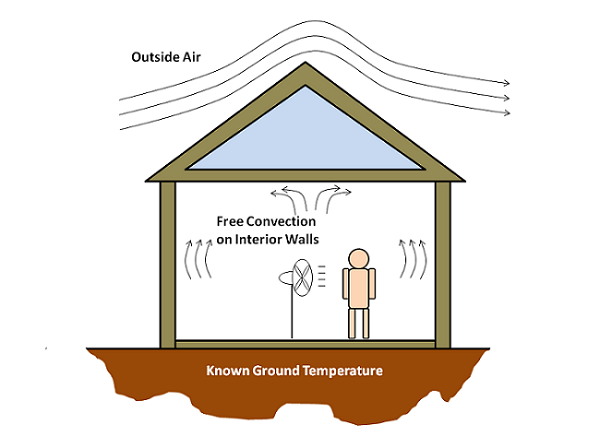
使用全局方程模拟室内空气温度
前些天我遇到了一个有趣的问题,它促发了我想要写一篇博客的灵感,因为它使我想到了我们的 COMSOL Multiphysics 软件中一个非常强大但常常没有得到充分利用的功能:全局方程。
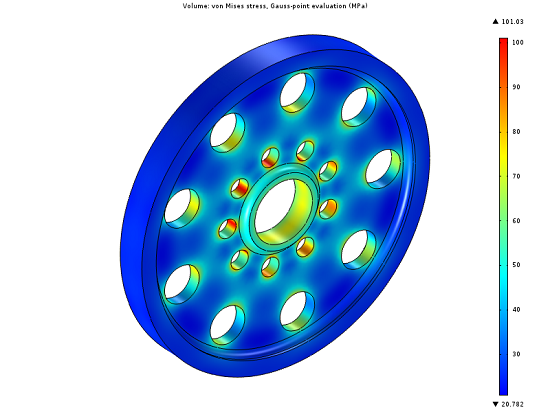
使用无梯度的优化方法求解模型
COMSOL 软件的优化模块包含基于梯度和无梯度的优化 2 种功能。基于梯度的优化方法可以计算目标函数和任何相关约束函数的精确解析导数,但它要求函数是平滑和可微分的。在这篇博客中,我们将研究无梯度优化器的使用,它可以考虑不可微分或不平滑的目标函数和约束条件。为了减轻质量,同时保持对零件峰值应力的约束,我们对旋转轮的尺寸进行了优化。 旋转轮的压力 旋转的轮子会产生离心应力,从而导致整个零件产生应力。为了减轻质量,轮毂上被切割了一些规则的孔洞。下图中显示了离心力产生的 von Mises 应力。我们希望进一步减轻质量,同时将应力保持在临界值以下。 求解应力 虽然我们可以一次对整个轮子进行建模,但由于这个零件存在镜面对称和旋转对称,因此可以减小模型,从而最大限度地降低计算要求。对称边界条件用于约束该零件。 基于旋转速度、旋转轴和材料密度施加体载荷,用于模拟离心力。该模型使用瞬态求解器求解,即假设转速恒定。 选择设计变量 在这个示例中,假设已经有了一套制造工艺,我们希望对零件的整体设计做最小的改动,以降低重新加工的成本。设计变量的一个常见选择就是改变轮毂上孔的半径。因此,我们回到几何序列,对孔的半径及其位置进行参数化。我们还可以根据纯粹的几何分析推算出,每个孔的最大半径必须有一定的限制,否则孔与孔之间的区域会变得太薄,孔与孔之间就会重叠。我们还将对最小半径设限,因为我们不希望孔洞完全消失。 定义目标函数和约束条件 这里的优化目标只是减少零件的质量,即所有域上材料密度的积分。 优化目标是使质量(密度的积分)最小。 这个约束条件稍微复杂一些;我们希望尽量减小零件的峰值应力。但是,我们并不知道峰值应力会出现在哪里。如果内孔或外孔太小,就会导致孔周围应力集中。如果我们将孔的半径做得过大,孔之间的材料就会变得过薄,同样会导致高应力。因此,我们必须监控整个零件的最大应力,并将其限制在指定的峰值应力以下。这是一种无差别约束,尤其需要使用无梯度优化方法。 峰值应力通过域探针进行监测,并命名为 PeakStress。 峰值应力变量受限于一个上限。 用无梯度优化法求解问题 为了求解优化问题,我们在研究分支下添加了优化 功能。Nelder-Mead 方法是两种无梯度方法之一(另一种是坐标搜索)。无梯度优化算法还允许当几何尺寸变化时重新划分网格。 目标函数和约束条件由模型树中的优化 分支定义。控制变量给定了初始条件,我们指定了上限和下限。优化后的设计有很大不同——质量减少了 20%,同时保持了对峰值应力的限制。

非牛顿流体:倒番茄酱的困惑
如果你喜欢吃番茄酱,那么很有可能你已经体验过我们称之为“要么全有要么全无的番茄酱困境”。想象一下,你伸手去拿一个新的番茄酱玻璃瓶,取下瓶盖,把瓶子倒过来时,然后——“什么都没有发生”。直觉上,我们会摇晃或轻拍瓶子,然后——突然你的食物就完全被涂上了番茄酱(当然,除非你的反应真的很好)。在这篇博客文章中,我们将通过仿真模拟瓶子中的番茄酱的流量来演示倾倒番茄酱时的“全有或全无”效果。 我的番茄酱在哪里? 番茄酱除了是一种特别受欢迎的调味品以外,也是一种非牛顿流体。这是它会出现上述奇怪现象的关键。作为一种非牛顿流体,番茄酱的黏度——以及其流动能力——会随着流体的速度梯度或剪切速率变化。当第一次把番茄酱瓶子倒过来的时候,由于番茄酱的初始黏度很高,很可能你只能得到非常小的流量,如果有的话。好在番茄酱还有一个有趣的剪切稀化特性。当在重力之外施加外力时,增加的剪切力将导致番茄酱的黏度降低,更容易流动。这就是为什么我们有时必须轻拍或摇晃瓶子才能享受番茄酱加薯条。 模拟瓶子中的非牛顿流体流动 为了满足我们的好奇心,以及我们的胃口,并进一步完善我们的番茄酱倾倒技术,我们使用COMSOL Multiphysics 软件和其附加的计算流体力学模块对这个过程进行模拟。在模拟中,我们做了几个简化的假设,包括瓶子的无限延伸(即番茄酱一直都有)和单相层流,忽略了瓶内滞留的空气。所有速度均以米/秒(m/s)为单位。 我们规定了瓶子的几何形状和层流的边界,包括无滑移壁面、压力入口(代表未建模番茄酱部分的重量)和压力出口(外部大气),如下图所示。 用于模拟的二维几何图形。显示了应用的边界条件。 我们还添加了体积力特性,以包括重力和沿着 y 轴摇晃瓶子 0.2 秒所产生的力。 为了给求解器提供一致的初始条件,重力产生的体积力通过阶跃函数从 0 上升到其最大值(过渡区域为 0.05 秒)。摇动动作是以 0.2 秒宽的矩形函数模拟的。在此期间,体积力加倍。 倾倒番茄酱 我们基于Koocheki 等人的工作,我们先做了一个仿真为之后模拟番茄酱的流动做准备。为了模拟番茄酱的流动,我们使用了非牛顿幂律来表示动力黏度。番茄酱配方通过在幂律方程中指定稠度系数和流动特性指数来模拟。下面的图像显示了添加1%黄原胶的番茄酱配方中较高的初始黏度和非牛顿流动性。 左:以p1(见上面的模型设置)为单位测量的黏度是时间的函数,时间间隔 [0,0.1]秒。右图:以p1(见上面的模型设置)为单位测量的黏度是时间的函数,时间间隔为[0.1,2]秒。番茄酱的剪切稀化特性很明显,尤其是在瓶子摇晃的[1,1.2]秒间隔内。黏度降低,从而允许更多的番茄酱流出瓶子。 左:在三个不同时间沿线 1(见上面的模型设置)测量的黏度。右图:平均出口速度与时间的函数关系。可以看出,番茄酱在重力的作用下慢慢开始流动,然后在摇晃瓶子时容易增加。 左:速度幅度动画从 0.05 到 2 秒。右:1.1 秒时的速度大小。 “番茄酱困境” 等待流速的变化对你来说可能很熟悉。一旦流速开始改变,就会快速变化,导致番茄酱泛滥,覆盖在你的食物上。流速顺其自然地增加导致了剪切力增加,进而降低黏度,导致更高的流速。这就是为什么番茄酱最初似乎是静止的,但后来突然又像水一样流动的原因。 番茄酱从瓶子中流出这个特殊的问题比一开始看起来要复杂得多。有许多变量会影响我们体验一个“绝对的” 番茄酱惊喜。如果你有兴趣进一步研究这种效应,建议你使用 COMSOL Multiphysics 和计算流体力学模块进行模拟实验。例如,你可以研究诸如倾斜角度、瓶子里的空气、甚至瓶子的设计等变量是如何影响番茄酱的倾倒体验的。
