最新内容

模拟电感式位置传感器
汽车需要能够适应各种驾驶路况,还要应对诸如温度波动等环境变化。因此,开发出能轻松应对这些条件的零件至关重要。在 COMSOL 用户年会 2014 剑桥站收到的研究报告中,有一份就重点研究了电感式位置传感器的功能。
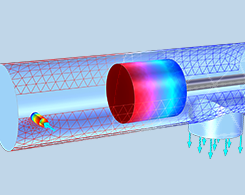
模拟硅基片上的 UHV/CVD 及硅生长
化学气相沉积 (CVD) 能够生产出兼具高质量、高纯度及高强度等优点的材料,因此在半导体行业非常受欢迎。超高真空化学气相沉积 (UHV/CVD) 涉及相当复杂的设备和极高的温度。为了能在提高效率的同时更好地控制成本,工程师们可以对这一复杂工艺进行模拟。本篇博客中,我们将以硅基片的生长为例进行说明。

App 应用程序:改进卡车吊机的额定载重
卡车吊机的设计目的是拖拽各类载荷,在优化吊机的额定载重或者说载重量时,制造人员和工程师们会时刻牢记这一点。利用直观的定制界面,仿真 App 应用程序将仿真的力量带给了那些并非仿真专家的用户,从而加速进行优化过程。我们的卡车吊机分析器 App 显示了这种方法的几大优势。

使用直接流固耦合方法计算声辐射力
本文是上一篇博客的后续报道,我们展示了在 COMSOL Multiphysics® 中计算声辐射力的一种直接的流体-结构相互作用的方法。

创建可调波长 LED 的仿真 App
半导体模块和 App 开发器使定制光电子仿真 App 的开发从未如此简单。在本篇博客中,我们将向您展示如何将 LED 器件的模型转变成一个用户友好的 App,用于评估不同设计对 LED 发射特性和性能的影响。我们还会演示如何使用定制方法来管理结果数据,从而方便地创建定制的分析工具。

如何计算升力和阻力?
在流体流动仿真中,评估流体作用在固体上的力通常很重要,例如作用在汽车或机翼上的升力和阻力。通过计算这些体力,工程师可以量化设计的效率和空气动力学性能。今天,我们将讨论在 COMSOL Multiphysics 中计算升力和阻力的不同方法。

模拟电磁波问题中的金属对象
金属是一种高导电材料,能够非常好地反射入射的电磁波—光、微波及无线电波。当通过 RF 模块和波动光学模块模拟频域电磁波问题时,您可以通过其中的几个选项来模拟金属对象。这里,我们将介绍阻抗、过渡边界条件和完美电导体边界条件,并说明每类条件何时使用。

模拟阀中的堆叠式压电执行器
压电阀的开关由位于密封圈之上的堆叠式压电执行器负责控制。当向堆叠式压电执行器施加一个电压时,它会发生膨胀或收缩,并通过这一变形来打开或关闭阀。本篇博客中,我们将介绍 COMSOL Multiphysics 5.1 版本中新增的一个教程模型,它模拟了气动阀中的堆叠式压电执行器。
借助仿真 App 探索生物传感器设计中的生物学
生物传感器是各类从分子层级理解生物系统详细机制的分析工具的主要部件。这些分析工具可用于各领域的生物分子检测,比如制药、医疗和食物行业、农业、环境技术以及针对生物系统的一般性研究。生物传感器演示 App 是一个非常不错的应用实例,它使得这个领域的人士即使不是仿真专家,也能从精确的多物理场仿真中受益。

LOC 模数微滴分配器的模拟
微流体生物芯片的应用范围很广,同时也因成本低、响应快、效率高而备受业界重视。COMSOL 用户年会 2014 波士顿站收到了一篇名为“芯片实验室应用中高通量微滴分配器的设计与仿真”的论文,其中介绍了研究人员设计的一款带有模数转换器的微流体生物芯片。他们使用 COMSOL Multiphysics 软件来理解器件的工作机理以及验证它的功能。

平行宇宙、薛定谔、霍金、博格斯和单向组合乐队
现在极受欢迎的单向组合乐队(1D乐队)和量子力学、宇宙学之间有什么关系吗?最近在悉尼歌剧院举办的一次演讲中,斯蒂芬·霍金很可能已经对此做出了解释。这涉及对平行宇宙的预测,也就是说,在无限多世界中,可能存在一个与我们完全相同、但存在各种可能的排列与差异的世界,就像是博格斯在 《巴别图书馆》中提到的 410 页的书。

光学介质薄膜的模拟
我们可以通过各类介质薄膜工具控制光的传播。例如,它们可以用作抗反射涂层来减少系统内的杂散光;还可以作为低损耗的反射器或滤波器使用,实现对特定频率辐射的选择性传输。今天的博客将介绍射线光学模块的部分内置功能,可用于模拟包含介质膜的光学系统。

从测量中获取结构力学的材料数据(第二部分)
在本系列的第一篇博客中,我们讨论了将测量材料数据转化为本构模型时的一些注意事项;并详细介绍了超弹性材料。今天,我们将讨论如何使用非线性弹性和弹塑性材料,并将介绍一种您可以直接在 COMSOL Multiphysics 中使用您的测量数据的方法。

如何创建仿真 App:以喇叭天线模型为例
假如能让非专业人士独立运行您的多物理场仿真,您会愿意吗?回答毫无疑问是肯定的,这不仅能节省您的时间,还可以帮助他们便捷地受益于您的专业成果。现在,将仿真转化为简便易用的定制化仿真 App 已经成为了现实。这篇博客文章将解释研发人员为什么应该创建仿真 App 以及如何进行创建,我们将利用新发布的“波纹状圆形喇叭天线模拟器”演示 App 来对此进行展示。

如何模拟三维旋转机械
电动机械是现代工业社会的重要支柱。在这类种类繁多的机械设备中,发电机或电动机一类的旋转机械应用最为广泛。COMSOL Multiphysics 中的旋转机械,磁物理场接口即旨在模拟这些系统。请跟随我们一起探讨旋转机械的模拟过程,并了解使用此功能详细的最佳做法。
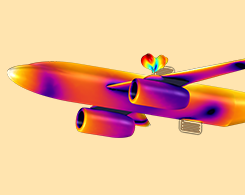
飞机上的天线串扰模拟
航空通信系统变得日益复杂,我们通常需要在同一架飞机上安装多条天线,这样可能会在天线间造成串扰,或称同址干扰,影响飞机运行。“飞机机身上的天线串扰”教学模型模拟了飞机机身上两个完全相同的天线之间的干扰,其中一个负责发射,另一个负责接收,以此来分析串扰的影响。

通过变形实现物理运动的图形化显示
在许多仿真应用中,比如声波、振动机械硬件或管道中的流体,您都会希望能对器件内的运动或变形进行图形化显示。后处理和图形化显示能帮您加深对仿真结果的理解,通过绘图来显示物理运动也能使您综合考虑器件中的每个方面。变形是帮助实现这一点的绝佳方式。

热式质量流量传感器的行为描述
经过多年的发展,传感器技术现在能够更精确地测量流体流动行为。热式质量流量传感器就是这样一类设备。该仪器设计简单、操作方便,而且精度极高,因此很受人们的重视。剑桥大学的研究团队使用 COMSOL Multiphysics 设计了一款热流量传感器三维模型,用于分析这一流动仪零部件中的动力学。

混合动力和电动汽车中的牵引力从何而来?
您可能会认为自己开车很稳,但您的发动机很可能并不这么认为。每天我们都要面临像信号灯这样的路障和变速限制,这意味着我们对汽车动力传动系统的动力需求变化很大。我们希望混合动力或电动汽车的性能可以与现代汽车相提并论,比如当频繁踩油门和刹车的时候。所以,设计人员需要能以一种安全的方式实现这类目标,这其中就涉及了对电池的模拟。

仿真助力评估超高频 RFID 标签设计
COMSOL Multiphysics 5.1 版本引入了新的超高频 RFID 标签教程模型。RFID 标签使您可以通过使用电磁场来识别并监控无生物和生物。超高频 RFID 标签的应用范围大于其他类型的 RFID 标签,常用于动物识别。我们可以通过分析电场与远场辐射模式来评估该标签的性能。

借助 COMSOL® 仿真 App 执行弱形式
在之前的弱形式系列博客中,我们对弱形式方程进行了离散,希望得到可用于求解我们简单示例问题中未知系数的矩阵方程。按照博客“在 COMSOL Multiphysics 中执行弱形式”中的步骤操作,我们将能在 COMSOL Multiphysics® 软件中执行该方程,并能加入其他步骤来检查矩阵。我们还发现可以借助 COMSOL® App 更轻松地实现所有相关矩阵的同时展示,并能在同一个屏幕上按类排列。

COMSOL Multiphysics 5.1 版本给我们带来哪些新期待?
今天标志着 COMSOL Multiphysics 5.1 版本的正式发布。最新版的 COMSOL 软件中包含 20 个演示 App 应用程序、许多新的特征,以及对现有产品功能的极大提升。这里将向您介绍下载 5.1 版本后能获得哪些新功能。

如何选择 CAD 数据处理模块?
COMSOL Multiphysics® 软件提供了多个附加模块来处理外部 CAD 及 ECAD 数据。这些模块支持在 COMSOL Multiphysics 分析工具与 CAD 和 ECAD 设计软件之间进行单向或双向数据传输。本篇博客将介绍这些模块的功能及其应用的必要性。

借助 Beer-Lambert 定律模拟激光与材料的相互作用
高强度激光入射在部分透明材料上会在材料本身沉积功率。如果能借助 Beer-Lambert 定律描述入射光的吸收,我们就可以通过 COMSOL Multiphysics 的核心功能来模拟能量的沉积。本博客将介绍如何模拟吸收率受温度影响的材料对入射光的吸收,以及随之对材料产生的加热。
