最新内容
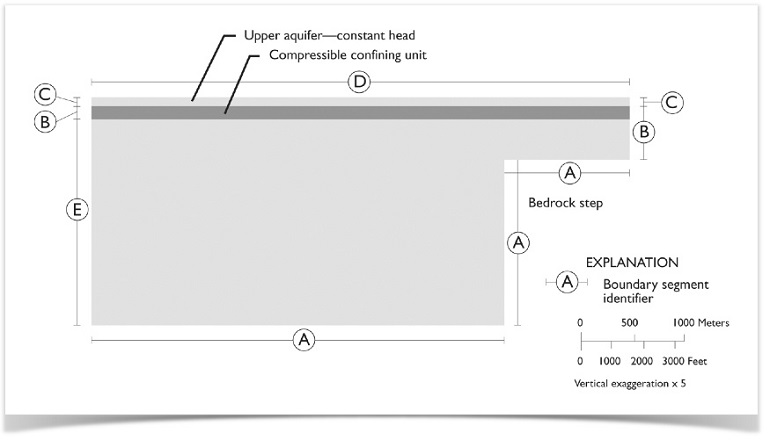
通过多孔弹性分析地基固结
您可以在构建结构之前进行多孔弹性分析,以帮助预测可能由多孔弹性变形引起的沉降。

使用 COMSOL 软件模拟地热过程
这是新的“地热能”系列博客文章的第一篇,我们将介绍模拟地热过程的基本概念以及大量相关的物理现象。我们还将向您展示一个地埋管换热器的示例模型。

借助 COMSOL API for use with Java® 实现建模任务的自动化操作
如今新产品的研发周期越来越短,为了在市场竞争中抢占先机,研发工程师和科学家们需要一件高效的工具,来帮助他们最快地获取计算结果,并摆脱重复性的例行工作。COMSOL Multiphysics® 正是他们需要的!COMSOL 软件拥有参数化扫描等多种内置功能,可帮助用户提高仿真工作效率。除了能够实现图形建模之外,它还拥有应用编程接口(Application Programming Interface,简称 API)。借助 API,用户便能对任意重复的建模步骤实现自动化操作。下面我们来了解一下 COMSOL API for use with Java®。
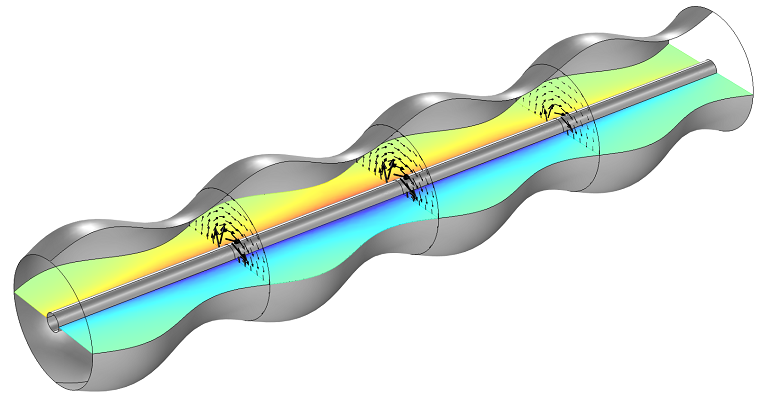
计算波纹波导的阻抗
您知道可以在 COMSOL Multiphysics® 中计算横截面不均匀的波导(如波纹波导)的有效阻抗吗?我们将在这里为您演示。

使用 COMSOL 计算单面磁体产生的力
磁体:它们是如何工作的?您可以使用 COMSOL Multiphysics® 和附加的 AC/DC 模块来计算单面磁体的力。

批处理扫描中任务并行的附加值
到目前为止,我们在混合建模系列博客中还没有详细讨论的一件事是,当向我们的计算中增加更多计算资源时,我们可以期待怎样程度的加速。今天,我们考虑一些解释并行计算局限性的理论研究,并将介绍如何使用 COMSOL 软件的批处理扫描 选项。这是一个内置的、易并行计算功能,可在达到极限时提高性能。 Amdahl 定律和 Gustafson-Barsis 定律 我们之前已经提到过的如何通过增加计算单元来提高速度是基于算法的(在这篇文章中我们将使用术语进程,但添加的计算单元也可以是线程 )。一个严格的串行算法,像计算Fibonacci 数列的元素,完全不能从增加过程中受益,而并行算法,如向量加法,可以利用与向量中的元素一样多的处理器。实际中的大多数算法都介于这两者之间。 为了分析一个算法可能的最大加速,我们将假设它由一小部分完全并行化的代码和一小部分严格串行化的代码组成。我们调用并行代码 \varphi 的分数,其中,\varphi 是介于(包括) 0 和 1 之间的一个数字。这自动意味着我们的算法有一个等于 (1-\varphi) 的串行代码片段。 考虑 P 个活动进程的计算时间 T(P),从 P=1 开始,我们可以使用表达式 T(1) = T(1) \cdot(\varphi + (1-\varphi))。当运行 P 个进程时,代码的串行部分不受影响,但完全并行化的代码的计算速度将提高P倍。因此,P 进程的计算时间为 T(P)=T(1) \cdot (\varphi / P + (1 -\varphi)),加速度为 S(P):=T(1)/T(P)=1/(\varphi/P+(1-\varphi))。 Amdahl 定律 这个表达式是Amdahl 定律的核心。对于不同的值 \varphi 和 P 绘制图 S(P) ,我们现在在下图中看到一些有趣的东西。 为可并行化代码的不同部分增加进程数的加速比。 对于 100% 并行化代码,极限是不存在的。然而,我们发现对于 \varphi<1,渐近极限或理论最大加速比为 S{max}(\varphi):=\lim{P\to \infty} S(P)=1/(1-\varphi)。 对于 95% 并行化的代码,我们发现 S{max}(0.95)=20,即使我们有无限数量的进程,最大加速也是 20 倍。此外,我们有 S{max}(0.9)=10, S{max}(0.75)=4 和 S{max}(0.5)=2。当减少并行化代码的比例时,理论最大加速比会迅速下降。 但不要现在就放弃回家! Gustafson-Barsis 定律 Amdahl 定律没有 考虑到一件事,那就是当我们购买一台速度更快、内存更大的计算机来运行更多进程时,通常不是想更快地计算之前的小模型。相反,我们想要计算新的、更大(更酷)的模型。这就是 Gustafson-Barsis 定律的全部内容。它基于这样一个假设,即我们要计算的问题的规模随着可用进程的数量线性增加。 Amdahl 定律假定问题的大小是固定的。当添加新的处理器时,它们处理的是最初由较少数量的进程处理的部分问题。通过添加越来越多的进程,我们并没有充分利用所添加进程的全部能力,因为最终它们能够处理的问题大小达到了下限。然而,假设问题的大小随着添加的进程数量的增加而增加,那么我们就将所有进程利用到假设的水平,并且执行计算的加速是无限的。 描述这种现象的方程是 S(P)=\phi\cdot P-(1-\phi),这为我们提供了一个更为乐观的结果,即所谓的缩放加速(类似于生产力),如下图所示: 当考虑到工作的规模通常会随着可用进程的数量而增加时,我们的预测就更加乐观了。 通信成本 Gustafson-Barsis 定律意味着,我们拥有的能添加到进程中的资源才能限制我们可以计算的问题的大小。然而,还有其他因素会影响加速。到目前为止,我们在这个系列博客中试图强调的一点是,通信成本较高。但是我们还没有谈到它有多贵,所以让我们看一些例子。 […]
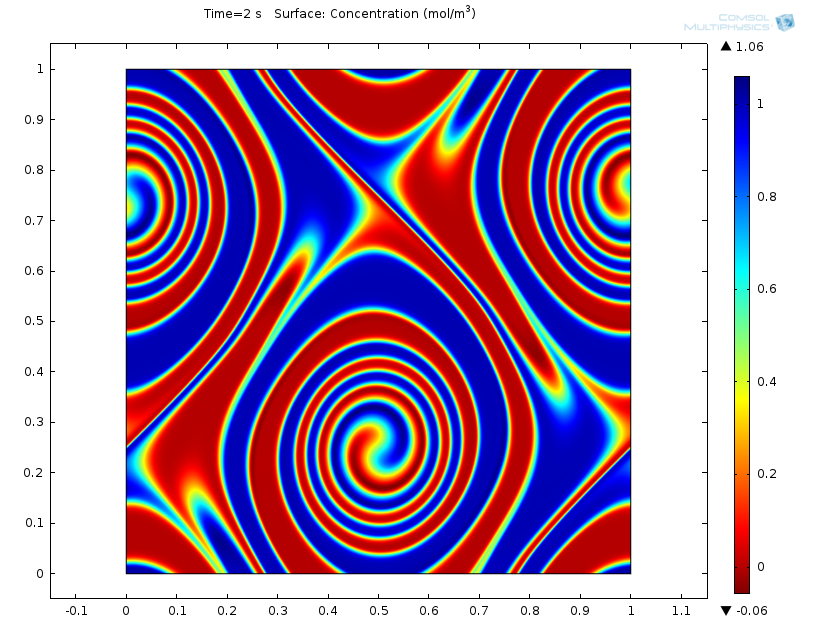
模拟开尔文-亥姆霍兹不稳定性和气候动力学
加热的肥皂泡、波浪状的云和木星大红斑有什么共同之处?它们的形成被称为开尔文-亥姆霍兹不稳定性的不稳定运动。

利用循环对称减少模型计算时间
对于旋转的几何体进行循环对称性简化可能比对轴对称的几何体进行简化更加复杂。了解如何实现这一功能以减少计算内存。

分支线耦合器的建模
分支线耦合器,是一种 90 度 或正交 混合耦合器,由于其制造工艺简单且易于设计,被广泛应用于各个行业。分支线耦合器是无源器件,常用于单天线发射器系统和 I/Q 信号分配器/合路器。让我们了解一下这类耦合器的基本工作原理及一些重要的设计要素。
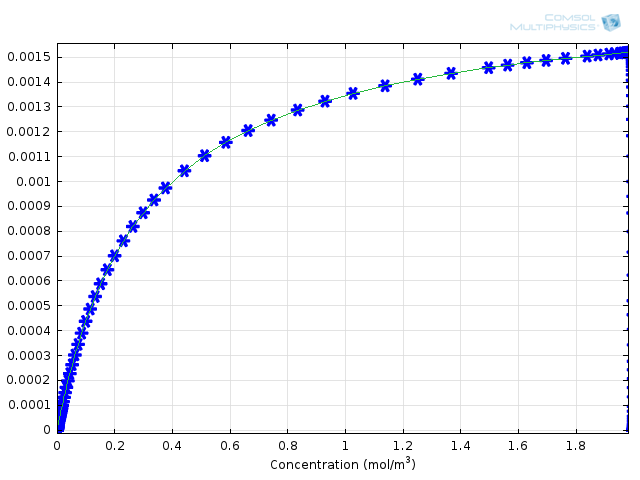
酶动力学,米氏动力学
在 Michaelis–Menten 动力学诞生 100 周年之际,我们以我们所知道的最佳方式–仿真来纪念这一开拓性的成果。

基准模型的结果与菲涅尔方程的解一致
聪明的想法: 当一束光(电磁波)在自由空间中传播时,击中了电介质,一部分光会被透射,一部分会被反射。

COMSOL 中定义材料各向异性的方法
考虑一种碳纤维增强的聚合物,其编织的纤维嵌入环氧树脂基体中。参照众所周知的直角坐标系,你如何表达各向异性的情况?

屈曲,当结构突然坍塌时
解决屈曲问题(如桥梁倒塌或碎苏打罐)的最简单方法是进行线性屈曲分析。在 COMSOL Multiphysics® 中查看如何执行。

混合计算:共享内存与分布式内存相结合的优势
在之前的混合计算系列博客中,我的同事 Pär 介绍了如何在共享内存和分布式内存平台上使用 COMSOL Multiphysics 进行并行数值模拟。今天,我将讨论这两种方法的结合:混合计算。

绘制磁场的空间导数
对于放射学、磁电泳、粒子加速器和地球物理学等领域的应用,计算磁场或磁通量密度的空间导数都很有用。
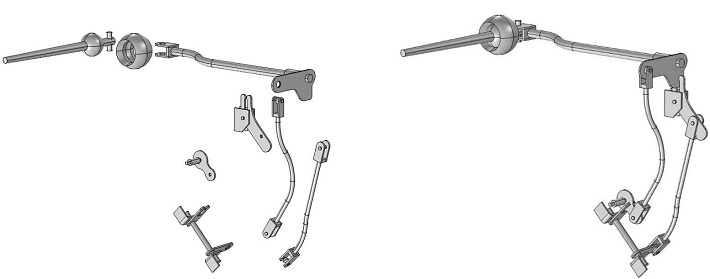
选择第一档:研究老式汽车的换挡原理
跟随我们一起对一辆老爷车的换挡机构进行多体动力学分析。准备上路了吗?
质子交换膜燃料电池建模示例
聚合物电解质膜或质子交换膜(proton exchange membrane,简称 PEM)燃料电池是一种极具应用潜力的便携式清洁电源,是交通运输和发电行业的研究热点。COMSOL Multiphysics,这款强大的仿真工具,可以帮助理解和克服 PEM 电池燃料设计和施工过程中的挑战。

如何在 COMSOL Multiphysics 中模拟热粘性声学
当模拟声学现象、尤其是对几何尺寸非常小的声学装置而言,需要考虑许多复杂因素。热粘性声学 接口为声学模型的建立,及对声压、速度场、温度变化等因素的求解提供了一个简便、精确的方法。在本文中,我们将介绍如何在 COMSOL Multiphysics 中模拟热粘性声学问题,同时还为您提供了一些操作技巧和有用的资源。

热粘性声学的理论基础:热损耗与粘性损耗
当声音在尺寸狭小的建筑和几何结构内传播时,热损耗和粘性损耗会导致声波衰减。具体来说,损耗发生在近壁的声-热边界层与粘性边界层中。为了建立与实验测量结果精确匹配的模型,我们需要考虑这一已知现象,并评估这些损耗对热粘性声学系统造成的影响。

分布式内存计算入门:定义、目的及原理
在“混合建模”系列的上一篇文章中,我们讨论了有关共享内存计算的基础知识:什么是共享内存、为什么使用共享内存,以及 COMSOL 软件如何在计算中利用共享内存。今天,我们将讨论混合并行计算的另一个组成分支:分布式内存计算。
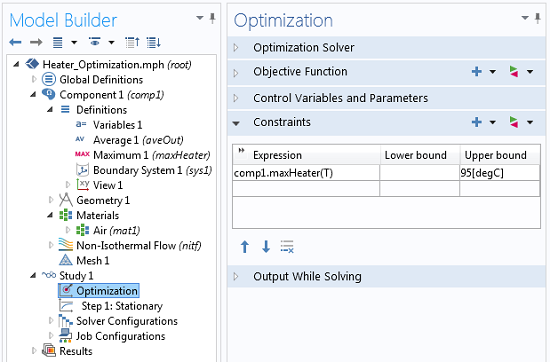
优化加热器功率
我们展示了一种使用 COMSOL Multiphysics® 和优化模块进行过程控制建模和优化的有用方法。

压电材料的晶体取向和极化方向
正压电效应和逆压电效应与材料的各向异性程度密切相关,反过来,各向异性又受压电材料的晶体结构影响,同时各向异性的程度还受 极化 过程的影响。这篇博客,我们将介绍如何在 COMSOL 软件中正确地模拟压电材料的晶体取向和极化方向。
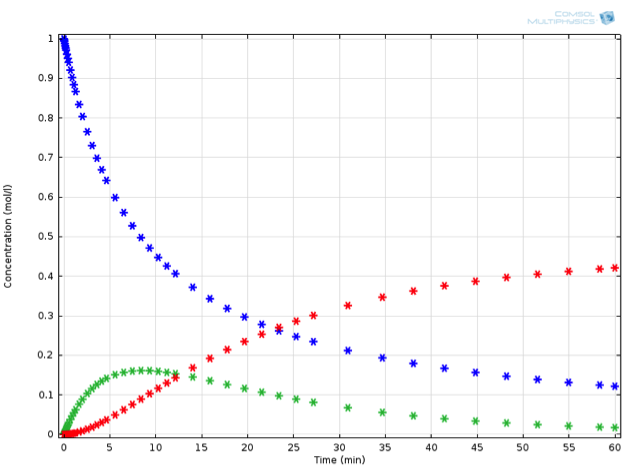
用阿伦尼乌斯方程描述化学反应动力学
无数的复杂情况和陷阱使化学模拟具有挑战性。在这篇博客中,我们对化学动力学和阿伦尼乌斯定律进行了介绍,以提供帮助。

使用投影算子分析仿真结果
还记得用手在墙上制作皮影戏吗?投影算子,可以用类似的方法分析你的仿真。让我们来解释一下…
