
计算磁场或磁通密度场的空间导数对放射学、磁电泳、粒子加速器和地球物理学等领域的应用研究非常有用。其中最重要的一个应用实例就是磁共振成像(MRI)仪的设计,不仅需要分析场强,还需要分析场的空间变化。今天这篇博客将向您介绍如何在 COMSOL Multiphysics®软件中计算和绘制电磁模拟中的磁场梯度。
编者注:本博客于 2020 年 11 月 24 日更新,以反映软件的新增功能和信息。
空间导数:背景和目标
当您在计算由电流引起的磁场、由时变磁场感应的电场或求解 3D 电磁波问题时,对于这三种情况, COMSOL Multiphysics 计算中都会使用旋度(矢量或 Nédélec 边)单元。旋度单元也会被用于涉及面内电流分布的 2D 和 2D 轴对称磁场模拟中。在 AC/DC 模块中,旋度单元通常用于计算磁矢势A,然而,旋度单元不能获得高阶空间导数。
请看博客文章《什么是旋度单元,为什么使用它?》中对旋度单元的详细介绍。
磁通密度B、磁矢势A和磁场H通过磁导率μ相关,如下所示:
这些方程表明,磁通密度和磁场是磁矢势的一阶空间导数的函数。由于没有在旋度单元上定义二阶空间导数,不能直接使用微分算子(d(f,x))得出B和H的梯度。
为了计算二阶空间导数,通常将在旋度单元上定义的B或H场映射到由拉格朗日单元表示的场。COMSOL Multiphysics 5.6 版中引入了laginterp(order, expr)算子,可以更加方便的进行这项操作。这个算子将一个表达式映射到一个指定阶数的拉格朗日场,然后在每个网格单元中对该场进行求值。
当求解涉及面外电流的 2D 或 2D 轴对称磁场问题,或模型内没有任何电流流动的静态磁场问题时,使用拉格朗日单元来求解控制方程,从而可获得二阶空间导数。本博客所展示的方法仅适用于使用旋度单元计算场的情况。
当使用磁场、仅电流接口以拉格朗日单元作为因变量的形函数(从 COMSOL 5.6 版本开始提供)求解磁场时,可以直接使用
d(f,x)算子。
案例:亥姆霍兹线圈
让我们来看一个例子,演示上文介绍的微分算子的用法。我们将介绍如何计算并绘制一个亥姆霍兹线圈产生的磁通密度的空间导数。这个模型的详细描述,以及模拟线圈的步骤说明,可以在COMSOL 案例下载页面中找到。
亥姆霍兹线圈是一对平行的圆形线圈,它们之间的距离等于一个线圈的半径,通过两个线圈的电流流向相同。这种配置常被用于抵消地球的磁场和为实验提供可控的磁场。亥姆霍兹线圈的几何形状如下图所示。在这个模型中,每个线圈匝数为 10,并有 0.25mA 的电流在其中循环。
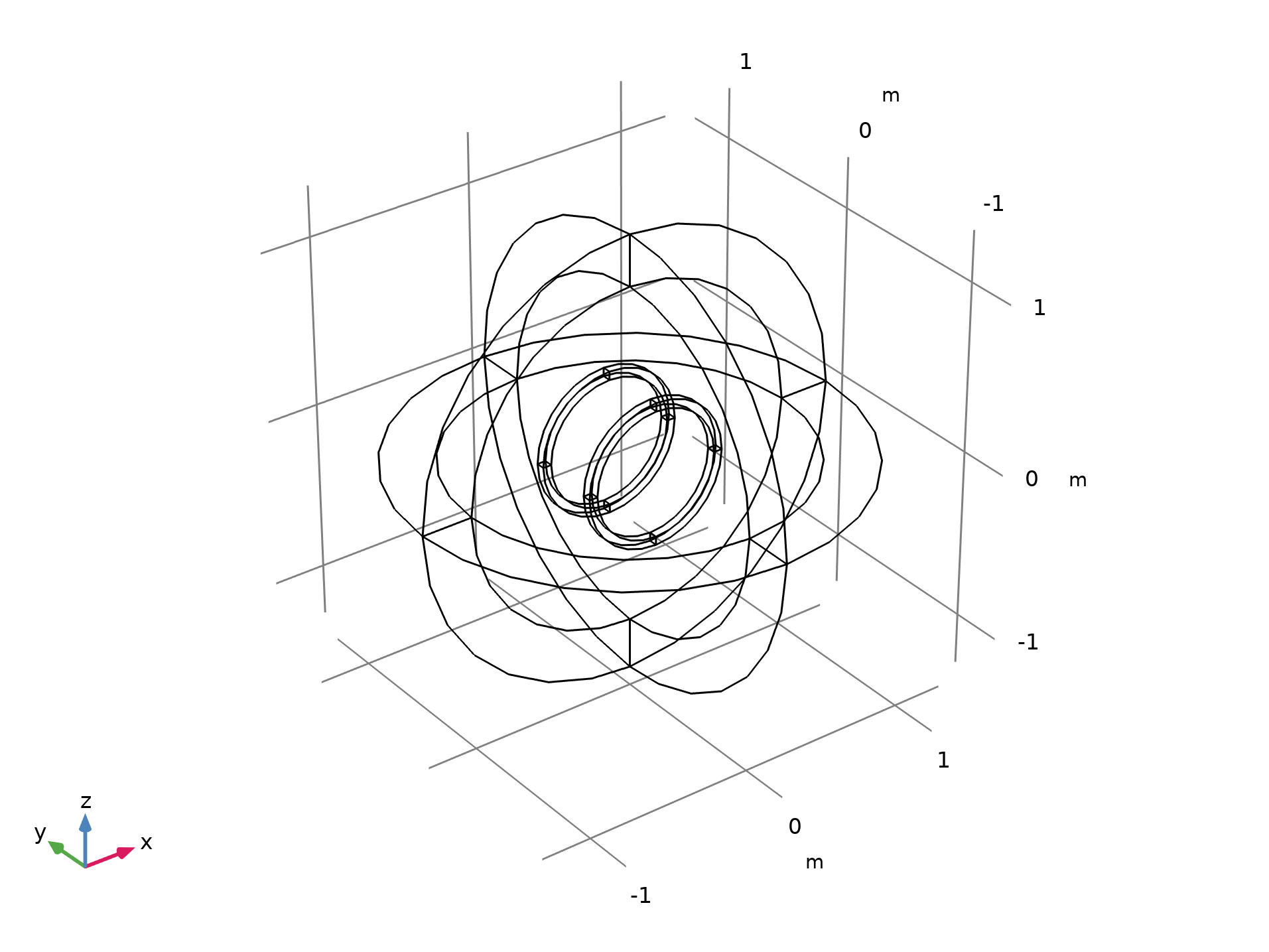
亥姆霍兹线圈的几何形状。最外层的球壳区域是用无限元模拟的。
这个模型演示了使用两种不同的方法来计算磁通密度和它的空间导数。第一种方法是使用磁场物理接口和线圈功能来建立两个线圈的模型。磁场接口使用旋度单元来定义和表示3D的磁通密度。例如,为了计算磁通密度(Byy)的y 分量梯度,我们使用了表达式d(laginterp(2,mf.By),y)。
第二种方法是使用磁场、仅电流物理接口建模,因为模型中没有磁性材料。使用导体功能模拟线圈。由于这个接口使用拉格朗日形函数,我们可以使用表达式d(mfco.By,y)来计算Byy。沿亥姆霍兹线圈中心线的By和Byy的比较见下图。可以看出,每个网格单元中的Byy值是恒定的,因为两个接口都使用了二次单元的离散化来表示磁矢量势A。
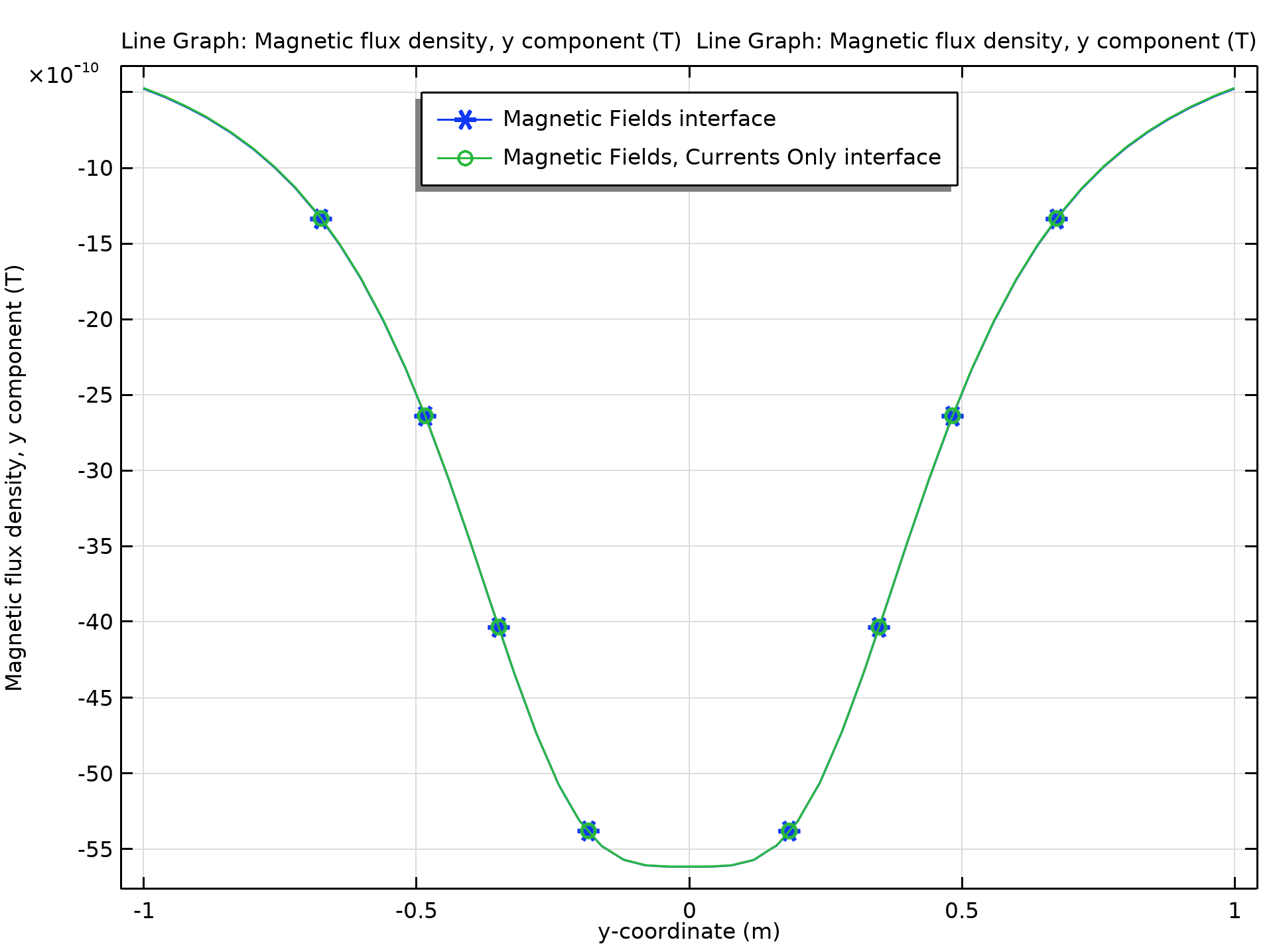
沿亥姆霍兹线圈中心线的磁通密度的y 分量。
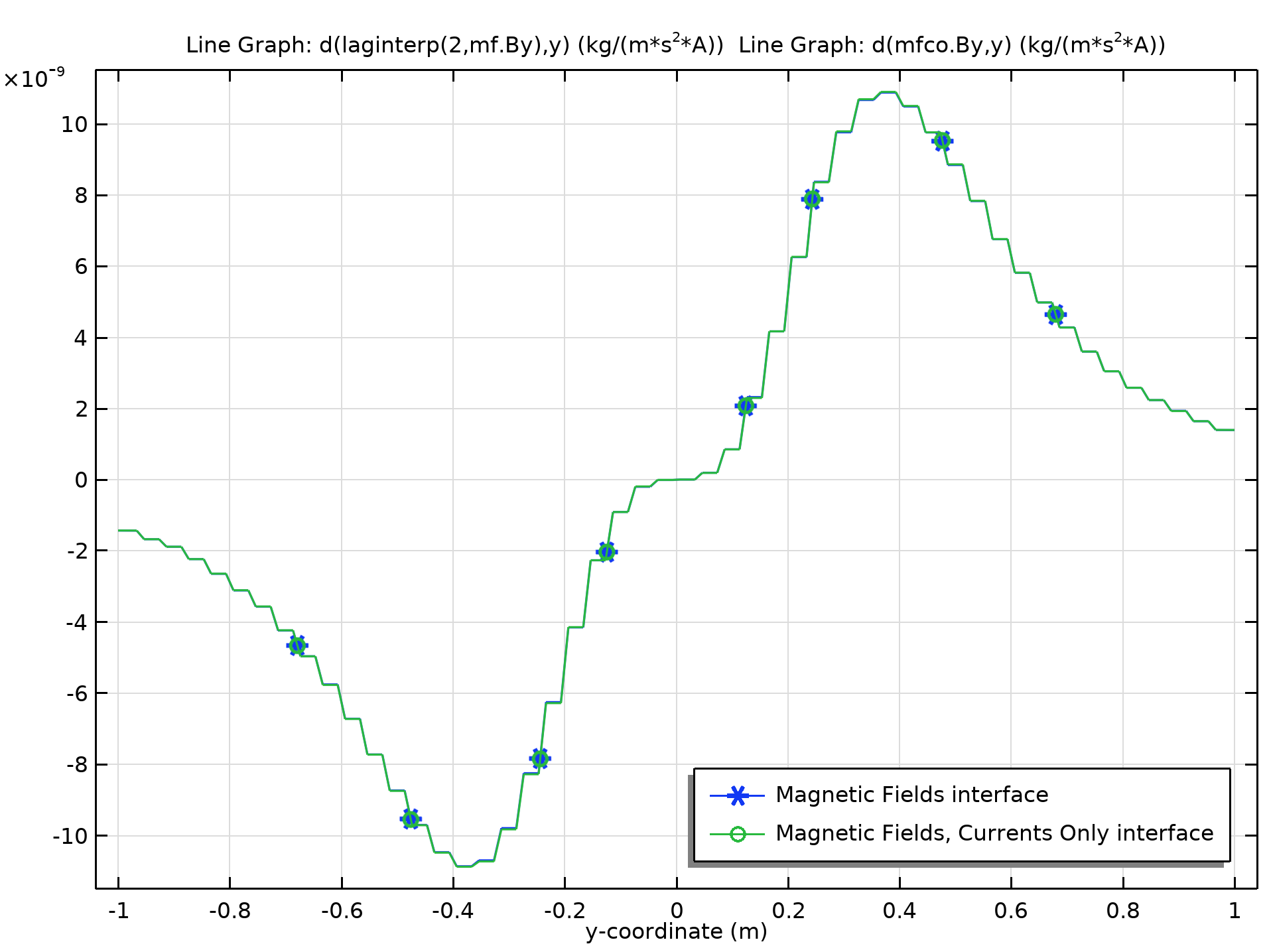
沿亥姆霍兹线圈中心线的磁通密度y 分量的梯度比较(相对于 y 方向)。
下一步
点击下方按钮,进入 COMSOL 案例下载页面,下载亥姆霍兹线圈的磁场模型。
如果您想了解更多关于 COMSOL Multiphysics 及其附加的 AC/DC 模块的特点和功能,请查看以下资源:



评论 (0)