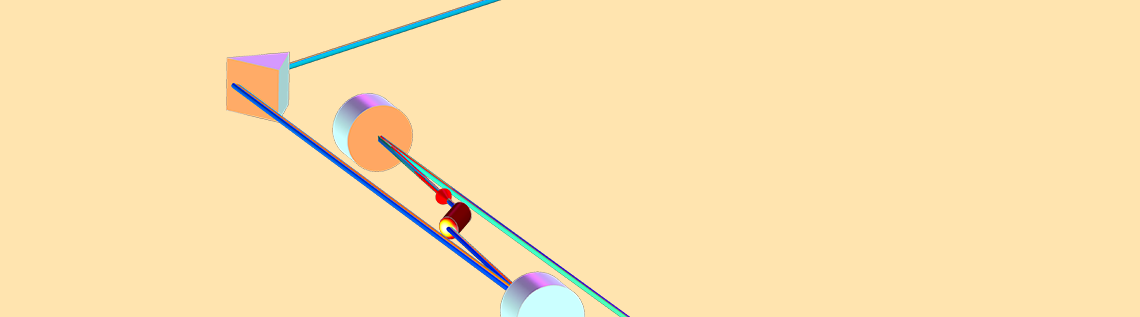
姿态探测指在三维空间中测量物体的方向和旋转,这种技术对于飞机与航天器的导航至关重要。最近的研究证实,环形激光陀螺仪和纤维环陀螺仪能够替代传统的机械陀螺仪,精确地测量旋转运动。此装置的基本工作原理是一种被称作萨格纳克效应的光学现象。在本文中,我们将利用射线光学仿真,观察简单萨格纳克干涉器中的萨格纳克效应。
究竟是我还是房间在旋转?
任何导航系统的一项基本任务是保持追踪物体的位置和方向,以及二者的变化率。导航系统对精度的要求达到了极致,特别是太空航行领域。举例来说,通信卫星可以敏感地响应千分之一度每小时的细微角速度。
系统对精度的要求固然令人生畏,不过事实上姿态控制的基本任务可以归纳为一个简单的问题:如何确定我的旋转速度以及旋转轴?
原则上讲,对于任意旋转坐标系中的任何观测者而言,这个任务都是相同的,即便是旋转餐厅中的宾客也不例外。

印度国宾大酒店的旋转餐厅的照片,它是印度历史最悠久的旋转餐厅。该照片由 AryaSnow 拍摄,已获CC BY-SA 4.0授权,并通过Wikimedia Commons共享。
假设你坐在旋转餐厅里面就餐,现在正在推断餐厅的角速度 Ω(单位:rad/s)。
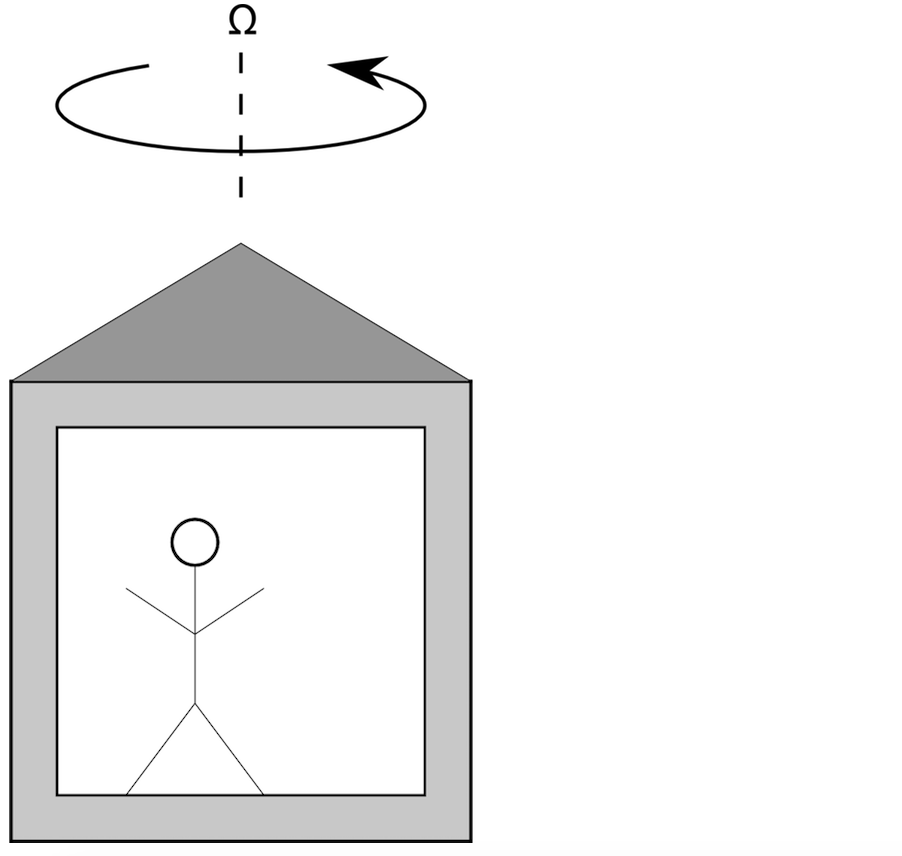
最简单的方法就是往外看。选取一个静止的目标,比如建筑物或树,然后观察在你的视野中它的位置是否会随时间变化。
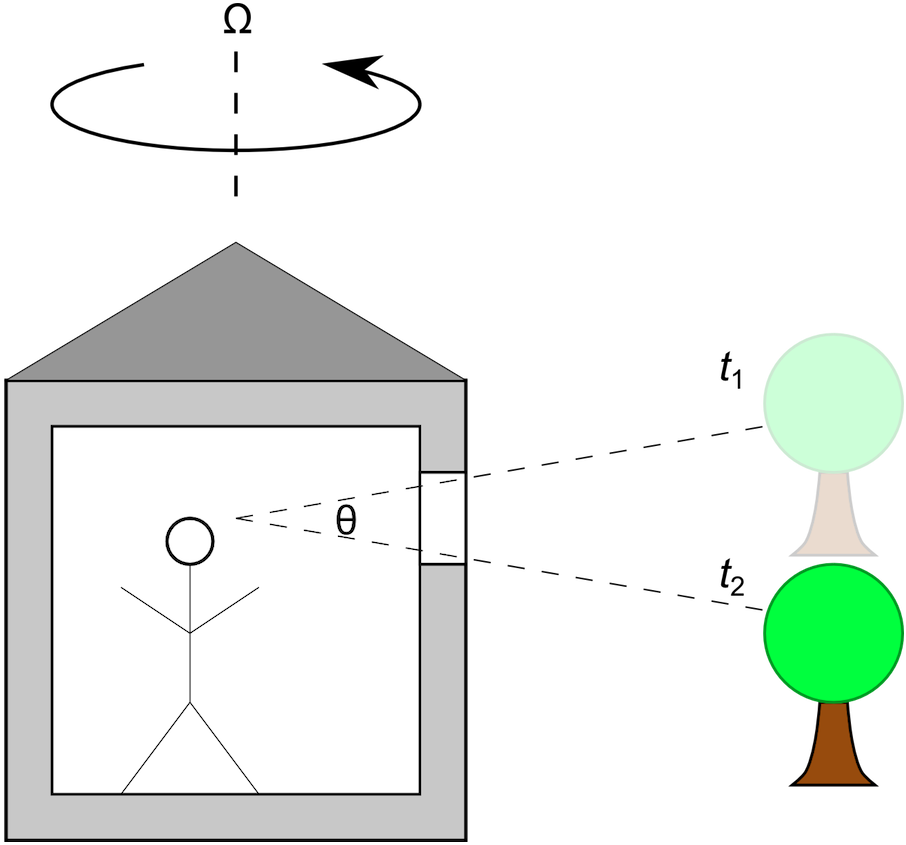
上图展示了在观察者的视野中(比如从窗户往外看),树在初始时间t1和时间t2时的位置。设两个视线之间的角度为 θ(单位:度)。如果相对于餐厅本身的大小,树的距离很远,角速度的计算公式则为
太空中的相似场景
太空航行的难度比在餐厅吃饭大得多,所以我们必须注意几个额外事项。在太空中,“静止物体”的方法比较难实现。举例来说,当我们利用太阳敏感器对地球静止轨道上的卫星进行姿态控制时,还要考虑地球绕太阳转动的相对运动。相比之下,恒星敏感器的精度极其可靠,这是因为基于各种目标前提,我们可以认为恒星在太空的位置是始终不变的,且恒星更接近于一个光点,而不是有一定角度的连续光源。
除此之外,在航天器姿态测量与控制对精度的严苛标准下,被观测物体的有限尺寸也需要考虑到,比如当你看向太阳时,要知道自己在观察太阳的哪一部分。在三维空间中实现任意旋转至少需要两个物体,否则你不能判断旋转轴的方向。
遮住视野
现在我们又回到原来的餐厅,只不过这次窗户都关上了。既然向外看的视线被遮挡住了,你不能依赖于任何物体来判断旋转坐标系。
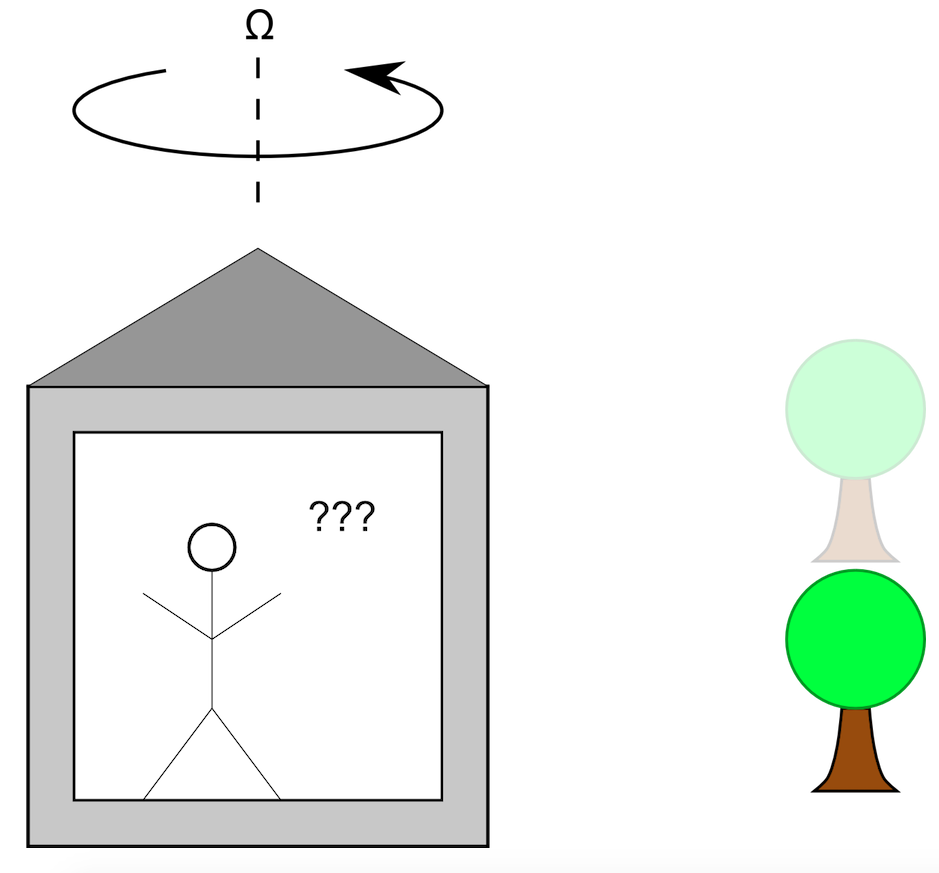
我们可以在旋转坐标系内做几个实验来确定它的角速度。比如在地板上放一个球,观察离心力是否会使它滚动(这时你需要知道旋转轴的位置——在太空航行中可不一定行!)。另一个方法是使用机械陀螺仪。
下个章节将解释第三种方法——利用光的特性;准确地说,真空中的光在所有坐标系中拥有相同速度的特性。光在旋转坐标系中传播时,它揭示了一种被称作萨格纳克效应的现象。环形激光陀螺仪就是利用了这种效应。这种陀螺仪广泛取代了利用高速回转体的传统机械式陀螺仪,环形激光陀螺仪舍弃了活动部件,因此维护成本更低。
解释萨格纳克效应
观察萨格纳克效应最简单的方法是:利用两束在同一个圆环中对向传播——即反向运动——的光线。圆环以恒定的角速度 Ω 逆时针旋转。(国际单位是弧度每秒,不过在惯性导航系统中,我们可以用度每秒来代替它。)
初始时,两束光线从圆环的 P0点发射,沿圆环以光速反向传播,与此同时,发射点开始绕坐标系旋转。当沿顺时针方向传播的光线与发射点再次重合时,重合点为一个新的位置 P1,传播距离略小于一个完整的圆。当沿逆时针方向传播的光线与发射点重合时,重合点为另一个不同的位置 P2,其传播距离大于一个完整的圆。
当然,这里的运动显然被夸大了。在现实中,P0同 P1和 P2(以及后者之间)的位移可能小一百亿倍!但是因为两束光线的距离差伴随着相移,而相移会在两束光线之间产生干涉图案,所以两束光线的传播距离的细微差别(同理还有传播时间)还是可检测到的。若设 ΔL为两束光线传播的距离差,则
(1)
其中,A是圆环面积,真空光速为c0= 299,792,458 m/s。
事实证明,方程(1)不仅符合环形路径,也适用于其他形状。光程差只取决于环路的封闭面积,而不是形状。我们可以根据广义相对论推导出方程(1)的一般表达式。方程的核心在于,萨格纳克效应是一种相对论现象,对于这种现象,经典推导可以得到相同的一阶结果。参考文献1–2。
利用射线光学仿真演示萨格纳克效应
在本节中,我们将研究简单的萨格纳克干涉仪模型。它的基本工作原理与环形激光陀螺仪相同,不过前者不需要考虑光束路径上的激光介质,所以模型创建步骤更加简单。(除了强度更大之外,激光介质还会引入很多其他复杂性,比如色散效应,不过为了方便描述,我们可以忽略。)但是,对于给定的萨格纳克干涉仪模型几何与拥有相同镜子布局的环形激光干涉仪,二者会产生同样的光程差和相位延迟,所以这个模型依旧可以提供大量信息。
基本的萨格纳克干涉仪几何由一个分光器、两面镜子和一个可吸收射出光线的障碍物组成。图示如下。
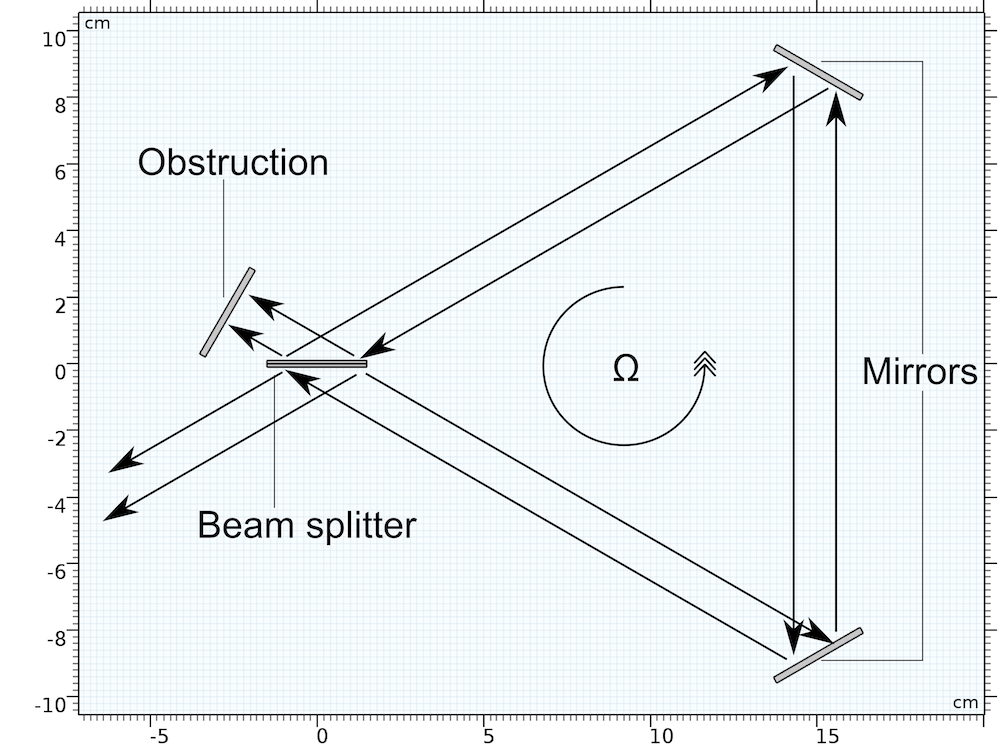
此模型的几何参数见下表。
| 参数名称 | 公式 | 值 | 描述 |
|---|---|---|---|
| λ0 | N/A | 632.8 nm | 真空波长 |
| R | N/A | 10 cm | 圆环半径 |
| b | b=R\sqrt{3} | 17.3 cm | 三角形边长 |
| P | P = 3b | 52.0 cm | 三角形周长 |
| A | A = b^2 \sqrt{3}/4 | 130 cm2 | 三角形面积 |
几何结构有时被设计成正方形,而不是三角形,这时三个镜子位于三个顶点上,分光器在另一个顶点上。系统中光线的传播路径通过方向箭头来表示。由于整个装置沿逆时针方向旋转,因此在碰到障碍物之前,沿逆时针方向发射的光线比顺时针光线的传播距离稍远一些。
为了直观演示这一现象,请观看下方动画(请注意,旋转运动又被夸大了一百亿倍!)。
在左侧动画中,观察者站在惯性(非加速)坐标系中。虽然光线的传播路径都是直线,但是它们撞击镜子的时间却不一样。在右侧动画中,观察者“乘坐”着宇宙飞船,可视为身处非惯性坐标系中(严格来说,即使在旋转坐标系中,对向传播的光线的运动速度也相同;任何坐标系中光速均不变!)。
代入上文给出的几何结构参数,方程(1)计算出两束对向传播光线之间的光程差为 8 × 10-16米,即 0.8 飞米,约等于质子的半径;这个数值显然很难测量!萨格纳克干涉仪和环形激光陀螺仪通常不会直接给出光程长,而是报告频率差或者拍频Δν,其公式为:
(2)
其中 ν(Hz)是光的频率,L是沿三角形周长传播的光的光程长度。
注意,L不一定是三角形的周长,因为系统中可能存在共用运动的介质,比如沿光束路径、折射率不等于 1(n ≠ 1)的激光介质。在本例中,假设镜子和分光器之间为真空空间。则拍频的数量级为 1 Hz,当然比质子半径的距离容易测量得多。
该模型利用几何光学 接口来追踪萨格纳克干涉仪几何中的光线。两个镜子被施加了专门产生镜面反射的镜像 边界条件。分光器采用了材料不连续性 边界条件,用户定义的反射比为 0.5,所以两个对向传播光束具有相同的强度。
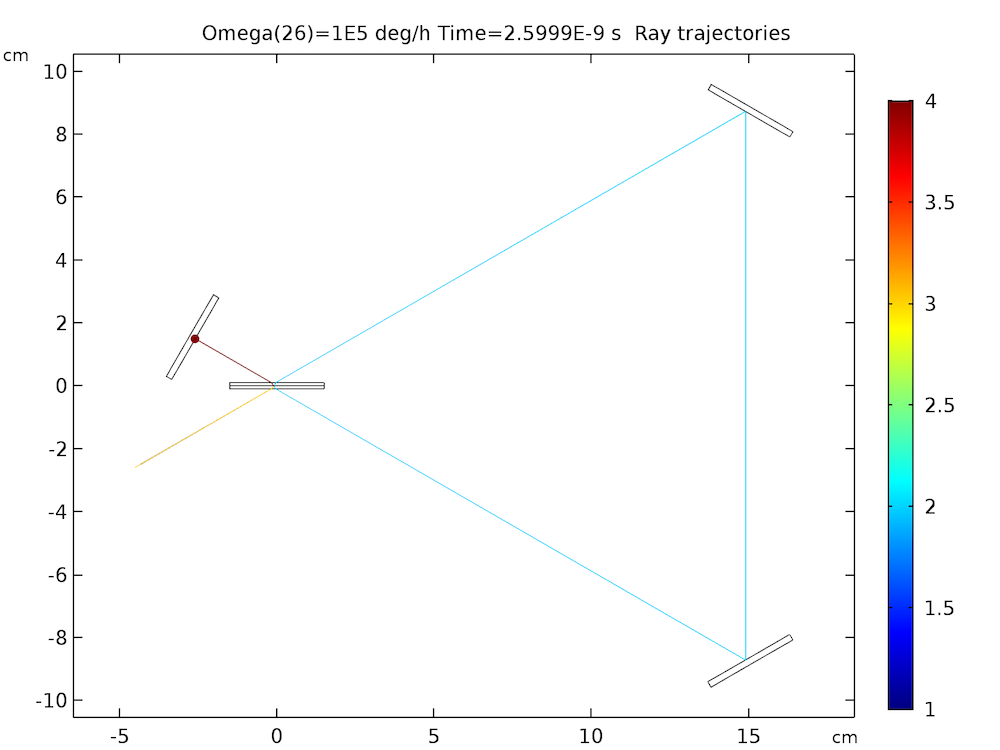
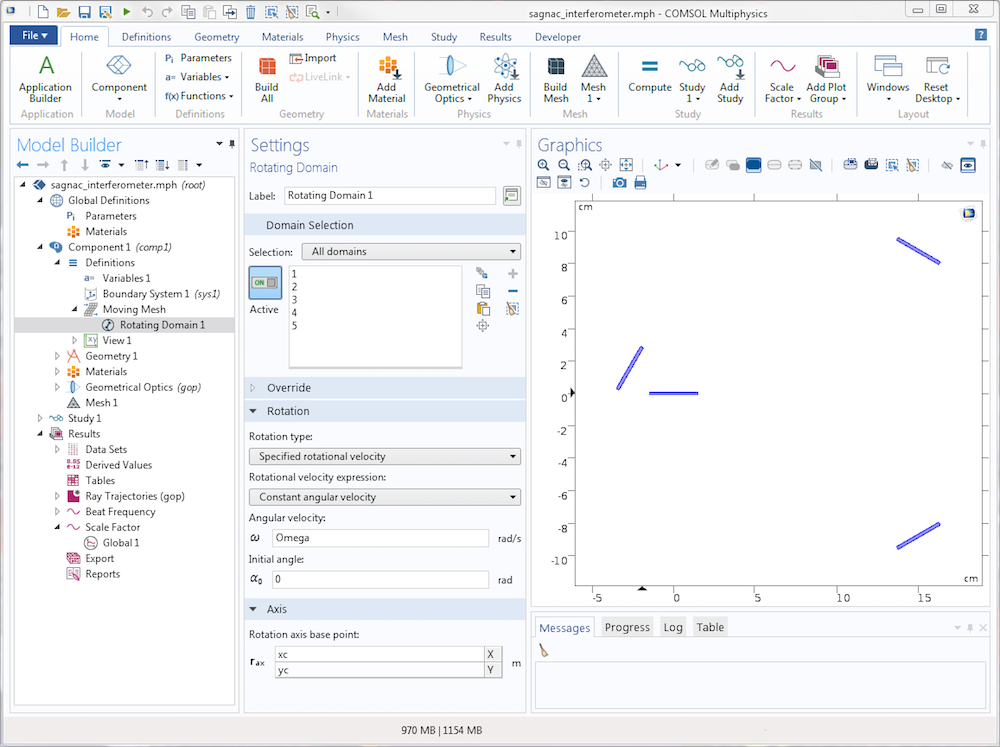
我们还利用了旋转域 特征使装置旋转,如下图所示:
所得绘图显示了镜面光学系统中沿两个方向传播的光线,然而由于与光速相比,镜子的移动速度非常慢,所以我们很难将两个路径区分开。如果放大一百亿左右,才能辨别出两个隔着微小距离的三角形。
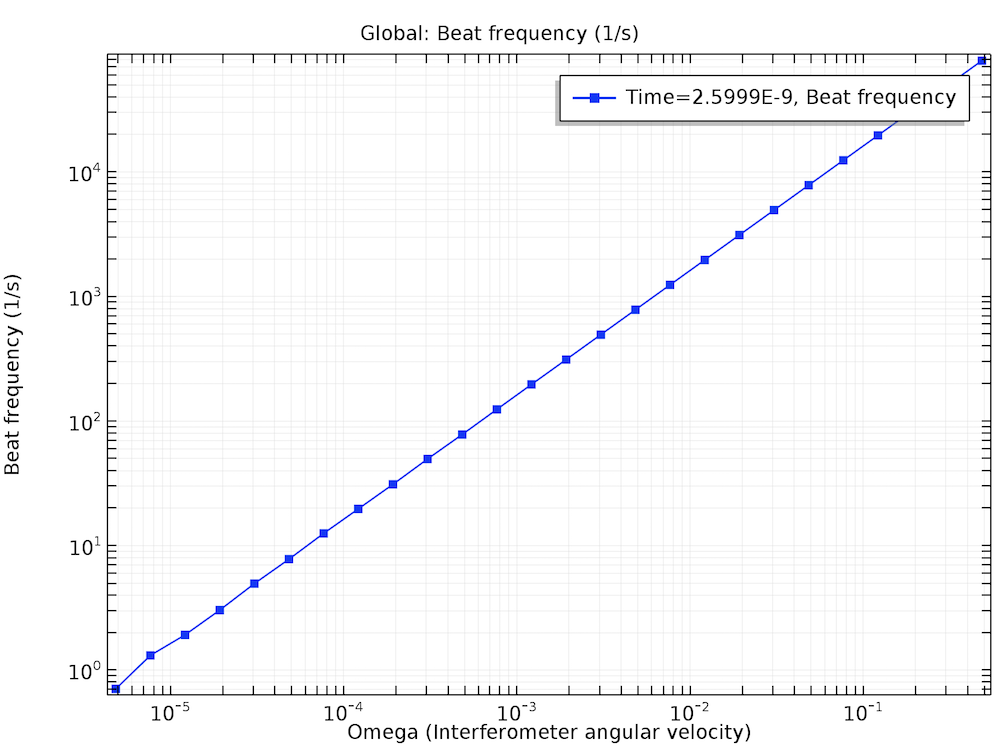
在下方绘图中,拍频是干涉仪角速度的函数。二者函数关系是线性的,符合方程(1)–(2)。绘图左下角出现了一些数值噪声。这是数值精度造成的,在模型文档中将解释更多细节。
姿态探测应用于航空航天导航
上文提到的萨格纳克干涉仪和相关装置——包括环形激光陀螺仪和光纤陀螺仪——都属于惯性导航系统的现实应用;惯性导航系统以一个已知位置为起点,将平移速度和角速度随时间的变化整合在一起,从而预测物体的位置和方向。现实中,惯性导航系统通常需要与以太空中其他物体为参照物的绝对位置和绝对方向测量相结合。绝对测量可以利用地球敏感器、太阳敏感器或恒星敏感器;利用地球表面已知位置上的射频信标;利用地球磁场测量;或者利用以上任意组合来完成。
平移速度和角速度的微小测量误差会导致惯性导航系统随时间推移变得越来越不稳定。使用以上任意一种敏感器定期进行绝对测量,有利于将不确定性限制在一个更合理的数值内。下图预测了不确定性随时间的变化。
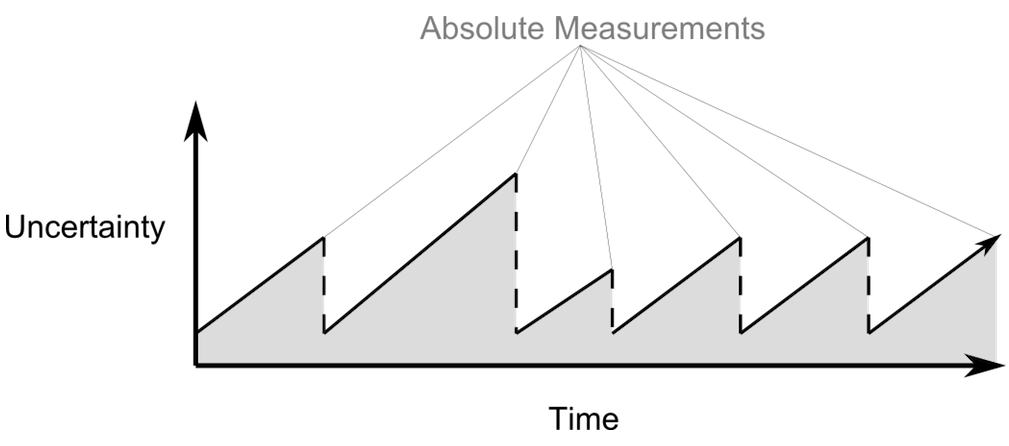
结论
我们成功地利用射线光学仿真演示了简单干涉仪内的萨格纳克效应。只要所有活动部件的速度远远小于光速,拍频便符合基于广义相对论的严密理论。萨格纳克干涉仪或环形激光陀螺仪之内的光程差的大小仅仅取决于对向传播光束所围住的面积,而非圆环的几何结构。
下一步操作
点击下方按钮,探索萨格纳克干涉仪模型。在“案例下载”页面中登录 COMSOL 账号登录,即可下载 MPH 文件(需要有效的软件许可证)及模型教程。
参考文献
- Post, Evert J. “Sagnac effect”,Reviews of Modern Physics, 39, no. 2, p. 475, 1967.
- Chow, W.W. et al. “The ring laser gyro”,Reviews of Modern Physics, 57, no. 1, p. 61, 1985.



评论 (0)