
使用形状优化可以增强许多应用领域的器件设计,包括电磁和射频(RF)应用。在这篇博客中,我们将通过两个案例,来说明使用形状优化所能获得的好处,并展示将 COMSOL Multiphysics®软件中的形状优化功能应用于微波和毫米波时可以实现的目标。
本文是关于电磁仿真形状优化系列博客的第二篇博客。第一篇博客侧重于波动光学中的形状优化。点击此处,阅读第 1 部分内容。
背景信息
在深入研究形状优化之前,我们需要了解为什么可能会使用它而不是参数优化。形状优化和参数优化之间的主要区别在于,形状优化通过对网格进行变形来实现,这使得网格与基于梯度的优化兼容。这样可以提高方法的效率,并可以在标准工作站上以合理的计算时间优化数千个控制变量。虽然参数优化有它自身的好处,但由于它与基于梯度的优化不兼容,所以计算速度也很慢。正如这个系列的第一篇文章”电磁仿真中的形状优化:第 1 部分”中所解释的那样,这“限制了优化变量的数量,从而限制了设计自由度”。这就是我们在本系列中介绍形状优化的主要原因。
本文介绍的案例将使用移动渐近线(MMA)的方法作为优化算法来求解。特别地,我们将使用这个方法的全局收敛法,GCMMA,因为它通常能为最小最大值问题提供精确的结果。该方法还支持移动限制,从而降低了出现反转单元的可能性。基于这两个原因,形状优化是大多数形状优化问题的首选优化方法。但是请注意,也可以使用二阶方法(如 IPOPT 或 SNOPT)进行优化,对于简单的问题,其收敛可能比移动渐近线更快。
案例 1:滤波器
首先,我们以波导虹膜带通滤波器的优化 — 变换版本模型为例考虑形状优化。使用参数优化解决这个问题相对简单,但是形状优化更快。这个模型在概念上与第一部分博客中的滤波器案例相似,并且这两个案例都使用了变换功能。但是,本示例中的几何形状不同,并且使用了最小最大值目标:
其中f_\mathrm{pass}是通过频率,\mathrm{S11}_\mathrm{dB}和\mathrm{S21}_\mathrm{dB}是 S 参数的对数值。
该几何结构由四个虹膜组成,通过使用变换功能控制其中两个虹膜的大小来优化这些虹膜。在相邻的边界上使用对称/辊支承功能,以便更改虹膜的位置。请注意,两个虹膜可以彼此独立地变化,因为如果选择由不共享点的不同组组成,变换功能就会自动拆分选择。当有许多对象需要优化时,这一点特别方便,就像本系列博客文章的第一部分所演示的那样。在这个示例中,通过使用广义拉伸算子复制变形来保持双重对称性。生成的几何设计和 S 参数绘制在下图中。
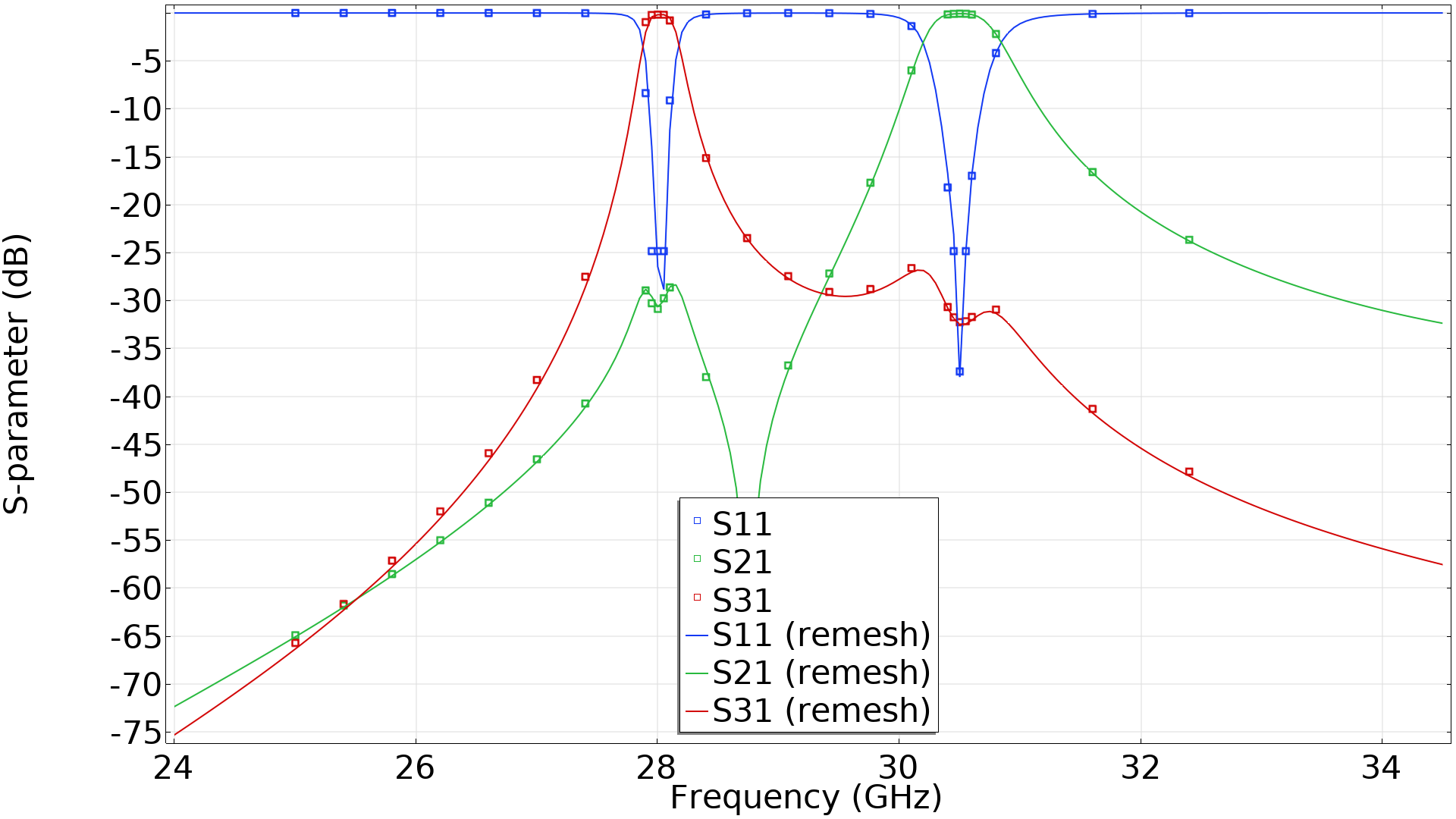
用黑线绘制的设计是形状优化后的 RF 滤波器(左)。灰色椭圆中的线条被优化,并将形状变化复制到其他线条,以保持双重对称性。相应的 S 参数作为频率的函数被绘制在右侧图形中。图中的点表示用于优化的频率。
优化的设计可以被拉伸,以便在三维组件中被验证性能,如上图中的线条所示。
就像波导虹膜带通滤波器的优化 — 多项式版本案例中所演示的那样, 还可以通过将多项式边界功能与不同的初始几何形状结合来设计滤波器。这增加了 33% 的控制变量和稍好的目标(用于三维验证),但它也有更加尖锐的角。我们很难事先预测特定应用的最佳策略,并且通常会以更大的设计自由度实现更高的性能,但这在设计过程的后期可能会付出高昂的代价。因此,必须经常在高性能和成本之间做出妥协。COMSOL®能够以不同的方式轻松设置同一问题,并具有不同的设计自由度,从而为用户提供了做出明智决策所需的数据。
示例 2:双工器
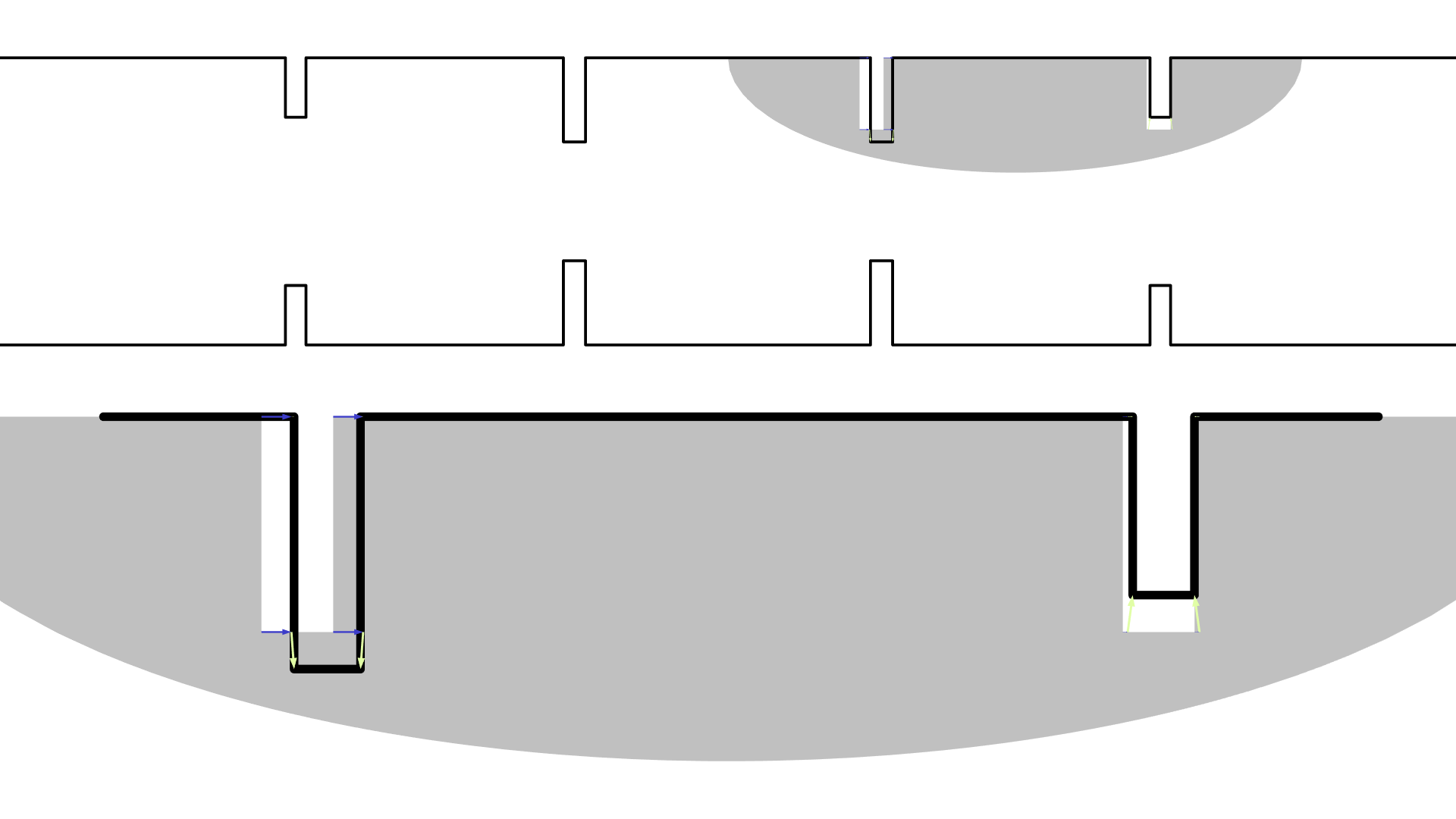
第二个案例是双工器,这个想法是接受一个输入信号并将它路由到不同频率的不同输出端口。这类似于第一篇博客中的第二个示例,只是这里我们将使用多项式边界功能。几何图形中顶点的坐标已经被优化了,但由于使用了一阶多项式,因此线条仍保持直线。此外,虽然目标函数的规范遵循与前面概述的相同思路,但希望输出频谱在带外抑制范围内没有峰值(共振)。强制执行这一点需要某种复杂的表达。目标函数的表述可以在使用形状优化为 5G 移动网络设计波导双工器案例中看到。在与输入和输出端口相邻的线路上应用对称/辊支承功能,使这些线可以更改长度,但不能更改方向。下面的动画演示了优化过程。
动画显示了优化期间两个通频的电场的 z 分量。它还显示了相关的 S 参数。
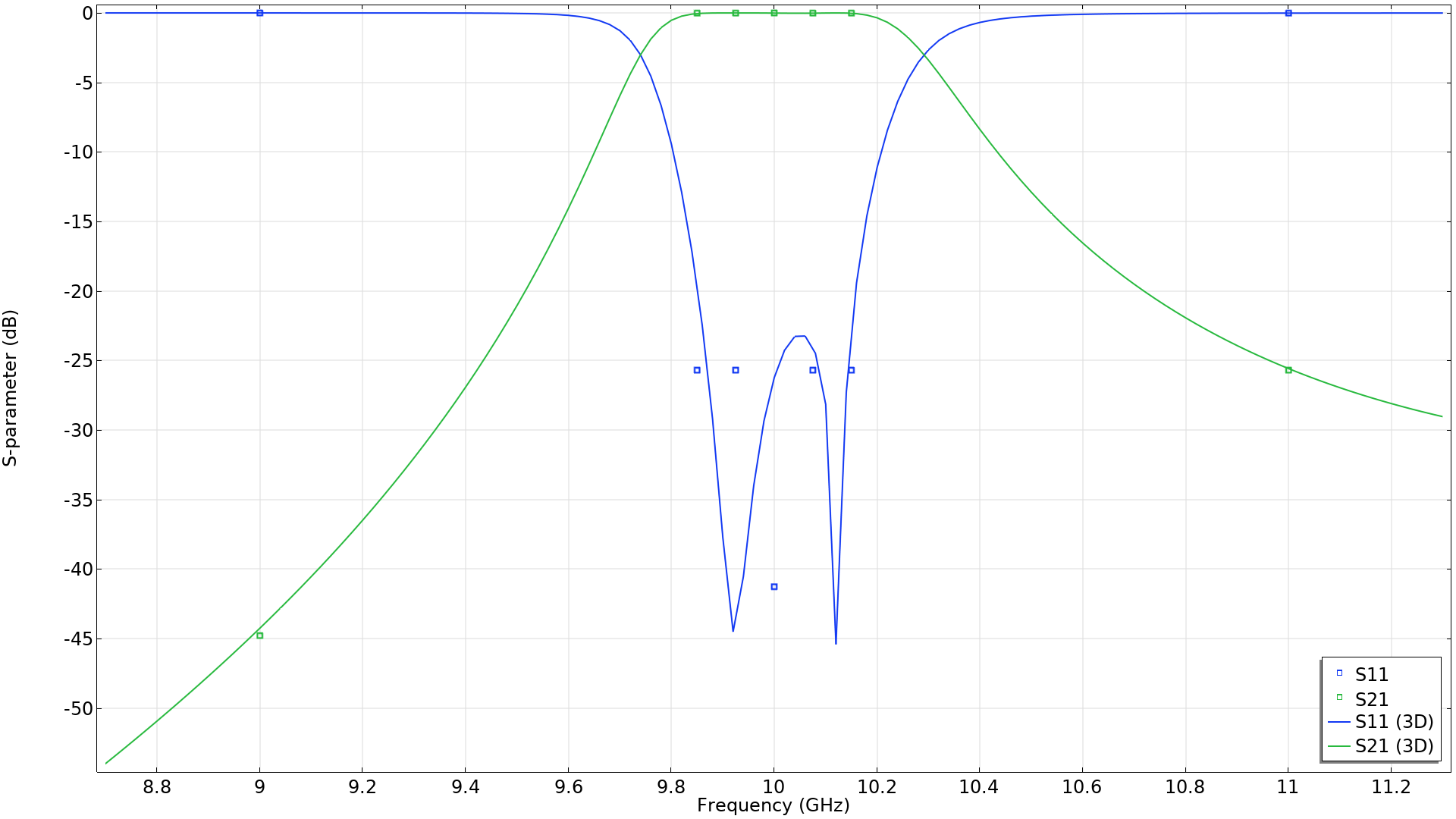
用于优化的频率在下图中被绘制为点,而线条表示基于变形构型中生成的网格具有更精细分辨率的频率扫描。
如上图中的点所示,该问题需要计算 26 个频率,但每个频率使用两个目标函数——因此计算灵敏度需要解决 52 个线性问题。这是一个令人尴尬的并行问题,下图演示了如何使用集群功能减少计算时间。
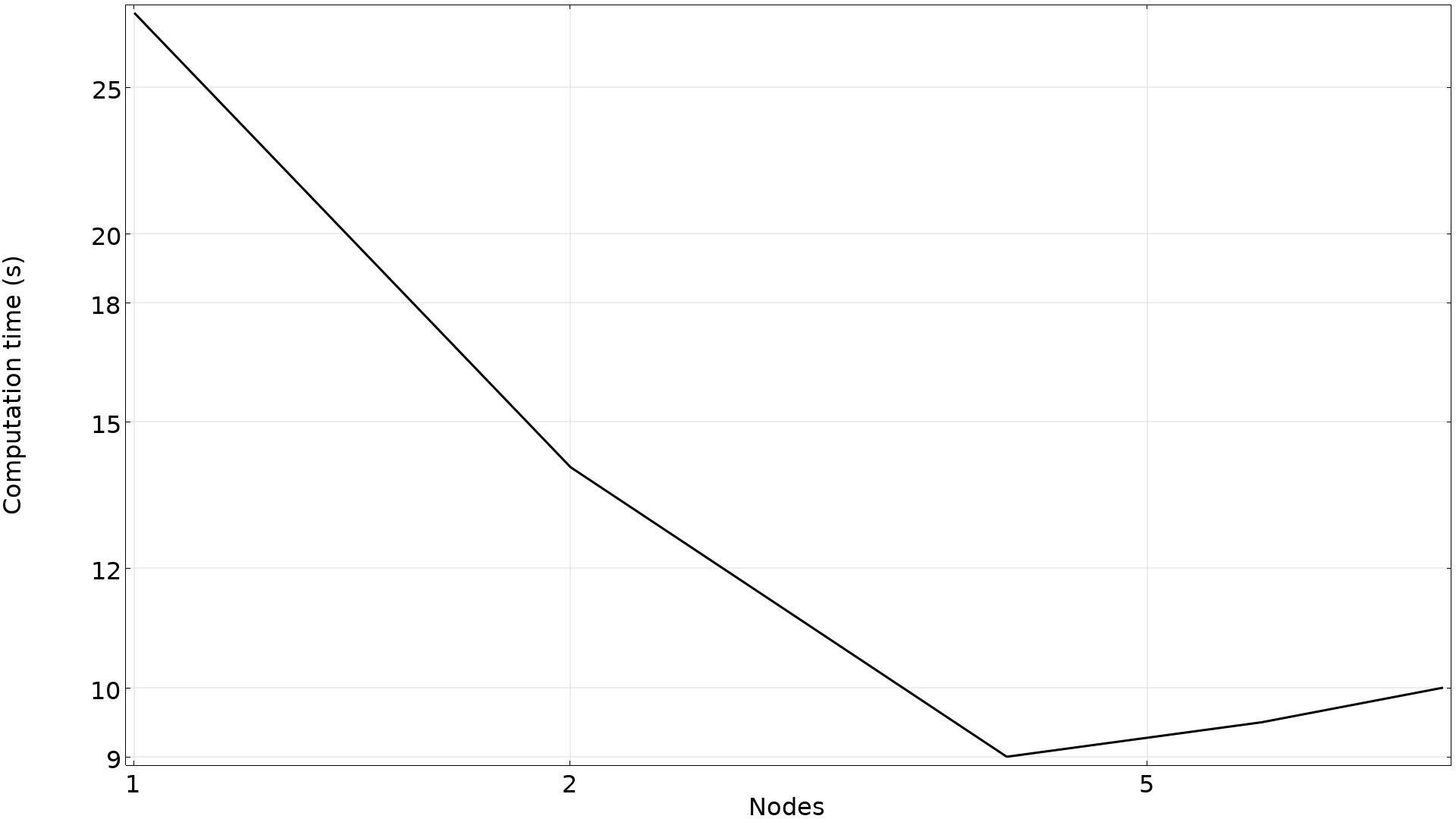
对集群上的 1、2、4 和 8 个节点的单个优化迭代的计算时间进行了说明。即使模型只有 8.5 k 的自由度,在 4 个节点上也可以观察到良好的扩展性。但是,除了这一点,增加的通信成本超过了节省的计算时间,因此总计算时间实际上会增加。
良好的扩展性意味着使用 6 个节点可以在 30 分钟内解决优化问题。
结束语
在这个系列博客中,我们讨论了执行形状优化的好处,并介绍了电磁仿真中的几个示例。请注意,虽然本系列侧重于二维形状优化,但也可以对三维波传播问题进行形状优化。
后续步骤
有兴趣使用其他关于形状优化的教学模型吗?建议阅读下列案例:
- 要了解如何使用多项式边界功能设计具有三角形虹膜的滤波器,请下载波导虹膜带通滤波器的优化 — 多项式版本模型。
- 如果您有兴趣使用广义拉伸算子在模型中保持一定的壁厚和/或在满足特定条件后停止优化,请查看热水器的形状优化案例模型。
- 要查看对三维波传播问题进行形状优化的示例,请下载模型中矩形扬声器喇叭的形状优化—三维。



评论 (0)