到底要不要倒圆角?这个问题可能会对多物理场仿真分析人员造成困扰。在构建有限元模型时,锋利的边会导致局部奇点和细化网格的场不收敛。通过添加一个圆角使这些锋利的边变圆可以避免产生这样的奇点。然而,事实证明在许多多物理场模型中,这些尖锋利的边和由此产生的奇点不一定会对结果产生负面影响。接下来,我们来了解更多详细内容。
尖角周围的电磁加热
使用COMSOL Multiphysics® 软件求解的一个最常见问题是电磁加热问题,它结合了麦克斯韦方程组(求解电流和总损耗)的解和传热方程(求解温度曲线)的解。
如上一篇博客所述,在求解电磁场时,尖锐的凹角会导致局部不收敛的电场和电流密度。电磁损耗是电场和电流密度的乘积,因此尖角处的峰值损耗会随着网格细化而趋于无穷大。
然而,随着网格细化,尖角周围损耗的积分将收敛。这是有限元方法的优点之一,它以所谓的“弱形式”求解控制方程,满足积分意义上的控制偏微分方程:最小化模型中的总误差,但允许(可能是无穷!)局部错误。
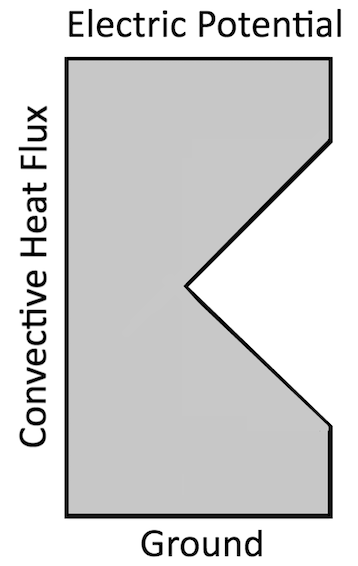
一个简单的电磁加热问题的示意图,在内部尖角处有一个奇点。
如上图所示,我们用一个简单的例子来复习一下奇点的概念。施加在一个有尖锐缺口的矩形域上的电位差导致材料产生电流和电阻损耗。
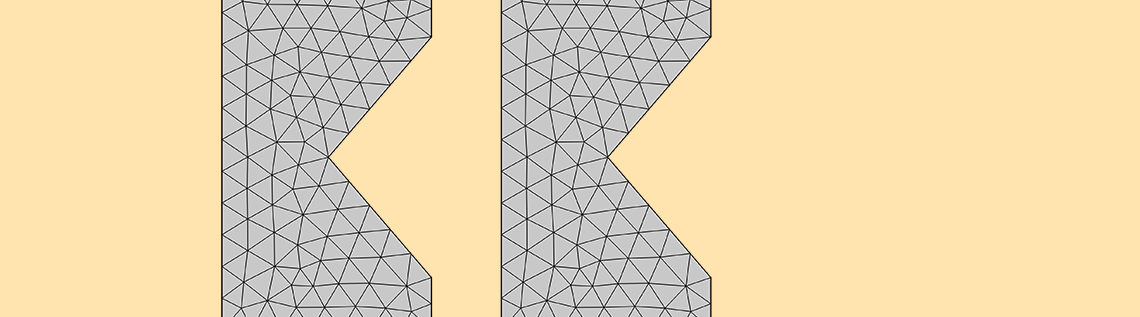
下图中,我们看到了电阻损耗的彩色绘图,以及在内尖角处使用的不同级别的细化网格。在最高级别的细化网格下,损耗似乎在尖角附近非常集中。
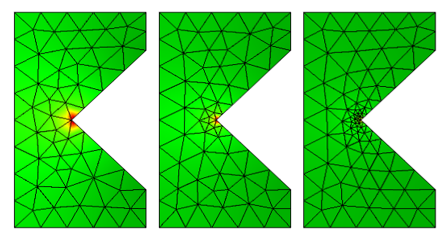
使用不同级别的细化网格求解的电磁损耗。
在这个内尖角处,理论上电场是无限大的,因为这种几何形状和边界条件意味着电流必须在某一点瞬间改变方向。另外请注意,外尖角不会导致奇点。由于这种几何形状和边界条件,电流不会立即在这些点上改变方向。
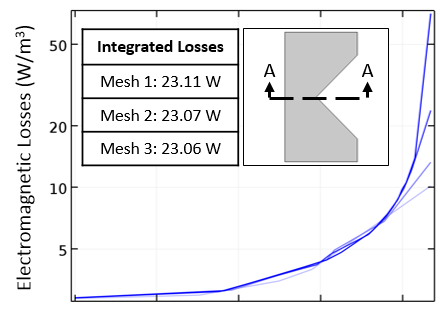
沿切线绘制的用对数标尺表示的电阻损耗图,不同级别的细化网格对应的损耗积分表格。
如果我们在横截面上绘制损耗,如上图所示,可以观察到随着网格的细化,尖点处的损耗越来越大。然而,域上的损耗积分(简单来说,就是曲线下方的区域)会随着网格细化很快收敛。
现在,通过额外求解稳态条件下的温度分布传热方程,我们将这个问题变成一个多物理场问题。下图绘制了使用不同级别的细化网格求解的温度场,以及尖点处的温度。
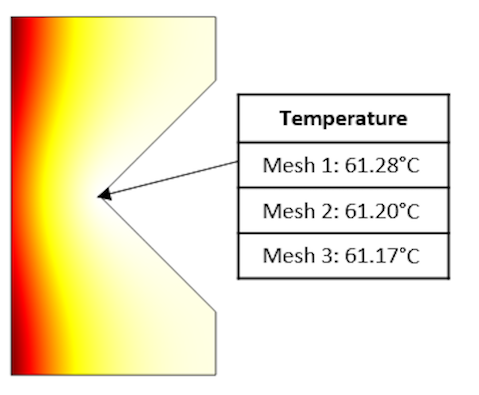
使用不同级别的细化网格计算的尖角处的温度场和温度值表格。
从上述结果可以看到,奇点处的温度,当然还有其他地方,对网格细化程度也非常不敏感。这有两个原因。首先,正如我们看到的,总电阻损耗对网格非常不敏感。其次,只要总热载荷相似,稳态传热控制方程的扩散将回到非常接近的温度解。另一方面,如果热载荷非常高,瞬态温度解可以预测非常高的局部温度,但尽管很及时,这也是一个局部的和相对的影响。也就是说,空间热载荷分布的尖峰将随着时间的推移而变得平滑,并且在非常长的仿真时间的限制下,瞬态解将接近稳态解。
结束语
从这些信息中我们可以得出什么结论呢?如果你正在求解一个电磁加热问题,并且只对计算总电磁损耗和温度分布感兴趣,那么通常可以不用在模型中添加圆角。
这样做的优势是双重的。你不需要进行向几何体添加任何圆角的 CAD 建模工作,也不需要在尖角处过度细化网格,这可以为你节省最宝贵的资源:时间!



评论 (0)