
加热的肥皂泡、波浪状的云和木星大红斑有什么共同之处?它们的形成取决于以不同速度运动的两股平行气流之间的剪切层的动力学。这种不稳定运动被称为开尔文-亥姆霍兹不稳定性(Kelvin-Helmholtz instability),它无处不在,比如在气候动力学等方面发挥着重要作用。这篇博客,让我们在计算流体动力学(CFD)分析的帮助下,深入研究这种不稳定性的发生和演变过程。
加热的肥皂泡
最近,我阅读了NewScientist上的一篇文章“Soap-bubble cyclone is a deadly storm in miniature”,文中报道了法国波尔多大学的一个物理学家团队从底部加热肥皂泡,创造出类似风暴的快速旋转的结构,产生的图案类似于地球大气中的热带气旋。这让我开始思考如何使用 COMSOL Multiphysics 对其进行建模。
首先,让我们来复习一下剪切层的概念。
什么是剪切层?
剪切层是一个有限厚度的区域,具有将不同速度运动的两股平行流分隔开的陡速度梯度。对于开尔文-亥姆霍兹不稳定性,剪切层的微小扰动会引发其演化为大尺度涡旋阵列,并消散为更小的涡旋。
可视化图像比文字更容易说明,让我们来看两种自然现象。
波状云
在下面的图中,你可以看到绵延起伏的波浪状云层,也称为巨浪。云层上方的气流向右移动,而云层可以是静止或者可以向左移动。云的分离平面(即切变层)上的微小扰动会引发滚动运动,从而使这些云呈现出特有的形状,提示此处有一个飞机应避开的高湍流区域。

由开尔文-亥姆霍兹不稳定性引起的滚动波状云。图片来源:GRAHAMUK。
木星大红斑
下图显示的木星大红斑形成于 150~300 年前,其大小约为地球的 2~3 倍,是太阳系中开尔文-亥姆霍兹不稳定性的最强烈表现。从这张图片中可以看到至少有 4 个剪切层,其中大红斑是被困在两个喷射流之间的最大涌流。

旅行者 2 号飞越木星拍摄的照片,显示大红斑附近的木星风暴。图片来源:NASA。
射流动力学建模
开尔文-亥姆霍兹不稳定性在自然界中随处可见,也可应用在工业领域,例如增强混合应用。通过仿真预测或防止开尔文-亥姆霍兹不稳定性的发生,对设计人员有很大帮助。
为了触发开尔文-亥姆霍兹不稳定性,需要定义一个初始速度场,该速度场由一个有限厚的、水平排列的剪切层和垂直速度扰动组成。使用COMSOL Multiphysics模拟射流时,我们可以使用文章“A Second-Order Projection Method for the Incompressible Navier Stokes Equations”中的数值。
我们希望使用以下表达式来表示初速度场:
u_{0} = \{ \begin{array}{l l} \tanh(30(y-0.25)) & \text{if} \quad y \leq 0.5 \\ \tanh(30(0.75-y)) & \text{if} \quad y > 0.5 \end{array}
v_{0}= 0.05 \sin(2 \pi x)
如果我们在 COMSOL 软件的初始值设置窗口中键入这些表达式:
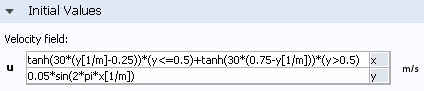
可以将速度场可视化:
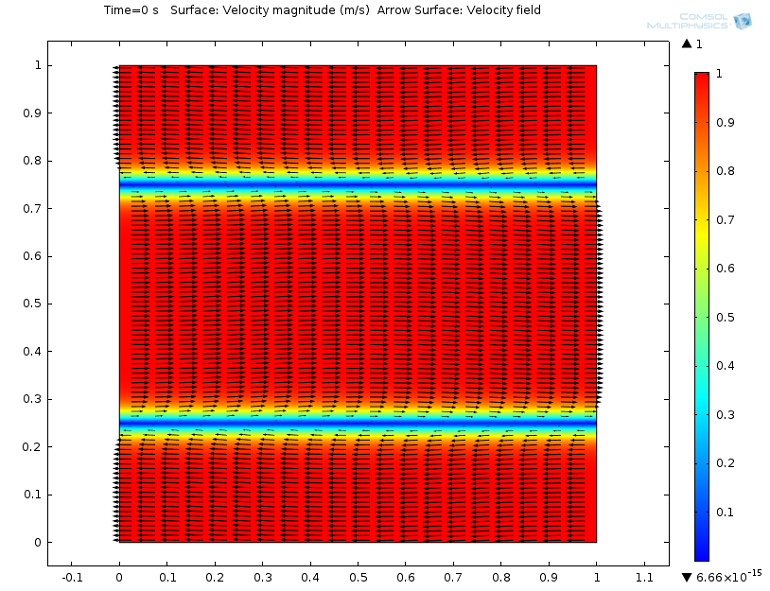
t=0s 时的速度大小和箭头表面图。
除了 CFD 分析之外,我们还可以通过质量传递模拟尝试模仿NewScientist文章中提到的肥皂泡气旋的结果。
我们希望使用以下初始浓度表达式:
c_{0} = \{ \begin{array}{l l} (1 + \tanh(30(y-0.25)))/2 & \text{if} \quad y \leq 0.5 \\ (1 + \tanh(30(0.75-y)))/2 & \text{if} \quad y > 0.5 \end{array}
如果在“初始值”设置窗口中键入该值:

我们可以将浓度可视化:
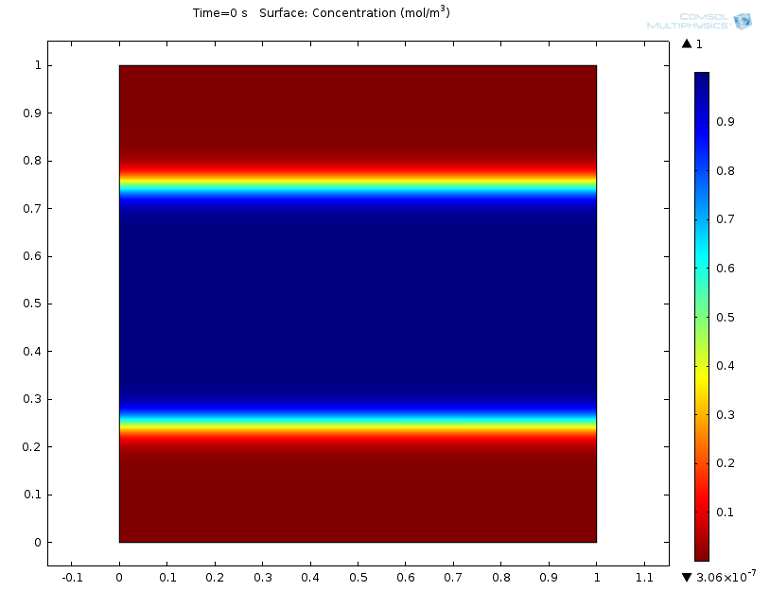
t=0s 时的浓度。
模拟在具有周期流动条件的单位方格内进行,以使初始速度场发展成一个双周期剪切层。为生成上述结果,密度和黏度应该分别设置为 1 kg/m3和 10-4Pa-s。质量传递模拟也应使用类似的周期条件。
通过仿真仔细观察剪切层
仿真结果显示了中心射流周围的剪切层是如何演变成周期性涡旋的,如下图所示。可以观察到三个涡旋,其中两个在上面,逆时针旋转,一个在下面,顺时针旋转。剪切层包裹着这些涡旋,并在开尔文-亥尔姆霍兹不稳定性引起的大应变场作用下逐渐变薄。动能从射流转移到剪切层,剪切层将继续变薄并消散成更小的涡旋。
CFD 分析结果动画。左上图:压力场。右上图:速度大小和箭头面。左下图:涡度表面、涡度等值线和速度箭头表面。右下图:箭头线。左图例:涡度 [1/a]。右上图例:压力 [Pa]。右下图例:速度幅值 [m/s]。
考虑到初始值的对称性以及我们使用的边界条件,顶层和底层的演化是镜像的。下图是 t=2s 时的结果。由于网格不够精细,无法解析流动细节,涡度场的高频分量模糊不清。
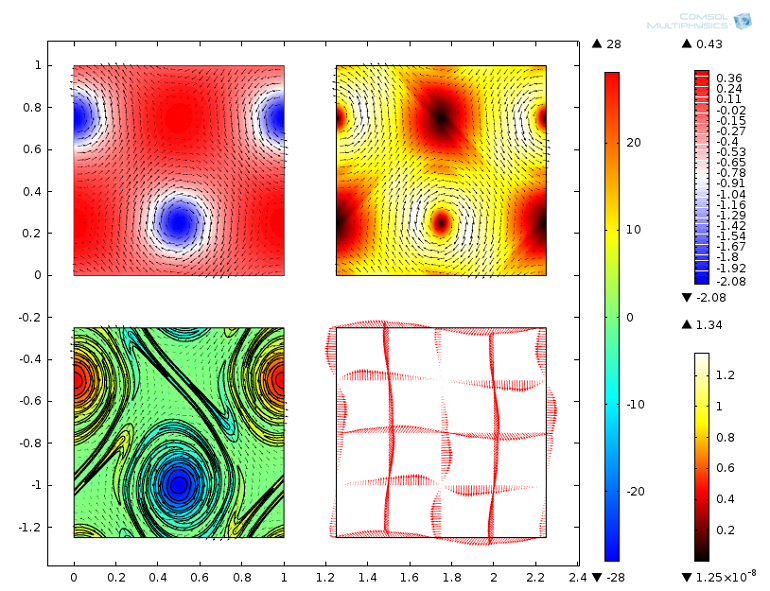
t=2s 时的 CFD 分析结果。
为了克服这些限制,需要更精细的网格,但这会导致更高的内存需求和更长的计算时间(这两者都不在本博客的讨论范围之内)。尽管如此,在本次模拟中,较大的旋涡并没有表现出振荡或形状扭曲,这表明射流的整体动态行为得到了很好的解析。它们的起始速度通常很慢,直到达到一个不稳定性迅速充分发展的点。
在质量传递模拟中,我们假设浓度扩散并被动地由射流吸附。在下面的模拟结果中,可以注意到,即使在扩散机理存在的情况下,浓度的动态变化也紧跟着射流的变化。模拟结果类似于NewScientist肥皂泡文章中讨论的现象。
质量传递模拟动画。图例:浓度 [mol/m3]。
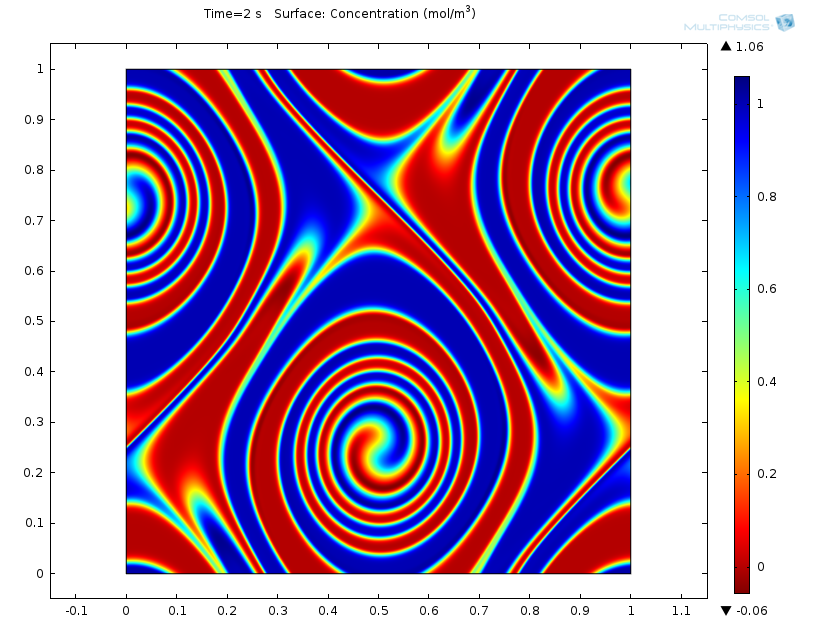
t=2s 时的质量传递模拟结果。
在利用仿真研究物理现象的动力学时,后处理非常重要,因为它可以佐证物理直觉,让我们更好地了解我们正在研究的东西,或者显示出意想不到的行为。对于这个示例,我们可以预期灰尘或冰晶会被困在涡旋中。
在这里,我使用 COMSOL 的粒子追踪模块来模拟这种情况。动画和粒子轨迹图证实了我们的直观预期。
粒子追踪模拟动画。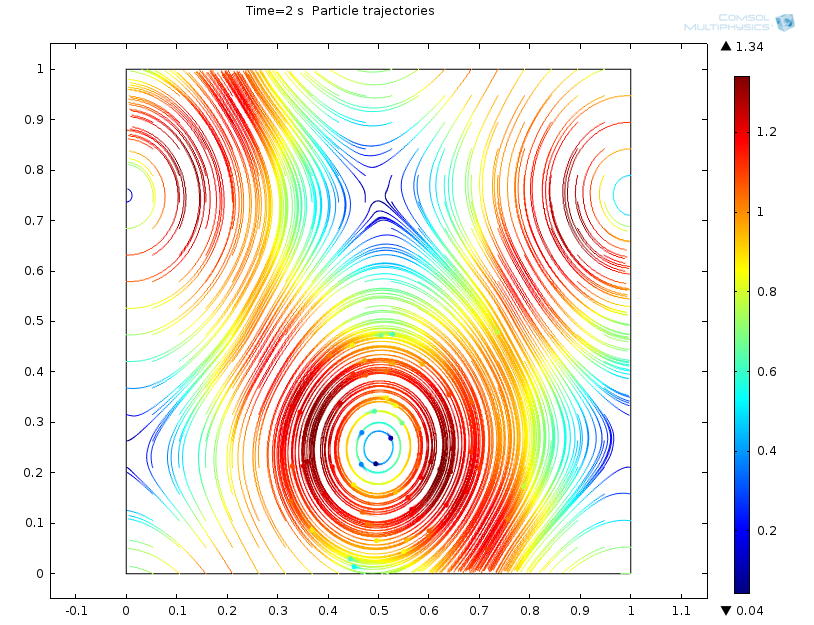
t=2s 时的粒子追踪结果。
下一步可能是确定停留时间,如果考虑大红斑,停留时间可能在 150~300 年间。



评论 (0)