
弹簧钩是一种在挂钩插入插槽时起固定作用的紧固件,常用于汽车工业。当我们设计弹簧钩时,分析挂钩在插入和拔出过程中的作用力是非常重要的。我们可以通过仿真来解决这个问题。
固定你的控制面板
汽车的仪表板可以为司机提供汽车车速、耗油量等有用信息。和仪表板本身一样重要的是它的安装方式。在许多工程案例中,弹簧钩被当作紧固件用于汽车控制面板的设计中,以确保不同的组件之间连接的安全性。
当在一个插槽中插入弹簧钩时,把挂钩插入和拔出插槽所需要的作用力是一个重要的考虑因素。利用 COMSOL Multiphysics 有限元分析软件,你可以研究这些作用力及其对挂钩产生的应力和应变。
将弹簧钩插入插槽
在弹簧钩模型中,由于弹簧钩结构的对称特性,我们只需对其中的一半进行分析即可。弹簧钩被假设为由具有各向同性硬化和恒定切线硬化模量特性的弹塑性材料制成,与之相对应,我们假定锁扣为刚性。当挂钩进入锁扣后面的空间,则意味着挂钩已被锁定。
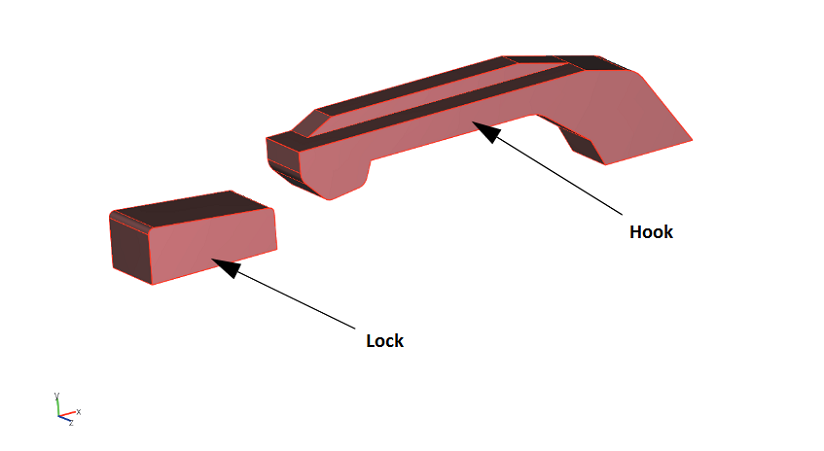
模型几何结构。
如下图所示,我们对这个模型施加了几个边界条件:对于对称平面,我们选用了一个对称边界条件。在锁扣表面施加一个固定边界条件,这个面是与另一部分的锁扣装置(在这里未建模)连接的位置。最后,对挂钩与剩余的几何结构的接触面施加一个指定边界条件。
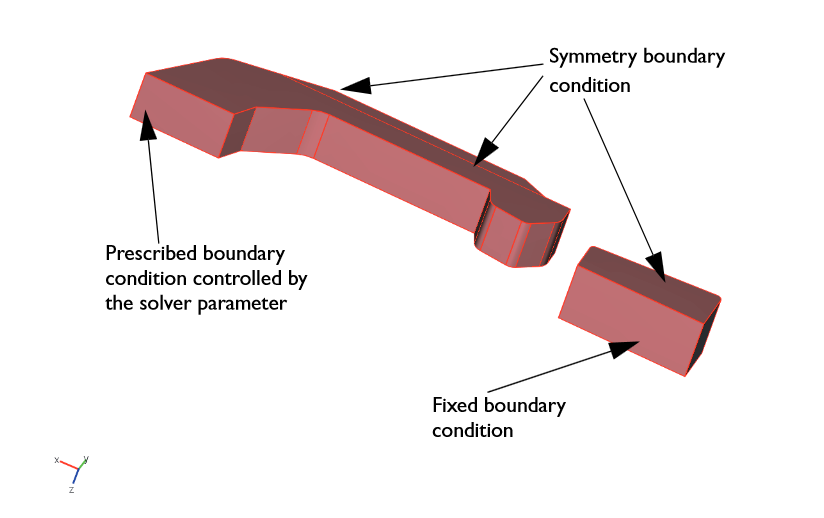
施加的边界条件。
评估应力和应变
在挂钩插入插槽之前,我们先来测试一下挂钩的有效应力大小。如下图所示,当参数为 0.84 时,有效应力达到峰值。这个参数表示挂钩插入插槽前的那一瞬间的位置。值得注意的是,挂钩在经过插槽边缘时,会向上弯曲。在挂钩完整插入插槽前,弹力对其施加一个压力,将其“按”入插槽。如果你用手握住挂钩,可以将其推至完整插入插槽前的临界点,然而此时,挂钩会被从你的手中拉开。
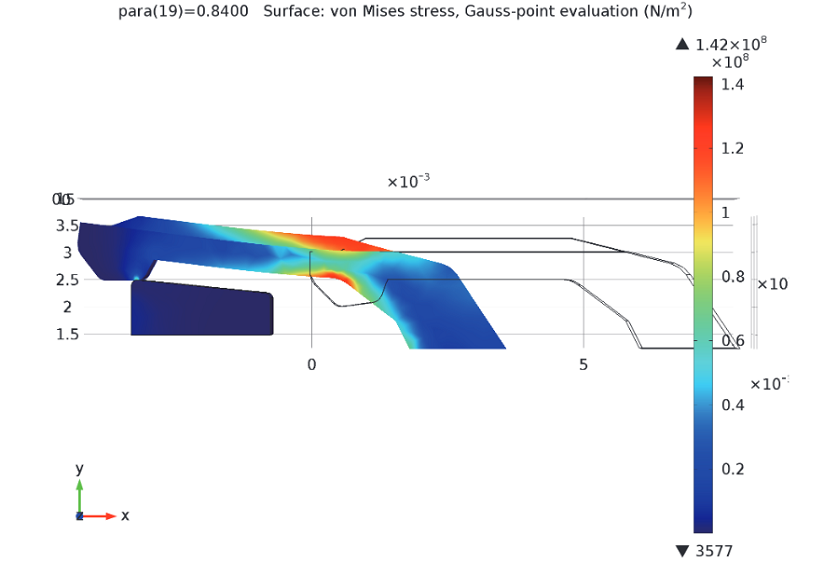
挂钩进入插槽前的有效应力水平。
下图显示了插入和移除紧固件所需要的力与参数之间的函数关系。当参数值从 0 变化到 1 时,挂钩以恒定的速度向内移动,最终插入插槽中。然后,当参数值在 1 和 2 之间时,挂钩被从插槽中拉出。
当参数值为 0.2 时,挂钩开始与固定的锁扣装置接触。此时挂钩的端部会受到急剧增加的、向上的作用力。实际上,当作用力达到峰值 2.5 N(参数为 0.23)时,挂钩便会卡到位。由于我们在仿真时控制了位移,故可以在整个过程中追踪力的大小。当参数值在 0.7 到 0.9 之间时,挂钩会从背面滑下。应力正负号的改变意味着挂钩实际上是被几何形变和弹性力的共同作用拉入插槽中。
当我们试图将挂钩从插槽中拉出时(参数值大于 1),我们必须施加一个三倍大的力(大约 7.5 N)才能将其拉出(参数值约为 1.12)。这是挂钩在锁定装制的设计中必须满足的因素。
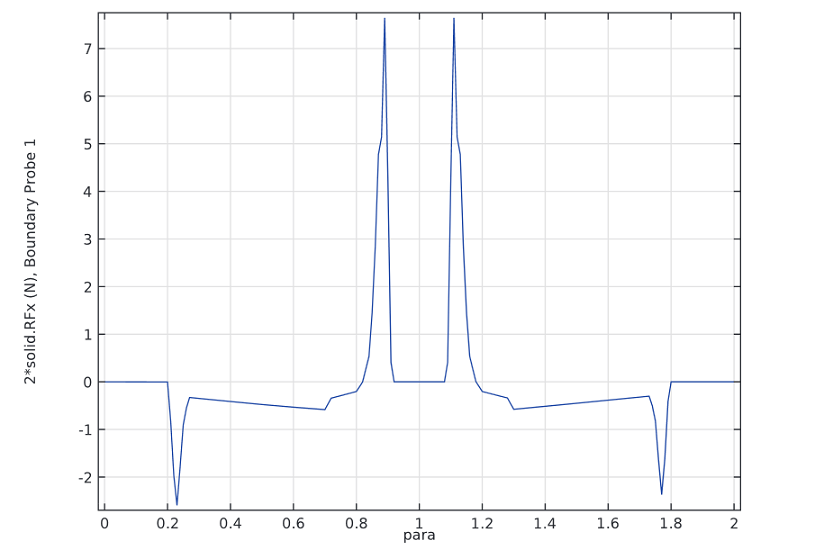
挂钩插入和移除插槽所需要的力。图中的第一个正峰值可以归因于完全插入插槽前,将挂钩推入插槽的弹性力。拔出时,挂钩碰到陡峭的表面,从而导致了图中第二个正峰值。当经过拐角时(参数为 1.2处),挂钩被自身的作用力压出,也就是图中的负作用力。
当挂钩从插槽中移除后,挂钩内部有塑性应变,如下图所示。因此,我们可以证明,当挂钩卡入插槽后,它的形变是永久的。
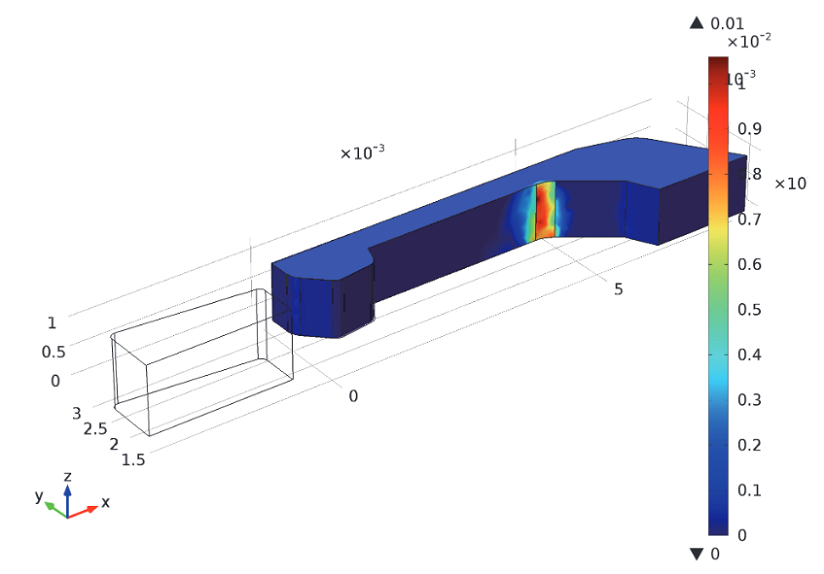
挂钩从插槽中拔出后产生的有效塑性应变。
结论
在本篇博客中,我们研究了仿真在分析挂钩插入和拔出插槽这一模型中发挥的作用。通过分析此类作用力,用户可以优化弹簧钩的设计,从而确保弹簧钩能提供持续的安全保障,同时保证在将其拔出时不会造成损坏。此类仿真特别适用于汽车行业中对汽车面板的重要部件进行维修和更换时的安全性分析。



评论 (2)
Deshuai Zhang
2023-05-23我在COMSOL和abaqus中构建了相同的网格,在线弹性假设下,设置COMSOL锁扣为刚性,abaqus为“硬”接触。所计算的结果不一致。在这种理想假设下,我认为计算公式不会有偏差。差别可能来自于对于接触面的判别算法上,请问可以获得接触判断或者点面离散(或其他)的相关算法文档吗。类似技术手册的东西。我在https://www.comsol.com/multiphysics中没有找到相关的介绍。
Anran Wei
2023-06-02 COMSOL 员工在COMSOL的这个案例中,是把锁扣设为了刚体,您可以检查下在其他软件中是否也设置为了刚体。您所说的其他软件中的“硬”接触,不涉及把某个接触的某个物体当成刚体的处理。若您想详细了解COMSOL中接触设置的原理,可以在软件中的帮助文档里查询,在Structural Mechanics Module-User’s Guide-Contact Analysis Theory目录下。