
假如您在骑自行车时有人从侧面推了您一下,为了尽快让自己保持平衡,您会往同一方向转动自行车车把以防止从自行车上跌下来。骑车的人会出于本能去这样做,但神奇的是,我们的自行车也能做到这一点。现代自行车的设计通常具有自平衡功能;当运动失控时,它们能很好地保持平衡。现在让我们一起来看看如何在 COMSOL Multiphysics 中模拟这种效果。
我们所了解的自行车自稳定性
自十九世纪八十年代安全自行车面世以来,现代自行车并没有从根本上发生改变。在一个多世纪后的今天,科学家们仍在试图找出使自行车保持自平衡的关键所在。换句话说,怎样才能使无人操控的自行车保持平衡并直立运动?大量的学术论文借助分析方程解释了自行车运动的动力学。由 Francis Whipple 撰写的一篇论文便是最早的代表性著作之一,他在该论文中推导出了一般非线性方程,专用于计算倾斜、无人自行车的动力学。
长久以来,人们一致认为自行车保持稳定的因素有两个:前轮的陀螺进动和主销后倾稳定效应(或称为轨迹量),这是前转向轴与地面接触在前轮触地点前方时产生的。最近,代尔夫特和康奈尔大学的一组研究人员(请参见参考文献 3)发表了一篇综合性评论,对 Whipple 自行车模型的线性方程做了详细阐述。他们使用自己的研究成果展示了自行车的自稳定性。该研究表明,这种现象并非仅仅是某个简单的原因引起的。而是多种因素的组合,包括陀螺效应和主销后倾稳定效应、自行车几何结构、速度及质量分布,都对保持无人操控自行车的直立前进发挥了作用。
受此项研究的启发,我们开发了多体动力学模型,来演示无人自行车的自稳定行驶情况。

自行车在不同时间实例的运动情况。
自行车多体模型
该教程自行车教程模型演示了无人自行车在平面上受到侧向力的扰动而在正行驶方向发生倾斜的运动情况。我们对分析进行了扩展,来研究当前进速度和前转向轴倾角发生变化时自行车的自稳定性。
要建立自行车模型,我们做出以下假设:
- 假设所有组件均为刚性。
- 所有接头均视为无摩擦。
- 建模时,假设自行车车轮与地面形成刀形触点。
- 为车轮施加纯滚动约束。
- 假设自行车在平面上移动。
- 该自行车模型假设具有无后座车架,通过在后车架上添加的质量来定义。
这辆自行车由四个刚性组件组成:后轮;后车架,包括无后座车架;前车架,包括车把;以及前轮。尽管车轮的厚度有限,但我们仍假设它与地面在一个点发生接触。后车架通过铰链关节连接到后轮。并使用另一个铰链关节来连接两个车架。此关节的轴形成了自行车的转向轴。第三个铰链关节用于连接前轮和前车架。
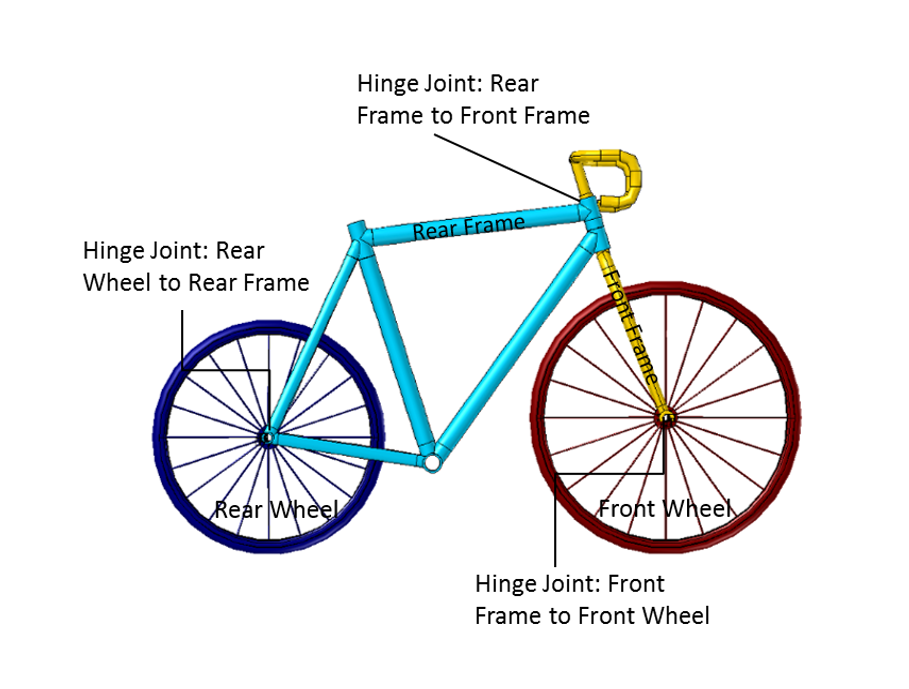
COMSOL Multiphysics 中的自行车几何结构。
本模型中使用的自行车几何结构如上所示。自行车组件的惯性定义取决于质量、惯性矩和质心位置。重要的几何参数包括车轮半径、轴距 (wb) 及转向轴倾角 (st)。转向轴倾角可以控制轨迹量 (c)。
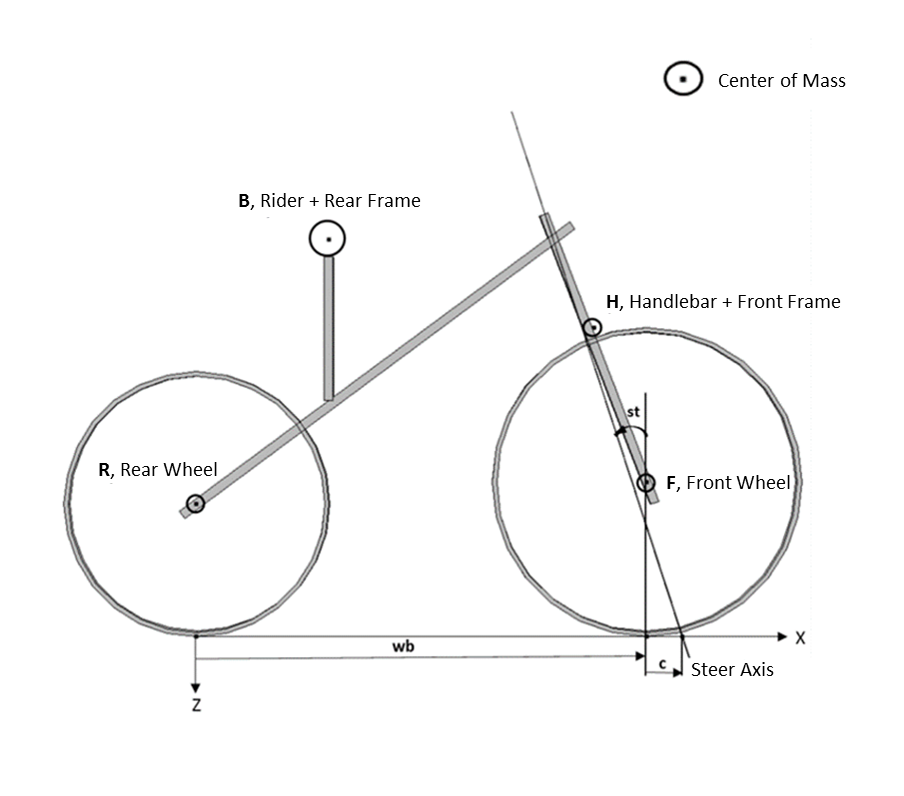
自行车示意图。
如上所述,假设车轮与地面之间是纯滚动运动。在纯滚动的情况下,自行车触地点的速度为零。在该模型中,车轮滚动时不考虑任何接触,以减少计算量。相反,我们使用另一多体动力学方法为该运动建模。为了描述车轮的偏航、倾斜及自转运动,我们创建了三个铰链及三个对应的无质量连杆。我们施加了三个无滑移约束来限制车轮在前进方向、面内横向及面外方向的滑移。由于无法对速度施加约束,我们将其转换成位移约束。
接下来,我们将描述设置这些约束的过程,相关内容也在Rolling of a Rigid Wheel 教程模型中进行了详细说明。
为确保车轮做纯滚动运动,需要三个约束来限制车轮在三个方向的滑移。
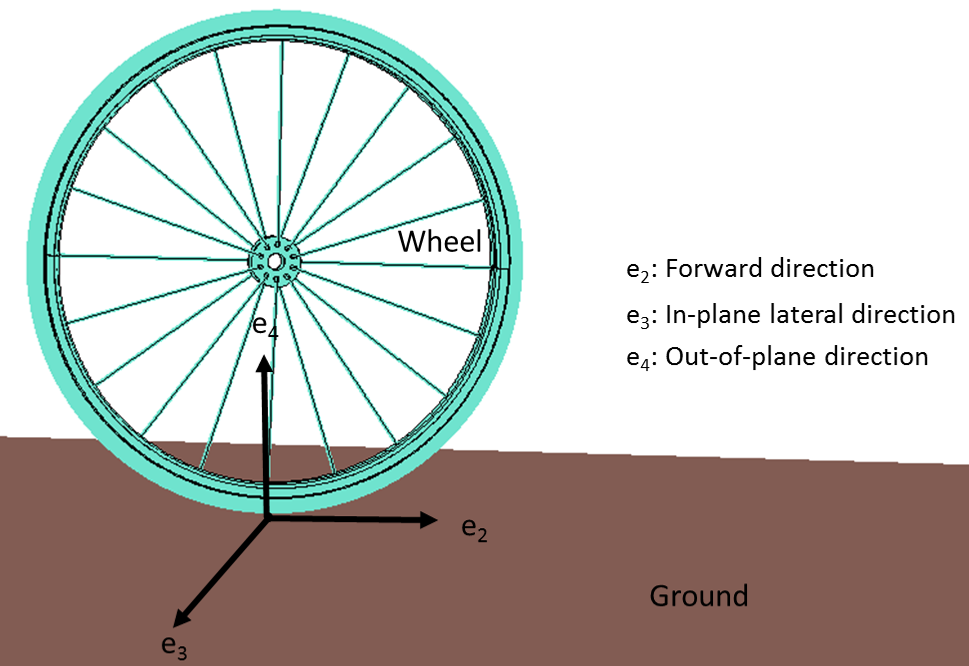
车轮模型,显示了三个约束方向。
这些约束如下:
前进方向无滑移:
面内横向无滑移:
面外方向无滑移:
其中,\bold{e}_{2}、\bold{e}_{3}和\bold{e}_{4}分别是瞬时前进方向(倾轴)、面内横向(旋转轴)及面外方向(\bold{e}_{4}=\bold{e}_{2} \times\bold{e}_{3});\frac{d\bold{u}}{dt}是重心的平移速度;r是车轮半径;\frac{d\bold{\theta}_{s}}{dt}是旋转角速度;且\frac{d\bold{\theta}_{l}}{dt}是倾斜角速度。
由于不能对速度施加约束,这些约束最终会离散,且实现方式如下:
其中,\bold{u}_{p}、\bold{\theta}_{sp}和\bold{\theta}_{lp}分别是上个时间实例的位移矢量、旋转角和倾角。
这些时间离散且无滑移的约束需要先前的车轮构型。刚体的平移、旋转和上一时间步中的瞬时轴均通过使用瞬态求解器中的全局方程和之前的解节点来存储。
自平衡自行车的运动仿真
我们选择了转向装置侧倾 18° 的自行车来进行本次分析。该自行车的初始前进速度为 4.6 m/s。1 秒后,自行车在很短的时间内受到 500N 的力扰动。这个力使自行车沿正向轴发生倾斜。
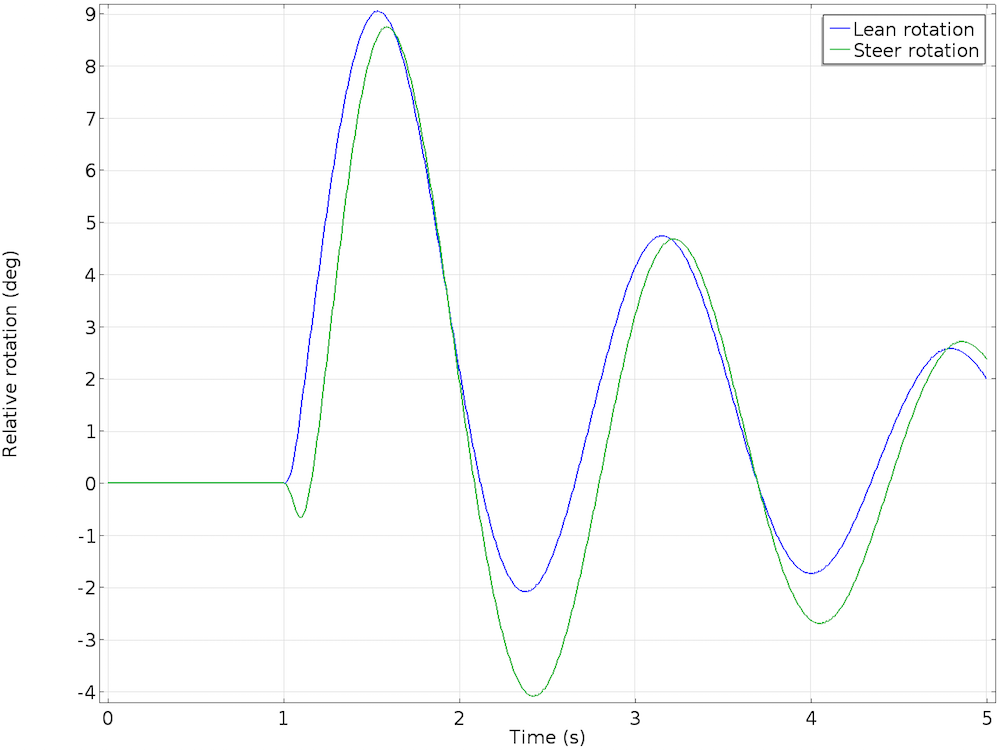
在第一秒内,自行车沿初始前进方向以恒定速度向前移动。接下来,侧向力使自行车开始倾斜。由于是无人自行车,因此不能人为干预使自行车保持平衡。那么会发生什么呢?我们观察到,当自行车开始倾斜时,车把开始朝着倾倒的方向发生转向。这个朝着倾倒方向的校正动作使自行车开始自我调整并趋于平直。
由于自行车在不同的前进轨迹上继续前移,它开始朝反方向倾斜。由于转向运动稍微滞后,几乎与倾斜同时发生,因此倾斜幅度较小。这种前后倾斜和转向扰动持续进行,最终阻止了自行车的倾倒。自行车直立向前移动,且前进速度略微增加。倾角和转向角以及角速度的振荡逐渐减弱并最终消失。
无人自行车在平面上绕前进轴倾斜时的运动情况。其中的箭头表示自行车的倾斜方向。
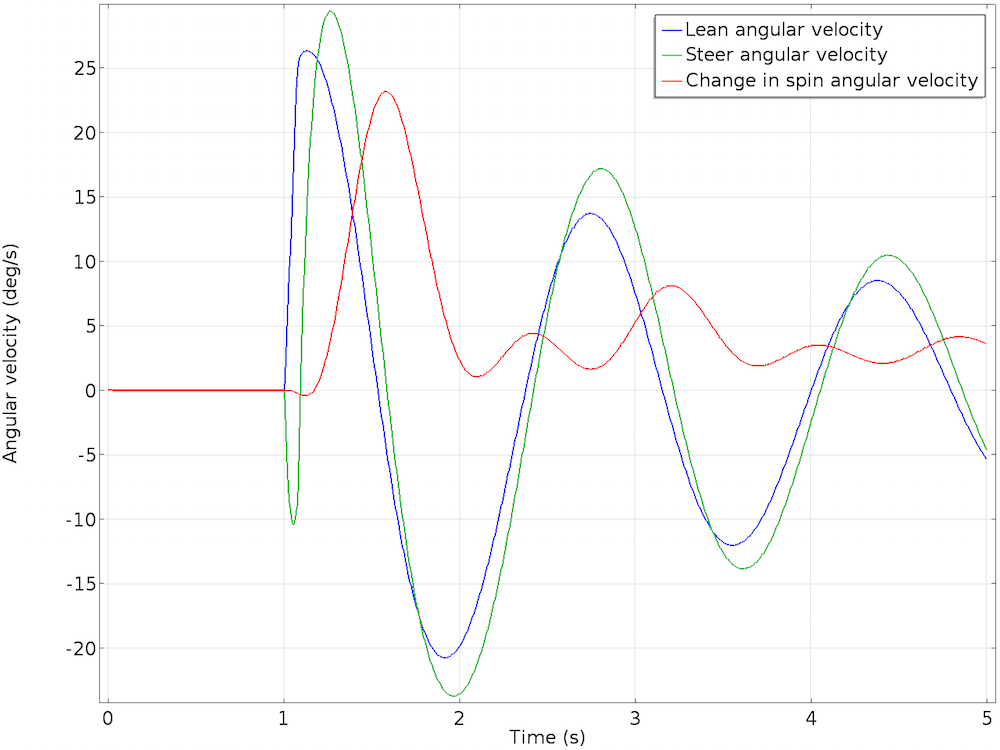
自行车倾斜和转向旋转的结果(左图)及相对角速度(右图)。
执行稳定性分析
到目前为止,我们已经了解自行车具有自稳定能力。研究表明,影响自行车稳定性的参数不止一个。自行车的几何结构、质量分布及前进速度均对其稳定性产生影响。要理解这一点,我们做了进一步的分析来研究两个参数的作用:初始前进速度和转向轴倾角。我们使用上述自行车模型作为参考构型,其转向轴倾角为 18°,向前行驶速度为 4.6m/s,并执行参数分析来研究这两个因数的影响。
初始前进速度变化
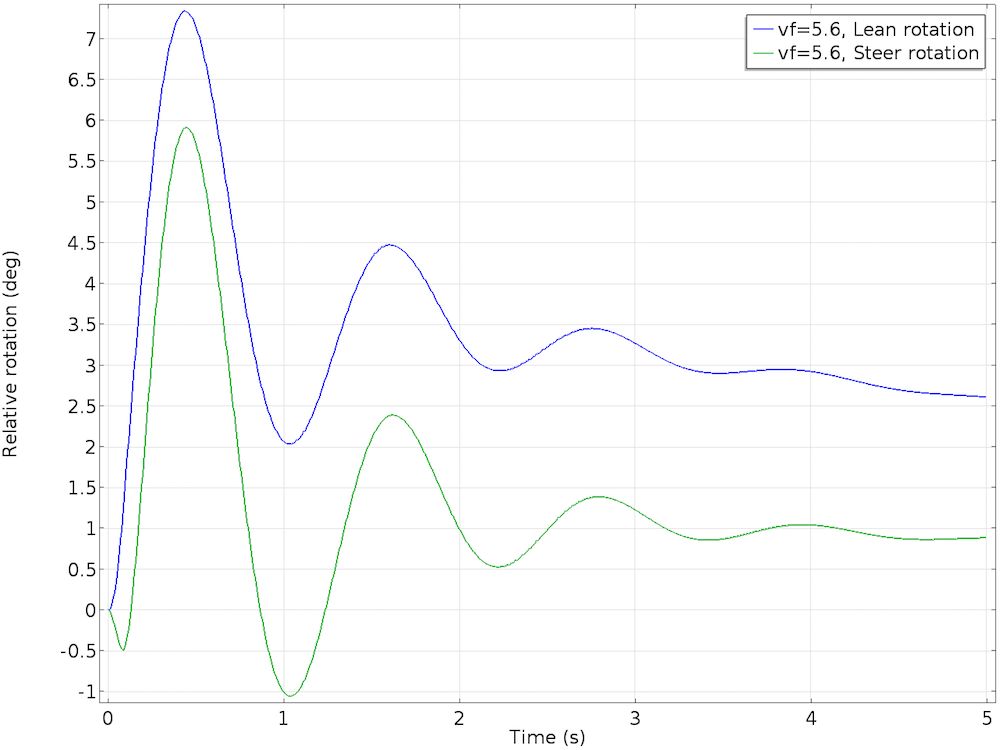
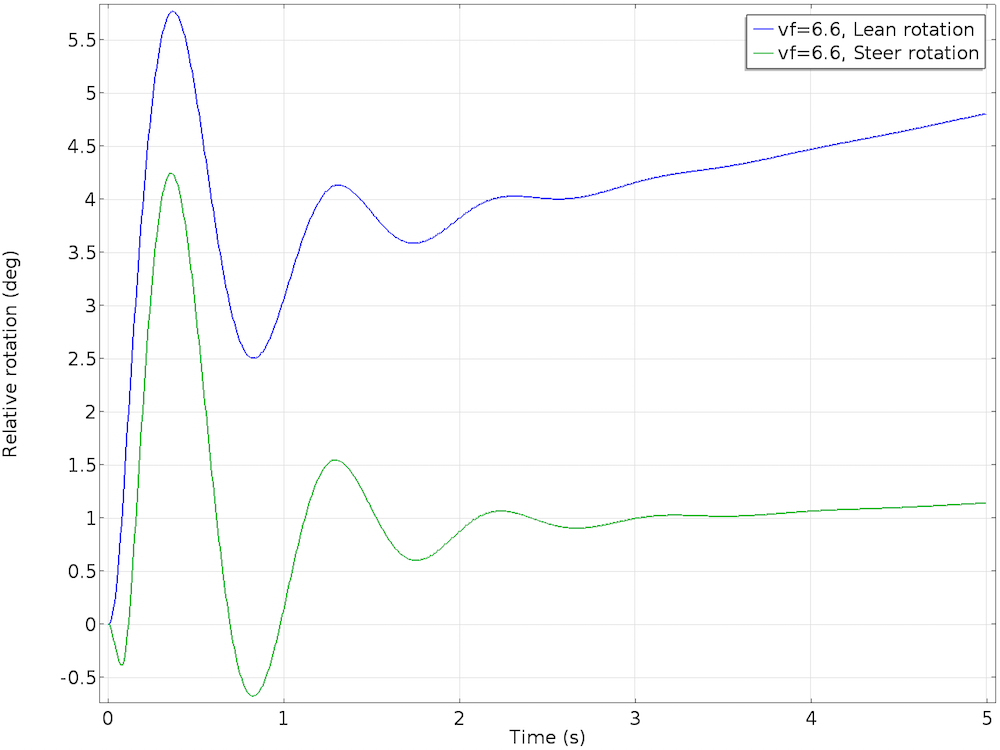
在静止状态下,自行车无法保持直立。为了研究自行车速度对自稳定性的影响,我们以 1m/s 的步长在 2.6m/s 到 6.6m/s 之间改变自行车的初始前进速度。在 2.6m/s 和 3.6m/s 时,自行车倾斜幅度非常大,不能保持稳定。在 5.6 m/s 时,自行车的倾斜速度减为零,但倾角是一个非零值。尽管这一构型稳定,但自行车仍会略微倾斜,并做圆周运动。在 6.6m/s 时,倾角和转向角会随时间的增加而变大,使自行车的运动变得不稳定。
| 不稳定 | 稳定 | 不稳定 | ||
|---|---|---|---|---|
| 2.6 m/s | 3.6 m/s | 4.6 m/s | 5.6 m/s | 6.6 m/s |
在稳定案例中,初始前进速度为 5.6m/s(左图);在不稳定案例中,初始前进速度为 6.6m/s(右图)。
转向轴倾角变化
转向总成对于自行车的自稳定性至关重要。如果自行车不能转向(例如,车把被卡住),则无法抵抗倾斜,因此会倾倒。对于这一点,转向轴倾角可以控制轨迹量,对自行车的自稳定性起着重要的作用。
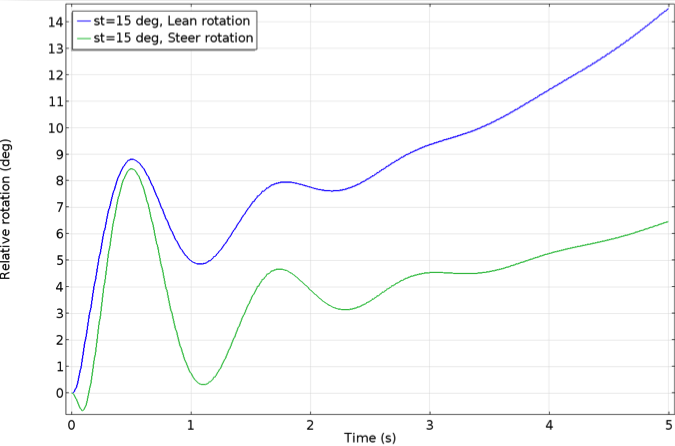
在本次分析中,我们以 1° 的步长在 15° 到 21° 之间改变转向倾角,从而改变轨迹量,以研究它对自行车稳定性所起的作用。在倾角为 15° 时,倾角和转向角继续随着时间的增加而变大,使该构型变得不稳定。自行车在 16°到 19° 的范围内能够保持稳定,而超过该角度范围时则不稳定。当转向倾角大于 19° 时,倾角和转向角会振荡,且振荡次数会随时间的增加而增加,使自行车变得不稳定。
| 不稳定 | 稳定 | 不稳定 | |||||
|---|---|---|---|---|---|---|---|
| Tilt | 15° | 16° | 17° | 18° | 19° | 20° | 21° |
| Trail | 0.066 m | 0.0706 m | 0.0753 m | 0.08 m | 0.0848 m | 0.0896 m | 0.0945 m |
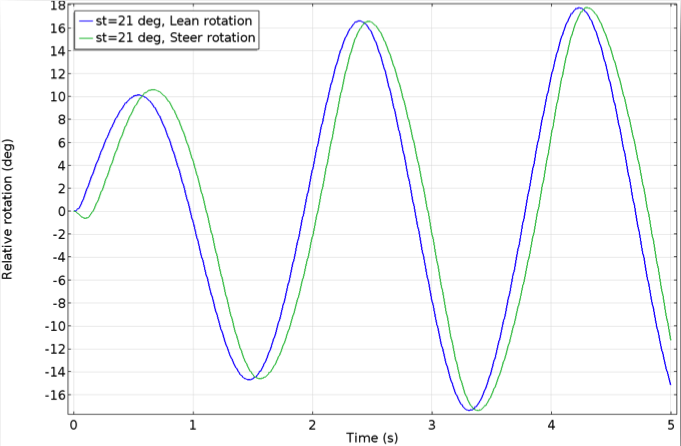
两个不稳定的案例,转向轴倾角分别为 15°(左图)和 21°(右图)。
关于使用多体动力学分析研究自行车自稳定性的结束语
在本篇博客文章中,我们描述了如何在 COMSOL Multiphysics 中通过“多体动力学模块”来模拟无人操控的自稳定自行车的运动情况。演示了如何通过方程在刚性车轮上实施无滑移的约束,并将这些约束与自行车多体模型进行耦合。然后,我们还分析了初始前进速度和转向轴倾角对自行车自稳定性产生的作用。通过计算这些参数,我们可以看到,在一种构型下保持稳定的自行车在其他构型中会变得不稳定。
自行车自稳定性同时受多个因素的影响。本次分析演示了自行车的自稳定性与它朝倾斜方向转向的能力相关,我们得出的结论与之前的研究完全一致。
扩展阅读
- 教程模型:Rolling of a Rigid Wheel
- 教程模型:Simulating the Motion of a Bicycle on a Flat Surface
- Meijaard, Jaap P., Jim M. Papadopoulos, Andy Ruina, and Arend L. Schwab. “Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review.” In proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 463, no. 2084, pp. 1955-1982. The Royal Society, 2007.
- 博客文章中:在瞬态模拟中使用之前的解操作



评论 (0)