如今,无论是创建身临其境的虚拟场景、设计舒适的室内声学环境,还是优化音频体验,室内声学仿真都是设计良好声效不可或缺的一部分。声学模块是 COMSOL Multiphysics®软件的附加产品,包含多个适用于室内声学仿真的接口。这篇博客,我们将重点介绍吸声边界条件对室内声学仿真的重要性。
吸声性能
为了理解吸声边界条件,我们首先来讨论吸声系数。使用以下三个量来描述吸声体的吸声特性(参考文献 1):
- 吸声系数,\alpha: 非反射声能与入射声能之比
- 比声阻抗,Z_{\rm n}: 声压与吸声体表面法向粒子速度之比
- 复压力反射系数,R: 反射声压与入射声压之比
以平面波进入多孔吸声体的理想情况来分析这些参数,具体如下图所示。
这里,假定空气和多孔材料的波数分别为k和k_{\rm e}。入射、反射和透射声压分别为p_{\rm i},p_{\rm r}和p_{\rm t}。入射角、反射角和透射角分别为\theta,\psi和\phi。入射声和反射声的振幅用A_{\rm i}和A_{\rm r}表示, 多孔介质中的正向声波和反向声波用B_{\rm t}和B_{\rm b}表示。假定厚度为dm 的多孔吸声体为等效流体(更多信息请参见Multiphysics Cyclopedia)。具有刚性边界的终端设置为x=d。
根据线性声波方程, 入射声、反射声和透射声在 x 方向上的粒子速度分别为v_{\rm i},v_{\rm r}和v_{\rm t}, 可表示为以下形式:
式中,Z_{\rm 0}和Z_{\rm C}分别代表空气和多孔材料的特性阻抗。根据定义,反射系数可表示为:
在空气层和多孔层(x=0)的界面边界上,存在以下两个连续条件:
根据这些连续条件和费马原理\theta=\phi,比声阻抗可由下式表示:
故,
吸收系数可通过下式确定。
因此,可以通过为边界施加三个量中的一个来模拟边界的吸声情况。同样,上述公式表明\alpha本质上与入射角相关,R和Z_{\rm n}是包含相位信息的复值参数,\alpha是能量参数。相位信息对于准确模拟室内模型非常重要。因此,复值参数通常是基于波的室内声学仿真的较好的输入参数。另一方面,吸声系数有利于直观地读取吸声体的性能,它是吸声测试的主要输出。随机入射吸声系数,即立体角的平均值,被视为吸声体的实际性能。
在下列公式中,我们将进一步研究多孔材料的声阻抗。
x=0处的传输压力和速度如下:
x=d处的传输压力和速度如下:
有了这些公式,我们就可以使用下列矩阵形式来表示入口处的参数和终端值:
p_{\rm t}(0) \\
v_{\rm t}(0) \\
\end{bmatrix}=\begin{bmatrix}
\cos{(k_{\rm e}d\cos\phi)} & j\frac{Z_{\rm C}}{\cos\phi}sin{(k_{\rm e}d\cos\phi)} \\
j\frac{\cos\phi}{Z_{\rm C}}sin{(k_{\rm e}d\cos\phi)} & \cos{(k_{\rm e}d\cos\phi) \\
\end{bmatrix}
\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}={\bm T}_{\rm F}\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}
式中,{\bm T}_{\rm F}是流体层的转移矩阵,已被广泛用于利用转移矩阵法(TMM)建立吸声和隔声模型(参考文献 2)。利用斯涅耳规则ksin\theta = k_{\rm e}\sin\phi,可以将{\bm T}_{\rm F}改写为下列形式:
\cos{(k_{\rm n}d)} & jZ_{\rm C}\frac{k_{\rm e}}{k_{\rm n}}sin{(k_{\rm n}d)} \\
j\frac{1}{Z_{\rm C}}\frac{k_{\rm n}}{k_{\rm e}}sin{(k_{\rm n}d)} & \cos{(k_{\rm n}d) \\
\end{bmatrix}
式中,k_{\rm n}=(k_{\rm e}^2-k^2\sin^2{\theta})^{\frac{1}{2}}。在终端 (v_{\rm t}(d) = 0) 的刚性边界条件下,可以计算出多孔吸声体的比声阻抗:
上式表明,特定声阻抗本身与角度有关。因此,要对边界上吸声进行完整仿真,应考虑吸声阻抗的角度依赖性。
局部反射和扩展反射模型
在建立边界吸声模型时,通常会采用两种吸声边界模型:局部反射模型和扩展反射模型。局部反射模型是室内声学仿真的标准模型,它使用与角度无关的阻抗(通常使用正常入射条件下的阻抗值)来描述边界的吸声特性。该模型假定吸声体表面某点的粒子速度与表面其他点的行为无关。扩展反射模型采用与角度相关的阻抗。当然,局部反射模型是近似模拟,但能准确高效地模拟声阻抗与角度关系不大的吸声体,如具有高流阻的刚性背衬多孔材料和带蜂窝芯的吸声体。扩展反射模型虽然精确,但通常需要对吸声体内部进行额外模拟。要实现准确高效的室内声学模拟,应为室内安装的吸收体选择合适的吸收边界模型。下文,我们将分别从理论和数值上来证明吸收边界类型对随机入射吸收系数的影响。
不同的表面模式如何影响吸声性能
我们计算了钢性背衬多孔吸声器和背部有空气层的隔音帘的吸声性能。将多孔材料视作厚度为 100 mm 的等效流体。采用经验 Miki 模型模拟流体特性,流阻为 13,900 Pa s/m2。由于所使用的隔音帘相对于研究频率的波长非常薄,我们使用了渗透膜模型,并将其与空气层耦合。使用渗透膜模型,可按下式计算吸声帘幕的传递阻抗:
式中,R_{\rm C}和M_{\rm C}分别代表流阻和表面密度分别设置为 416 Pa s/m 和 0.5 kg/m2。在理论研究中,我们使用了转移矩阵法,并将统计吸收系数作为随机入射值计算。统计吸收系数\alpha_{\rm s}的定义如下:
薄材料{\bm T}_{\rm T}的传递矩阵表示如下:
1 & Z_{\rm t} \\
0 & 1 \\
\end{bmatrix}
根据上述传递矩阵,可以得出含空气层的隔音帘的特定声阻抗:
对于转移矩阵法,可通过代入\theta=0来计算局部反射模型。
在数值研究中,我们计算了混响室吸声系数,即在混响室中测得的吸声系数。该系数值取决于测量的房间和样本大小。吸声系数早在 ISO:354 中就被作为一种标准测量程序,广泛应用于实际的室内声学设计中。
为了利用 COMSOL Multiphysics®有效模拟混响室吸声系数的测量,我们对带嵌入式吸声体的唯一硬质地板进行了二维模拟,如下图所示。
参考文献 3 中的验证研究表明,这一简化模型非常接近混响系数的测量结果。
我们使用压力声学,边界元接口模拟入射压力场和刚性地板,使用压力声学,频域接口模拟吸声体内部的压力。多孔介质声学功能用于模拟多孔材料。借助声学 FEM-BEM 边界功能,可以同时设置隔音帘的传递阻抗。对于局部反应模拟,禁用了吸声体域,将相应的法向入射声阻抗施加到吸声体表面。按照以下步骤计算混响室吸声系数:
- 对于入射角为\theta_n的平面波,计算吸声体表面入射的W_{{\rm i},\theta_n}和吸收的能量W_{{\rm a},\theta_n}。
- 使用下式计算总吸收能量与总入射能量之比。
混响室吸声系数\alpha_{\rm r}如下所示。
式中,N是入射角数。在数值试验中,使用背景压力场模拟平面波入射场,W_{{\rm i},\theta_n}和W_{{\rm a},\theta_n}由下式定义:
式中,p_0是入射压强的振幅,\bm n和{\bm I}_{\theta_n}是吸收体表面法线矢量和入射角{\theta_n}的声强矢量。
下图比较了多孔吸声体的随机入射吸收系数。局部反射和扩展反射之间的差异很小, 但可以观察到,尤其是在高频下。因此,如上所述,对于具有高流阻和刚性终端的多孔材料来说,局部反射模型似乎是一个很好的近似。
另一方面,如下图所示,隔音帘的随机入射吸收系数的比较显示出局部反射模型和扩展反射模型之间存在巨大差异。这是由于空气层具有很强的入射角度依赖性。这也符合传统规则,即对于含空气层的吸声体,扩展反射模型非常重要。
混响室吸收系数与统计值的比较
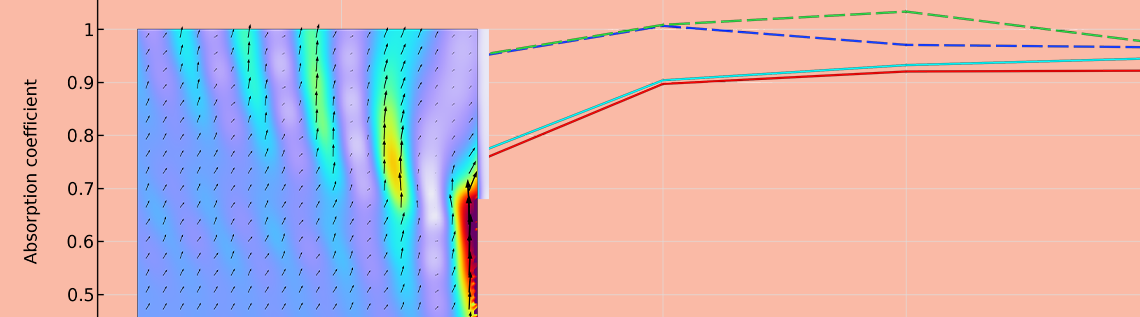
由上文的吸收系数图中可以看出,无论采用哪种吸声体和吸收边界模型,混响室的吸收系数都大于统计值,并超过 1(理想吸收以上)。这种现象被称为“边缘效应”,是实际测量中的典型现象,它是由刚性地板到吸声体表面的能量流动引起。下图入射角为 60°、频率为 500 Hz 的隔音帘扩展模型即显示了这种情况。此案例中的能量流动是由样本边缘周围的声压梯度引起的:地板附近的声压由于反射声的作用而变大,而吸声体前面的声压由于吸声效应而变小。能量流动发生在样品边缘,通过增大样本面积可以减小其对吸声系数的影响。因此,ISO:354 规定了测量混响室吸声系数的样本尺寸。
 入射角为 60°,频率为 500 Hz 时的振幅和用箭头表示的声强视图。
入射角为 60°,频率为 500 Hz 时的振幅和用箭头表示的声强视图。
结论
这篇博客介绍了边界吸声的理论知识,并探讨了吸声边界模型的类型如何影响吸声性能。对于室内声学仿真,COMSOL®中的射线声学、压力声学、频域和压力声学、时域显式物理场接口非常适用。射线声学接口基于几何声学,无法准确模拟声波的行为。然而,我们的模拟可以表征表面吸声器的入射-角度依赖性行为,有助于提高室内声学仿真的准确性。
基于波的方法可以准确模拟边界的吸声特性。多孔介质声学和内部阻抗功能可用于模拟吸声边界的扩展反射。压力声学,频域接口可以轻松处理这些条件, 因为该方法本身与频率相关。另一方面,扩展反射边界条件的时域建模非常具有挑战性,因为很难在时域中模拟吸声特性的频率依赖性。不过,我们可以在时域中使用多孔介质声学功能,模拟具有扩展反射的多孔吸声体。该功能的时域版本使用高效的辅助微分方程方法来考虑多孔材料的频率依赖性。因此,我们可以根据吸声体的配置灵活选择吸声边界模型。
在接下来的博客中,我们将使用时域多孔介质声学功能来探讨吸声边界类型的选择如何影响会议室的声学效果。
参考文献
- Z. Maekawa, J. H. Rindel and P. Lord. Environmental and Architectural Acoustics. CRC Press, 2010.
- J.F. Allard and N. Atalla. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials. Wiley, 2009.
- T. Sakuma, S, Sakamoto and T. Otsuru. Computational Simulation in Architectural and Environmental Acoustics: Methods and Applications of Wave-Based Computation. Springer, 2014.



评论 (0)