许多疲劳评估指标是基于应力评估的,然而,它们与高性能优化方法如基于梯度的优化不兼容,因此直接应用优化方法来改善疲劳性能具有挑战性。这篇博客,我们将介绍如何将应力最小化作为一种启发式算法来改善疲劳行为。该方法通过基于梯度的优化改善数千个设计变量,同时又能保持设计的质量和刚度特性。
理解疲劳
当一个零件受到反复加载的载荷时,材料中就会出现小裂纹。这些裂纹可能会随着每个载荷周期开始增长,直到快速进入扩展阶段,最终导致零件的结构失效。这种起始、扩展和最终失效的过程定义了疲劳断裂过程。实际上,在大多数情况下,目标是完全防止裂纹产生,因为一旦裂纹产生,控制其扩展阶段是一项艰巨的任务。疲劳分析的目标是计算出零件在发生裂纹之前所能承受的载荷周期数。这就是疲劳寿命的定义。

哈维兰彗星是一架飞机,由于它的窗户附近的冲压铆钉孔出现了疲劳裂缝而在飞行过程中解体。为了防止这种情况再次发生,后来的飞机采用了胶水连接的窗户。图片来源:Completeaerogeek。获得CC BY-SA 4.0授权许可,通过Wikimedia Commons共享。
疲劳裂纹的产生取决于零件上的载荷和载荷产生的应力。应该注意的是,疲劳裂纹可以在远低于材料屈服应力的应力水平下产生,并且反复加载的载荷是疲劳裂纹产生的主要驱动力。然而,从设计的角度来看,不考虑载荷的周期性行为,而是通过考虑静态载荷来确定高应力的区域是有用的。
应力最小化
最大应力的最小化是结构力学分析中的一个常见目标,但这种优化问题在实践中很难解决,因为最大应力的精确位置在优化过程中会发生变化。因此,通常使用近似最大应力的应力集中方法,特别是使用 von Mises 应力的 p 模来计算:
{max} \approx \left(\frac{\int_\Omega \sigma^Pd\Omega}{\int_\Omega d\Omega}\right)^{1/P}.
随着p\rightarrow\infty近似的准确性会提高,但也会导致梯度变化更快,从而导致数值问题。因此,很少使用大于 10 的值进行拓扑结构优化。不过,这篇文章的重点是形状优化,在不会引入数值问题的情况下有时可以使用大于 50 的值。近似最大应力\sigma_\mathrm{max},以及它的变体可以用来约束形状和拓扑优化中的应力,如 COMSOL 案例库中的飞轮厚度分布优化模型和具有最大应力约束的承载膝状结构的拓扑优化模型。接下来我们将介绍几个示例,来说明最大应力的最小化目标可以作为疲劳行为的形状优化的启发式算法。
支架的结果
第一个例子是用于演示结构力学中的各种概念的支架模型 (了解更多信息,请查看支架-疲劳评估应力优化模型)。下图显示了载荷、边界条件与应力分布。在固定孔上使用了弹簧以避免人为的应力集中。另外,该模型也可以扩展为包括螺栓的模型。
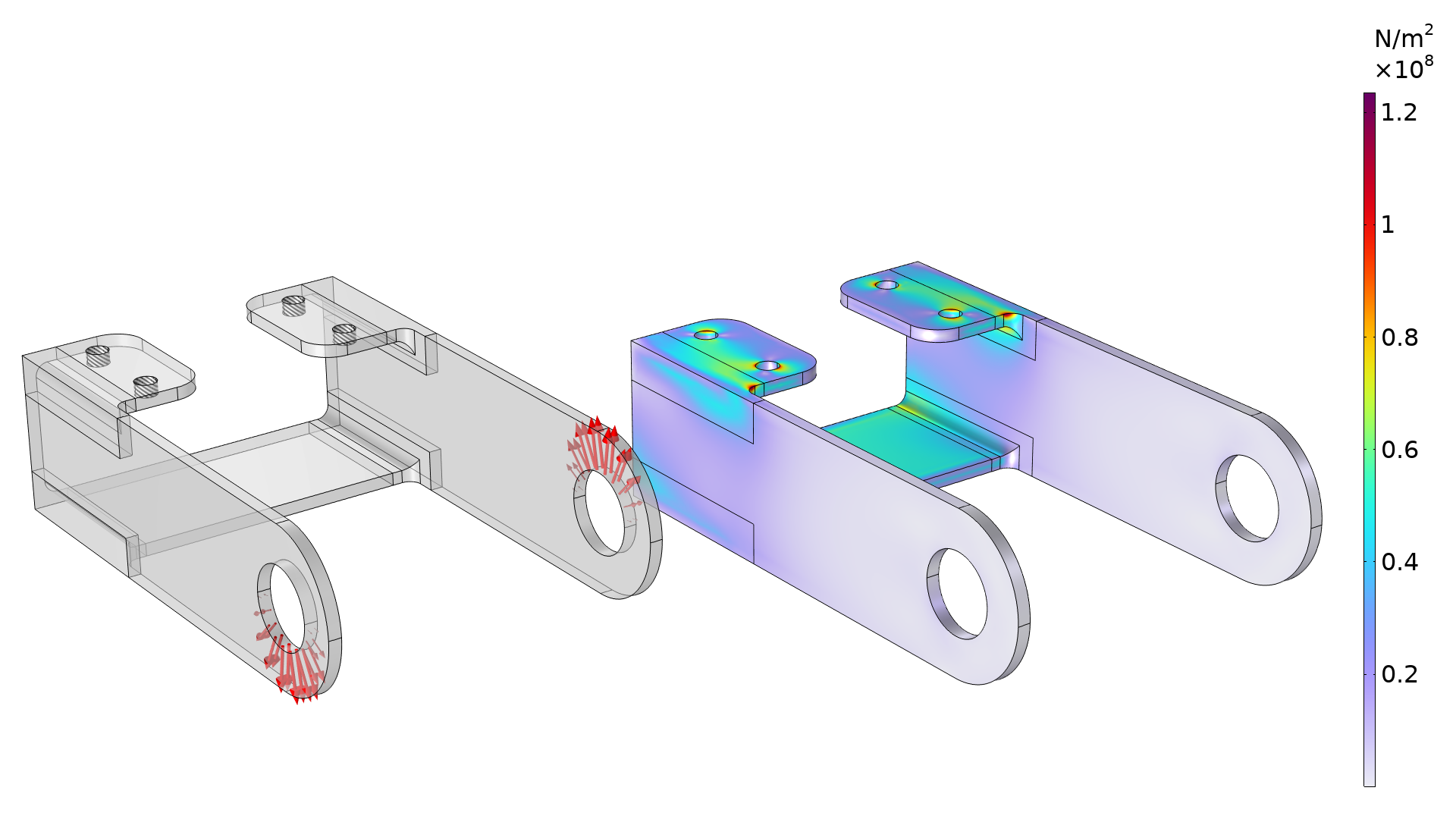
绘图显示了边界条件(左)和初始应力分布(右)。应力集中在支架顶部的圆角附近。
优化使用上一节中提到的 p 模(p=50)作为目标函数,但也加入了约束条件,以避免较重或刚度较低的结构。这里给出的 3D 示例使用了自由形状边界功能,但是 COMSOL Multiphysics®软件还有其他各种内置的形状优化功能,如博客文章电磁学中的形状优化:第一部分中所介绍的。使用自由形状边界功能可以改变有问题的圆角的形状,减少应力集中,从而改善疲劳性能(如下图所示)。
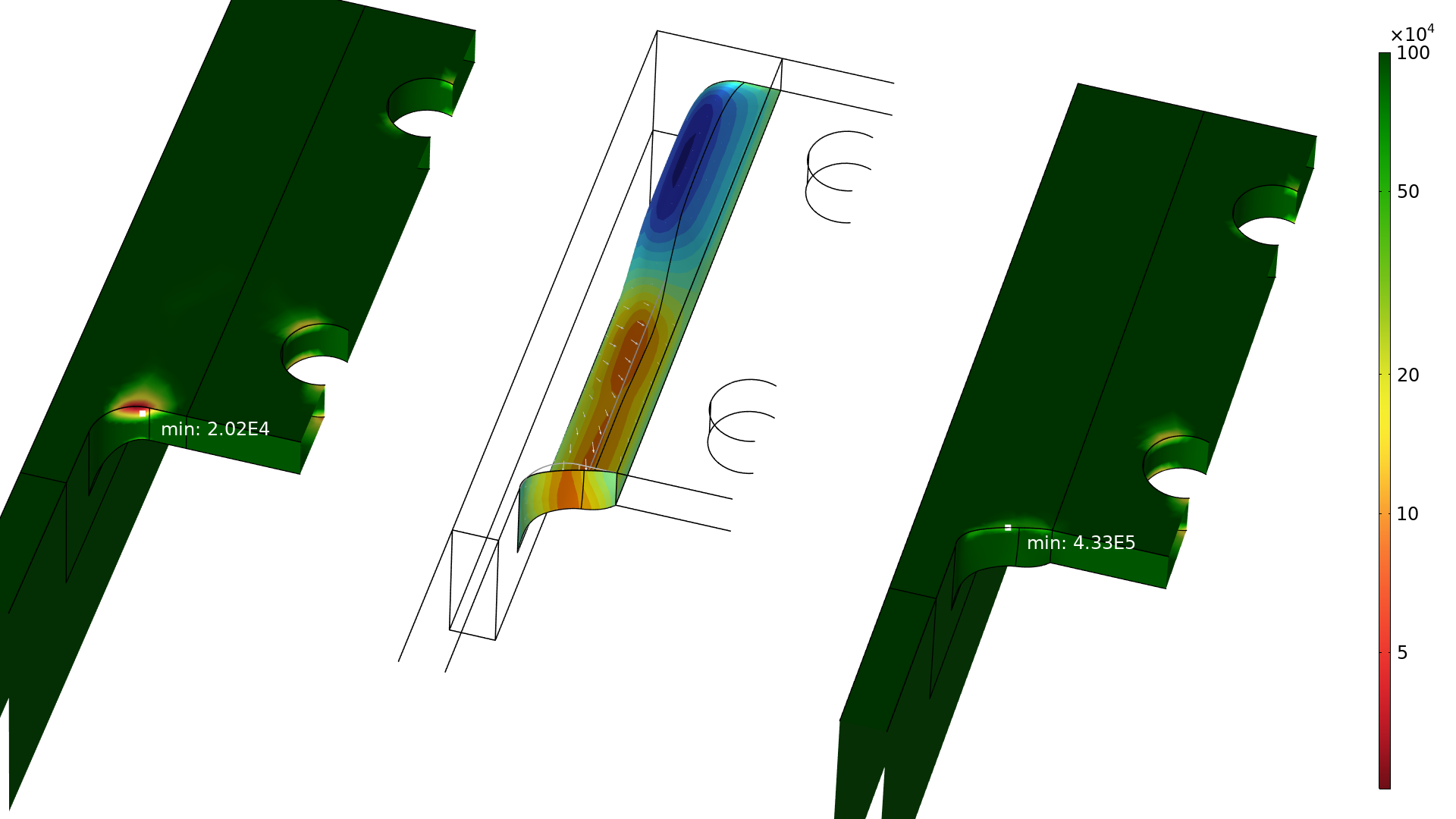
初始设计和优化设计(分别为左侧和右侧)的失效周期数切面图。形状的变化也用中间截面的箭头来说明,其中蓝色和红色区域分别对应于材料的去除和添加。
一般来说,只要一个部件的任何部分超过了疲劳寿命,它就会失效,所以导致失效的最小载荷周期数才是最有意义的数字。理想情况下,我们想直接使用这个数字作为目标,但这个数字和 p 模目标之间有很好的一致性,如下图所示。
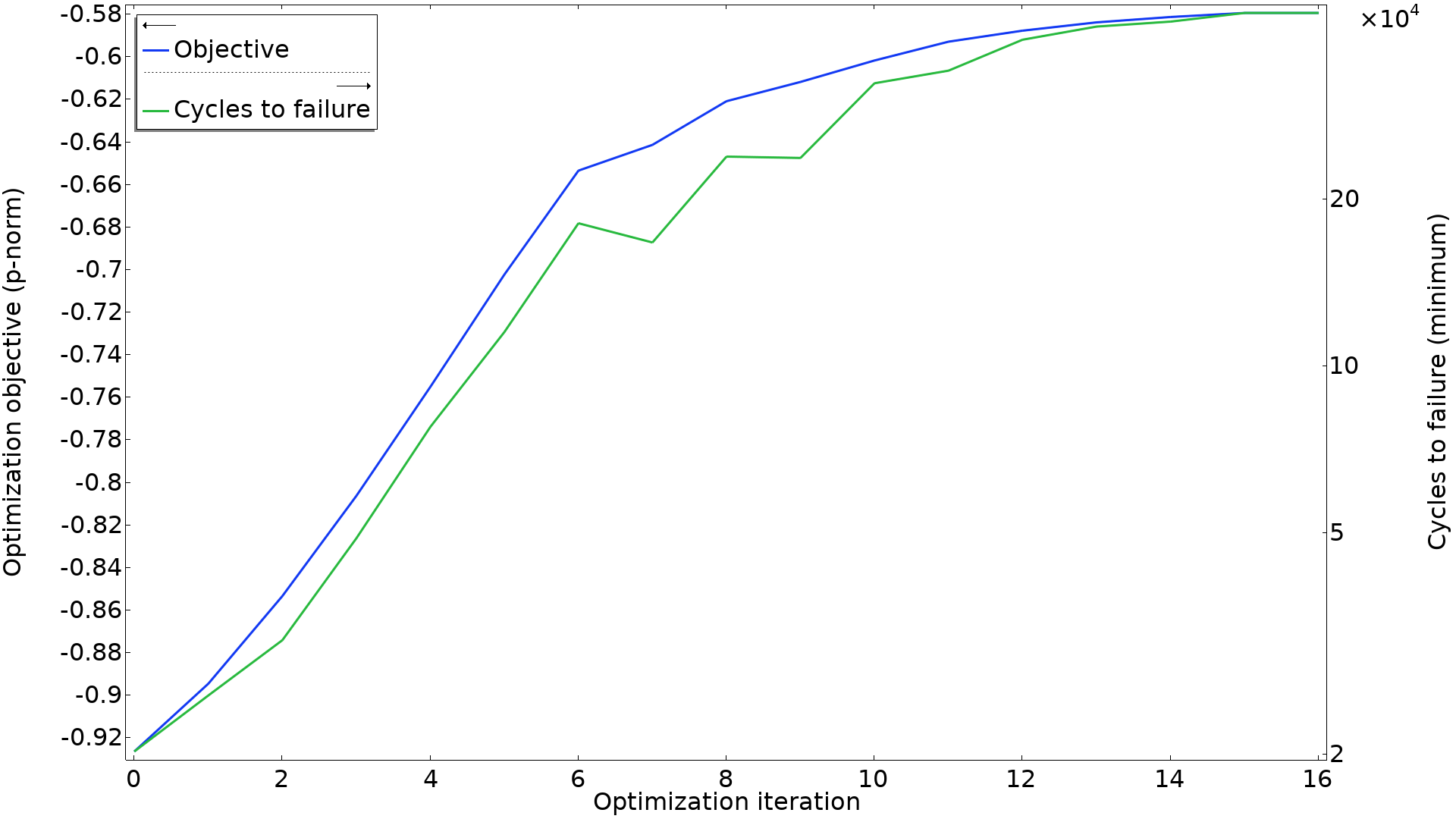
p 模目标与达到失效的最小周期数绘图。某些迭代数提高了 p 模值,但没有增加最小失效周期数,但这两者之间具有很好的相关性。
Von Mises 应力和疲劳寿命
怎么解释纯 Von Mises 应力最小化与疲劳寿命提高的相关性?一个部件的疲劳寿命受到许多因素的影响,其中应力幅值是主要的影响因素。疲劳寿命也受到平均应力的显著影响。在载荷正向和反向的应力均值为零的常见情况下,各处的平均应力均为零。
通常情况下,疲劳裂纹源于应力集中的自由表面。在自由表面上,主要是平面应力状态,但在实践中,通常可认为应力状态接近于单轴应力。这意味着,例如,第一主应力和 Von Mises 等效应力将是相同的。
对于混合应力的情况,即由静态载荷提供平均应力和另一个载荷提供脉动载荷的案例,这种方法不一定是最优的。但即使如此,也有很大的成功机会,因为在应力集中的地方,不同类型的外部载荷通常会导致相似的应力模式。
轮辋的结果
第二个例子是轮辋,来自轮辋-带疲劳评估的应力优化模型。这个模型在概念上与支架相同,除了以下四个点:
- 有几个载荷的情况下,疲劳分析寻找最差的组合(使用 Findley 准则),所以预计与最大应力的关系较弱。
- 实际上,载荷更多也会导致更多的约束。
- 扇形对称是为了进行形状优化而强加的(不是物理上的)。
- 在结果中使用疲劳使用因子(而不是疲劳寿命),这可以被认为与安全系数有倒数关系。
轮辋的几何形状、约束条件和边界条件如下图所示。螺栓使用了简单的固定边界条件,引起人为的应力集中,所以这些区域被排除在疲劳分析之外。
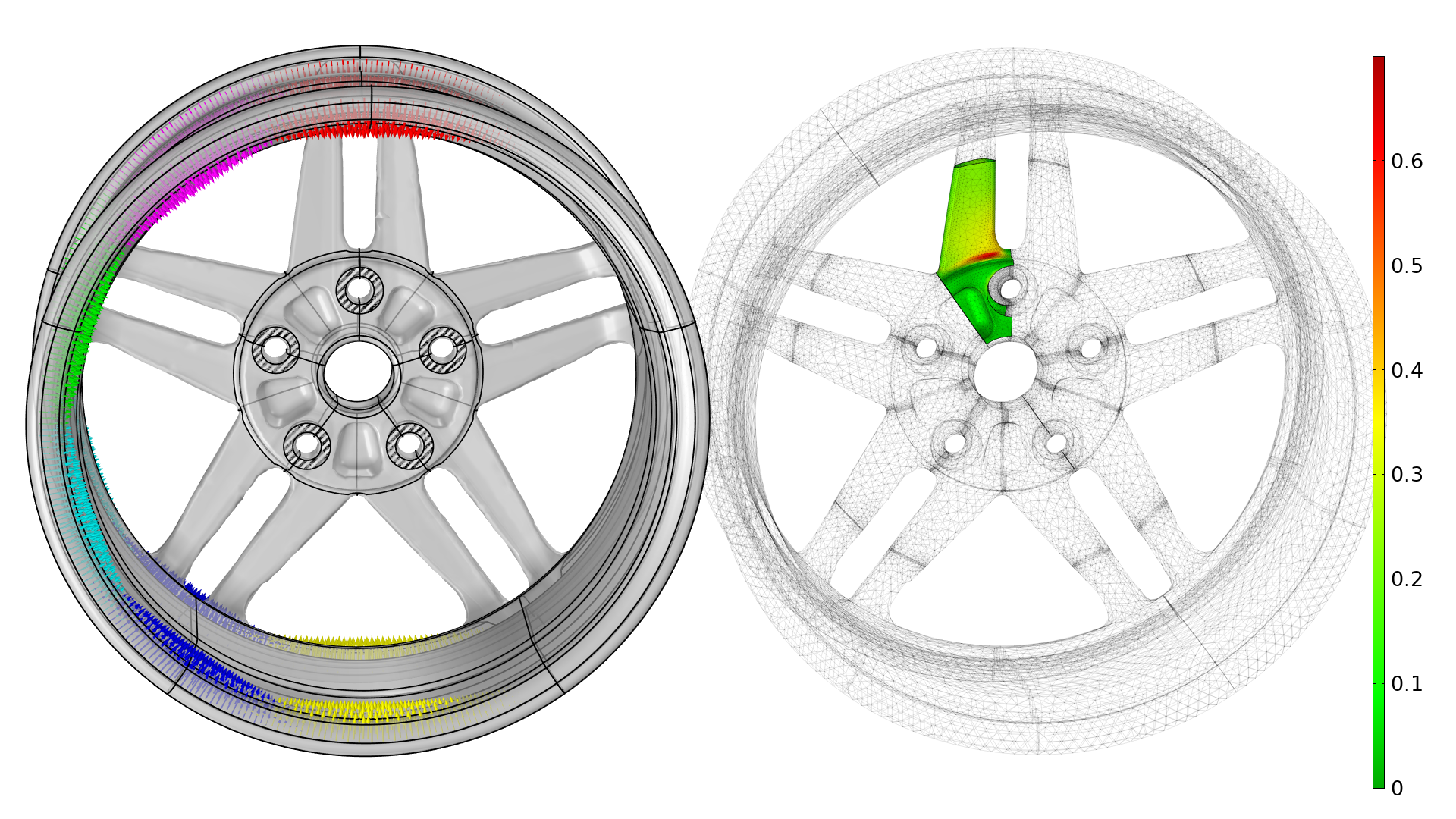
用不同颜色的箭头表示(左边)不同的载荷工况。右图绘制了初始疲劳使用因子,该图考虑了所有的载荷工况,对应一整圈车轮。注意,粗大的网格可以用在辐条上,但不能用于疲劳或应力评估。车轮还受到来自轮胎内气压的载荷,但图中没有考虑。
优化仍然使用 p 模目标(p=20)以及对质量的约束,但是这个例子考虑了更多的载荷工况,所以有更多的约束。下图说明了优化如何通过修改圆角来提高疲劳寿命。

初始设计和优化设计(分别是左边和右边)的疲劳使用因子切面图。箭头表示说明了中间切面的形状变化,灰色和黑色的线分别表示初始和优化的几何形状。
在这个例子中,p 模目标和失效前的最小周期数之间也有很好的相关性,从下图中可以看出。值得注意的是,其中两个载荷工况在 p 模方面占主导地位,但所有的约束条件在整个优化过程中都保持激活。
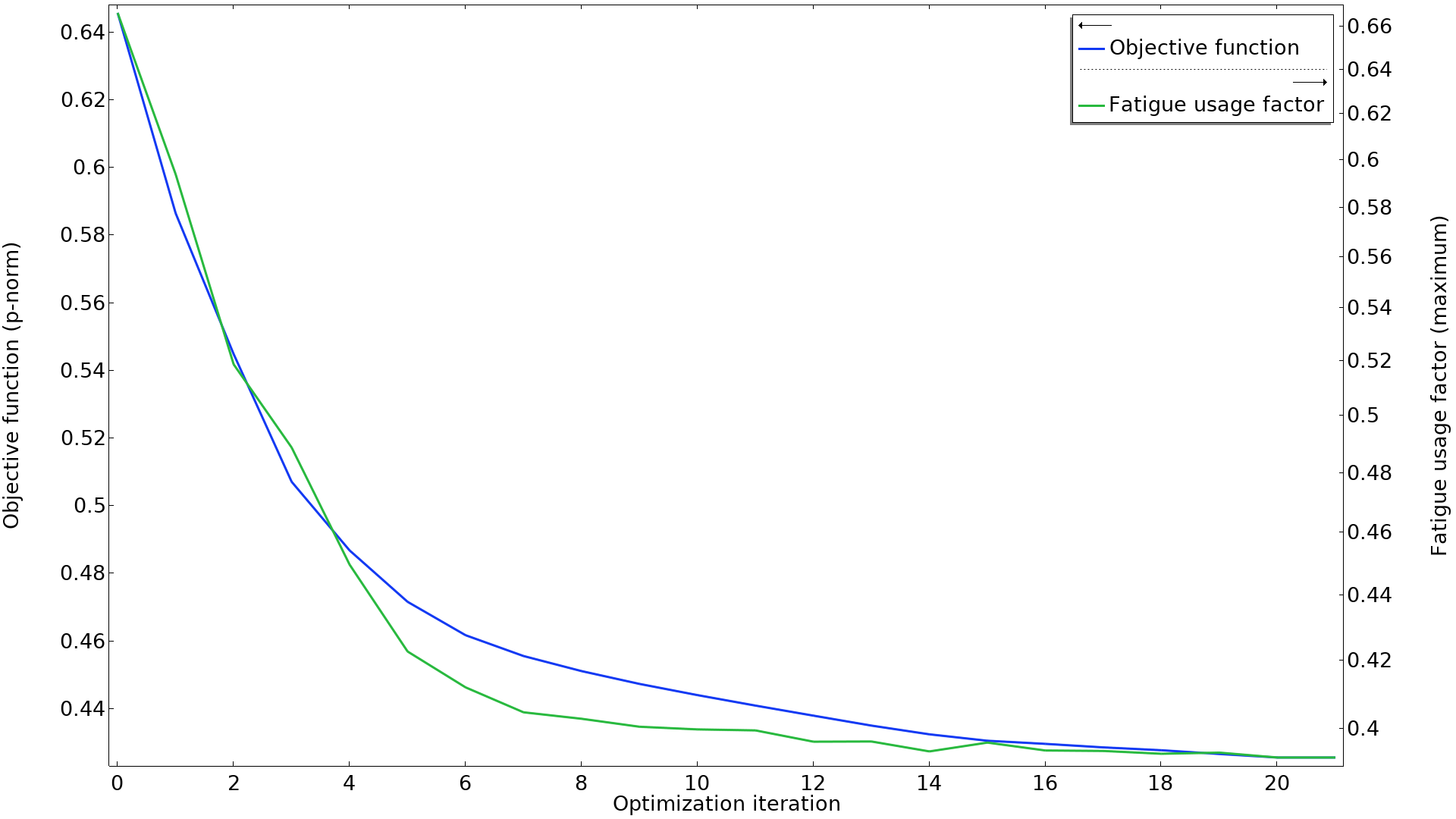
p 模目标与最大疲劳使用因子绘图。这两条曲线似乎具有很好的相关性。请注意,疲劳使用因子是在对数轴上绘制的。
结语
疲劳寿命的优化并不简单,但使用基于应力的形状优化通常可以改善疲劳行为。优化的结果应该用疲劳分析来检查,并且可以作为工作流程的下一阶段的输入。
在这篇博客中,我们重点使用 Von Mises 应力的 p 模作为目标,但由于 COMSOL Multiphysics®自动执行基于梯度的优化所需的敏感性分析,因此也可以很方便地使用其他物理量作为优化目标进行试验。



评论 (0)