AC/DC 模块 – COMSOL 博客 -

模拟质子疗法中的笔形束扫描喷嘴

Thu, 06 Mar 2025 05:31:35 +0000

质子疗法是一种利用高能质子束将电离辐射输送至治疗区域的先进癌症治疗手段。质子束的强度、方向和形状均需要精准控制，以向肿瘤区域输送适当的剂量，同时最大程度地减少对周围健康组织的损伤。这篇博客，我们将演示如何使用 COMSOL Multiphysics^® 软件模拟笔形束扫描喷嘴，用于将质子束精准地引入治疗区域。

质子疗法的优势

与其他形式的放射疗法相类似，质子疗法利用电离辐射破坏肿瘤细胞的 DNA 治疗癌症，这种辐射损伤会中断肿瘤细胞的繁殖，并最终消灭它们。在质子疗法中，电离辐射源是由粒子加速器产生的高能质子束。

使用质子束代替传统 X 射线的主要优势在于其明显的布拉格峰。通常情况下，后者的辐射剂量在浅层组织区域附近最大，并随组织深度单调递减，这意味着在治疗过程中，浅层和深层的健康组织也会受到次级照射。相反，质子会在停止前（即接近其最大穿透距离时）释放最大剂量，使浅层健康组织受到的剂量相对较小，而深层组织则完全不受影响。通过微调治疗计划中使用的质子束能量，医学物理专家可以确保质子束在肿瘤区域产生均匀的剂量，同时不伤害邻近的健康组织。

质子束和 X 射线束的剂量与穿透深度的关系，请注意质子束明显的布拉格峰。图片获 GNU Free Documentation License 许可，通过 Wikimedia Commons 共享。

质子束的横向剖面也需要加以控制，以使其与肿瘤的形状相匹配，最常见的两种方法是被动散射和笔形束扫描（PBS）。被动散射法利用一个或多个散射箔片来分散质子束，使目标区域（也称为治疗场）接受几乎均匀的照射。相比之下，笔形束扫描或点扫描则是将治疗场划分为类似体素的子区域，并利用狭窄的“笔形”射束对每个子区域进行治疗。

质子束的控制

质子束的导向由笔形束扫描喷嘴系统控制。最简单的笔形束扫描喷嘴由两块垂直和水平排列的偶极磁铁组成，以产生均匀磁场，分别使质子束向水平和垂直方向偏转。通过控制驱动磁铁的电流，辐射技术人员可以调整磁场强度，从而控制质子束的偏转程度。

笔形束扫描系统的数值模拟源于人们对磁共振成像（MRI）实时监测治疗（也称为磁共振引导质子治疗）的关注日益浓厚。笔形束扫描喷嘴和 MRI 系统都利用了强磁场，因此必须透彻地了解这两个系统之间的电磁相互作用，以决定采用什么必要的干预措施，确保 MR 成像和质子束的质量。

笔形束扫描喷嘴的 3D 模型。

笔形束扫描仿真

这篇博客，我们只研究笔形束扫描系统。所研究的模型由四个分离的功能磁体（两个偶极子和两个四极子），一个射束孔径和一个代表治疗场的靶平面组成。

笔形束扫描喷嘴模型的一部分。磁体系统包括两个标有 Q1 和 Q2 的四极子、一个垂直扫描偶极子 (SV) 和一个水平扫描偶极子 (SH)。图中还显示了射束孔径和靶平面（治疗场的位置）。

四极子旨在塑造质子束剖面的形状，以确保质子束与上游加速器束线（未模拟）相匹配。线性磁场梯度的作用是使质子束在一个横向方向聚焦，并在另一个方向散焦，因此需要两个四极子。聚焦的强度由输入的四极子电流控制。

沿四极子 1 (Q1)横截面中心的磁场。注意中心附近的磁场箭头方向。Q1 磁场在垂直方向聚焦质子束，在水平方向散焦质子束。另一个四极子（Q2）旋转了 90 度，其行为与Q1相反。

两个四极子的下游是两个扫描偶极子。这些磁体在极子间隙内产生恒定均匀的磁场，使质子束偏转到所需的目标位置。水平/垂直偏转的大小由磁场强度决定，而磁场强度又由输入偶极子电流的控制。在模型中，用户可以指定治疗场中所需的 (x, y) 目标位置，并根据给定的束流能量近似计算出所需的线圈电流，通过直接调整线圈电流就可以更精准地控制质子束的目标位置。

左图和右图分别显示了垂直扫描偶极子（SV）和水平扫描偶极子（SH）的磁场。

两个扫描偶极子的下游是束孔径和靶中心，前者是 PBS 喷嘴物理结构中唯一需要模拟的部分。为能够清晰演示，模型中还省略了喷嘴物理结构的其他部分，但在综合研究中可将它们包括在内。

为了可视化质子束轨迹，使用了 带电粒子追踪 接口模拟。磁场分布被无缝集成到粒子追踪模拟中，以准确模拟质子束的轨迹。（请注意，为了演示简洁清晰，模型中忽略了散射。）质子束的动能通常在 MeV 范围内变化，也被作为模型参数考虑在内。

分别沿 yz 平面和 xz 平面的质子束轨迹图（红色）和磁通密度模图。

上图描述了质子束和磁场的配置，质子束在靶平面上的标称位置为 x = 12 cm 和 y = 8 cm。

动手尝试

有兴趣尝试自己动手模拟本文中演示的多物理场模型吗？点击下方按钮，获取模型 MPH 文件。

获取模型

延伸阅读

阅读下列博客，了解仿真如何推动医疗保健领域的其他治疗方法：

]]>

模拟螺栓连接处的电接触电阻

Mon, 16 Dec 2024 02:10:42 +0000

随着 COMSOL Multiphysics^® 软件 6.3 版本的发布，固体力学 接口新增了 内部接触 边界条件。该边界条件简化了设置结构力学问题时的工作流程，并且在多物理场仿真中（尤其是求解电磁场时）具有优势。这篇博客，让我们通过计算交流母线板之间螺栓连接的电气接触，来看看新的工作流程和使用该边界条件的优势。

螺栓母线板模型的接触条件

考虑两个铜母线板之间的螺栓连接，电流为 1 kA，频率为 60 Hz。螺栓由钢制成，当拧紧螺栓后，母线板之间的配合面会产生很高的接触压。此接触压降低了两个铜板之间的接触电阻，因此电流将主要流经接触区域。然而，当交流电流通过导体时，由于存在集肤效应，电流将被迫流向导体的外部边界。这两种现象会产生相反的效应，这正是我们希望通过仿真来表征的行为。

两个铜母线板之间的螺栓连接。电流的电阻（蓝色箭头）取决于螺栓的拧紧程度。对称平面以灰色标出。

结构仿真问题

我们的方法首先假设两个母线板和螺栓之间的相对位移不大。也就是说，假设结构性能或电气性能只受接触压力的影响，而不受接触面相对运动的影响。根据此假设，我们可以将问题视为几何线性问题，因此无需考虑域的形状或方向的变化，这意味着我们可以使用 内部接触 边界条件。

内部接触 条件的应用优势在于它可以与 形成联合体 几何体定型步骤方法结合使用，而不是 形成装配 方法。使用 形成联合体 方法的结果是，网格本身在所有边界上始终是连续的，即使计算得到的位移场在边界上可能并不连续。这种方法的优势在于它减少了接触搜索算法的计算成本。不过，仍然有必要对这一接触区域的网格进行细化，因为我们希望获得界面处应力的良好分辨率。

两个母线板之间的接触区域使用的网格图像。

注意：如果使用 形成装配 几何定型方法，它将自动识别所有配合面并创建 接触对。然而，这种工作流程需要额外的设置和求解成本。形成装配 方法的优点是允许任意滑动和较大的相对变形。

了解更多信息，请阅读 COMSOL 学习中心的文章：结构接触建模指南。

除了 内部接触 边界条件，固体力学 接口还包括 螺栓预紧力 功能。在模型中，我们在一个简化的直通螺栓几何形状中应用了此功能。有很多方法可以模拟这种螺栓连接，本文使用的方法假定螺栓头、螺母和母线之间的场是连续的。该模型还使用了一个 热膨胀 功能（线性弹性材料 节点的子节点），用于计算由于钢螺栓和铜母线板的热膨胀系数不匹配而产生的应力。在此示例中，我们假设组件是等温的，这在许多工作条件下都是合理的，因为铜是非常好的热导体。

利用中心平面的对称性，我们可以进一步简化所考虑的情况。首先求解螺栓预紧力，然后求解由此产生的变形和应力，这样就可以直观地看到接触压力。与预期相符，接触压力以螺栓为中心向周围逐渐减小。正是这种接触压力会影响母线之间的电阻，接下来我们将在电磁模型中考虑这种现象。

螺栓周围接触压力大小的可视化。

电磁仿真问题

在此，我们特别关注接触区域周围在交流激励下产生的集肤效应或感应电流。这类分析需要使用 磁场和电场 接口，该接口包含一个 电接触 边界条件，可以模拟导体之间边界的电阻损耗。该边界条件作为 磁连续 边界条件的子节点应用，后者可确保磁场的连续性。磁场和电流在边界上都是连续的，但由于接触电阻的存在，边界上会有电场。接触电阻可以通过 Cooper–Mikic–Yovanovich 相关性或 Cooper–Mikic–Yovanovich 弹性相关性计算得出，这两种相关性都将 固体力学 接口 内部接触 功能的接触压力计算作为输入。

使用 磁连续 边界条件时，建模域内任何与该条件选中的边界所相邻的边界也必须应用 磁连续 边界条件。也就是说，在建模空间内，磁连续 边界中的每一条边都需要被磁场连续条件严格约束，因而没有自由的边条件。对于本文的建模情况，这意味着导体与空气之间的所有边界都需要使用 磁连续性 条件以及该节点下的 电绝缘 特征，来表征导体和空气间磁力线的连续和电力线的绝缘。该条件强制要求导体与空气之间的边界不能有电流流过，无论是传导电流还是位移（电容）电流。

插图突出显示应用了 电接触（洋红色）和 电绝缘（青色）边界条件的面。在建模空间内，这些边界没有自由边。

我们结合使用 理想磁导体（用于强制对称条件）和 磁绝缘 条件模拟建模空间的外部边界，并添加了 接地、电绝缘 和终端子节点，以激励流经母线板组件的电流流动。求解结构问题后，后续的研究步骤在频域内求解电磁问题，从而得到从结构-热模型到电气模型的单向耦合假设。

模型设置的屏幕截图。在磁场连续性边界条件的 电接触 特征子节点设置中，通过 固体力学 接口中的 内部接触 输出计算 接触压力。

可以绘制表面损耗图来显示这种效应，即接触电阻在靠近螺栓处较低，但电流却倾向于流向母线外部边界。

电磁界面损耗图，突出显示了中心附近接触电阻降低，而集肤效应驱动电流远离中心的竞争效应。

流经组件的电流流线图也突出显示了这种集肤效应，以及接触区域的电流线相互挤压。

电流的流线图，突出显示了电流的挤压。

更快、更简单的螺栓连接仿真

固体力学 接口新增的接触边界条件允许用户快速、轻松地模拟接触面之间没有明显相对运动的情况（常见于螺栓连接处）。该条件可与 形成联合体 几何体最终定型方法一起使用，因此可在零件之间的边界上建立连续网格。这样既可以加快收敛速度，又可以方便地添加其他需要连续网格的物理场，例如 磁场和电场 接口。这种组合在螺栓连接的电接触仿真中非常有用，也可用于许多其他应用。

如果您想亲自动手尝试新的边界条件和文中讨论的模型，请点击下面的按钮获取模型。

获取模型

]]>

将时间维度视为空间维度

Fri, 26 Jul 2024 08:19:27 +0000

一些仿真问题能得到非常接近实际情况的解。最近，我在为包含非线性电路问题计算时周期性稳态解时，就发现了一个这样的示例。接下来，让我们来深入探讨这个示例，并看看如何借助COMSOL软件的一些核心功能来高效地实现求解。

仿真场景：非线性变压器

在上一篇使用 COMSOL Multiphysics^® 计算增量电感的博客中，我们探讨了一个由缠绕在非线性磁芯材料上的两个线圈组成的变压器示例。当外加正弦交流电压时，初级线圈和次级线圈会产生感应电流。但是，当电流足够大时，材料的非线性将显著改变增量电感，从而产生非正弦感应电流。我们可以通过建立变压器的全保真模型，或建立考虑了非线性增量电感的等效电路模型来模拟这种行为。非线性使电流随时间呈非正弦周期性变化，我们可以运行瞬态模型多个周期来观察这种逐渐降低到稳定状态的变化。

由缠绕在非线性磁芯上的两个线圈组成的变压器。从有限元模型中提取增量电感，用于等效电路模型中。

运行等效电路模型多个周期后的结果，周期性信号的幅值逐渐接近稳定。

从结果来看，很显然需要模拟多个周期。如果我们只对时间周期稳态解感兴趣，那么大部分生成的数据实际上是不需要的。理论上，在这种情况下我们需要一种能直接获得时间周期解的方法，这正是本文要讨论的内容。

从时间到空间重写等效电路

如果仔细观察该电路模型，我们会发现它只有两个随时间变化的未知数：和 , 即通过初级线圈和次级线圈的电流。现在，让我们从电路的范式来思考问题，考虑两个电流回路中各个元件的压降，用以下方程表示

R_1I_1+\partial L_{11} \dot{I_1}+\partial L_{12} \dot{I_2} = V_{AC}

R_2 I_2+R_{load}I_2 + \partial L_{22} \dot{I_2}+\partial L_{21} \dot{I_1} = 0

其中，所有增量电感都是两个电流的函数：。这组耦合常微分方程可以用多种方法求解。我们仅求解外加电压为，以及方程解的周期为的情况。

很明显可以看出，除了电流的时间导数，这几乎是一组非线性代数方程。但如果用空间导数来代替时间导数呢？让我们看看会发生什么！

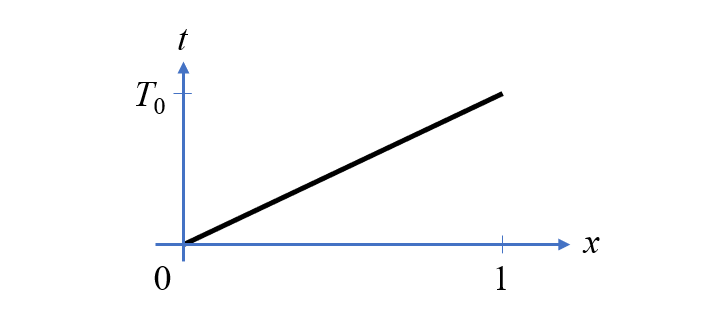
沿一维单元域绘制的时间与位置的函数。

考虑一个一维域，即一条单位长度的直线。定义一个沿长度线性变化的准时间变量。如果在这条直线上定义两个与空间相关的因变量和，并引入网格，那么 COMSOL Multiphysics^® 软件就可以通过微分算子： d(u1,x) 求空间导数。但由于我们将空间维度视为时间维度，因此这实际上是求时间导数。鉴于此，现在可以用 域常微分和微分代数方程 接口构建一个定义在单位长度直线上的场代数方程。该接口的软件界面截图如下图所示，其中定义了两个未知数。使用拉格朗日单元划分这些场，这会自动确保场的连续性，然后，需要给场和源设置合适的单位。为了便于阅读，还可以定义一组变量来描述电路模型中每个元件所产生的压降，如下图所示。

域常微分和微分代数方程 接口设置，包括设置场变量名称、选择形状函数和设置单位。

定义了时间空间的外加电压、电流导数以及电路各元件上的压降的变量。

我们将在 域常微分和微分代数方程 接口的 代数方程 特征使用这些变量，该接口包含两个编辑框，需要输入必须始终等于零的方程。在这个示例中，我们输入两个电流回路的电压降项和源项，也就是上文中列出的方程。最后，在域终端的一个点添加两个逐点约束。此处是通过积分特征，在另一个点上定义的约束 u1-intop1(u1) 和 u2-intop1(u2)，来实现周期性边界条件。

在单位域输入时间空间的代数方程。

通过逐点约束和积分 特征定义周期性边界条件。

当变压器进入非线性状态时，要求解这个稳态问题，需要在域上设置相对较细的网格。因此，在求解这种非线性稳态模型时，求解域上网格的尺寸是需要测试的参数。稳态模拟结果如下图所示，将其与瞬态结果进行比较，结果显示二者非常吻合。事实上，当以更严格的容差求解瞬态模型时，二者之间的差异就越小。但即使是这样一个小模型，高精度的计算都会显著增加瞬态计算的成本，而稳态计算几乎可以瞬间求解。

电路模型计算出的瞬态结果与使用时间周期方法计算的稳态结果的对比。

通过空间 FFT 数据集 特征，我们还能使用空间中一个周期的解提取频率组成。该特征的设置如下图所示，其中突出显示了一维阵列 数据集，该数据集会对计算结果进行周期性扩展，使结果看起来更加平滑。通过绘制适当归一化处理的量，我们可以看到频率组成如何随着外加电压的增加而增加。

空间 FFT 数据集将一维阵列数据集作为输入，周期性的对稳态计算结果进行拓展。

交流电压升高时的频率组成。

结束语

这篇博客，我们介绍了一种特别高效的方法，求解用一组代数方程描述的系统的周期性稳定解。需要注意的是，只要存在平滑的周期性解，这种方法就可以使用任何类型的应用信号，而不仅仅是正弦强制函数。此方法设置非常简单，并且利用了 COMSOL Multiphysics^® 的核心功能，因此适用于任何类型的问题，而不仅是电路问题。对于使用COMSOL 的仿真人员来说，这是一项非常有用的仿真技术。

您可以点击下方按钮，下载相关示例模型：

获取教程模型

]]>

在 COMSOL Multiphysics® 中计算增量电感

Mon, 15 Jul 2024 05:49:12 +0000

在模拟包括线圈、非线性材料、磁体和运动部件的低频电磁系统时，经常需要计算增量电感。当线圈通过随时间变化的电流驱动时，增量电感可用于量化这类电磁系统中产生的场，而且这个量对于建立简化的集总模型尤为有用。接下来，我们将介绍在 COMSOL Multiphysics^® 软件的附加产品 AC/DC 模块中使用增量电感的理论和实践背景。

理论简述

当电路中有一条或多条导线回路时，就会涉及电感的概念，这些导线回路（或线圈）可以由一匝或多匝导线组成。假设其中一个线圈连接源，可将其称为初级线圈；如果其他线圈连接负载，则称为次级线圈。这些负载可以是其他电气设备的任意组合。

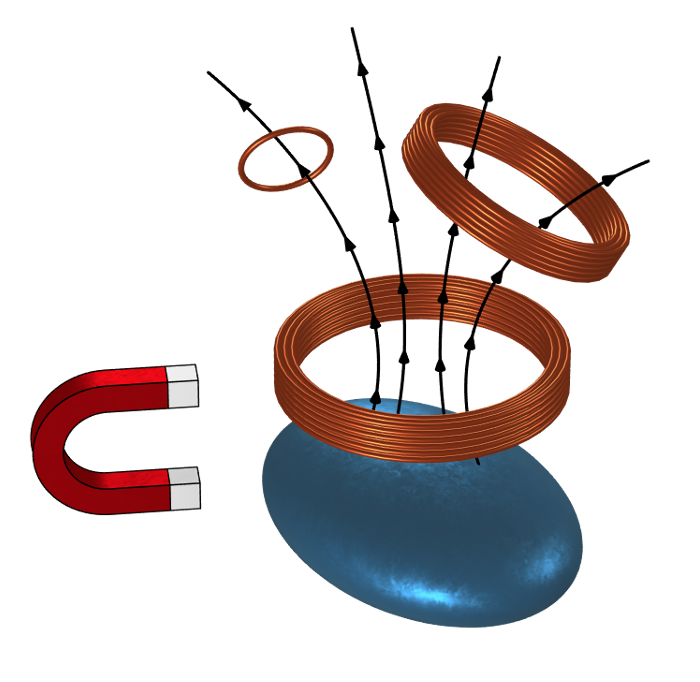
空间中的线圈、非线性磁性材料和磁体。一个线圈中的时变电流将在其他线圈中产生正比于拦截磁通量的磁场，其中偏置的非线性磁性材料将对这些拦截通量产生影响。

在线圈周围的空间中可能存在非线性磁性材料和磁体。非线性磁性材料会受到磁体、流经线圈的电流，或者在二者的共同影响下进入非线性状态。当向初级线圈施加时变电流时，包括初级线圈本身在内的所有线圈都会产生感应电动势（电压）。假设施加的信号频率远低于系统的谐振频率，就可以认为此电动势完全由时变磁场产生。基于这一假设，我们可以使用线圈特征进行计算。

当给定的时变电流流过第个线圈时，其他第个线圈的感应电动势与磁链¹的变化率成正比:

\varepsilon_ j=\frac{d \Phi_{ij}}{d t}

假定是瞬时电流的唯一函数，应用链式法则：

\varepsilon_ j=\frac{d \Phi_{ij}}{d I_i}\frac{d I_i }{d t} = L’_{ij} \dot{I_i}

可以看到，感应电压为关于电流的增量电感和施加电流的变化率的乘积。请注意，如果系统中的所有材料都是线性，不存在磁体，并且忽略导体中的电感损耗，那么上式可以简化为:

\varepsilon_ j=\frac{ \Phi_{ij}}{ I_i}\frac{d I_i }{d t} = L_{ij} \dot{I_i}

式中，是视在电感，只要使用了线圈特征，软件就会默认计算。另一方面，计算增量电感还需要一些额外的步骤。

要理解如何计算增量电感，首先需要了解磁链。在工程类基础教材中，磁链通常被表述为：对激励线圈在表征线圈的导线环表面所产生的磁通量进行积分:

\Phi_{ij} = \int_{S_j} \mathbf{B}_i \cdot dS_j

然而，如上图所示，大多数线圈的横截面积都很大，因此不可能简单地定义一个表面。应用散度定理和，可以通过磁矢势与表征线圈中电流方向的点乘后的体积分来计算：

\Phi_{ij} = \int_{V_j} \mathbf{A}_i \cdot \left(\mathbf{J}_j / | \mathbf{J}_j|}\right)dV_j

使用线圈特征时，软件会自动计算出这一数值，并将其称为线圈级联通量。

这个量可以是许多不同变量的函数，尽管我们之前假设它只是瞬时电流的函数。现在，让我们来看看如何求导数来提取增量电感。

计算增量电感

要计算增量电感，需要评估所有线圈中的线圈级联通量关于初级线圈施加电流的导数，这可以通过 灵敏度 接口实现。我们在使用 COMSOL Multiphysics^® 计算设计灵敏度的博客中介绍过这个接口，现在简要回顾一下。首先，要定义 全局目标 特征，其中需要输入线圈级联通量的表达式。还需要定义至少一个 全局控制变量 用于计算目标函数微分。然后，输入一个与流经初级线圈的直流电流相乘的变量名。通过这种设置，可以将 灵敏度 研究步骤与施加电流的 辅助扫描 相结合，计算施加电流范围内的增量电感。

在灵敏度 接口中定义目标函数。

在灵敏度 接口中定义控制变量。

使用线圈 特征中的控制变量设置关于电流的微分。

在一定范围内扫描电流，同时计算灵敏度。

求解后，创建一个引用 计算组的插值 函数，以便在模型的其他地方使用增量电感的计算结果。

了解这些基本理论和工作流程后，现在让我们来看几个示例。

非线性电感器

首先，我们模拟了一个由合金铁氧体制成的磁芯，合金铁氧体是一种损耗极低的非线性磁性材料。磁芯从内部和外部包裹着一个线圈。我们采用了二维轴对称模型，其中线圈由 80 匝直径为 1 mm 的导线组成，工作频率为 50 Hz，因此这些导线的趋肤效应可以忽略不计，可以通过直流电阻准确预测线圈的交流电阻。在这个示例中，我们可以使用 多匝线圈域 特征在时域中求解，以获得在施加正弦电压作用下通过电感器的非正弦电流。

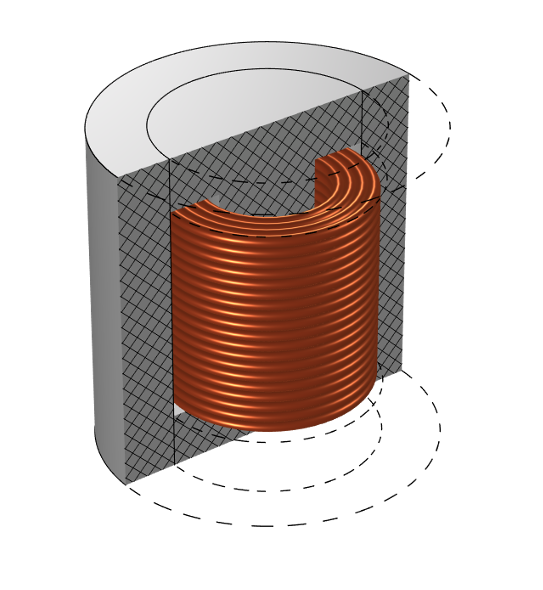
BH 非线性磁芯和环绕线圈组成的电感器。

首先，求解该模型在一定直流电流范围内的电感值，得到如下图所示的增量电感，以及用于对比的视在电感。

由非线性磁芯材料制成的电感器在一定直流电流范围内的增量电感和视在电感。

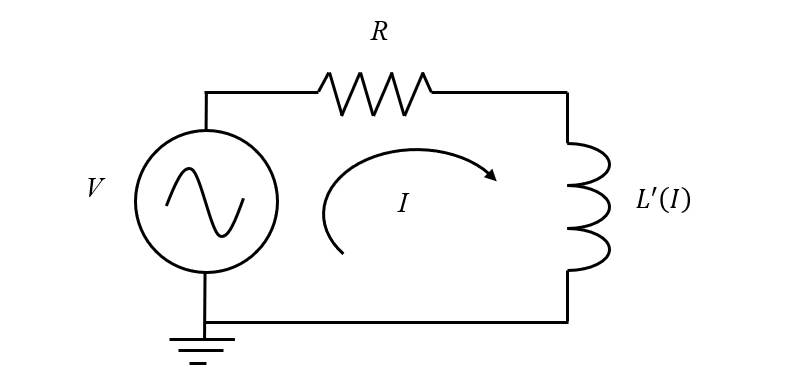
非线性电感器的等效电路模型，其中增量电感是电流的函数。

获得增量电感后，我们就可以在电路模型中使用它来快速预测瞬态行为。除了默认的 接地节点 特征外，建立电路模型只需要三个特征：

电阻特征
电感器 特征
电压源 特征

使用一个电阻特征，阻值设置为使用线圈特征计算出的电阻值。在此基础上，添加一个 电感器特征，其非线性电感由存储了之前计算的增量电感的插值表定义。因为非线性特性与电流符号无关，所以可以将该非线性电感设为电流绝对值的函数。最后，将 电压源 特征串联接入。这三个特征共同创建了一个可预测响应的集总模型，将其计算结果与有限元模型的结果进行对比。请注意，在前几个周期内，结果表明仅仅只是开始接近此非线性系统的周期性稳态响应。

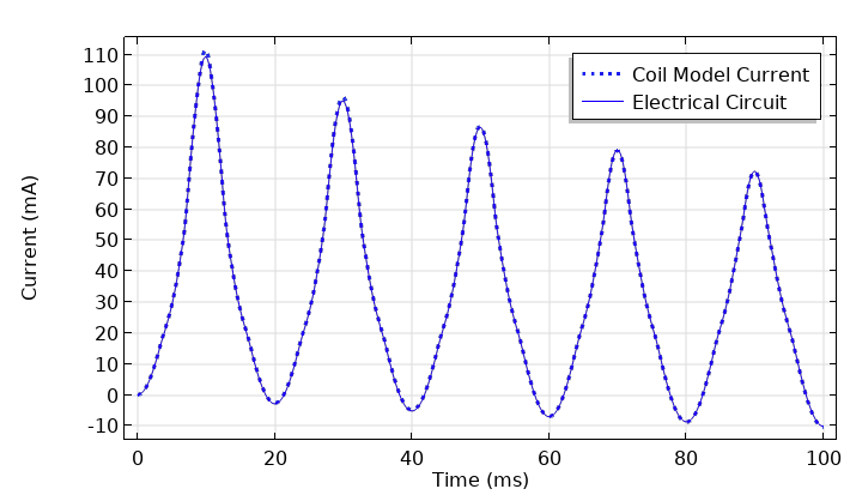
施加交流电压源时流经电感器的电流。电路模型和磁场模型的计算结果一致。

我们还可以通过傅里叶变换将这些时域数据转换到频域，以更清晰地识别由材料非线性引入的高次谐波。由于电路模型可以快速求解，我们还可以快速检查各种工作条件。不出所料，当设备进入非线性区时，会出现更多的高频分量。

电流的频谱图及其随峰值电压的变化。

含偏置磁铁的非线性电感器

为了便于说明，我们现在将上述示例进行修改，在磁芯旁边放置一块磁铁，磁铁将对线圈级联通量做出贡献，并使非线性材料发生偏置。现在，增量电感取决于施加电流的大小和符号。值得注意的是，正弦电感包含了磁铁本身对并联磁通量的贡献，但这种不随时间变化的磁通量不会对反向感应电压产生影响。磁铁只会改变系统内任一非线性材料的 B-H 关系。也就是说，磁铁不会影响仅由线性材料制成的电感器的响应。不过，必须牢记的是，磁铁始终会在正弦电感中引入偏置。因此，只要模型中存在磁铁，即使所有材料都是线性的，最好也使用增量电感。

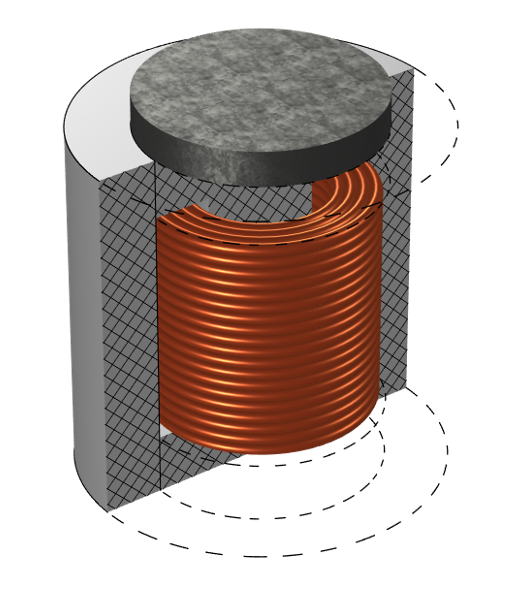
放置在 B-H 非线性磁芯顶部的磁铁会使响应偏置。

在偏置电感器中，增量电感与直流电流的符号不对称。

增量电感可再一次用于电路模型，我们再次看到，除启动期间外，二者的计算结果非常吻合。启动期间的这种不一致，凸显了用于计算空间变化场及磁芯饱和空间演变的模型与集总模型之间的差异。

空间有限元模型与包含偏置增量电感的集总电路模型的计算结果基本一致。

变压器的非线性响应

接下来，让我们来看一个由围绕合金铁氧体磁芯上的两个相同线圈组成的变压器示例。由于和，对称性不仅可以用来减小模型大小，还可以减少计算量。一般情况下，增量电感可以是（初级电流）和（次级电流）的函数，但对于这种对称结构，，我们只需要计算增量电感和；保持的情况下，在的范围内计算，无需对两个变量进行扫描。

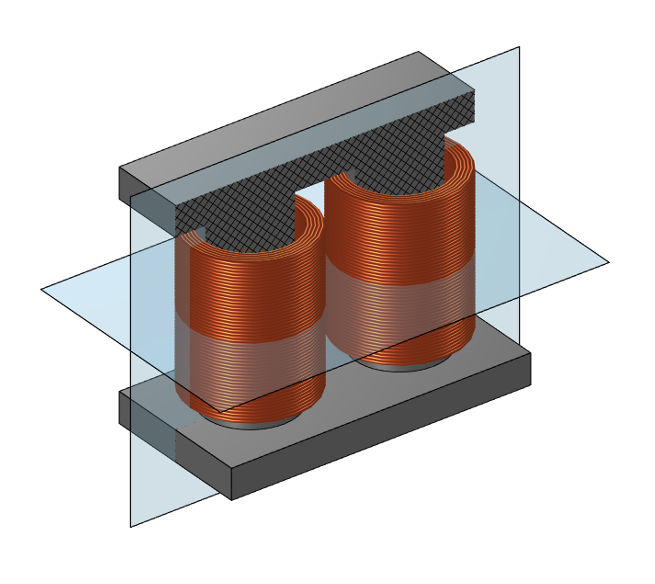
由围绕在对称磁芯上的两个相同线圈组成的变压器，图中可以看到两个对称平面。

计算出这两个增量电感后，就可以使用一组函数来定义互感矩阵的所有四个项。这些项可以在同一变压器的电路模型中使用。由于存在非线性，两个线圈之间的耦合通过 电流控制的电压源 特征模拟，如下图所示。

含非线性磁芯的变压器等效电路。

使用完整的三维模型求解该变压器的响应需要大量的计算成本，而使用电路模型求解则非常快速。尽管在所有可能的运行工况下计算增量电感矩阵非常重要，但我们最终得到的结果还是非常吻合。为了提高计算效率，可以通过批处理或集群扫描的并行方式一次性计算所有工况，以充分利用所有可用的计算资源。

施加在初级线圈上的正弦交流电压会在初级线圈和次级线圈上产生非线性电流。使用完整的三维模型和电路模型求解的初级线圈上的电压和次级线圈上的电流的对比。

螺线管线圈的动态响应

现在，让我们来看一个由铁质外壳内的线圈和铁质柱塞组成的螺线管。柱塞的安装方式使其只能沿其轴线移动。假设铁的磁导率在预期磁场范围内保持不变，并忽略材料的非线性。同时假设外壳和柱塞是绝缘材料，能将绕轴线的所有感应电流降至最低，因此可以将铁芯视为无损耗材料。

由铁制外壳内的线圈和由弹簧固定的铁柱塞组成的螺线管线圈。

弹簧将柱塞固定在壳外的位置以保持平衡。当向线圈施加电压时，电流开始流动，并推动柱塞向中心移动。在这种情况下，不存在材料非线性，因此级联通量与瞬态电流呈线性关系，但与柱塞的 z 向位置呈非线性变化：

\Phi(I,u) =I L(u)

因此，根据链式法则，反向感应电压为：

\varepsilon=\frac{d \Phi }{d t} = \frac{\partial \left(IL(u)\right)}{\partial I}\frac{\partial I }{\partial t} + \frac{\partial \left(IL(u)\right)}{\partial u}\frac{\partial u }{\partial t}=L(u) \dot{I} + I \frac{\partial L(u) }{\partial u} \dot{u}

式中第一项考虑到了视在电感随柱塞位置变化这一事实。当柱塞在非零磁场中以速度运动时，第二项引入了一个额外的反向感应电压。

考虑到级联通量与施加的直流电流（）呈线性关系，第一个方程对位置进行微分得到：

\frac{\partial L (u)}{ \partial u} =\frac{1}{I_{DC}}\frac{\partial \Phi(I_{DC},u)}{ \partial u}

因此，为了计算关于位置的导数，结合使用 灵敏度 接口与 动网格 接口，在保持直流电流不变的情况下，计算级联通量关于 z 位置无限小变化的偏导数：

\frac{\partial \Phi(I_{DC},u)}{ \partial u} =\frac{\partial \Phi (I_{DC},u+\delta) }{ \partial \delta}

我们通过 动网格 接口引入了 z 向位置的有限和无限小变化，然后对无限小位移（）求偏导，并沿柱塞行程的一系列不同位置（）进行扫描。通过偏导结果，现在可以建立一个简单的机电集总模型，将电路模型与柱塞运动方程结合起来。

机电集总模型由一个电路模型和一个集总机械模型组成，其中集总机械模型由柱塞运动时的力、与位置相关的视在电感和反向感应电压耦合。

由集总系统的示意图可以看到，电气系统通过力与机械系统耦合。要理解力的表达式是如何得出的，让我们先来看看系统中随电流和柱塞位置变化的总磁能的表达式：

W_m(I, u) =\frac{1}{2}L(u)I^2

柱塞上的总力可以通过虚功方法求得，对于线性磁性材料，轴向力可以通过总磁能关于无限小位移的偏导数求得：

F_z(I,u) = \frac{\partial W_m(I, u)}{\partial u} =\frac{I^2}{2}\frac{\partial L(u+\delta)}{\partial \delta}

也就是说，力是通过线圈的电流和电感关于位置的偏导数的函数，这一点我们已经计算过了。因此，在模拟螺线管的同时，我们还要求解柱塞位置的常微分方程：

F_z(u) = m_0 \ddot{u}+k_0\left(u-u_0\right)

式中，是柱塞的平衡位置。这个方程可以通过 全局常微分方程和微分代数方程 接口或可添加到任何物理场接口的 全局方程 特征来求解。因此，该方程可以与磁场接口耦合来求解运动，还可以与电路接口耦合进行求解。

我们将使柱塞沿轴线自由振荡，并根据一组输入的结果来研究其产生的一些动态过程，目的是说明集总模型与用于计算集总参数的空间模型的计算结果非常吻合。

螺线管磁场的精确模型与集总模型的计算结果对比。

尝试建立集总模型

这篇文章，我们通过 4 个示例重点展示了 COMSOL Multiphysics^® 软件不仅可以提取增量电感，还可以计算线圈级联通量关于其他输入变量的导数。由此得到的量可用于构建简化的集总模型，从而准确预测系统的性能。

想尝试自己动手计算增量电感并建立这类集总模型吗？请点击按钮，进入 COMSOL 案例库，下载文中的示例模型：

下载模型

参考文献

1. D. Cheng, “Field and Wave Electromagnetics”, 2nd ed., Addison-Wesley, 1991

]]>

电力输电线的电场和磁场仿真

Wed, 15 May 2024 01:39:52 +0000

为确保电力输电线周围人员和环境的安全，工程师必须对电力线产生的电场和磁场进行监控。通过多物理场仿真，工程师能够预测电力线产生的场如何从电力线中扩散，以及如何影响其辐射至地面的强度。这篇博客，我们将使用两个示例模型来说明如何使用 COMSOL Multiphysics^® 软件分析由电力线产生的电磁场。

无形的能量场

我们日常使用的大部分电力都来自高压到低压电力输电线，这些电力线会产生电场和磁场（EMF）。电力线可以传导强低频电流，产生随着距离的增加而迅速减弱的非电离电磁场。尽管如此，为了确保电力线对周围人和环境的影响保持在安全范围内，对其产生的电磁场的暴露和输出进行监控仍然非常重要。

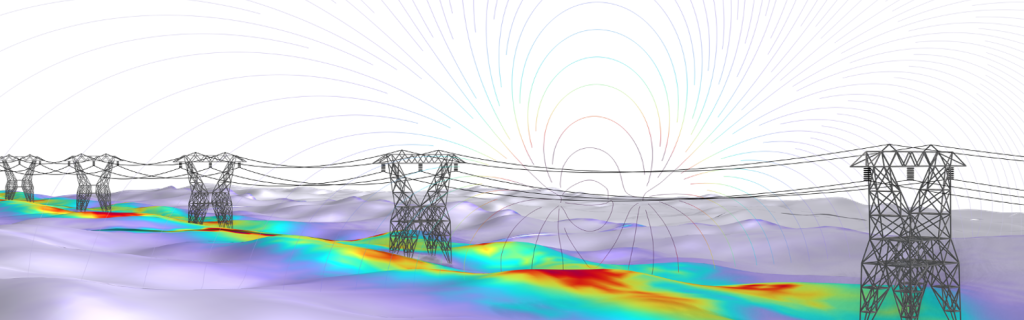
图 1 远距离电力输电线模型。

接下来，我们将通过两个示例模型来探讨如何利用建模和仿真分析电力输电线产生的电场和磁场。这些示例将重点关注场强及其与电力线和铁塔的分布关系。

如何建立两种电力线模型

您可以在COMSOL 案例库中找到电力线的电场和电力线的磁场教程模型，模型中用两个塔架传输高压三相交流电。铁塔的相线上方装有两条屏蔽线，用于防止雷击造成损坏。在如此高电压的电力线路中，相线通常由几条较小的导线捆束而成。为了简化模型，每条相线只使用一根半径为 10 厘米的导线来模拟一束导线。在每个模型中，都将地平面设置为随机扰动面，以模拟地球的不规则性。

图 2 左图：电力输电线的照片，由 David Levêque 拍摄，图片来自 Unsplash 。右图：输电塔的几何形状。可以看到顶部的两条屏蔽线，以及由绝缘子固定的三条相线。

我们已经介绍了这两个模型的基本几何结构，接下来，让我们来看看它们各自的仿真结果。(请注意，如需获取建立这些模型的分步说明及其 MPH 文件，可以点击文末链接，至COMSOL 案例库中下载。)

电场模型

在电场模型中，用户可以设置每条相线的电压幅值和相位。(在图 3 所示的场景中，电压设置为 400 kV，相间隔为 120^º 。）此外，由于使用了边界元法，以及所有的边和表面均为固定电势，因此模型只需要在这些实体上建立网格。相比之下，采用有限元法时，模型需要在整个空气域内创建体网格，这将大大增加自由度的数量，并延长模型求解所需的时间。

仿真结果显示了线路在地表产生的电场模，以及空气中指示局部电场方向的流线。在电线附近，电场形成了一个分支图形。电场在靠近电线的地方最强，随着距离的增加而减弱。了解电场的传播距离可以帮助工程师确定建筑物与电力线的距离，从而最大限度地减少暴露，并确保电场强度符合相关规定。

图 3 电力输电线的电场模（表面图）和电场（流线图）。

磁场模型

在磁场模型中，每条相线都能传导 1000 A 的电流。与电场模型一样，磁场模型中的相也间隔 120^º 。模型中的所有外部边界都采用了默认的磁绝缘边界条件。

与电场模型一样，磁场模型的结果也显示了线路在地面上产生的磁场模和指示磁场方向的流线，这些流线形成闭合回路。该模型中的磁场也是在靠近电线的地方最强，随着距离的增加而减弱。

图 4 电力输电线的磁场模（表面图）和磁场（流线图）。

下一步

在这篇博客中，我们讨论了使用 COMSOL Multiphysics^® 建立的两个用于检查电力输电线产生的电场和磁场分布的案例模型。这些模型对于测量电磁场的范围和行为非常重要，可以帮助我们进一步了解电磁场如何与周围环境相互作用。

想尝试自己模拟电力输电线中的电磁场吗？您可以点击下方案例模型链接，获取文中讨论的模型及其详细分步说明:

扩展阅读

阅读COMSOL 博客，了解更多有关仿真在电磁场暴露研究中的作用的信息:

]]>

如何在用户定义的材料库中添加材料信息

Fri, 10 May 2024 03:13:23 +0000

你知道吗？在 COMSOL Multiphysics^® 软件中创建用户定义的材料库，并向库中添加自定义材料时，可以为这些材料添加相关信息，包括材料属性的引用以及相、取向、材料编号和其他常规信息。在这篇博客中，我们将向您介绍如何添加材料信息。

在材料属性中添加引用和其他信息

COMSOL 材料库产品中的所有材料属性都包含引用信息，它描述了材料属性数据的来源，并附有其他说明，例如数据的计算方法或与温度有关的数据插值的限制。在COMSOL 产品库的附加模块或多或少也内置了包含材料引用信息的材料库，如电池材料库。要查看这些材料属性的引用信息，请打开材料浏览器窗口（例如单击材料功能区上的 浏览材料 按钮）。在选择含属性引用信息的材料时，单击属性就可以查看其引用信息。

材料库产品中 DocolS355 钢材料恒压热容的属性引用信息,方向/变化 栏显示了钢的成分。

添加自定义的材料属性引用信息

如果要为添加到用户自定义材料库的材料添加自定义的材料属性引用信息，可以通过以下步骤完成：

添加新材料，并在包含常用材料属性的属性组子节点（如基本）中定义要使用的输出属性和模型输入。
定义材料属性的表达式，可以是数值，也可以是对插值函数的调用，例如作为子节点添加。
在 输出属性 部分，表格中列出了所添加的材料属性及其变量名、表达式和单位。最右边的信息栏初始为空，但最终会包含符号，表示有引用信息或其他信息可供查阅。
点击要添加信息的属性所在的行，激活表格下方的 编辑/显示属性信息 按钮。(该按钮与信息栏中显示的符号 ) 相同。）单击该按钮可打开 编辑/显示属性信息 对话框，在信息栏中输入任意引用或其他信息。
完成后，单击确定保存属性信息并关闭对话框。符号就会出现在该属性的信息栏中。您可以再次单击 编辑/显示属性信息 按钮查看或编辑信息。
如果将材料保存到用户定义的材料库中，就可以如上所述在材料浏览器窗口中访问和查看这些属性信息。

单击属性可激活表格下方的 编辑/显示属性信息按钮，

编辑/显示属性信息 对话框提供了材料密度的一些引用信息。

添加相、取向和其他材料信息

对于要添加到用户定义的材料库中的自定义材料，可以添加如相或取向等可选的材料信息。这些设置可以在材料节点的设置窗口的 材料库设置 部分找到。要激活该部分（仅适用于在全局定义节点下添加的材料），请打开 显示更多选项 对话框，然后选择常规节点下的 材料库设置 复选框并单击确定。

在 材料库设置 部分，可以从相菜单中定义一种相— 固态、液态、气态或 自定义，并在 方向/变化 栏中添加某种材料取向或变化。当使用组节点建立用户定义的材料库时，用户能够在材料库中创建一个结构，其中包含文件夹和具有不同相、取向或其他变化的材料。创建具有这些属性的用户自定义材料库，需要将材料库保存为 MPH 文件，然后将该文件导入材料浏览器窗口。在组和材料节点中的标签栏，需要使用相同的材料名称，然后在括号中标注相，（如[固体]），或同时包含相和某些方向取向和变化，（如 [固体,nbc]）。然后，这些标签将被转换为材料浏览器窗口中相和 方向/变化 菜单中的列表条目。

在 材料信息 下，您可以添加各种类型的材料信息，包括分类和编号标准或特定材料的其他名称：

AFNOR: 法国标准化协会，总部设在巴黎的标准组织，也是国际标准化组织（ISO）的法国成员机构
AISIM: 美国钢铁协会（AISI）材料名称
AMS: 美国汽车工程师学会（SAE）航空航天材料标准（AMS）
ASTM: ASTM 国际，一个国际标准组织
自定义 （默认）：添加任何自定义材料信息类型
DIN: 德国工业标准（DIN），一个德国标准
ISO/EN/DIN: ISO 通用的编号;欧洲标准，也称为欧标（EN）;和 DIN
JIS: 日本工业标准（JIS），一种日本标准
SAE:美国汽车工程师学会(SAE)的材料名称
UNS: 统一编号系统，一种在北美被广泛接受的合金命名系统
WNr: 德国材料编号系统

要在表格中添加包含材料信息的新行，请单击下方的添加按钮 ()。然后单击 编辑材料信息 按钮 ( ) 打开 编辑材料信息 对话框并添加信息。从类型列表中选择一种材料信息类型。如果选择 自定义 选项，还需填写信息类型的标题栏。对于所有条目，在信息栏中添加所需的文本。定义好材料数据编号或名称后，可以使用材料浏览器左上角的搜索框在所有材料库中搜索匹配的材料。输入搜索词，例如 UNS 编号为 G10060，然后单击搜索。搜索框下方的材料库树将只显示与该搜索词匹配的材料。

下一步

这篇博客，我们介绍了如何将材料属性信息和其他信息添加到用户的模型中，并存储在用户定义的材料库中。这些库可用于存储材料，供个人使用或在组织内部共享使用。

要了解在软件中使用材料的更多信息，请查看以下 COMSOL 网站资源：

]]>

电流模型中的色散仿真

Wed, 20 Dec 2023 05:50:48 +0000

随着 6.2 版本的发布，COMSOL Multiphysics^® 软件模拟电色散的功能现在已经扩展到支持时域和频域仿真的电流接口。这个功能对于包括绝缘体和活体组织在内的各类材料的精确仿真尤为重要。这篇博客，我们将简单复习一下什么是色散，然后介绍如何将其纳入 COMSOL 模型，并讨论为什么这个功能很重要。

背景知识

在模拟施加到活体组织的快速脉冲电流时，例如在心脏消融、电穿孔或神经刺激等应用中，需要考虑组织以及电绝缘体的色散性。

所有材料都有电色散性，也就是说相对介电常数随激励频率的变化而变化。介电常数是一种衡量材料在电场作用下的响应或极化程度的指标。由于材料及其结构中的原子和分子不同，响应的大小随频率而变化。这也是衡量当材料暴露在时变信号下时有多少电能可转化为热能或损耗的标准。这些损耗由原子和分子在时变场中振荡时发生相对运动而产生。在频域中工作时，相对介电常数用复数表示：，其中，实部和虚部通过 Kramers–Kronig 关系确定。下图显示了两条色散曲线，分别代表绝缘材料和活体组织。第一幅图中的曲线相对简单，在较宽的频带内的特性几乎一致，因此并不总是有必要考虑色散问题。另一幅图中，总有一个频段内的特性会发生显著变化，故有必要考虑色散。

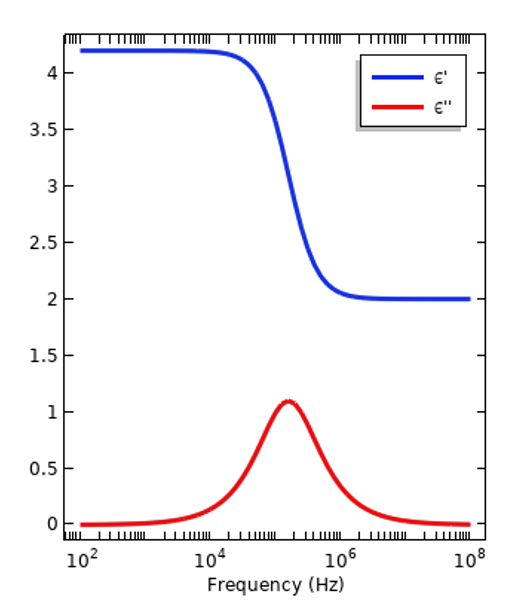
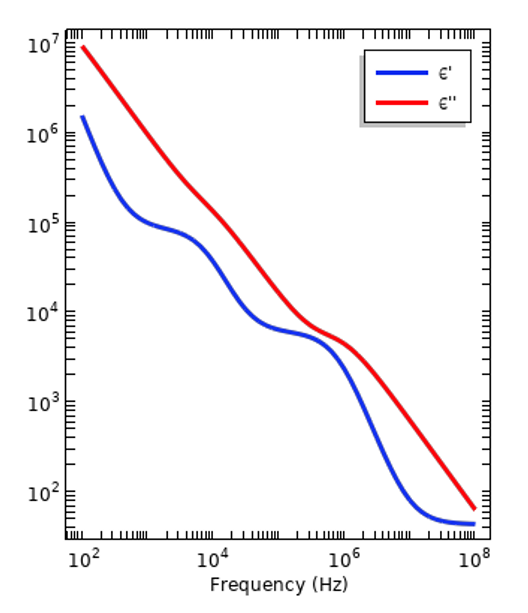
绝缘体（左）和活体组织（右）的代表性色散曲线。图中绘出了相对介电常数的实部和虚部分量的大小。

除了与频率相关的损耗之外，静态电场中也存在电损耗，这些损耗可以用直流电导率来量化。所有材料都有一定的直流电导率，但可能非常非常小。这是一种与色散损耗不同的损耗机制。用总电导率来表示所有的材料损耗（无论其机制如何）比较方便: ,下图是同样两种材料的总电导率。不过，需要注意的是，与频率相关的电导率也可以不含直流分量，例如，，其中单独绘制。

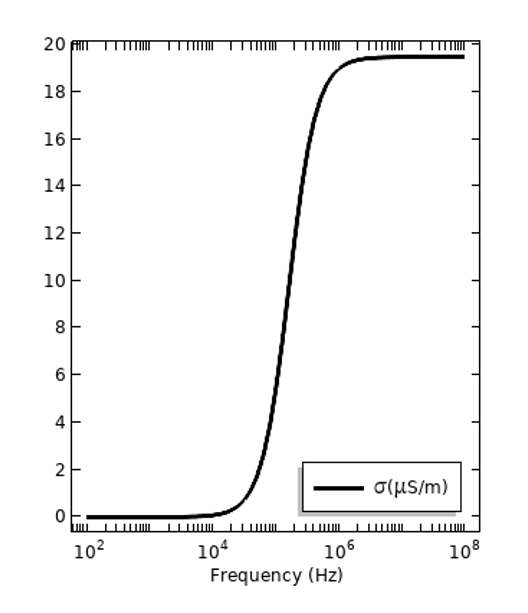
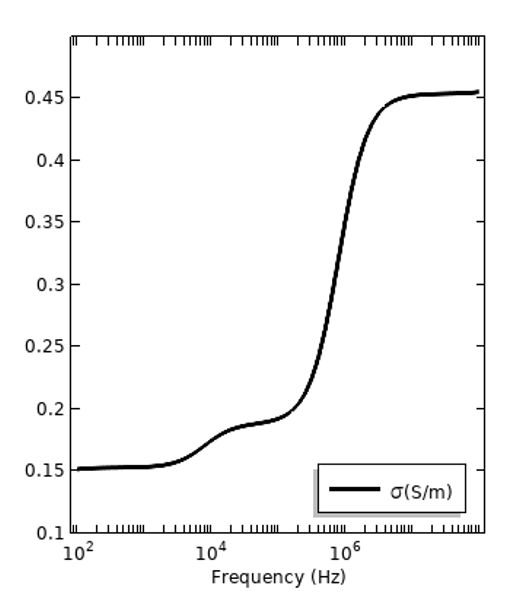
绝缘体（左）和活体组织（右）的总电导率损耗，其中包含直流电导率对色散损耗的贡献。

虽然材料特性是通过实验确定的，但我们并不想直接使用实验数据，因为这些数据会有一些不确定性，并且不满足 Kramers–Kronig 关系，从而需要非因果建模。相反，我们会将数据拟合成一个已经满足 Kramers–Kronig 关系的函数，并使用该拟合函数的系数来描述材料行为。目前，软件支持多极德拜 模型，该模型将任意数量的极点作为输入，其中每个极点都有一个弛豫时间和相对介电常数，由此定义的复值介电常数为：

\epsilon_r = \epsilon_\infty + \displaystyle {\sum_{m=1}^N}\frac{\Delta \epsilon_{rm}}{1+i\omega \tau_m}

其中，基于低频限制或高频限制。此外，由于温度的变化，弛豫时间可以选择使用 Vogel-Fulcher、Arrhenius、Williams-Landel-Ferry 或 Tool-Narayanaswamy-Moyniha 转换函数中的任何一种，甚至是用户自定义的转换函数。

如果您有介电常数实部和虚部的实验数据，并希望拟合出德拜模型，则可以使用 COMSOL^® 6.2 版本中的部分分式拟合 功能来实现。有关该功能的使用指南，请参阅 COMSOL 学习中心的文章：根据实验数据拟合德拜色散模型。

使用电流接口

在电流模型中加入色散只需要几个步骤。首先，必须添加电流守恒 域特征并将其应用在相关域。在该特征中，材料类型 必须设置为固体。在假设流体不变形的情况下，这个特征也可用于流体仿真。

电流守恒 特征，可选择 色散介电模型。

将介电模型 选项更改为色散后，将出现一个附加子功能。在该功能中，可以输入多极德拜模型的分支以及限制行为，如下图所示。除了输入极点或分支外，还可以通过恒定损耗角正切 模型指定弛豫数据，该模型将损耗角正切、中心频率和带宽作为输入。根据这些输入，软件会自动确定极点数、弛豫时间和相对介电常数。也可以使用更简单的德拜模型，该模型只有一个极点。通过热效应设置可以选择启用导致弛豫时间转换的热效应。

输入多极德拜模型的分支和指定限制行为的 色散子特征。

查看结果

我们可以研究色散如何影响一个简单系统的响应，例如在频域中工作的平行板电容器案例模型所示，也可以尝试将两种不同的材料夹在其中。由下图我们可以看到阻抗的实部和虚部是如何随频率变化的。

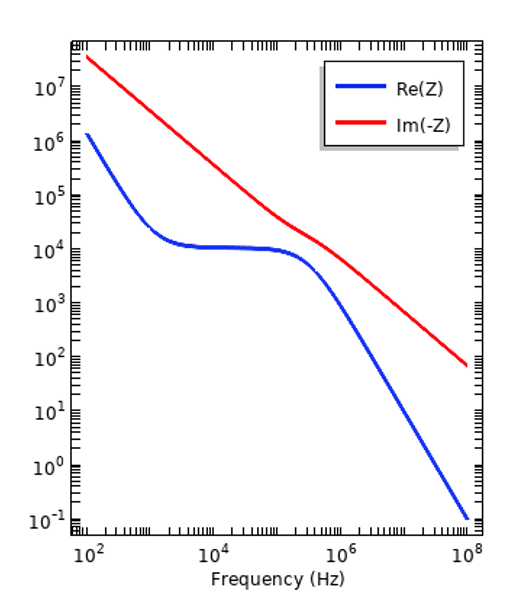
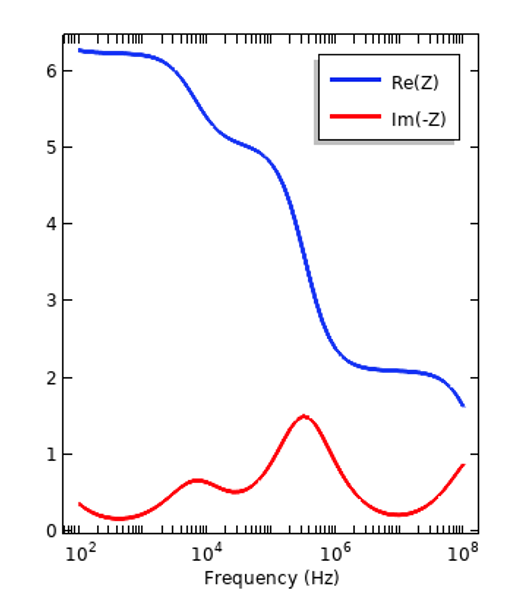
内含绝缘体（左）和活体组织（右）样本的平行板电容器的阻抗。请注意，绘制的是阻抗的负虚部分量。

我们还可以使用相同的模型来查看同一系统中的时域激励结果。我们只研究样本组织材料，因为其响应随频率的变化更为显著。色散材料的设置是相同的，但建议您复习一下这篇博客：激励这种系统的各种方法。我们首先用在 10ns 内从 0 A递增到 1A 的平滑外加电流来激励系统，然后通过绘制终端感应电压图计算 100µs 内的响应（见下图）。结果随时间变化，并以对数标尺绘图。

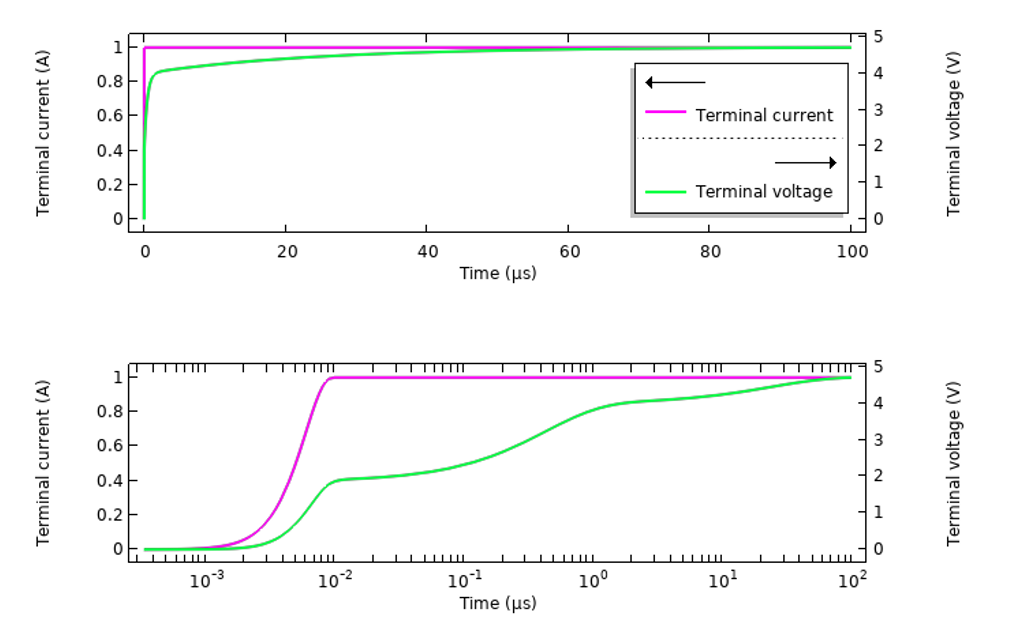
活体组织样本材料对外加电流的瞬时响应。

将这些结果与通过沿传输线传输的类似平滑递增电压信号激励的模型进行比较非常有意思。下图显示了测量的电流和电压的响应。请注意，这里绘制的电压信号是入射的平滑递增电压信号与来自结构和材料的反射信号之和。由于材料的色散作用，总信号表现出时变特性。

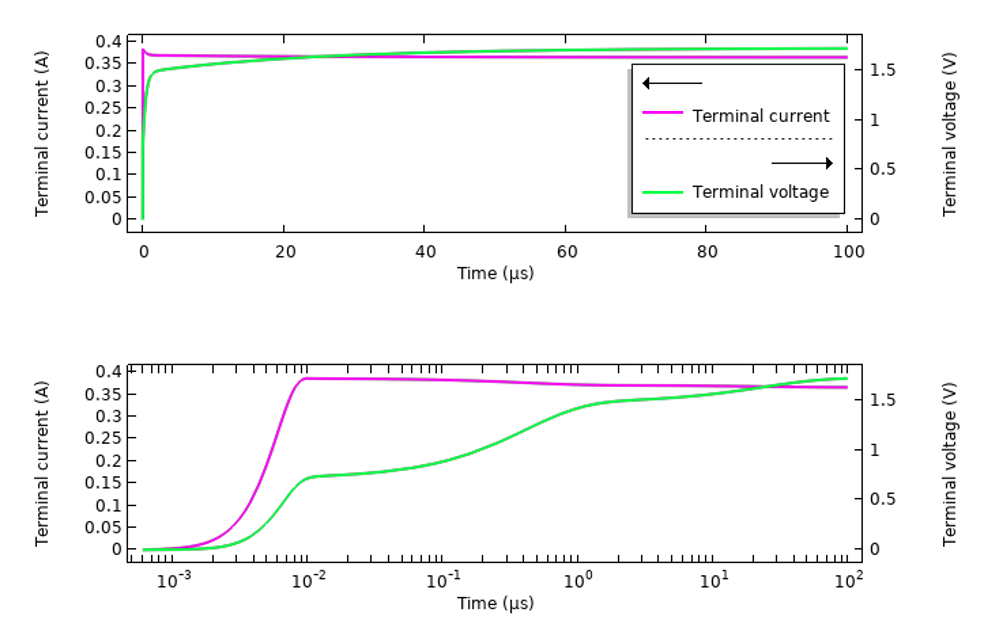
由传输线激励的活体组织样本材料在递增电压信号下的瞬态响应。

结束语

现在，我们可以在电流接口中建立电色散模型，而且设置非常简单。这种材料模型可以更准确地反映真实的电响应，以及频域和时域模型中的损耗。这个功能对许多材料的仿真都非常有用。

请注意，通过静电接口也可以模拟电色散，而且从 6.0 版本开始就可以实现，该接口主要用于有损压电材料的建模与仿真。此外，如果要模拟更高的频率，RF 模块和波光学模块中还包括其他色散模型。

]]>

模拟射频加热的 5 种方法

Thu, 04 May 2023 08:52:37 +0000

COMSOL^® 多物理场软件非常适合用于射频（RF）加热仿真，在这个过程中，需要同时求解电磁场和温度随时间的分布。大家可能会认为，凡是涉及 RF 加热的问题，都需要使用 RF 模块来求解，但在大多数情况下，我们也可以使用 RF 模块或者 AC/DC 模块求解。对于一些典型问题，我们还以使用多种不同的物理场接口求解。接下来，让我们了解更多内容!

简介
通过电磁波接口求解
通过电流接口求解
通过磁场和电场接口求解
其他2种方法
结束语

简介

在开始电磁仿真时，使用 COMSOL Multiphysics^® 中的哪个接口?这个问题有时会引起很大的争议。在博客文章《在 COMSOL 中可以使用哪个模块进行电磁模拟？》中，我们对此做了一些较深入地介绍。然而，有时不同接口适用的频率范围存在明显的重叠，因此使用不同的建模方法可能会产生相同的结果。知道这一点很重要，因为不同的方法有不同的优势。例如，一些方法具有较低的计算成本，而计算成本较高的方法可以提供更多的结果。

需要强调的是，这些重叠的频率范围可能非常具体，我们应该仔细地相互验证。为了证明这一点，这篇博客，我们将讨论一个可以使用不同方法求解的示例。下图为我们将要模拟的系统。

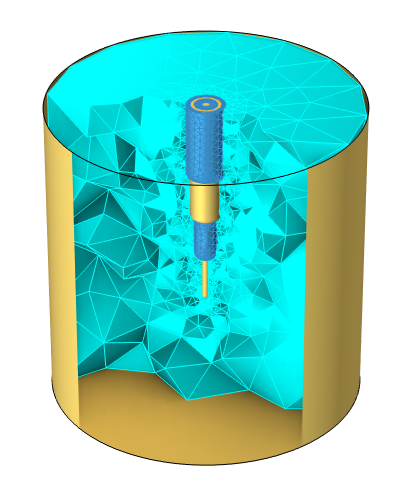
模拟系统：一个同轴探头插入一个充满了有损耗的介电材料样品的金属腔中。

如上图所示，RF 源通过同轴电缆与插入金属圆柱形腔体（高 2 cm，直径 2 cm）中的简单探头相连，该腔体内充满了我们想要加热的有损材料。探头是同轴电缆的延伸，绝缘层和导体暴露在腔体外并且做了光滑处理。我们将考虑的频率范围是 100 kHz–1 GHz。

空腔内的材料是有损耗的介电材料，在所有要求解的频率范围内，相对介电常数为 50，电导率为 30 mS/m。虽然没有一种材料可以在所有频率下都具有恒定的特性，但我们可以假设材料在某些范围内几乎具有恒定的特性。腔壁和同轴电缆的金属电导率为 6e7 S/m，与铜的电导率相同。同轴电缆内部和周围绝缘体的相对介电常数为 1.75，电导率为 1e-12 S/m 。内导体半径为 0.25 mm，外导体半径为 0.75 mm，形成一根具有 50 欧姆阻抗的低损耗同轴传输线。

使用电磁波物理场接口求解

我们将从最高频率 1 GHz 开始建模。因为该频率接近于腔体谐振频率，所以需要使用 RF 模块的电磁波，频域 物理场接口建模。关于特征频率，我们可以通过对这个有损耗的电介质填充的腔体进行特征频率分析，严格地得出这个结论。还有一个必须更加严谨地考虑的问题是：我们使用该接口可以求解多低的频率，以及应该使用哪些边界条件？

关于边界条件，我们知道金属的集肤深度在大部分频率范围内都非常小，因此应该先建立阻抗边界条件，而不是模拟金属域内部的电磁场。最终，我们希望在最低频率范围内更仔细地检查该条件是否适用，因为在 100kHz 时集肤深度与同轴电缆的厚度差不多。通过表征无损耗的电连接的 完美电导体 边界条件将同轴电缆的外导体与腔壁进行电连接。

经常会有人认为空腔壁和外导体是接地的，但是正如我们在博客文章《模拟波状电磁场中的电压和接地》中所讨论的那样，我们应该使用更严谨和准确的术语，简单来说，就是不应该将导电材料看作是接地的，而是低阻抗的导电表面。

对于激励边界条件，我们通过同轴电缆 类型的集总端口 边界条件，将源类型设置为功率，来模拟同轴传输线和源之间的连接。该条件被应用在内导体和外导体之间的环形边界上，也可以使用这个条件模拟任何其他类型的横向电磁 (TEM) 传输线，详细可以参考我们学习中心的文章《模拟 TEM 和准 TEM 传输线》。

应用集总端口 边界条件模拟延伸至无穷远的无损传输线的连接，向集总端口 添加激励意味着无穷远处有一个源向线路发送信号并进入模拟域。该信号的一部分在域和阻抗边界条件内以热量的形式耗散，另一部分被反射回来。我们最终想要通过模型计算的是耗散的热量。了解有多少输入信号被反射回来也很有用，它可以由 S 参数量化。

介电材料样品在 100MHz 时的损耗，箭头表示电场。

我们将在整个感兴趣的频率范围（100 kHz–1 GHz）内求解该模型，并计算样品介电材料的 S 参数和总温升。但是，在更低的频率下，将会出现一个我们无法再解析出的点。这是可以预测到的，因为电场开始接近静态极限。因此，全波公式不再适用，我们必须寻找其他方法。

通过电流接口求解

在非常低的频率（远低于 100 kHz）下，这就变成了一个可以用电流物理场接口求解的问题，它求解的是（标量）电势而不是（矢量）电场。让我们研究一下在仍然能获得相似结果的情况下，使用这个接口可以求解的最高频率是多少。

使用电流物理场接口时，边界条件是不同的。首先，当接近静态极限时，需要设置一个接地边界条件，并且需要对此条件进行清晰的定义：沿着该边界上两点之间的任何路径的电场积分为零。有关直流情况的详细讨论，请参阅我们的博客文章《电压和接地存在吗?》虽然我们知道这个接地边界条件在非常高的频率下是没有物理意义，但我们仍然会使用它，并想看看随着频率的上升，它与电磁波解的吻合程度如何。接地条件适用于外导体的所有表面、腔壁以及连接二者的表面。

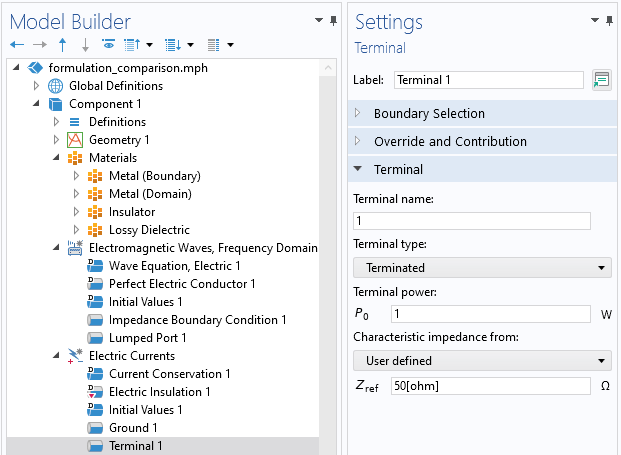
COMSOL Multiphysics^® 用户界面，显示了 终端 > 终止类型。

内导体的表面通过终止类型的终端边界条件进行激励，用于创建与指定阻抗的传输线的连接，如上图所示。它在物理上的解释类似于我们之前在电磁波 接口中使用的集总端口 边界。其余的边界条件，即内外同轴导体之间绝缘体的环形边界，设置为电绝缘。这意味着电场将与该边界平行，这是同轴电缆内部电场的预期解。

我们根据填充腔体的样品材料随频率变化的总损耗来比较这两种方法。下图显示了这两个模型在非常宽的频带上具有一致的结果；从 100 kHz 到近 100 MHz，解都非常一致。预计这两种方法将在非常高的频率下具有不同的结果，但需要注意的是，很难提前估计发生这种情况的频率，具体取决于几何形状、材料属性和边界条件。在实践中，如果您有任何疑问，推荐的方法是建立两个模型并进行结果比较。

电磁波和电流物理场接口的模拟结果比较。在很宽的频带范围内二者具有一致的解。

关于这个模型，我们应该有一个问题，那就是关于我们之前所做的一个假设。我们曾假设，在电磁波 模型中，金属中的集肤深度与导体的尺寸相比较小，进而假设金属域的体积内的场是均匀的，因此不需要求解。所以我们在之前的两个模型中都是通过边界条件对金属域进行建模的。在下一个例子中，我们可以检查这个假设是否正确，并求解导体内的集肤效应。

通过磁场和电场物理场接口求解

第三种方法，我们使用磁场和电场 物理场接口求解。简单的说，这个接口可以被认为是前两个接口的组合，尽管它有一个更加正式的名称：A-V 公式（A-V formulation），并且它对电场具有的独特的定义，详细请阅读博客文章《理论介绍：什么是规范固定》 ”。从计算复杂性的角度来看，这种方法的计算成本最高，因为它在所有域中求解标量电势场和磁矢量势场，如果想在集肤深度非常小的频率下求解金属域，则需要边界层网格。在这篇博客中，我们将避免划分边界层网格，只在 100kHz – 1MHz 频率范围内求解。如果在这个范围内与其他两种方法的结果一致，那么我们就可以合理地推断其他计算量较小的方法是合适的。

关于边界条件，我们可以再次在圆柱体壁上使用阻抗边界条件，其余边界在同轴电缆的横截面处都是磁绝缘 类型，这意味着磁场将平行于这些边界，并且电场没有与边界相切的分量。磁绝缘 边界条件还包括一些额外指定了边界法向电场分量条件的子功能。

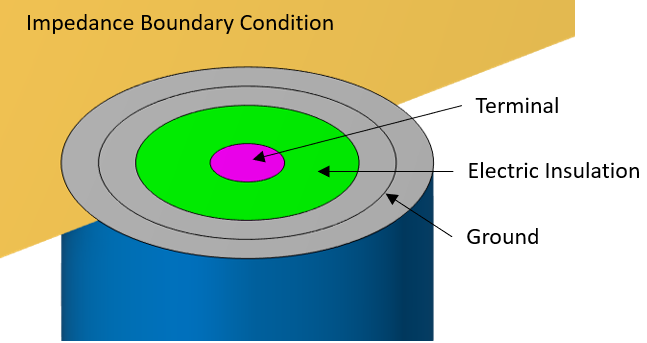
磁场和电场接口中的边界条件示意图。

首先，在内导体的边界上应用终止类型的终端条件，这与电流物理场接口的情况类似。接下来，在同轴电缆内部绝缘体的边界上应用电绝缘 ，最后，在外导体的环形边界以及同轴电缆外部绝缘的周围环形边界上应用接地条件。这样就完成了腔壁和外导体之间的电连接。

在逐渐降低的频率上，使用 磁场和电场接口方法与使用其他方法的结果比较。

在 100 kHz – 1 MHz 频率范围求解这个问题，并将结果与之前的结果进行比较，如上图所示。我们看到了近乎完美的一致性，因此有理由说使用电流物理场接口或电磁波 物理场接口是等效的，而且通常更优越，因为它们的计算成本较低。通过磁场和电场 模型，我们可以应用电压和接地边界条件，正确理解这些术语在非零频率下的解释，并可以获取金属域中的损耗。该数据证实了以下假设是正确的，即与充满空腔的介电材料内的损耗相比，金属中的损耗相对较小，同时也进一步验证了其他方法的正确性。

其他方法

在这篇博客中，我们介绍了三种不同的建模方法，它们在一定频率范围内生成了相同的结果。现在，我们来看看两种其他方法。

使用电磁波，频域 物理场接口的第一种建模方法可以在 AC/DC 模块中的磁场物理场接口精确地再现。该接口提供了相同的阻抗和集总端口 边界条件。磁场接口中的磁绝缘 边界条件在功能上与电磁波 接口的完美电导体 边界条件相同。对于这个特定问题，这两个物理场接口将给出相同的结果。这就提出了一个问题，为什么我们应该使用电磁波，频域 接口而不是磁场接口。

当需要应用不同的边界条件时，两者之间的区别就会出现。我们在这里考虑的情况是，电磁波被限制在一个空腔内，能量只能通过传输线馈入或离开这个空腔。 (这种现象包含在集总端口 特征中。) 这种特殊情况可以使用两个接口等效处理。相反，如果我们想考虑电磁波没有被限制或完全消散在域内，而是可以向周围辐射的情况，那么需要电磁波 物理场接口的一组独特的非反射条件来截断建模域。我们可以使用散射边界条件，或者完美匹配层 域条件来模拟非反射边界，相关例子可以参阅我们的博客文章《使用完美匹配层和散射边界条件解决电磁波问题》。

还值得注意的是，无论是电磁波，频域 物理场接口还是磁场物理场接口，我们都可以求解金属域内的场和损耗，并在 100 kHz – 1 MHz 频率得到与磁场和电场 物理场接口相同的解。这就提出了一个问题，为什么我们应该使用磁场和电场 物理场接口？在可能存在明显感应电流的模型中，它的优势在于可以求解 100 kHz 及以下的较低频率。就像我们这篇文章中的示例模型中显示的那样，仅考虑传导电流和位移电流则可以很好地通过电流物理场接口求解。

最后，让我们看看是否可以通过电流物理场接口更简单的解决这个问题。虽然我们模拟的是绝缘体和有损介电材料中的电场和电流，但现在让我们来看看是否可以忽略绝缘体中的场。尽管绝缘体中存在位移电流，但这些电流尤其在较低频率下并不占主导。也就是说，如果频率范围足够低，电流模型可以仅在介电材料样品中求解。默认情况下，现在绝缘材料的边界全部为电绝缘。

下图显示了文中介绍的所有 5 种方法的比较。可以看到，最简单的方法在较宽的频带上可以得到与其他方法基本相同的解，而且计算成本更低。

所有 5 种方法的比较。

结束语

通过文中演示的建模示例，我们可以得出以下结论：针对某些特定问题，用于求解麦克斯韦方程组的不同物理场接口（不同方法）可以在较宽频率范围内产生几乎相同的结果。但需要注意，这些接口之间重叠的频率适用范围很大程度上取决于材料属性、边界条件和所模拟的几何形状。

当您不知道应该使用哪个电磁物理场接口进行求解时，需要比较几种不同的方法，就像我们在这篇博客中所做的一样。这样做的好处是，您可以为您的仿真找到一种计算效率更高的方法。

文中介绍的模型文件可从 COMSOL 案例库中下载:

获取教程模型

]]>

使用集总模型简化电流仿真

Mon, 27 Feb 2023 02:18:49 +0000

你有没有遇到过这样的情况：想要通过仿真分析连接到诸如电容器、电阻器和电感器等集总电路元件导体内的交流电流分布，但又不想对集总电路元件的几何结构进行非常精确地建模？ COMSOL 软件 AC/DC 模块中内置的一系列功能可以帮助您处理这种情况。您可以将包含真实体积的导体模型与电路元件的近似模型或集总模型相结合。让我们来看看如何做到这一点!

带铜线和电容的电路板模型设置

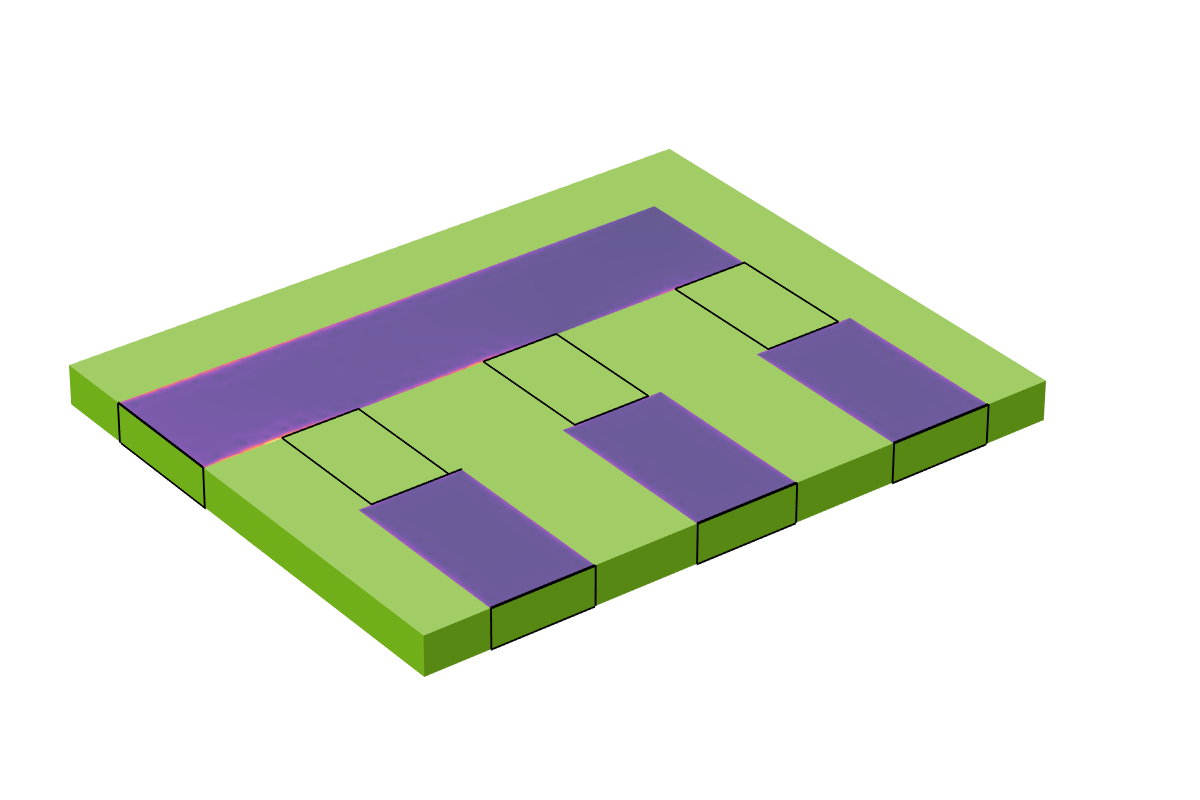
假设你有一块 1.5mm 厚的印刷电路板（PCB），它类似于一个三明治结构，其底部是导电的基底层，顶部为 200µm 厚的覆铜层，中间是电介质。在这块电路板顶层的导线之间，焊接了几个表面贴装电容，如下图所示。其中一条铜走线被激励，由于三个电容器的电容不同，信号将在输出端之间被分割。在 100kHz 左右的工作频率下，集肤深度将与铜的厚度相当，因此我们应该对铜导体的体积以及电介质和空气的体积进行建模，以正确捕捉传输线的行为。(关于传输线建模的更多细节，请参阅我们学习中心的文章《TEM 和准 TEM 传输线建模》）。我们不想建立包含表面贴片电容的真实几何形状的模型，因此只在传输线间引入附加的耦合电容，以观测施加信号的变化。

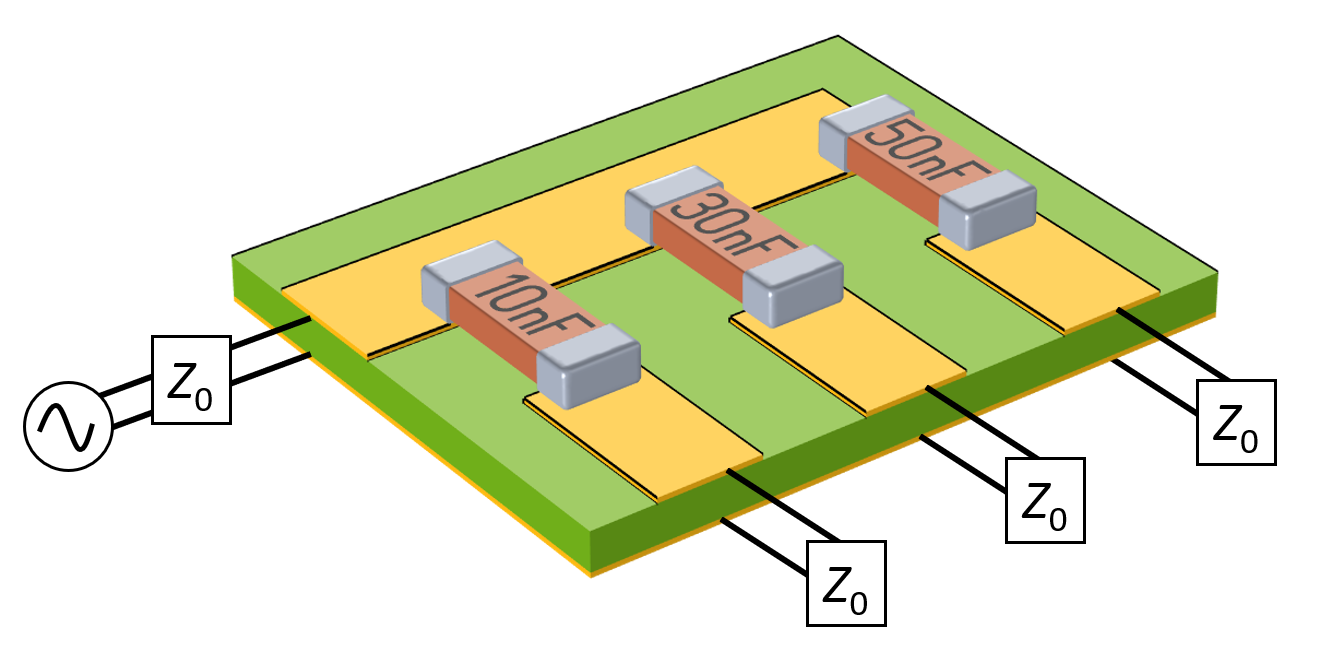
图为一块具有 200um 厚的接地底板、铜迹线和连接铜迹线的三块表面贴片电容的 PCB 板模型。PCB 板上的其他结构不在建模范围内，铜迹线是阻抗已知的信号传输线。

由于导体内部存在明显的集肤效应和邻近效应，因此适用于磁场接口。为了在这个接口中对电容器进行建模，我们使用了集总元件 功能，并将类型设置为用户定义。这个功能应该施加在一个矩形面上，为我们想引入集总元件的区域内架起一个桥梁。这个面需要在几何序列中被勾画出来。

我们需要在集总元件 功能中指定三个基于几何形状的输入端口，集总元件的输入方向必须是一与导体平行的矢量（如下图所示）。也就是说定义器件中流过的电流方向与这个矢量方向相同。集总端口的高度为导电域之间间隙的长度，可用进行电场积分以及计算电压降。集总端口宽度方向为矩形面的正交方向。

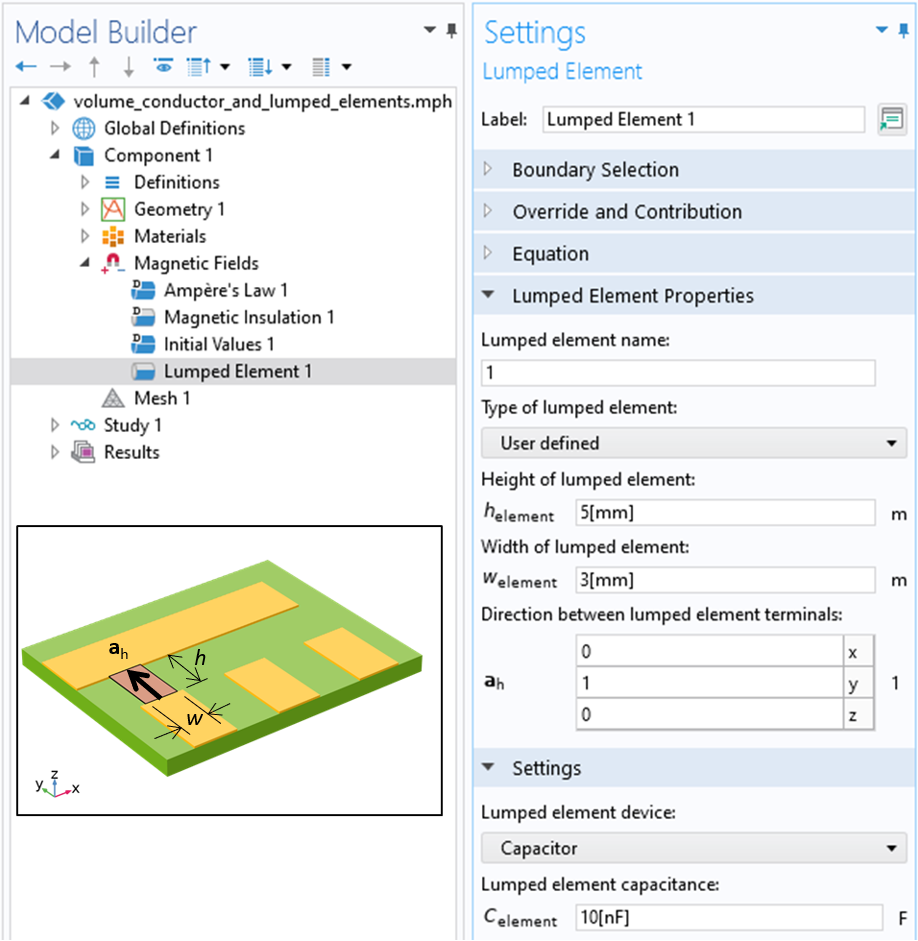
图中显示了选中用户定义选项并指定集总端口高度、宽度和方向的集总元件功能的界面。

除了几何集总元件的几何特征外，我们还需要指定元件随频率变化的阻抗。我们可以在用户定义、电容、电感器、平行 LC、串联 LC、平行 RLC 和串联 RLC 等效阻抗等内置选项之间切换。用户定义 选项允许输入一个与频率相关的复数表达式，这样做可以将一个任意的等效电路添加到一个频域模型中。

按照这个模型的激励，我们可以认为是在模拟 4 条阻抗已知的、连接接地平板和铜迹线的信号传输线。为此，我们可以使用集总端口 功能，并将其类型设置为用户定义。在使用和功能上，集总端口 功能与集总元件 功能几乎相同，唯一的不同是它允许施加激励并监测S参数。

集总端口的类型也可以被设置为电路，这样就可以通过电路接口将任意复杂的集总电路元件组合引入模型中。对于频域模型，使用电路类型在功能上与使用包含用户定义 的频率相关阻抗的集总元件 功能相同。另一方面，对于时域模型，需要使用电路接口添加集总电容或电感。

在设置方面，需要注意模型的边界条件。我们只对电路板和传输线的一小部分进行建模，并将假设周围环境对建模域不产生影响；也就是说，我们将忽略周围结构的任何串扰。我们选择将模型放置在一个更大的空气域内，沿其外侧使用理想磁导体边界条件，模拟一个绝缘的外壳。关于这一点的深入讨论，请参阅我们的博客 “如何为线圈建模选择边界条件“。

评估结果

在 100kHz 的工作频率下求解这个模型后，我们可以评估 S 参数并绘制导体中的电流，如下图所示。观察集肤效应和由集总元件引入的电容耦合的电流的拆分情况。由模型结果可知，我们已经在模型表面利用集总元件实现了电流通路。

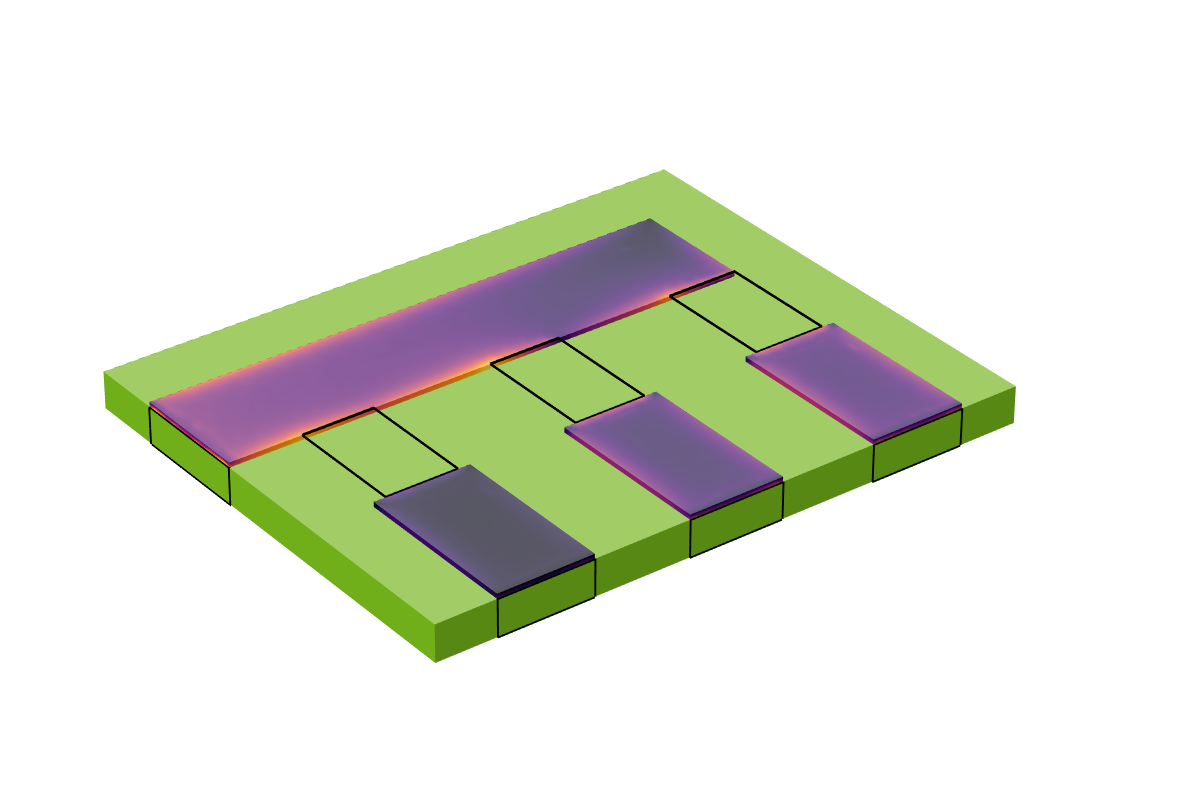
铜导线中的电流分布图。

在更高的频率下求解

如果将工作频率提高到 10MHz 会发生什么。在这个频率下，集肤深度大约是迹线厚度的 1/10，所以不再需要对铜迹线的内部体积进行建模。我们可以在铜迹线所有边界上使用过渡边界条件。这样做是合理的，具体原因请参阅博客 “如何模拟时变磁场中的导体“。通过只求解空气和电介质内的磁场，我们以较少的总自由度解决了问题。现在有可能将集总端口和集总元件从用户定义 类型切换到均匀类型。由于施加这些边界的面现在两边都是导电边界，均匀类型的设置将自动确定端口的宽度、高度和方向。

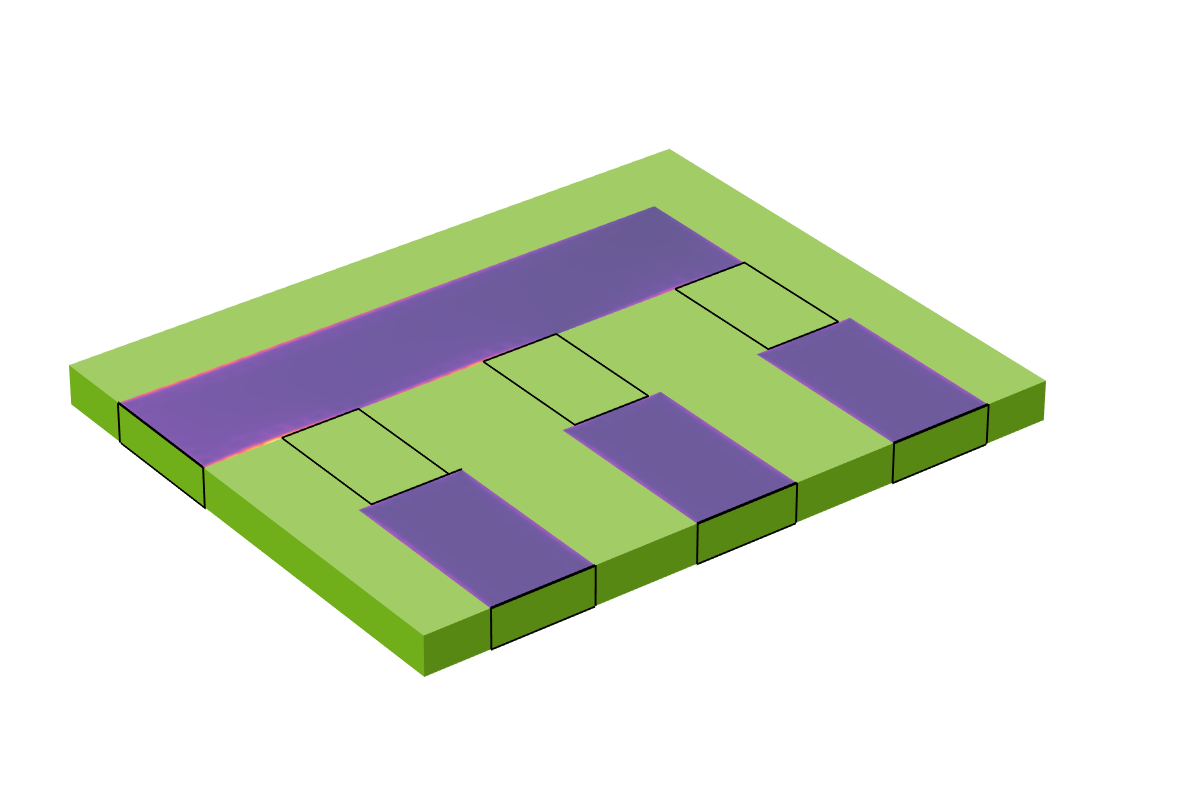
在更高的频率下，不需要对导体的内部进行建模，可以使用 过渡边界条件，表征电流在导体的表面流动。

求解更薄的导体层

在讨论的最后，让我们来看看如何对较薄的铜线进行建模。随着铜线厚度的减小，用于划分网格的结果单元变得更小，这就增加了计算成本。可以通过使用过渡边界条件 避免建立铜迹厚度的几何模型，可以将过渡边界条件 施加在内部边界上，也就是说，边界上的场是在两侧求解的。这使得我们可以将迹线建模为一个几何厚度为零的边界，这进一步减少了模型的自由度，尽管我们可能希望在迹线上有稍微精细的网格。在这样的模型中，不包括由于迹线的有限高度而产生的电容效应，但我们可以合理地假设它们很小。

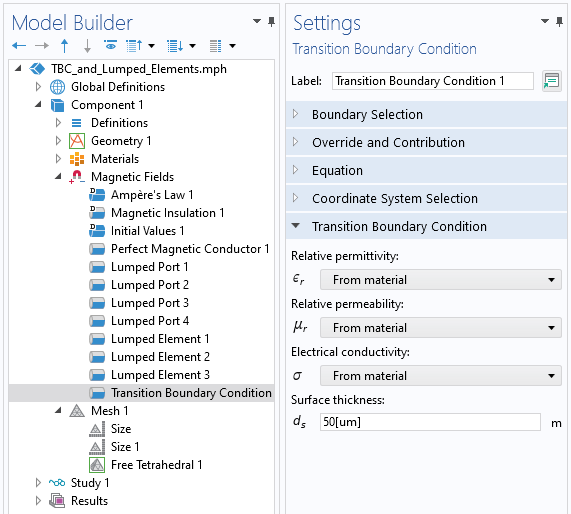
过渡边界条件的用户界面截图，它根据材料属性和厚度计算内部边界的损耗。

使用过渡性边界条件的结果。电流在几何厚度为零的表面上流动。

结束语

这篇博客，我们介绍了如何使用集总单元 功能结合固体导体建模，建立一个等效电路元件。然后，讨论了另外两种情况：当集肤深度非常小时，通过过渡边界条件 对固体导体建模，以及通过过渡边界条件 对非常薄的固体建模，所有这些都与集总单元功能相结合使用。这些建模技术对任何模拟电路板或想在其电磁模型中包含集总电路元件的应用都很有用。值得一提的是，以上技术不仅可以在 AC/DC 模块的磁场公式中使用，也适用于 RF 模块的电磁波、频域 公式。

下载教程模型

]]>

三相输电线路中的损耗

Tue, 26 Jul 2022 02:31:45 +0000

我的一位同事提出了一个关于三相输电系统损耗的有趣问题。事实证明，输电线中导体的某些几何排列方式会导致导线之间的损耗不平衡，即使结构看起来是对称的。在这篇博客中，我们建立了一个简单的模型来证明这一点，并将介绍如何验证这个违反直觉的结果。

为什么损耗不平衡？

假设有三根相同的铜线，它们在一条水平线上等距排列，传输三相电，如下图左侧所示。那么，每根电线的损耗是多少？假设导线很长并且横截面恒定，我们将模型简化为二维横截面模型，在频域中求解。我们在 COMSOL Multiphysics^® 软件中对每根导线进行建模，使用线圈域条件，并以复数形式定义相位彼此相差 120° 的三相交流电流。有关三相传输线建模的详细教程，请参阅之前的博客文章电缆建模系列教程。值得注意的是，通过所有三根导线的电流总和为零，因此我们不需要关心沿边界的任何电流返回路径。每根导线内的损耗分布如下图右侧所示。

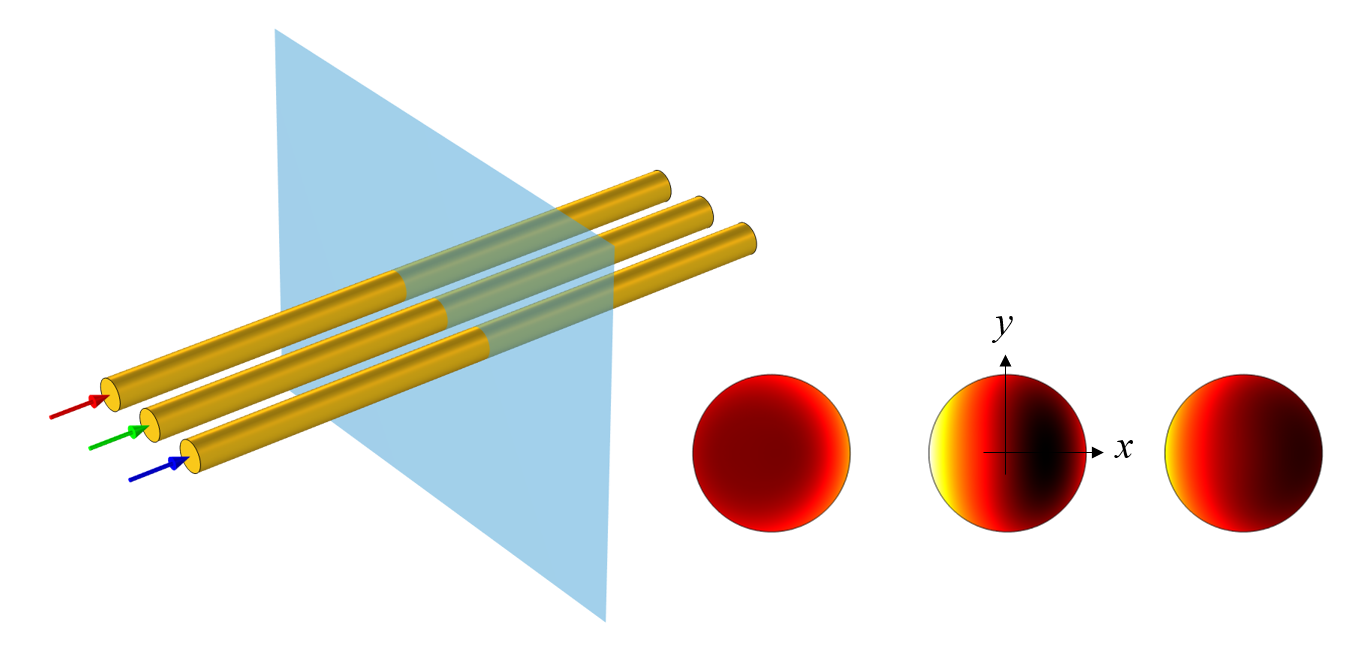
三根通有三相电流的平行导线的示意图，以及横截面的损耗图。

在这副图中，我们可以看到损耗分布关于 x 轴对称，但关于 y 轴不对称。这可能看起来不符合常理，因为导线的几何形状显然是关于两个轴对称。那么，如何解释这个结果呢？

一个损耗平衡的案例

有许多不同的方法来解释这种现象。这里，我们先改变几何，使之更加简单、易懂，然后再研究如何影响计算结果。我们把导体重新排列成一个等边三角形排列，如下左图所示。在这种情况下求解后发现，所有导体具有相同的总损耗和相同的损耗分布。另外，还值得注意的是，这些损耗分布是旋转对称的。也就是说，将磁场围绕中心点旋转120°可以得到相同的分布。现在，我们来努力理解为什么磁场是对称的，并看看这将如何帮助我们理解损耗不平衡现象。

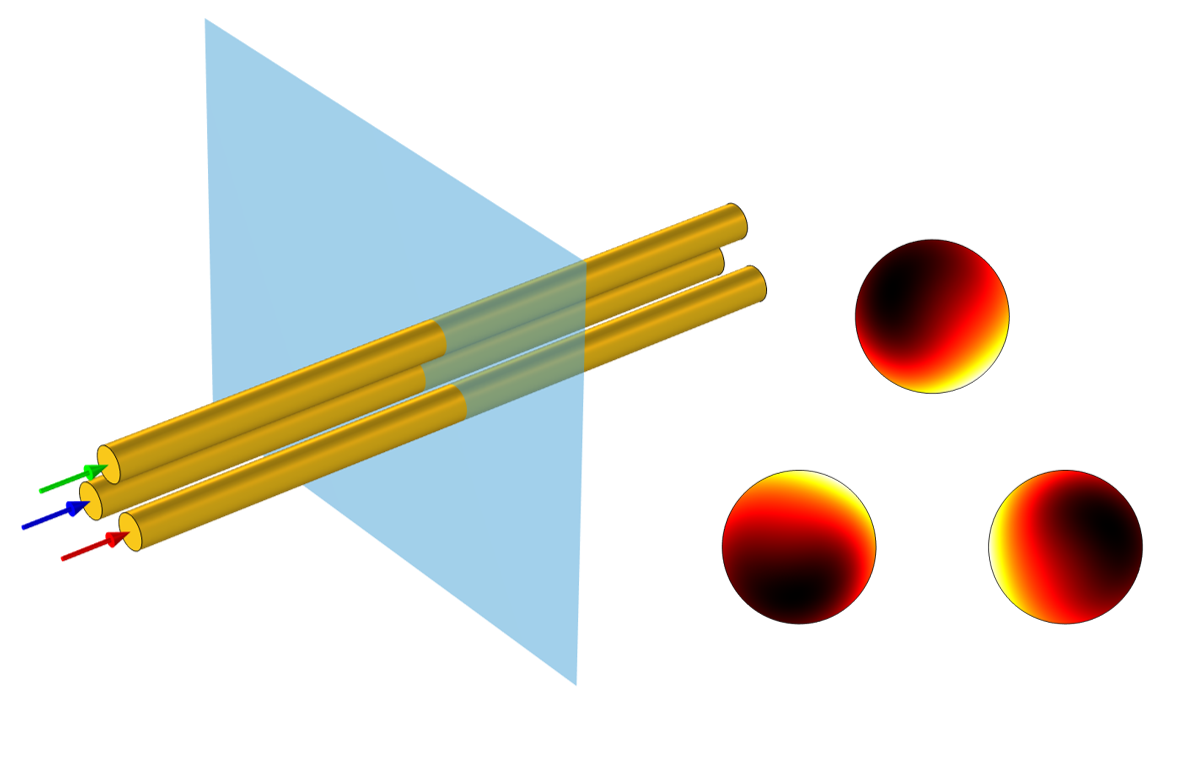
以等边三角形排列的三根导线表现出平衡的损耗。

当交流电流通过单根导线时，所产生的时变磁场会在导线内感应出电流。这些反向感应电流往往会与输入电流反向，尤其是在导线中心，这会导致所谓的集肤效应。除了导线本身的反向感应电流外，邻近效应还会导致输入电流在两个相邻导体中感应出电流。尽管没有正式的证明，我们称其为相邻输电线中的感应电流：

幅值相同，由于相邻的两个导体尺寸和间距相同
相位彼此相差 120°

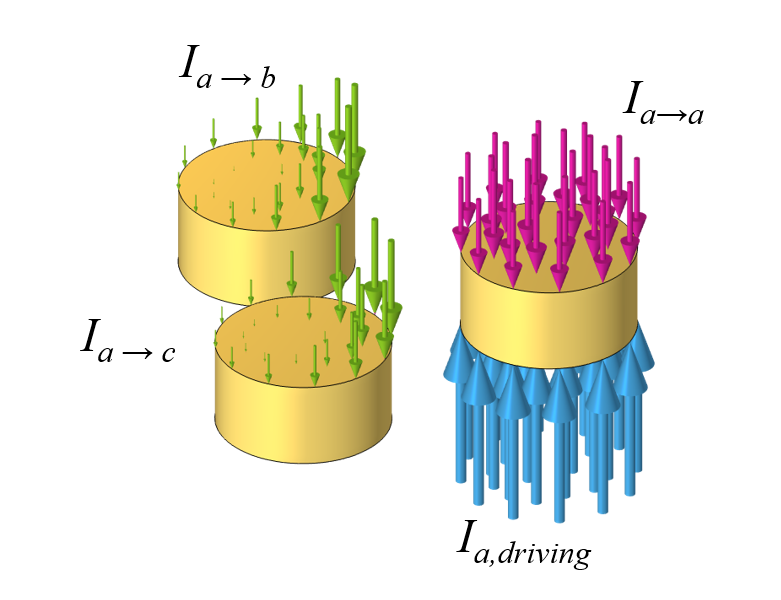
仅查看其中一根导线中的输入电流，它会在导线本身以及两条相邻的导线中产生感应电流。

当三相电流通过所有三根导线时，通过这三根导线中一根导线的总电流是该导线中的输入电流、反向感应电流以及来自相邻导线的感应电流总和，例如，。引起三相电流所需的外加电压与输入电流成正比，由下式给出：，其中是直流线电阻。当使用线圈特征描述这些导线时，方程组中会添加一个额外的全局方程。这将求解能产生所需总电流的电压。每根导线的总损耗由下式给出：，其中电流和电压是复数形式并且相位相差 120°。

现在，让我们在复平面中绘制这些电流，这可以帮助我们观察这三个反向感应电流如何加和为总电流。实际上，我们并不知道这些项的真实幅度或相位，但我们知道来自两条相邻导线的感应电流的相位彼此相差 120°。我们还可以合理地假设电流的相对大小为：。有了这些信息和假设，我们就能够制作下面草图。

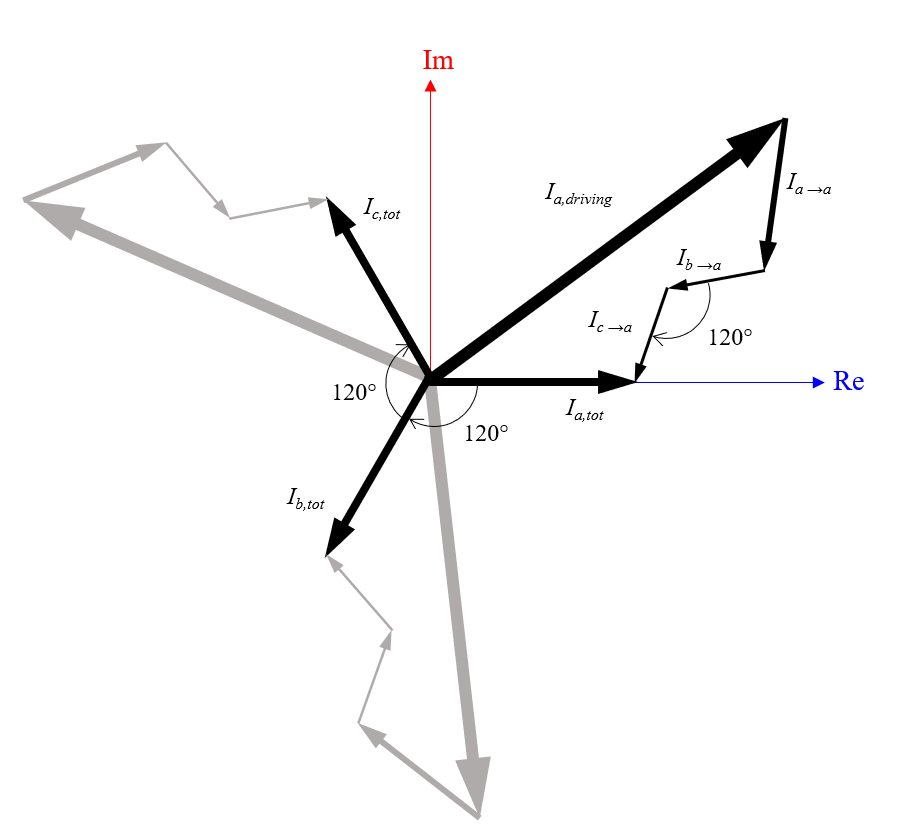
对输入电流、反向感应电流和其他导线感应的电流求和将得出总电流。对于以等边三角形排列的相同导线，这三个电流的幅值相等且相位相差 120°。

考虑施加在所有导线上的复数电压，并考虑当将导线从等边排列变为线性排列时会发生什么。我们将中心导线标记为。反向感应电流，例如，，不会改变，并且从中心导线到外侧导线的感应电流在大小上仍然相等：。从一侧的导线到中心导线和另一根外侧导线的感应电流将不同：和。但是，外侧两根导线之间的感应电流的大小是相同的 ——，并且相对相位保持不变。我们现在可以绘制总和并比较三角形和线性排列。

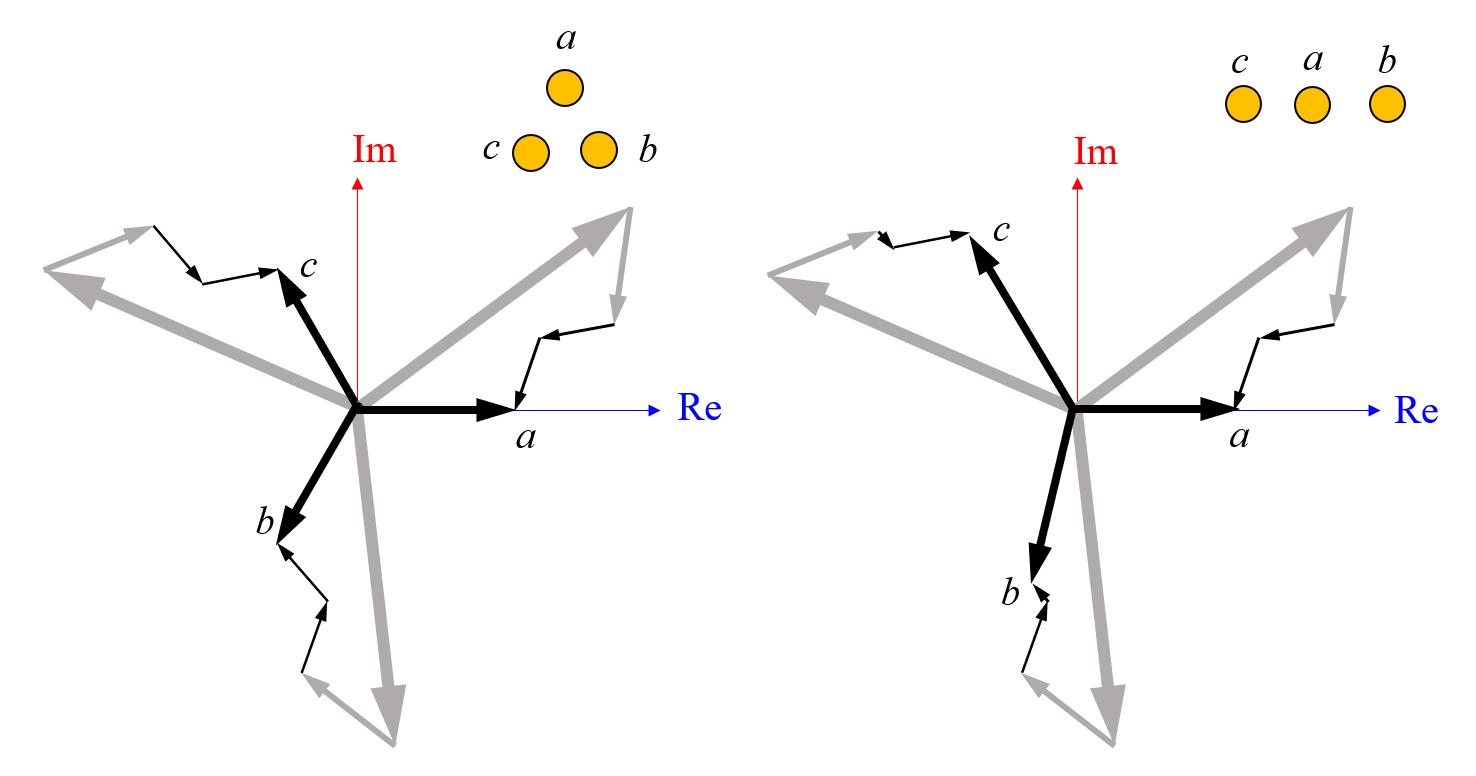
在左侧图中，三角形配置的电流总和是对称的。在右侧图中，电压保持恒定，但导线变为线性配置，因此感应电流的大小不同，对称性被打破。

可以看到，施加三相平衡的电压必然导致电流不平衡。或者，如果我们回到原来的情况并想要获得平衡的电流，那么施加的电压必须都不同。因此，损耗不可能相同。

结束语

如果要对这个系统进行物理验证，最容易想到的方法是测量每根电线的总损耗。外部两根导线上实验测量的总损耗几乎相同，很容易将这种微小差异归因于实验误差。只有当查看数值计算的损耗分布时，如文章开始的图片中那样，差异才会变得更加明显。然而，实心导线内部损耗分布的试验验证将非常困难，而且可能从来没有人做过这样的试验。

还值得注意的是，思考问题有多种不同的方式，这只是其中的一种方式。还可以这样思考，即尽管在初始情况下 x 轴和 y 轴存在几何对称性，但对称条件只允许相位相差 180° 的场，即双重对称。具有相位相差120°导线的解需要三重对称，例如等边排列。同样重要的是，要承认我们在这里展示的不是正式的证明，即使是最基本的结果也应该质疑，无论它们在视觉上多么有吸引力。所以，虽然我们已经提出了一些非正式的证明，但这是否足够？

另一个证明是模型本身。我们开始使用的初始模型很简单：线性布置的三根导线，流通三相电流，通过有限元方法在没有奇点的域上求解。有时，即使是简单模型的结果也会与我们的直觉不一致。这通常会导致人们怀疑模型中的错误，这当然是合理的，因为对每个模型我们都应该带着一点怀疑和严格的验证和确认过程来处理。我们甚至可能会怀疑有限元方法本身，尽管它是数学物理学中最常用和充分验证的方法之一。

最后，我们绝不能落入过于相信直觉的陷阱。科学中一些最瞩目的发现始于意想不到的观察，所以请始终保持开放的心态！

]]>