带标签的博客文章 传热模块
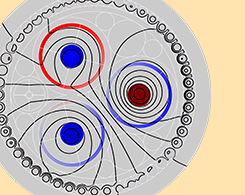
如何模拟地下电缆的电磁加热
在美国几乎所有地方都可以看到架空电缆，但是也有许多我们看不到的地下电缆。地下电缆具有防止风雪侵害的优点，并且由于具有屏蔽性，因此大大降低了电磁场发射。但它们有一个缺点是会大量发热，从而导致绝缘性能下降和失效。
通过仿真研究快速热退火工艺中的传感器性能
快速热退火（RTA）是生产半导体过程中的一个步骤。你可以通过仿真研究相关现象来优化RTA条件。
使用多物理场仿真研究激光与材料的相互作用
为了减轻对高功率激光系统的损害，来自劳伦斯-利弗莫尔国家实验室的一个研究团队使用多物理场仿真来研究激光与材料的相互作用。
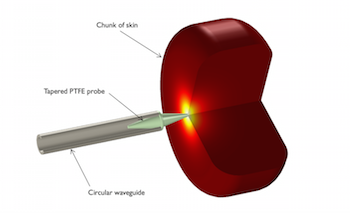
研究用于皮肤癌诊断的介电探针
像介电探针这样的非侵入性工具是一种有希望尽早诊断皮肤癌的方法。了解如何利用仿真来分析它的功能和安全性。
如何计算质量守恒和能量守恒
拟有没有想过如何计算流体流动仿真的质量守恒，或共轭传热模拟的能量平衡？如果是，请继续阅读 >>
使用 COMSOL Multiphysics 模拟马兰戈尼对流
在之前的博客文章中，我们向您介绍了解酒泪现象及其起因——马兰戈尼效应。这种效应是由于两相之间的界面处的表面张力梯度引起的。
使用布辛涅斯克近似模拟自然对流
今天，我们将比较的 布辛涅斯克近似 与完整 纳维-斯托克斯方程 在自然对流问题中的应用。本文介绍了如何在 COMSOL Multiphysics 软件中实现布辛涅斯克近似，以及使用布辛涅斯克近似的潜在优势。 应用示例：方形空腔中的自然对流 在下面的示例中，我们将使用一个耦合了纳维-斯托克斯方程和传热方程的模型来模拟带有加热壁的方形空腔中的自然对流。空腔左壁和右壁的温度分别为 293K 和 294K；顶壁和底壁是隔热的；流体是空气，侧面的长度为 10cm。 我们将使用此模型比较三种不同建模方法的计算成本： 求解完整的纳维-斯托克斯方程（方法1） \rho \left( \frac{\partial \mathbf{u}} {\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \nabla \cdot ( \mu (\nabla \mathbf{u} + (\nabla \mathbf{u})^{T}) -\frac{2}{3} \mu (\nabla \cdot \mathbf{u})\mathbf{I}) + \rho \mathbf{g} 用压力变换求解完整的纳维-斯托克斯方程（方法2） \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u}\right) = -\nabla P + \nabla \cdot ( \mu (\nabla \mathbf{u} + (\nabla \mathbf{u})^{T})- \frac{2} {3}\mu (\nabla \cdot […]
使用传热模块计算角系数
对在 COMSOL® 中计算角系数感兴趣？有一些用于后处理的算子与用于生成表面与表面方程的算子相对应。阅读博客，了解更多内容。