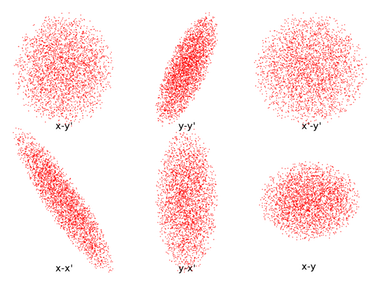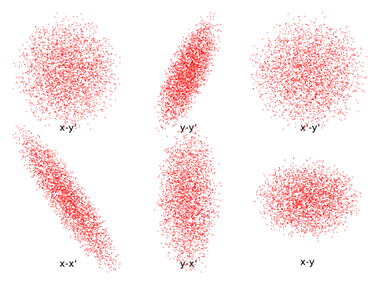束流物理中相空间分布系列 – COMSOL 博客 -

三维带电粒子束的相空间分布取样

Thu, 22 Sep 2016 05:00:20 +0000

在本系列的上一篇博客文章中，我们阐释了在为真实带电粒子束的释放和传播建模过程时，需要考虑的两个必要概念。首先，我们引入了纯数学意义上的概率分布函数，然后探讨了一种特定的分布类型——二维带电粒子束的横向相空间分布。在本篇文章中，让我们结合所学知识，探究如何对这一类分布中的三维粒子束的初始位置和速度进行取样。

回顾椭圆形二维相空间分布

在开始本篇文章前，首先我们来简单地回顾一下在束流物理中的相空间分布系列的上一篇博客文章中，详细介绍过的二维相空间分布。在真实环境中，非层带电粒子束中的粒子占据了相空间的一部分区域，且该区域通常呈椭圆形。二维相空间椭圆的方程式基于束流发射度 ε 和 Twiss 参数，

(1)

\gamma x^2 + 2\alpha x x' + \beta x'^2 = \varepsilon

其中，x 及 x’ 分别表示粒子的横向位置和倾角。Twis 参数进一步构成了 Courant-Snyder 条件，

(2)

\gamma \beta -\alpha^2 = 1

椭圆区域中粒子的实际位置是可以改变的。两种最常见的相空间密度分布是椭圆内的均匀密度分布与最大值位于椭圆中心处的高斯分布，如下图所示。左右两侧的蓝色曲线均为由方程（1）描述的相空间椭圆，其中 ε 表示 4-rms 横向发射度。值得注意的是，对高斯分布而言，仍然有一些粒子游离于椭圆之外。这是因为高斯分布始终没有下降为零，所以无论绘制的椭圆有多大，总会有一些粒子位于椭圆之外。当使用 4-rms 发射度来定义方程（1）中的椭圆时，则大约有 86% 的粒子位于椭圆之内。

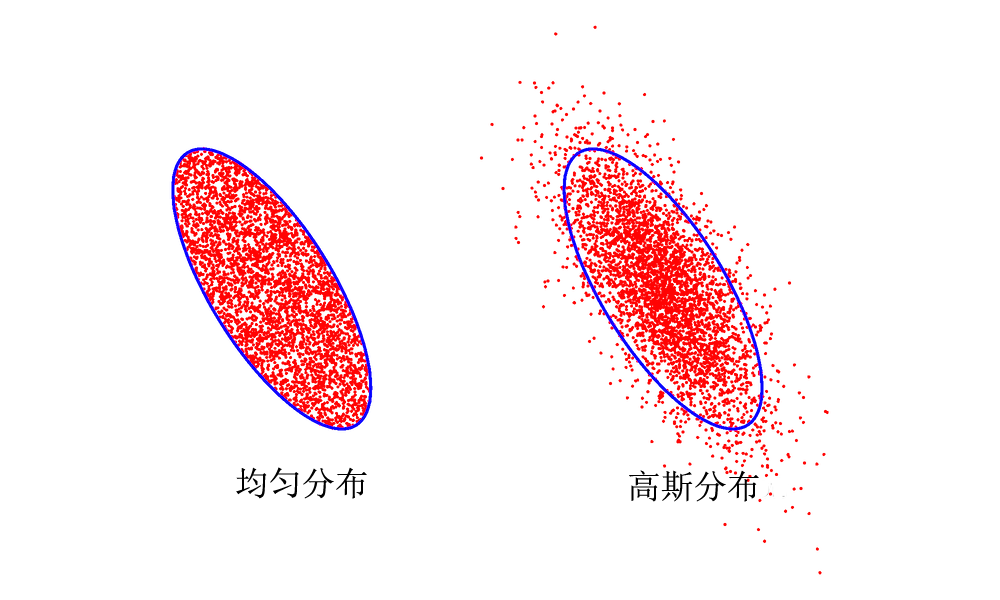
对比均匀分布与高斯分布。

让我们先来考虑一种更简单的情况：在相空间椭圆内的任意一点找到粒子的概率是相同的，而在椭圆外为零。对于这个问题，我们将方程（2）带入方程（1）并求解 x’ 的值

(3)

x' = -\frac{\alpha x}{\beta} \pm \frac{\sqrt{\varepsilon \beta -x^2}}{\beta}

随后可推出以下概率分布函数

(4)

f(x,x') = \left\{
\begin{array}{cc}
C & -\frac{\alpha x}{\beta} -\frac{\sqrt{\varepsilon \beta -x^2}}{\beta} \textless x' \textless -\frac{\alpha x}{\beta} + \frac{\sqrt{\varepsilon \beta -x^2}}{\beta}\\
0 & \textrm{otherwise}
\end{array}\right.

其中，常数 C 取决于椭圆的大小。粒子概率 g(x) 在给定的 x 坐标下可以表示为

g(x) = \int_{-\infty}^{\infty} f(x,x')dx'

若要将方程（3）取实值的位置也纳入考虑，我们可以将方程写为

g(x) = \left\{
\begin{array}{cc}
2C \frac{\sqrt{\varepsilon \beta -x^2}}{\beta} & -\sqrt{\varepsilon \beta} \textless x \textless \sqrt{\varepsilon \beta}\\
0 & \textrm{otherwise}
\end{array}\right.

或将其简化为，

(5)

g(x) \propto \frac{\sqrt{\varepsilon \beta -x^2}}{\beta}, \qquad -\sqrt{\varepsilon \beta} < x < \sqrt{\varepsilon \beta}

假设我们要用方程（4）中的概率分布函数来对一群模型粒子进行取样。具体的步骤是：首先根据方程（5）对粒子的初始横向位置进行取样，随后指定适当的倾角，将粒子限制在相空间椭圆内。一种实现方式是从方程（5）开始计算累积分布函数，然后再使用伪随机抽样的方法。另一种可取的途径是利用方程（5）来定义粒子密度，这时我们可以直接在粒子追踪接口的入口和释放特征中输入粒子密度表达式。输入完成后，系统便会自动完成归一化。

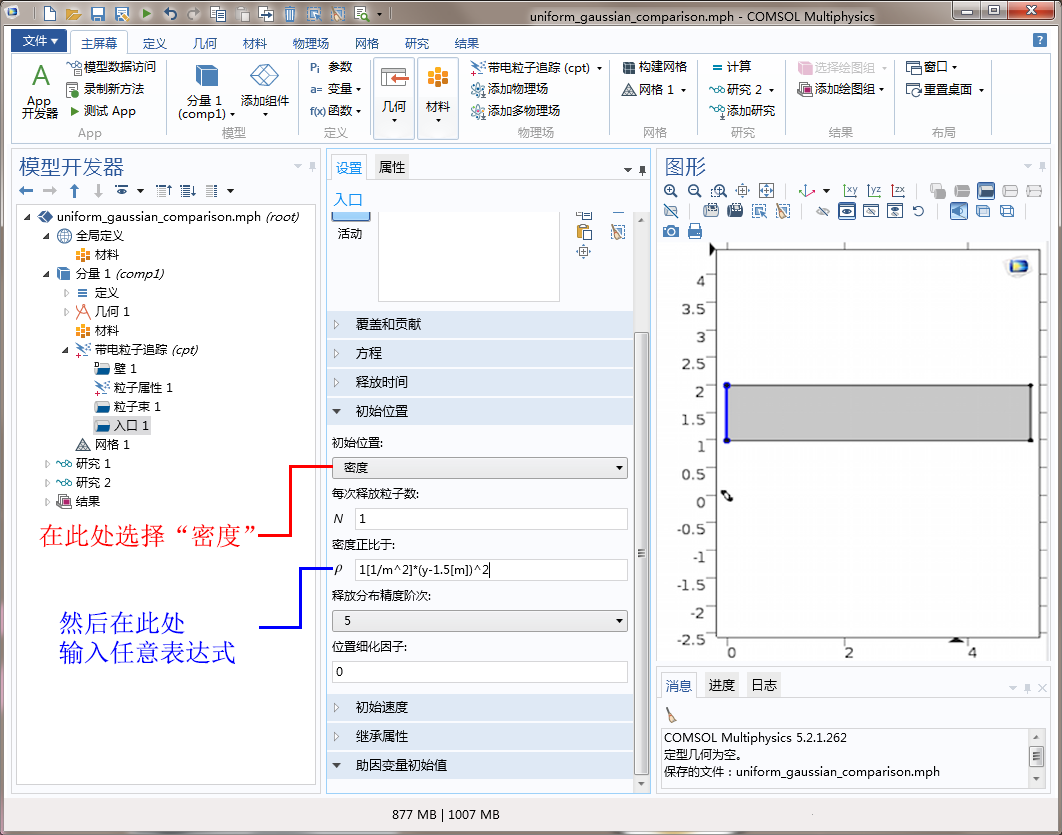
截图显示了如何在“入口”特征中输入粒子密度。

不过，最简便的方法是使用带电粒子追踪 物理场接口中的粒子束 特征。“粒子束”特征可以自动分配相空间中的粒子，同时还能指定粒子束的中心位置、发射度以及 Twiss 参数。

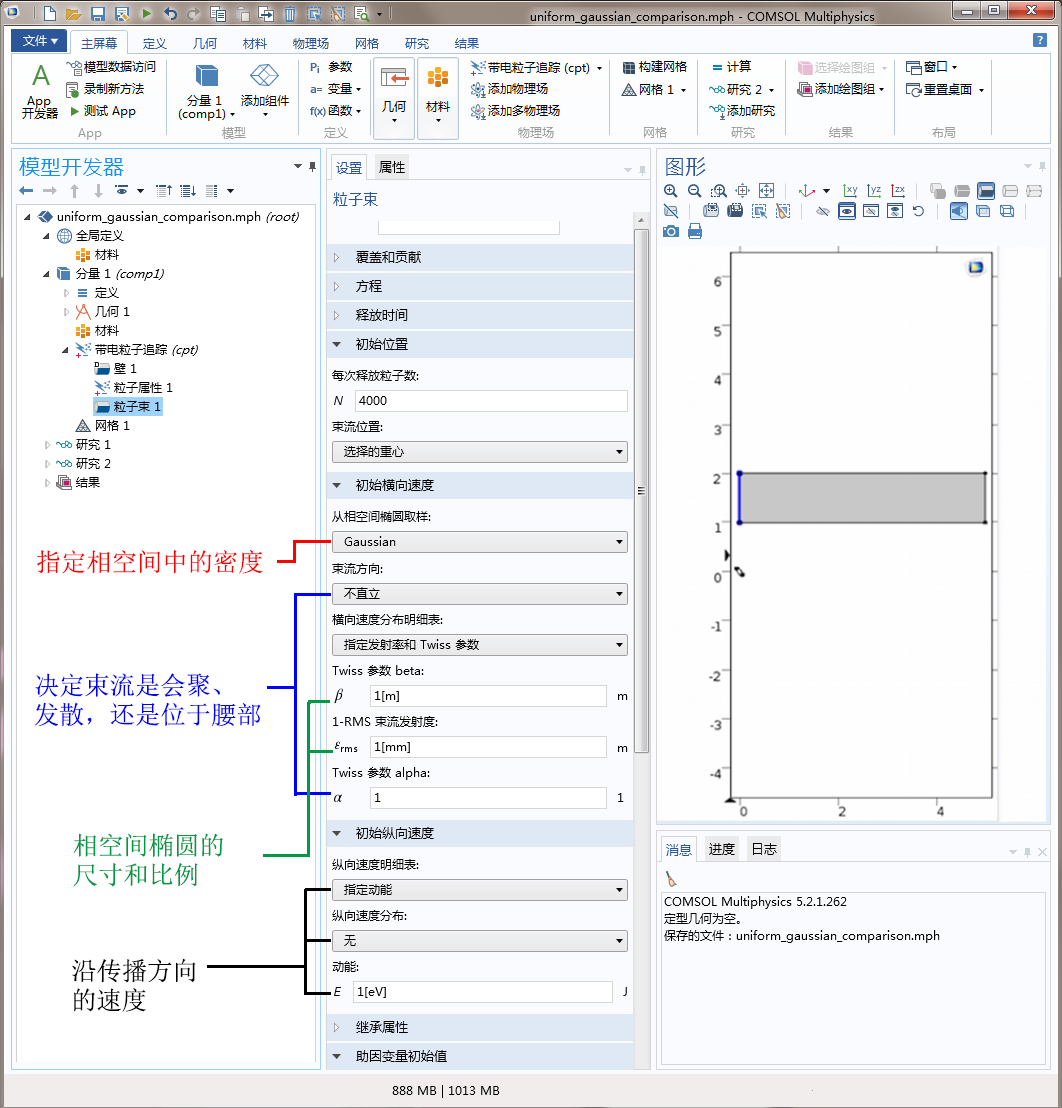
截图显示了如何在“粒子束”特征中输入粒子密度。

模拟三维带电粒子束

到目前为止，我们只对理想化的带状电子束进行了探讨，而忽略了横向位置和速度的面外（y）分量。真正的光束是在三维空间内传播的，并且在两个横向方向上仅延伸了有限的距离。因此，为了绘制完整的束流图像，我们必须引入两个相互正交的横向方向 x 和 y，以及倾角和。

粒子束在三维空间内的传播图像。

相比于二维空间，在三维空间中模拟离子束的释放更加复杂，这是因为在真实的光束中，两个横向方向上的自由度经常会发生耦合。举例来说，假设两个粒子在同一个横向位置上被释放，即 x 坐标和 y 坐标相同。若两个粒子在 x 方向（x’）上的倾角存在大小之分，那么在 x 方向上倾角较大的粒子在 y 方向上的倾角会较小，反之亦然。因此，我们不能只从两个不同的分布中对 x’ 和 y’ 进行取样，因为每个值都会影响另一个值的概率分布。

简而言之，这是因为粒子的横向运动实际上在四维相空间分布中才能进行准确的描述，而不是将两个横向方向当作独立的二维相空间椭圆。由于习惯于在二维或三维空间中观察物体，我们很难呈现出超过三个空间维度的分布情况。

这一点正是“粒子束”特征的最大优势，其设置可专用于对各种内置四维横向空间分布的初始粒子位置和倾角进行取样。常见的四维空间分布包括 KV（Kapchinskij-Vladimirskij）分布、水袋分布、抛物型分布及高斯分布。首先，我们来讨论最简单的分布 KV 分布，然后对这一组中的其他分布类型进行可视化。

在数学上，KV 分布认为束粒子均匀地分布在相空间内的一个无限薄的四维超椭圆体上，其表达式为

\left(\frac{x}{r_x} \right)^2
+\left(\frac{r_x x' -r'_x x}{\varepsilon_x} \right)^2
+\left(\frac{y}{r_y} \right)^2
+\left(\frac{r_y y' -r'_y y}{\varepsilon_y} \right)^2 = 1

其中，r_x 和 r_y 为波束在 x 和 y 方向上的最大值，ε_x 和 ε_y 为与两个横向有关的发射度，r’_x 和 r’_y 为束包络边缘的倾角。

由于四维概率分布函数的可视化比低纬度函数更复杂，通常我们将其投影到较低维度就可以直接实现分布的可视化。KV 分布的一个有趣特性就是，其在任何二维平面内的投影都是一个是均匀密度的椭圆。其在六个平面的投影如下图所示。四维超椭圆体在 x-x’ 及 y-y’ 平面内的投影是倾斜的，因为非零值已指定为每个横向的 Twiss 参数。

六个二维平面内的 KV 分布投影。

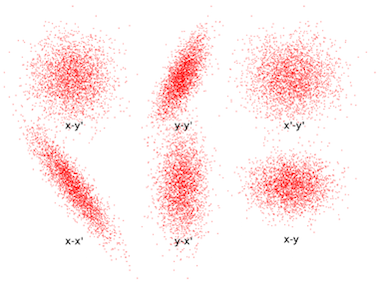
对比上方和下方的两组图。

六个二维平面内的水袋分布、抛物线分布及高斯分布的投影。

从上图中我们可以看到，任意情况下二维平面内的投影都是一个椭圆形分布，但只有 KV 分布中的椭圆被均匀填充。

带电粒子束建模总结

有关带电粒子束建模的系列博客到这里就全部结束了，然而我们到目前为止讨论的，仅是束流物理这一复杂技术领域的一些皮毛。当我们讨论三维横向相空间分布时，未涉及到纵向发射度或与此相关的聚束现象。我们也并未区分讨论在束流传播过程中，可能导致其发射度增加、减少或保持不变的现象。

本系列博客文章旨在介绍如何从概率分布函数中进行随机或伪随机取样，以及这种方法对于捕捉真实的高能离子或电子束所起的重要作用。如您想更加深入地了解束流物理学，参考文献 1~3 有将对您大有脾益。如需获取更多关于上文中讨论的四维横向相空间分布的技术细节（包括从这些分布获取伪随机数量取样的算法），您可以参阅参考文献 4~7. 如需深入了解如何在 COMSOL Multiphysics® 软件中应用这些概念，您可以浏览以下资源或联系我们获取相关指导。

查看有关粒子追踪仿真的其他资源

查看束流物理中的相空间分布系列的其他博客文章
浏览粒子追踪分类中的其他博客文章

参考文献

Humphries, Stanley. Principles of charged particle acceleration. Courier Corporation, 2013.
Humphries, Stanley. Charged particle beams. Courier Corporation, 2013.
Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.
Lund, Steven M., Takashi Kikuchi, and Ronald C. Davidson. “Generation of initial Vlasov distributions for simulation of charged particle beams with high space-charge intensity.” Physical Review Special Topics — Accelerators and Beams, vol. 12, N/A, November 19, 2009, pp. 114801 12, no. UCRL-JRNL-229998 (2007).
Lund, Steven M., Takashi Kikuchi, and Ronald C. Davidson. “Generation of initial kinetic distributions for simulation of long-pulse charged particle beams with high space-charge intensity.” Physical Review Special Topics — Accelerators and Beams, 12, no. 11 (2009): 114801.
Batygin, Y. K. “Particle distribution generator in 4D phase space.” Computational Accelerator Physics, vol. 297, no. 1, pp. 419-426. AIP Publishing, 1993.
Batygin, Y. K. “Particle-in-cell code BEAMPATH for beam dynamics simulations in linear accelerators and beamlines.” Nuclear Instruments and Methods in Physics Research. Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 539, no. 3 (2005): 455-489.

]]>

二维带电粒子束的相空间分布和发射度

Mon, 19 Sep 2016 04:46:22 +0000

在“束流物理中的相空间分布”系列博客中，我们介绍了概率分布函数（probability distribution function，简称 PDF）的含义，以及 COMSOL Multiphysics® 软件中的多种取样的方法。若要探究离子束和电子束是如何在真实环境中传播的，那么有关 PDF 的专业知识是必不可少的。在本篇文章中，我们将重点探讨相空间 和发射度 的概念，以及如何利用他们来描述束流离子或电子的释放问题。

离子束和电子束

离子或电子束指的是动能几乎相同、沿近似同一方向运动的粒子组成的集群。通常情况下，每个粒子的总动能比常温下粒子的热能大得多，因此粒子束拥有极佳的方向性。

首先我们来观察带电粒子束的二维图像。我们用 z 轴正方向表示束流传播方向（轴向），用 x 轴表示与传播方向垂直的方向（横向）。虽然一开始您或许会觉得这种表示方式十分奇怪，但是请记住，我们最终的讨论目的是三维束流，到时候您就会发现用 x 和 y 轴表示两个横向方向将会带来很大的方便。

如上文所述，束流的特点在于它是由大量运动方向和能量都近似相同的粒子组成的集群——然而这里的重点正是“近似”！现实中任何束流中的粒子都不可能具有完全相同的速度。事实上，与束流的释放和传播相关的数学问题基本上都涉及到了束流粒子位置和速度的微小变化。

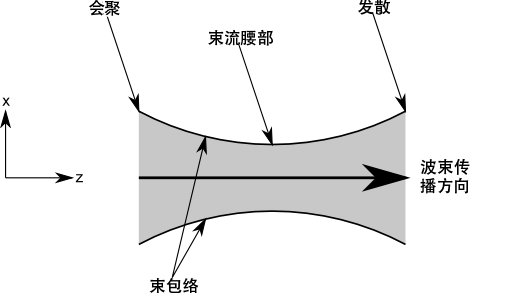
我们可以借助束包络 来表征束流形状，束包络指的是束流粒子的最外层，它能让我们了解束流的形状。如果束流存在一个锐减——即束流粒子的数密度在确定的位置上骤降为零——那么束包络或许只是一个曲线或包含所有粒子轨迹的表面。然而更常见的情况是，束流粒子的密度会在一个较大的距离内逐渐下降，因此束流终点和周围的空白空间并没有明确的界限。在这种情况下，束包络可以被定义为包含绝大部分发射粒子数的曲线或表面，通常包含 95% 左右。若束流的包络在传播方向上会逐渐变小，则此束流为会聚束流；若包络随着束流的传播而变大，则为发散束流。束流腰部 指的是束流刚刚结束会聚并即将开始发散时的位置。我们将在下文中对此进行详细介绍。

比较层束流和非层束流

下图为一个简单的二维电子束，并描绘了其中具有代表性的粒子轨迹，模型暂时忽略了空间电荷效应及外力。坐标轴上添加了标签，以便指示轴向和横向。我们将它看成一个理想的带状电子束——也就是说，电子束在面外（y）方向上无限延伸。这些线指示了束流电子的路径，末端箭头表示各自的速度。每条线上的颜色表示电子在 x 坐标轴（或者说横向位置）上的变化，也称为横向位移。

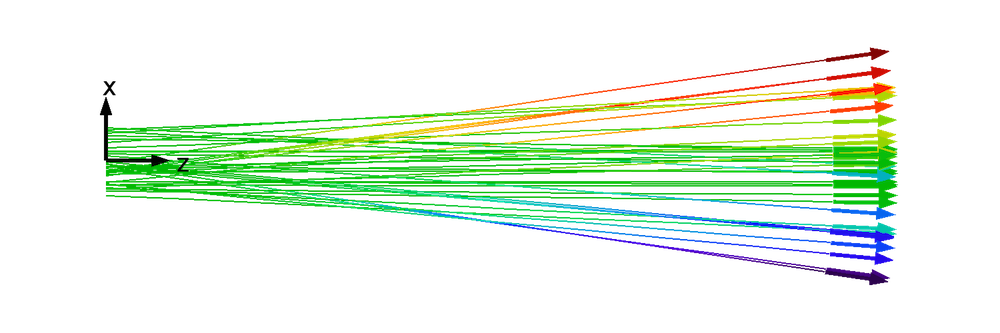
请注意，我们选定原点是为了使 x 轴的起始端位于电子束的中心。同时将中心线或标称轨迹 上的某一点作为起点，这会让横向粒子位置的测量变得十分容易。横向位置的变化率即横向速度 v_x。

从上图和后文的图片中我们可以看出，横向位移和横向速度相当夸张，十分容易观察到。但实际上，与沿电子束轴线的位移和速度相比，它们往往显得极其渺小。

由于具有下列属性，上图中的电子束被称为层束流：

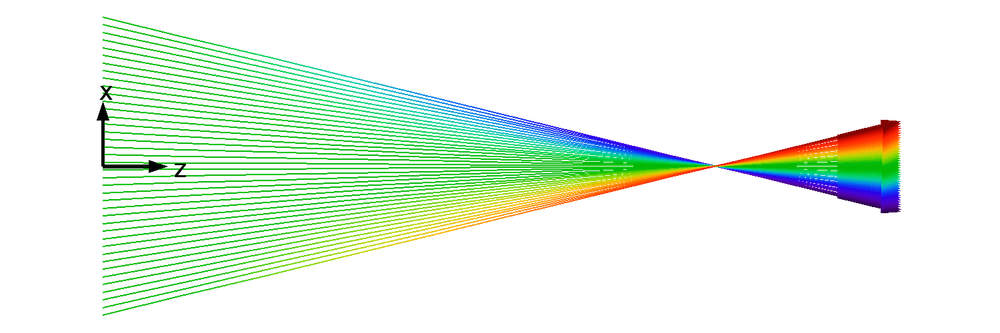
横向位置和速度之间存在一一对应的关系。在任意的横向位置上，电子束粒子的路径不会发生交叉。唯一的例外是会聚电子束，此类束流的全部粒子将交汇于同一点。
横向位置和速度的比例关系是呈线性的。

第二个属性具有重要的意义，因为它保证了之后的过程不会被违背初始属性。在下方图示中，会聚电子束的横向位置和速度之间为平方关系，而非线性关系。初始时（z = 0）粒子轨迹无相交，但在后来某一点上发生了交叉。在图表中的任意一个交点上，一个横向位置可能对应着多个横向速度值，这与第一条属性是相悖的。

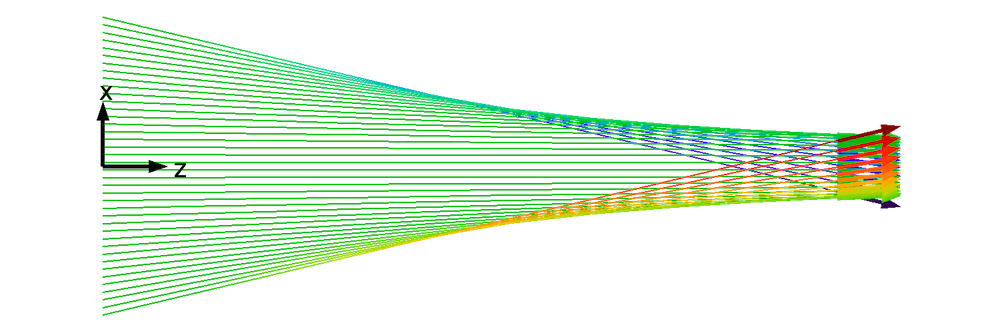
如下图所示，对于层流束而言，除非束流是会聚束流（所有轨迹相交于同一点），否则层束流的粒子永远也不会发生碰撞。

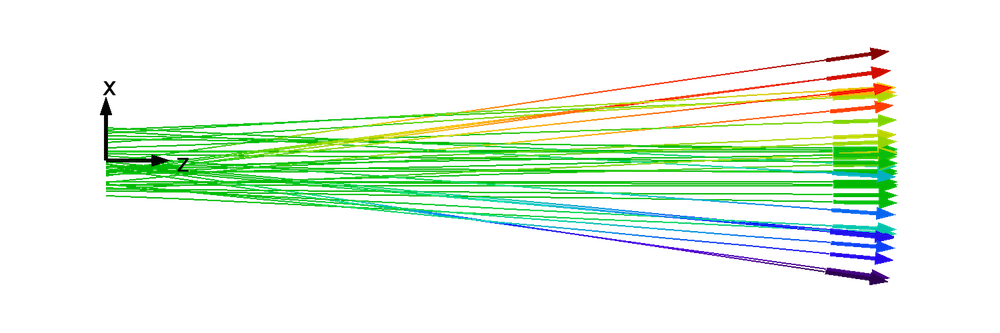
在真实环境中，任意一个横向位置都会存在具有横向速度的粒子分布，并且粒子轨迹之间会不断相互交叉，所以真实的粒子束均为非层束流，上文讨论的层束流只是一种理想情况。下图显示了一种更贴近现实的非层束流的横向速度分布情况。

接下来，为了更好地理解层束流和非层束流之间的差异，我们来观察一下二者的相空间分布。相空间分布具有多种形式，不过在本文中，我们只需要将粒子作为二维空间中的分布的点来进行研究，其中两条坐标轴分别表示横向位置和速度。当然，我们也可以将位置和动量用作坐标轴，这样做虽然会影响分布区域，但不会从根本上改变其形状。借助相图绘图类型，我们可以很方便地在 COMSOL Multiphysics 中绘制上述的相空间分布状况。

首先，让我们观察一下层束流的相图。下图显示了时间 t = 0 时，一条释放边界上的分布情况。

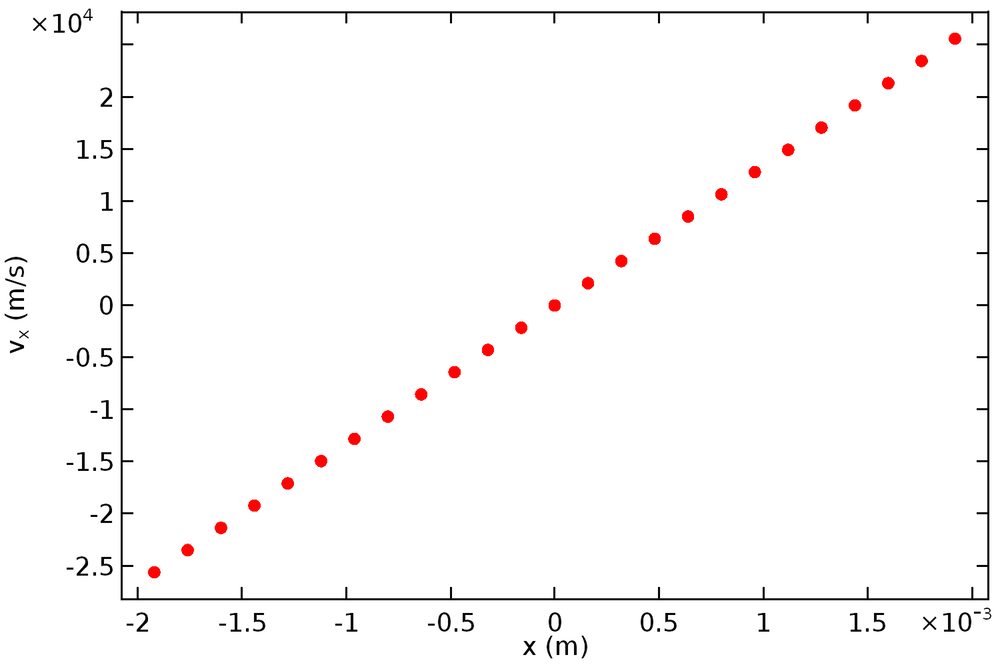
正如我们所料，边界上的点形成了一条穿过原点的直线。（请记住，按照定义，层束流中粒子的横向位置和速度之间存在一种线性关系。）下图为非层束流的相图。

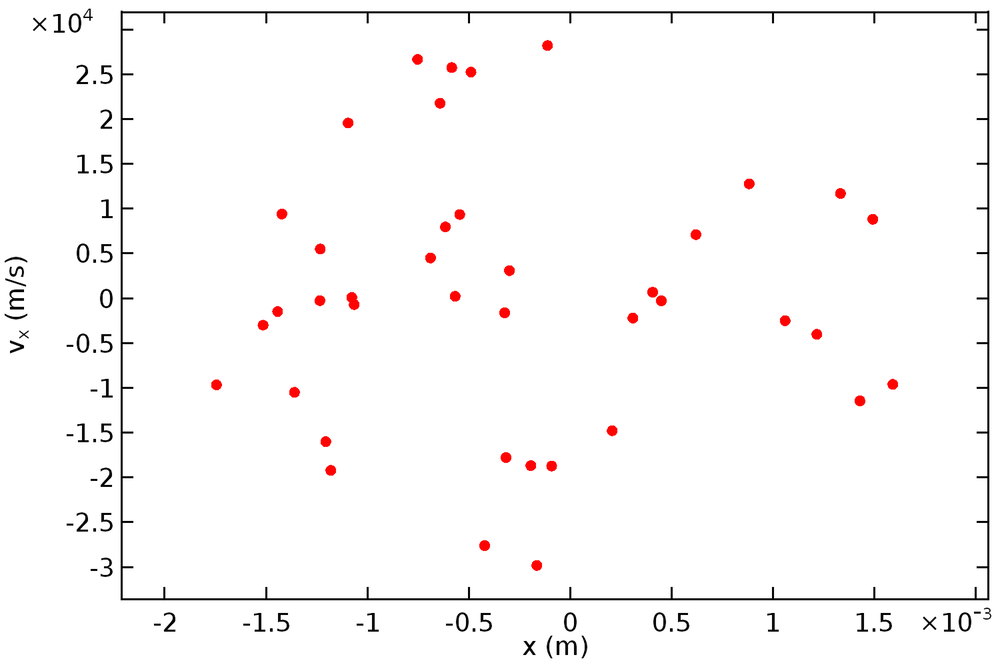
这些点不再位于同一条直线上，而是在以原点为中心的相空间中形成了一片边界模糊不清的云。这些点看似分布随机，位置并不存在任何明显的位置关联。为了更加清楚地了解相位空间分布，我们将此电子束的样本量大幅扩充到了 1000 颗粒子。

现在，我们得到了一张更加清晰的图像：粒子形成了一个相空间椭圆。椭圆中心的粒子最为密集，这说明与靠近束包络边缘的粒子相比，靠近电子束轴线的粒子速度分布范围更广。在束流物理中，这一类椭圆形的分布极其常见，不过在其他情况中，椭圆的比例和取向会发生变化，粒子具体位置也会相应地改变。与束包络的描述一样，相空间椭圆的数密度要么存在一个锐减，要么逐渐下降。在后一种情况中，我们可以对椭圆进行定义，使其包含特定比例的束流粒子，例如 95%。

在真实环境中，多数带电粒子束为近轴，这意味着与纵向速度相比，横向的速度分量非常小。在近轴极限处，我们可以使用粒子的横向位置 x 和倾角对其进行描述。之所以可以将后者看为角，是因为受近轴条件限制。束流粒子的 x 和 x’ 值的分布即迹空间分布，包含该分布的椭圆便是迹空间椭圆。

相空间椭圆的演化过程

上图中的椭圆关于 x 轴和 v_x 轴近似对称。然而，这种情况不会一直持续下去；粒子束传播时，即使没有施加任何力，椭圆形状也会改变，这只是因为沿两条坐标轴的表达式是相互关联的。根据定义，横向速度值为正（v_x > 0）的粒子在相空间中向右移动（x 轴正方向）；同样地，横向速度值为负的粒子将向左移动。下图中的动画演示了当不考虑空间电荷效应时，漂移粒子束的相空间椭圆随时间的演化状况。

若椭圆关于 x 轴和 v_x 轴镜面对称，我们便称此椭圆为直立的。直立的相空间椭圆对应的是束流轨迹上的束流腰部。

束流发射度简介

在束流物理场中，更为方便的做法是在迹空间（x-x’ 平面）中处理问题，而非在 x-v_x 平面或 x-p_x 平面中。一部分原因在于，与横向速度或动量相比，借助倾角 x’ 对束流形状进行可视化能获取更加实用的效果。迹空间椭圆（即位于 x-x’ 平面内且包含迹空间粒子的椭圆）的通式如下

\gamma x^2 + 2\alpha x x' + \beta x'^2 = \varepsilon

其中，参数 γ、β 及 α 被称为 Twiss 参数 或 Courant-Snyder 参数，它们都不是独立的参数，而是共同构成了 Courant-Snyder 条件，

(1)

\gamma \beta -\alpha^2 = 1

物理量也被称为 Courant-Snyder 不变量。

参数 γ、β、α 及 ε 可用于描述迹空间椭圆的形状、尺寸和取向，具体方式如下：

相对于方程（1）使用的其他参数而言，γ 是最常用的的参数，它用于描述束流的比例。ε 恒定不变，γ 增加时，束流占据的空间区域将随之减小（x 值范围缩小），与此同时速度分布随之增大（x’ 值范围扩大）。
α 用于描述迹空间椭圆的倾斜度。在直立椭圆中，α 对应的是束流腰部，且 α = 0。若 α > 0，则为会聚束流；若 α < 0，则为发散束流。
β 也被称为振幅函数 或电子感应加速函数，用于描述束流的比例。ε 恒定不变，β 增加时，束流占据的空间区域将随之增大（x 值范围扩大），与此同时速度分布随之减小（x’ 值范围缩小）。
ε 用于描述迹空间椭圆的大小，又被称为发射度。因为我们正在讨论横向位置和动量，所以将其称为横向发射度 会更加形象具体。

虽然束流发射度能够描述椭圆的大小，但对于发射度和椭圆面积之间的实际关系，存在多个不同的描述方式。其中一种方式是使用椭圆的长半轴长度和短半轴长度的乘积来表示发射度，此时 A = 4πε。下方图表便使用了这一方式，同时还进一步演示了 Twiss 参数是如何影响椭圆的比例和取向的。

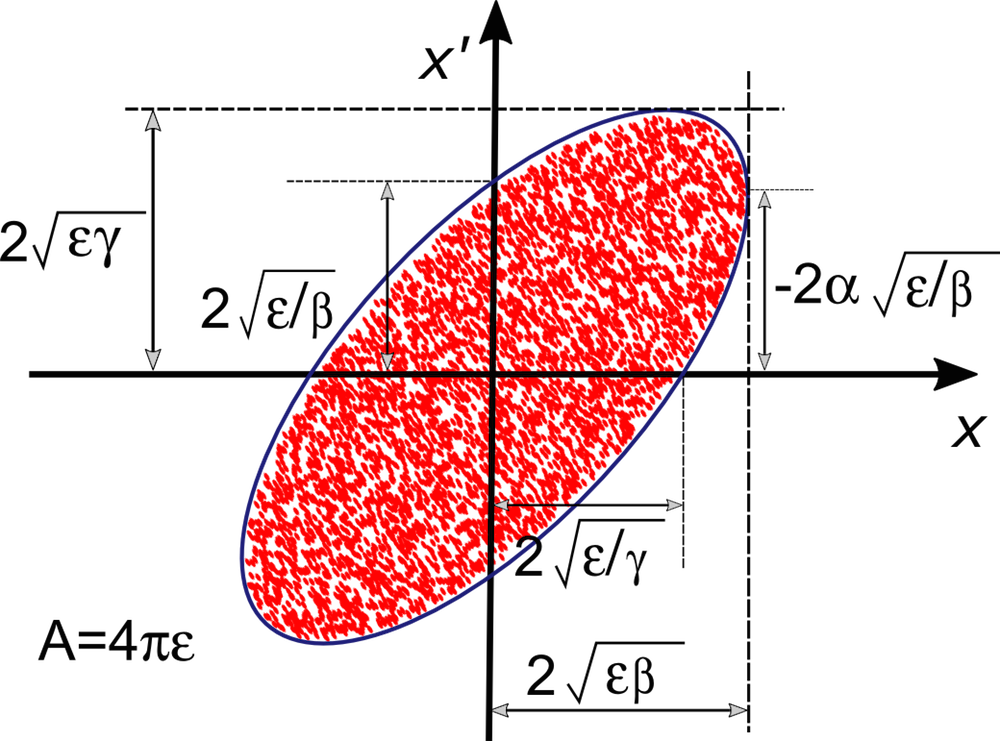
将上述的发射度乘以 4 是一种极其常见的做法，此时 A = πε。一些文献中还会将发射度除以 π，使 A = ε，这一步骤通常并不会特别说明。综上所述，在输入或阅读束流发射度记录时，我们必须确保自己了解使用的是哪一种方式。

从统计学角度解释发射度

到目前为止，我们已经确认了束流发射度的大小代表着被束流覆盖的相空间面积。除了从几何角度解释之外，我们还可以从统计学角度进行解释，即使用全部粒子的平均值来描述发射度。

均方根发射度（或 RMS 发射度）可以被定义为

(2)

\varepsilon = \sqrt{\left\textless\left{(x -(x))}^2\right>
\left\textless\left{(x' -(x'))}^2\right>
– \left\textless\left{(x- (x))\left(x' -(x'))\right>^2}

其中尖括号代表的是算术平均，即

(x) = \frac{1}{N}\sum_{i=1}^{N} x_i

在发射度的几何定义中，人们往往将 RMS 发射度的表达式乘以 4：

(3)

\varepsilon = 4\sqrt{\left\textless\left(x -(x))^2\right>
\left\textless\left(x' -(x'))^2\right>
– \left\textless\left(x- (x))\left(x'-(x')\right)\right>^2}

在 COMSOL Multiphysics 中，为了明确定义发射度，我们采取了额外的预防措施：将方程（2）称为 1-rms 发射度，并将方程（3）称为 4-rms 发射度。如果迹空间椭圆的中心与 x-x’ 平面的原点重合，则，并且方程（2）可以简化为

\varepsilon_{1,\textrm{rms}} = \sqrt{(x^2)(x'^2) -(xx')^2}

其中，方程左侧的项带有下标，是为了更清楚地表明它是 1-rms 发射度。同样地，Twiss 参数的统计定义可以写成（再次使用了简化假设）：

\begin{aligned}
\gamma &= \frac{(x'^2)}{\varepsilon_{1,\textrm{rms}}} \\
\beta &= \frac{(x^2)}{\varepsilon_{1,\textrm{rms}}} \\
\alpha &= -\,\frac{(xx')}{\varepsilon_{1,\textrm{rms}}}
\end{aligned}

由 Twiss 参数的统计定义可以明确看出：当大部分粒子位于迹空间的第二象限和第四象限时，则 α 为正，这说明束流正在会聚。

从统计学角度解释束流发射度还有一个好处：为了确定不规则相空间分布的面积，我们要围绕它绘制一个椭圆，但椭圆会带来一定的模糊性，而统计解释可以消除这种模糊性。同时这种方法也有一个缺点，那就是如果不存在明显的截断距离，远离束流中心的少量粒子会给发射度和 Twiss 参数出现明显的偏差。有时，这些粒子被刻意排除在束流发射度的统计定义之外，例如高斯分布“尾巴”上的粒子。

有关束流发射度的讨论

较小的束流发射度数值，通常与以下束流属性有关：

束流尺寸较小（x 值范围减小）
速度分布较窄（x’ 值范围减小）

人们通常希望尽可能地降低束流发射度。然而，在大多数情况下，束流发射度要么为恒定不变，要么还会增加。目前已有多种技术可实现束流冷却 或者发射度降低，但本系列博客不会对束流冷却技术进行深入的探讨。

为什么我们要如此关注如何降低发射度的问题？排除其他原因不谈，我们一定还记得粒子物理学的基础研究极大地推动了粒子加速器的发展，尤其是在高能物理应用领域。为了让粒子在极高的能量条件下发生碰撞，一定要保证两束粒子相交，而不是让粒子束与静止目标相交。但是，对于两条相交的束流，其碰撞截面远小于一条束流与静止目标相交时的碰撞截面。

出于上述原因，现代粒子加速器的技术目标便是使尽可能多的高能粒子进入一个狭窄空间，从而最大限度地提高碰撞概率。发射度较高意味着粒子扩散的区域面积较大或粒子速度的差异较大，后者会导致粒子占据较宽阔的区域。无论是哪个原因，都不利于提高交叉束流之间的碰撞频率。

扩展到三维环境

到目前为止，我们探讨了什么是粒子束、如何区分层束流和非层束流，以及非层束流的相空间分布是如何与横向发射度的概念联系在一起的。我们还了解到，真实的束流通常在相空间或迹空间中占据有限尺寸的区域，同时其发射度是一个品质因数，且通常在某种程度上与相空间的面积成正比。此外，我们还探讨了束流发射度的两种解释方式：相空间区域内的几何法和以束流粒子的平均值及其倾角进行表示的统计法。

本文仅对理想的二维带状电子束进行了讨论。当扩展到三维时，我们需要考虑两个正交横向上的发射度。真实的束流在轴向上也有一定的速度分布，因此会产生纵向发射度。

在下一篇博客文章中，我们将首次对三维粒子束中的相空间分布进行研究，并学习如何从相空间分布取样，以便对目前为止我们观察到的相空间椭圆进行重现。

了解更多使用 COMSOL Multiphysics® 模拟粒子追踪的内容

查看束流物理中相空间分布系列的全部博客文章
浏览“COMSOL 博客”，查阅更多关于粒子追踪模拟的博客文章

参考文献

Humphries, Stanley. Charged Particle Beams. Courier Corporation, 2013.
Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.

]]>

从概率分布函数中抽取随机数

Thu, 15 Sep 2016 10:02:54 +0000

本系列博客将深入探讨粒子追踪技术在离子束和电子束仿真中的应用。我们首先会介绍概率分布函数（probability distribution function，简称 PDF）的背景知识，并展示在 COMSOL Multiphysics® 软件中对其进行随机抽样的多种方法。在后续文章中，我们还将演示如何基于该数学理论来精准地模拟真实环境中离子束和电子束的传播。

使用概率分布函数的目的

带有能量的离子束和电子束是高能物理和核物理基础研究领域的热门话题，它们也被广泛应用于阴极射线管，医用同位素的生产和核废料处理等领域。对于光束传播的精确数值仿真而言，粒子位置和速度分量的初始值是十分重要的参数。

在粒子追踪仿真中，当释放束流离子或电子时，通常情况下我们需要抽样选取部分粒子作为相空间 中的离散点。不过，在深入探讨什么是相空间，以及离子或电子如何形成相空间之前，我们先来大致了解一下概率分布函数以及如何在 COMSOL Multiphysics 中使用。

概率分布函数简介

首先，我们对相关物理量进行定义。连续随机变量 x 是一个可以取无穷多值的随机变量。举例来说，假设在长度为 L 的线段上随机选择点 x₁，在线段的另一处选择第二个点 x₂。假设这两点是不同的点，我们便可以在该线段上选择第三个不同点，然后是第四个点，以此类推，从而获得无限多个不同的点，如下所示。

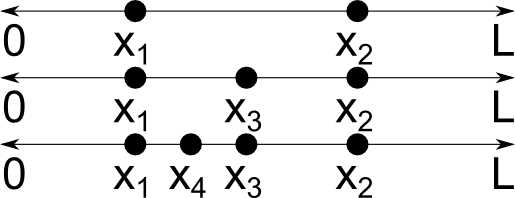
值得一提的是，另一种随机变量被称为离散随机变量，它只能取特定的值。想象你在投掷硬币或从扑克中抽取一张纸牌，这时结果的数量是有限的。

一维概率分布函数 f(x) 又称概率密度函数，主要用于描述连续随机变量的值等于给定值的概率。例如下方的概率分布函数

(1)

f(x) = \left\{
\begin{array}{cc}
0 & x\leq 0\\
1 & 0 \textless x \textless 1\\
0 & 1\leq x
\end{array}
\right.

对变量 x 进行了描述，该变量在开区间（0，1）内取任意值的概率是均等的，但不会在区间外取值。此 PDF 是均匀分布，其绘图如下所示。

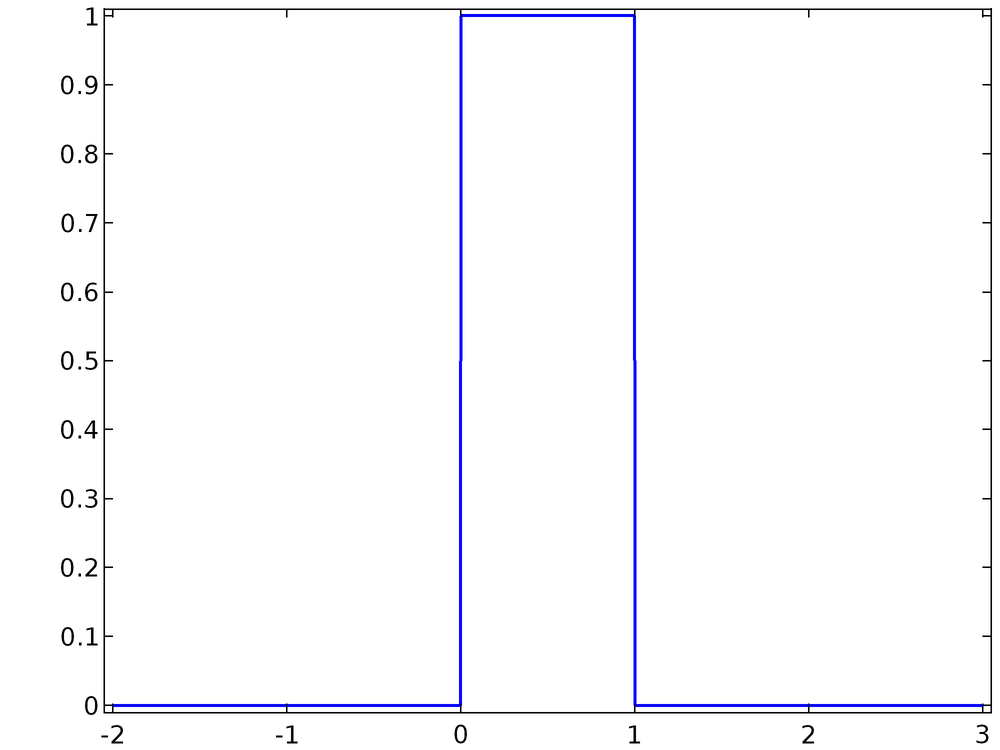
概率分布函数同样可以用于离散随机变量，甚至适用于在某些区间内为连续、在其他区间内为离散的变量。后一类随机变量还可以被当作连续随机变量进行解释，只不过它的 PDF 包含了一个或多个狄拉克δ函数。本系列博客仅讨论连续型随机变量。

若满足以下条件，则 PDF 会被归一化

\int_{-\infty}^{\infty} f(x)dx = 1

换句话说，变量 x 在范围 (-∞, ∞) 内取任意值的总概率为 1。

累积分布函数（cumulative distribution function，简称 CDF） F(x) 指连续随机变量的值出现在区间 (-∞, x) 内的概率。CDF 是 PDF 的积分，表示为

F(x) = \int_{-\infty}^{x} f(x^\prime) dx^\prime

上述定义清楚地表明，如果概率分布函数被归一化，则

\textrm{lim}_{x \rightarrow \infty} F(x) = 1

方程（1）的 PDF 及其对应的 CDF 见下方图表。很明显，PDF已经被归一化了。

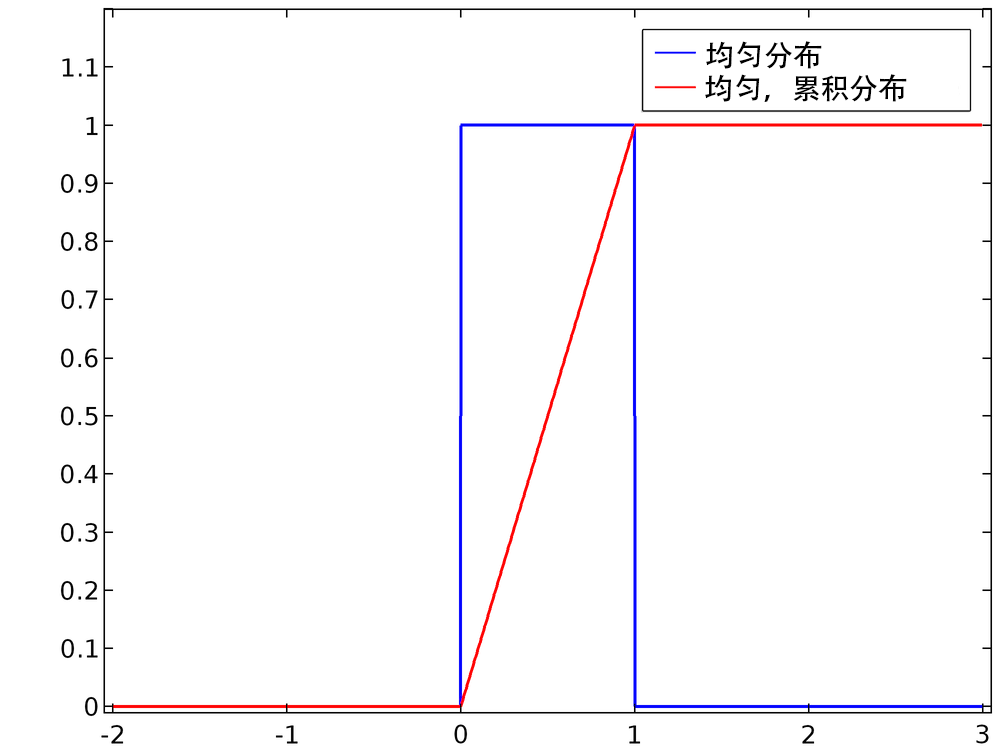
从一维分布中抽样

从均匀分布中随机取值通常是十分容易的。在大多数编程语言中，有非常多的程序可用于生成均匀分布的随机数。然而有时我们可能需要处理更加任意的分布，如下图所示。

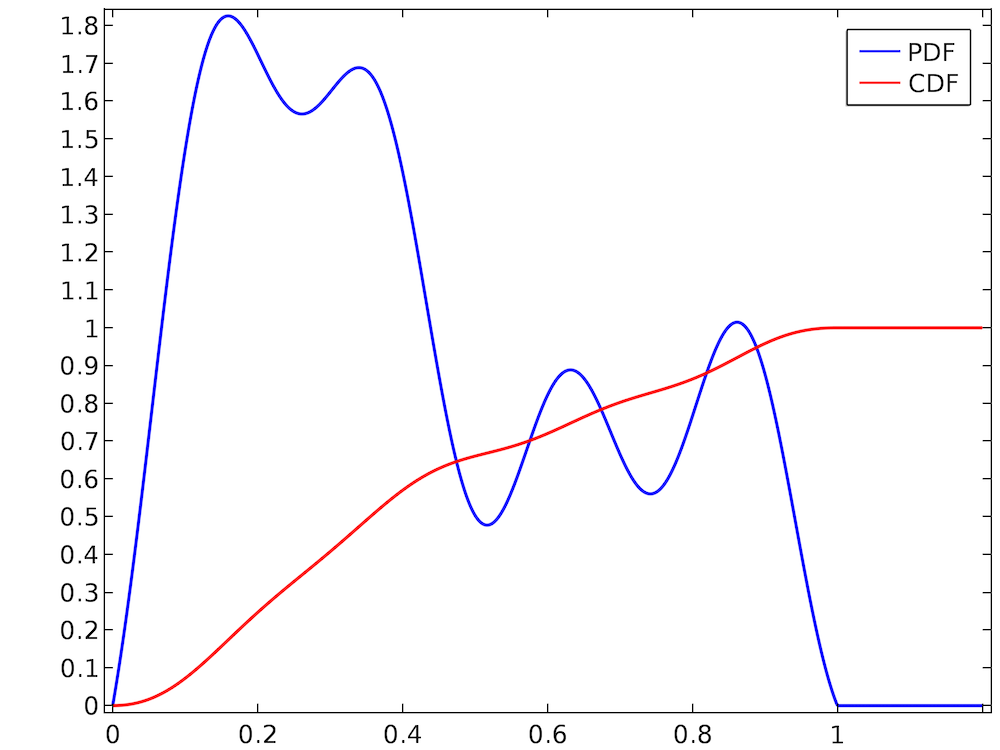
随机数在区间 (0, 1) 内取值，CDF 的最终值为 1，这表示 PDF 已被归一化。但是，随机数的分布显然并不均匀；例如相比于 (0.7, 0.8)，随机数更有可能出现在范围 (0.2, 0.3) 内。在这种情况下，直接使用内置程序对间隔 (0, 1) 内均匀分布的随机数进行抽样，可能并不正确；我们必须想出另一种方法，从这个看似任意的 PDF 中抽取随机数。

为此，我们采用了一种从概率分布函数中取值的最基本方法——逆变换抽样。现在，将 U 定义为 0 到 1 之间均匀分布的随机数。换句话说，U 遵循方程（1）表示的分布函数。接着，为了从（可能不均匀的）概率分布函数 f(x) 中抽样随机数，我们需要执行了下列操作：

若函数 f(x) 尚未被归一化，则对其进行归一化。
求解归一化的 PDF f(x) 的积分，并由此计算出 CDF F(x) 的值。
对函数 F(x) 求逆，得出逆累积分布函数 或者分位数函数 F^-1(x)。由于我们对 f(x) 进行了归一化，所以亦可称之为逆正态累积分布函数，或将其简单表述为逆正态 CDF。
将均匀分布的随机数 U 的值代入逆正态 CDF。

总而言之，当时，F^-1(U) 是满足概率分布函数 f(x) 的随机数。接下来，我们将讨论一个具体案例，帮助您了解如何通过这种途径对不均匀的概率分布函数进行抽样。

示例 1：Rayleigh 分布

Rayleigh 分布 经常出现在稀薄气体动力学和束流物理的方程中，其表达式为

(2)

f(x) = \left\{
\begin{array}{cc}
0 & x \textless 0 \\
\frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right) & x\geq 0
\end{array}
\right.

其中 σ 是待指定的比例因子。如下所示，我们可以证实上方的 Rayleigh 分布函数已被归一化。

\begin{aligned}
\int_{0}^{\infty} \frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right)dx
&= \lim_{x \rightarrow \infty} \left.-\exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)\right|^x_0\\
&= 1-\lim_{x \rightarrow \infty}\exp\left(-\frac{x^2}{2\sigma^2}\right)\\
&= 1
\end{aligned}

它的累积分布函数为

\begin{aligned}
F(x)
&=\int_{0}^{x} \frac{x^\prime}{\sigma^2} \exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)dx^\prime\\
&= \left.-\exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)\right|^x_0\\
&= 1-\exp\left(-\frac{x^2}{2\sigma^2}\right)
\end{aligned}

下图绘制了当 σ = 1 时归一化的 Rayleigh 分布和它的累积分布函数。当 x 逐渐变大时，CDF 显然接近 1。

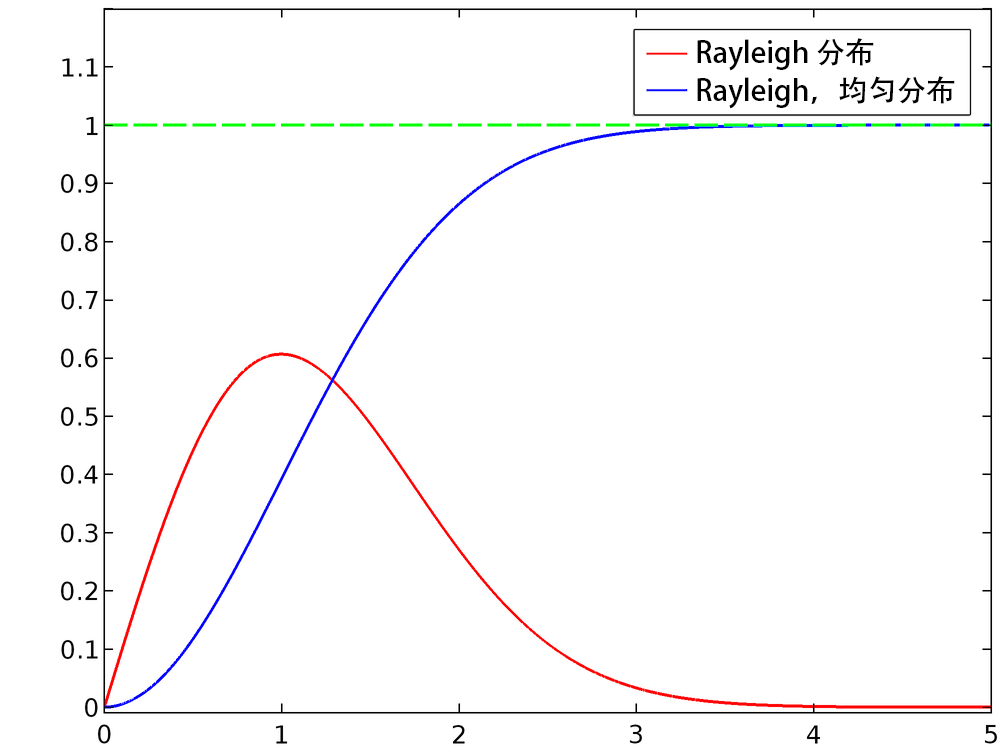
为了计算逆正态 CDF，我们设 y = F(x) 并求解 x 的值：

\begin{aligned}
y &= F(x)\\
y &= 1-\exp\left(-\frac{x^2}{2\sigma^2}\right)\\
\exp\left(-\frac{x^2}{2\sigma^2}\right) &= 1-y\\
-\frac{x^2}{2\sigma^2} &= \log\left(1-y\right)\\
x &= \sigma \sqrt{-2 \log\left(1-y\right)}
\end{aligned}

现在将变量 y 替换为均匀分布的随机数 U，则

x = \sigma \sqrt{-2 \log\left(1-U\right)}

由于 U 在区间 (0, 1) 内呈均匀分布，并且其值当前未知，考虑上述情况，我们通过使 U 和 1 – U 精确遵循相同的概率分布函数，从而进一步简化上方的表达式。由此，我们得到了 x 的抽样值的最终表达式，

(3)

x = \sigma \sqrt{-2 \log U}

接下来，我们将讨论如何在 COMSOL 模型中通过使用方程（3）对 Rayleigh 分布的值进行抽样。

请注意，在计算逆正态 CDF 时，上述分析方法并非总是可行的。对于任何函数的积分，不一定始终存在闭合的解析解，而且累积分布函数的逆函数不一定存在对应的表达式。本文特意选择 Rayleigh 分布作为案例，正是因为我们可以推导出它的逆正态 CDF，而不需要数值或近似方法。

在 COMSOL Multiphysics® 中随机抽样

我们可以借助上述分析结果在 COMSOL Multiphysics 中对任意一维分布（例如 Rayleigh 分布）进行抽样。我们首先来介绍一下可用于从特定类型分布中抽样的内置工具。

在 COMSOL Multiphysics 中，我们有多种定义伪随机数（稍后我们会解释“伪随机”的含义）的方法。例如，您可以使用全局定义 节点或定义节点中的随机函数特征，通过均匀分布或正态分布定义伪随机数。如果使用的是均匀分布，请指定平均值 和范围。若平均值为 μ_u 且范围为 σ_u，则 PDF 为

f(x) = \left\{
\begin{array}{cc}
0 & x \leq \mu_u-\frac{\sigma_u}{2}\\
\frac{1}{\sigma_u} & \mu_u-\frac{\sigma_u}{2} \textless x \textless \mu_u + \frac{\sigma_u}{2}\\
0 & \mu_u + \frac{\sigma_u}{2} \leq x\\
\end{array}
\right.

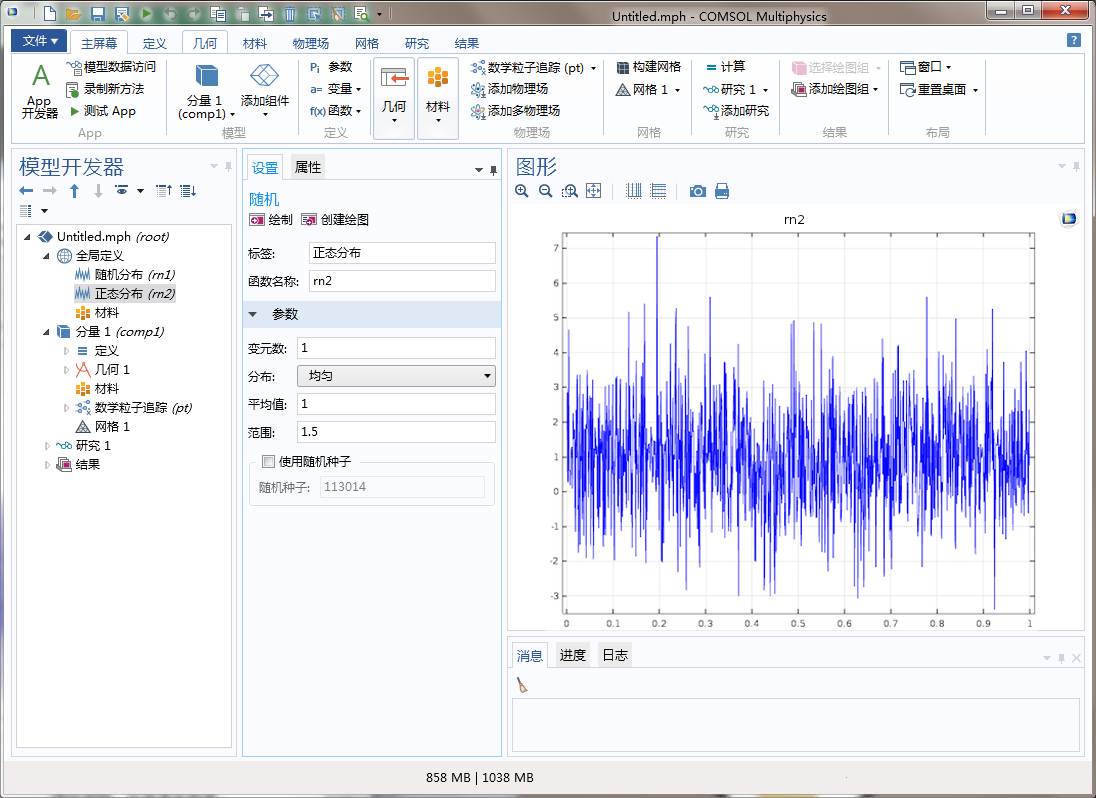
当平均值为 1 且范围为 1.5 时，均匀分布的示例图如下。

当使用正态分布或高斯分布时，请指定平均值 和标准偏差。若平均值为 μ_n 且标准偏差为 σ_n，则 PDF 为

f(x) = \frac{1}{\sigma_n \sqrt{2\pi}} \exp\left(-\frac{\left(x-\mu_n \right)^2}{2\sigma_n^2}\right)

当平均值设为 1，标准偏差为设 1.5，正态分布的示例图如下。与均匀分布的相同点在于，正态分布的曲线呈锯齿状，并且不可预测；不同之处是越靠近 y = 1，曲线上的点就越密集，而越向两边越稀疏。

在默认设置中，平均值为 0，范围或标准偏差为 1，此时两种分布的对比图如下。

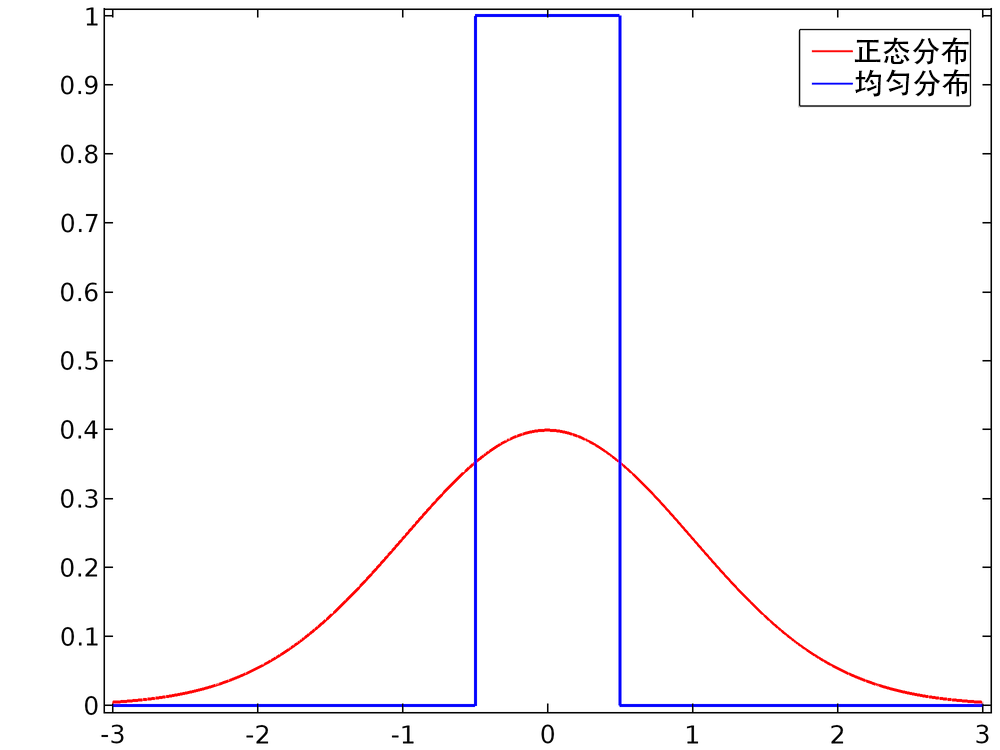
对比范围为 1 的均匀 PDF 和标准偏差为 1 的高斯 PDF。

除了“随机”函数特征，您也可以在任意表达式中使用内置函数 random 和randomnormal。random 函数呈均匀分布，平均值为 0，范围为 1； randomnormal 函数呈正态分布，平均值为 0，标准偏差为 1。

对于方程（3），我们需要在区间 (0, 1) 中均匀抽取一个数 U，有两种方法可以实现这一操作：

使用“随机”函数特征，并将平均值设为 0.5，范围设为 1。
使用内置的 random 函数，并将平均值和范围增加 0.5。

尽管两种方法均是可行的，不过我们将在下文中采用第二种方法。

随机数，伪随机数与种伪随机种子

正如前文所述，采用上述方法的目的是生成伪随机数。伪随机数 指以初始值或种子为起点，通过确定方式生成的随机数。对于内置的 random 函数来说，种子相当于函数的一个或多个变元。对比而言，真正的随机数不能仅仅凭靠一个程序而生成，它来源于自然的熵增——一种本质上不可预测、不可重复的自然过程，例如放射性衰减或大气噪声。

在许多方面，伪随机数使用起来会比真随机数更为方便。伪随机数的重复性特征可被用于排除 Monte Carlo 仿真的故障，这是因为使用同一个种子多次运行仿真可以得到相同的结果，这让识别模型的变化变得十分简单。由于不需要自然熵源，因而只能在有限的时间内从环境中收获有限的熵，所以伪随机数所需的仿真时间少于真随机数。

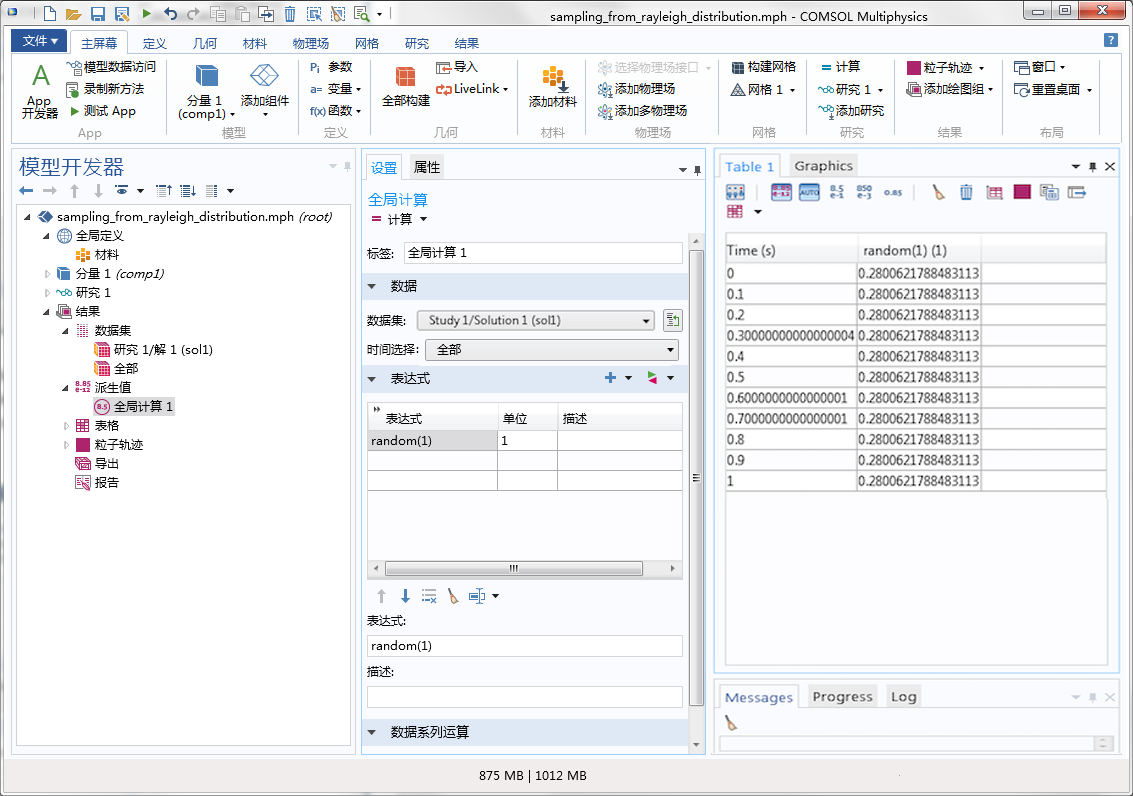
然而伪随机数也存在一些缺点，我们必须采取一些额外的预防措施。种子的数值不同，伪随机数也就不同，但是，相同的种子会反复生成相同的数字。若您想在任意的 COMSOL 模型中验证这一点，可以创建一个“全局计算”节点，并使用恒定种子反复对内置的 random 函数进行计算。现在假设该函数为 random(1)，如下图所示，输出结果与“1”之间不存在明显的关联，因此从这个意义上来说似乎确实是“随机”的；然而若对表达式进行多次计算，得到的值则始终相同，并不会呈现随机分布。

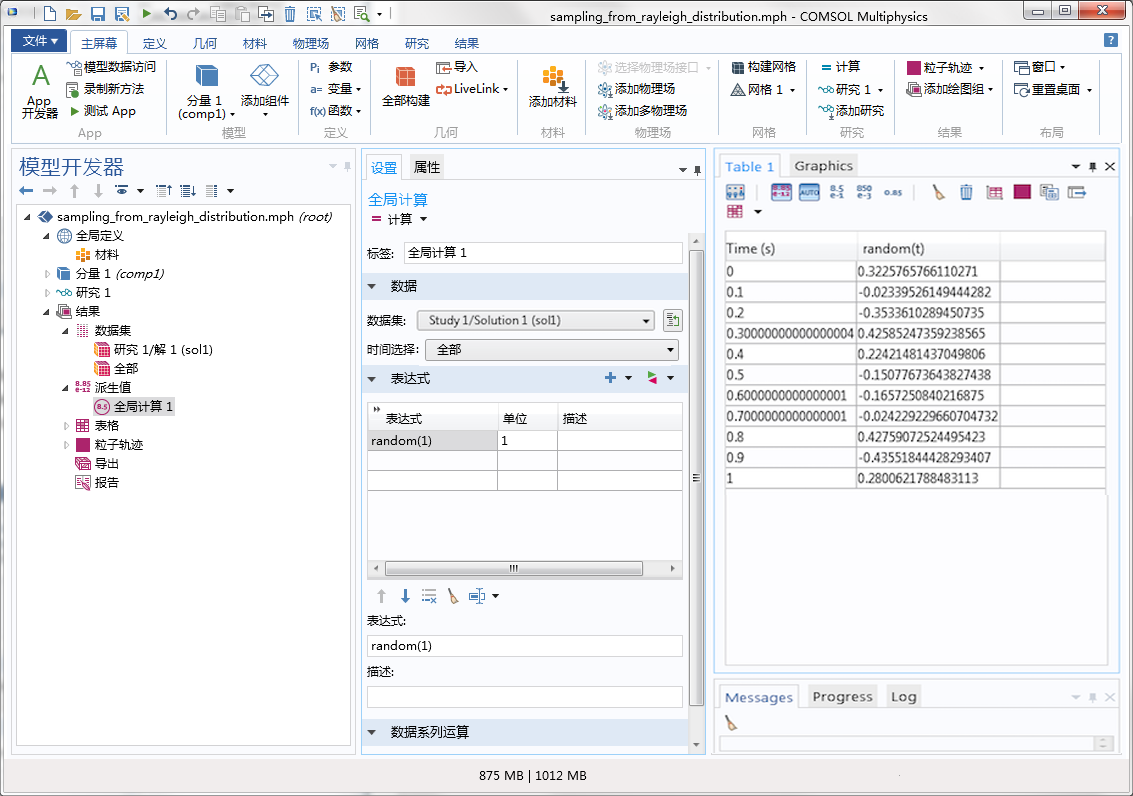
如果在每一次计算随机数时都使用不同的种子，那么每一次都会获得不同的结果。在下方的屏幕截图中，表格中的时间被用作随机函数的输入变元，我们可以将下图的计算结果与上图进行对比。

当模拟粒子系统时，Monte Carlo 仿真往往包含了大量的粒子集群，这些粒子在随机的初始条件下被释放，并受随机力的支配。此类涉及到粒子群随机现象的案例包括：

显然，如果每个粒子得到了完全相同的伪随机数，那么仿真将完全与物理现场相悖。举例来说，就是当离子与背景气体相互作用时，所有离子会在同一时刻与气体分子或原子发生碰撞。为了让粒子是独一无二的，粒子仿真中涉及到的随机数必须具有唯一的种子。

一种方法是将粒子索引 用作种子的一部分，得到的整数与每一个粒子唯一对应。粒子索引变量为 .pidx，其中是物理场接口实例的唯一标识符。在数学粒子追踪 接口中，粒子索引通常为 pt.pidx 。函数 random(pt.pidx) 将为每个粒子分配不同的伪随机数。

若粒子在整个过程中都由随机的力支配，这将产生一个新的问题。举例来说，当使用随机数确定离子是否与气体分子发生碰撞时，您可不希望每一次都为特定粒子分配同一个随机数——否则的话，粒子只能在一个时间步长上发生碰撞或者干脆不碰撞！解决方案是：在随机数种子中引入多个变元，使其至少包含一个与其他粒子不同的变元和一个随仿真时间变化的变元。如果仿真需要对多个伪随机数进行互不干涉的抽样，那么或许需要再添加新变元。随机函数在使用时通常采取 random(pt.pidx,t,1) 的形式，当然，如果确实需要额外的独立伪随机数，我们可以将最终变元 1 替换成其他数字。

Rayleigh 分布的结果

我们来回顾一下最初的 Rayleigh 分布抽样问题。假设我们有一个粒子群，并希望对每个粒子抽样一个数，使结果值符合 Rayleigh 分布。此案例中我们会使用到 σ = 3 的方程（2）。在 COMSOL 模型中定义以下变量：

名称	表达式	描述
`rn`	`0.5+random(pt.pidx)`	`Random argument`
`sigma`	`3`	`Scale parameter`
`val`	`sigmasqrt(-2log(rn))`	`Value sampled from Rayleigh distribution`

请注意，最后一行便是方程（3）。下方的直方图为由 1000 个粒子组成的集群的 rn 值。平滑曲线代表精确 Rayleigh 分布，在这里，我们通过解析函数特征对其进行定义。

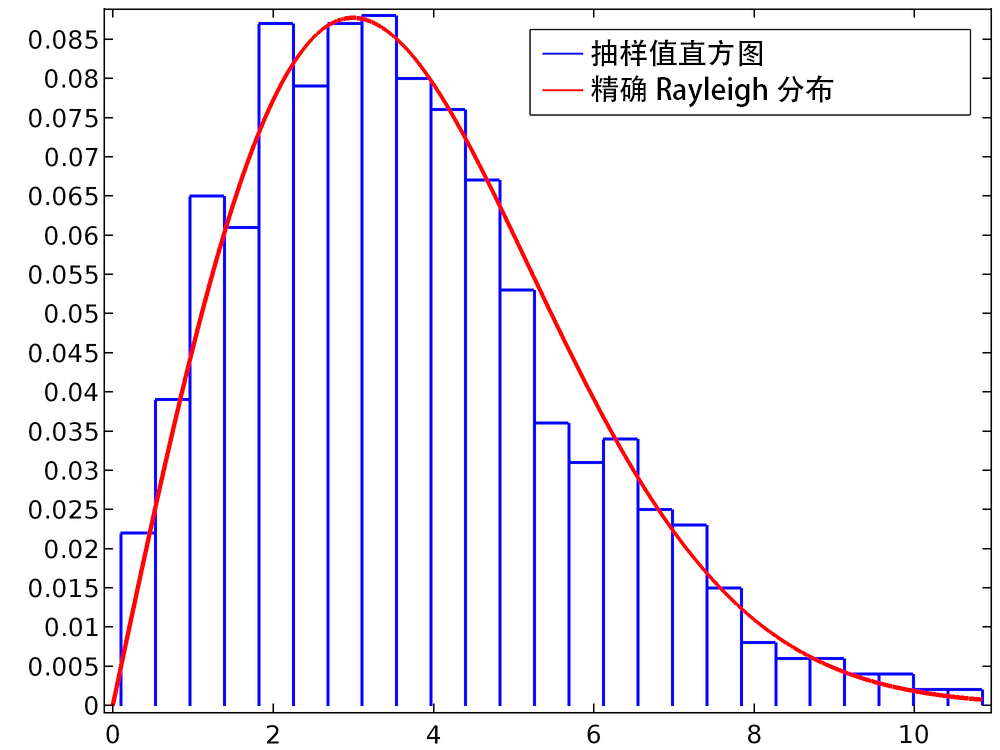
如果您想绘制出包含更丰富信息的精细曲线，那么需要添加更多的粒子来精确地捕获概率分布函数。

插值函数的注意事项

如果将概率分布函数作为插值函数特征，而不是解析或分段函数输入到 COMSOL Multiphysics 中，那么便可通过内置功能自动对随机函数进行定义，此随机函数会从指定的 PDF 中进行抽样。

假设我们的插值函数会对下表中的数据点进行线性插值：

x	f(x)
0	0
0.2	0.6
0.4	0.7
0.6	1.2
0.8	1.2
1	0

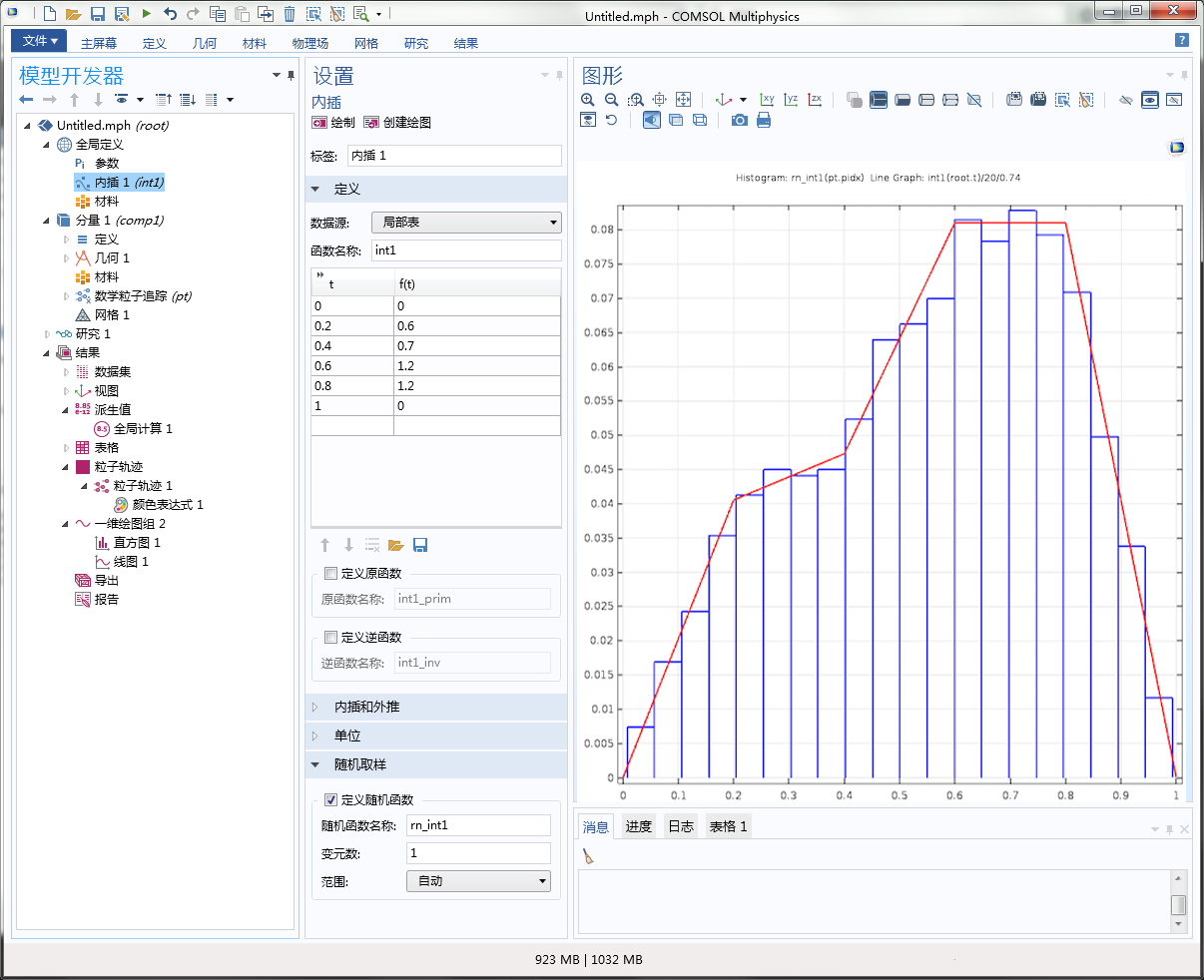
下方的软件截图演示了如何将这些数据输入到“插值”函数中。具体操作方式是打开“插值”函数特征的设置窗口，并勾选定义随机函数 复选框，便能自动对函数 rn_int1 进行定义，此函数可对该分布进行抽样。在“图形”窗口中，直方图显示了 1000 个数据点的随机抽样结果，连续曲线便是插值函数本身。我们还添加了 20 和 0.74 这两个额外的因子，分别用于修正直方图柱条的数目和对插值函数进行归一化处理。

概率分布函数的优势

在本文中，我们解释了概率分布函数、累积分布函数以及与各自逆函数之间的关系。同时还探讨了几种适用于对 COMSOL 模型中的均匀和非均匀概率分布函数进行抽样的技术。在束流物理场中的相空间分布系列的下一篇文章中，我们将对离子束和电子束的物理现象进行阐述，并会阐述为何概率分布函数对于准确模拟束流系统来说是至关重要的。

参考文献

Humphries, Stanley. Charged particle beams. Courier Corporation, 2013.
Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.

]]>