带标签的博客文章 结构力学模块

屈曲,当结构突然坍塌时
解决屈曲问题(如桥梁倒塌或碎苏打罐)的最简单方法是进行线性屈曲分析。在 COMSOL Multiphysics® 中查看如何执行。
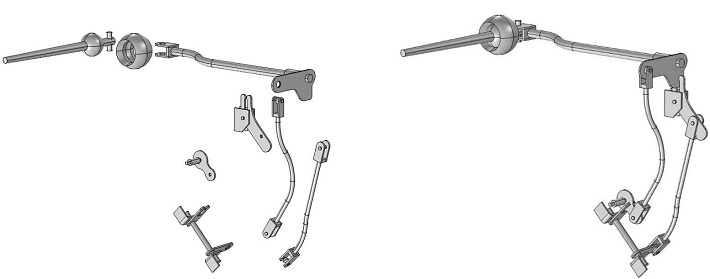
选择第一档:研究老式汽车的换挡原理
跟随我们一起对一辆老爷车的换挡机构进行多体动力学分析。准备上路了吗?

封闭腔体积的求解和控制
在 COMSOL® 软件中,有多种方法可以模拟流体与固体的相互作用。例如,可以使用完整的纳维-斯托克斯方程对压力场和流体速度场进行显式建模。尽管这种方法非常准确,但对于一些流-固耦合问题来说,它的计算成本比实际需要的要高得多。今天这篇文章,我们将介绍一种模拟包含不可压缩流体的封闭腔的方法,假设通过流体的动量和能量传递很小。 编者注: 作者撰写这篇博客的时候,COMSOL 中还没有计算封闭腔中流体载荷的功能。现在,COMSOL Multiphysics® 6.2 版本新增了封闭腔功能,可用于计算封闭腔中的流体载荷。 模拟封闭腔中的流体 我们来看一个 COMSOL 案例库中的示例:超弹性密封条的压缩模型。这个示例考虑的是压缩的软橡胶密封件的横截面。腔体中封闭的流体是空气。该示例计算了压缩力,并将密封件中考虑压缩空气影响与不考虑压缩空气影响的结果进行了比较。 软橡胶密封件的压缩模型。仿真结果显示了应力和应变。使用了不同的方法对密封件内部的空气进行模拟。 示例模型将空气视为可压缩流体,计算了随此二维示例中密封件的横截面积 A 变化的腔体内部压力 p 的变化。接下来,让我们来看看它是如何实现的。将腔体内的空气视为绝热压缩下的理想气体,则压力-密度关系为: \frac{p} {p0}=\left(\frac{\rho} {\rho0} \right)^\gamma=\left(\frac{A0} {A}\right)^\gamma 所以,要计算压力的变化,只需要知道面积的变化就可以了。假设未压缩密封件的面积和压力,以及比热率 \gamma均已知,如何计算横截面积呢?该面积由一个我们甚至不想考虑在模型中的区域来描述。使用高斯定理将面积积分转换为边界积分: A=\int\Omega 1 d\Omega = \int\Omega \left( \nabla \cdot \left[ \begin {array} {c} x \ 0 \end {array} \right]\right) d\Omega = \oint x nx d\Gamma 其中,x 是变形的密封件构型的 x 坐标,n_x 是边界的向外法向量的 x 分量,也在变形配置中,由此给定密封件的封闭区域。这是通过一个定义在封闭体积的完整内部边界上,名为 AreaInt 的积分耦合算子 完成的。变形区域由在“完整模型”上定义的变量 EnclosedArea 定义。 在密封件的内边界上定义面积积分。 分别定义封闭面积和内部压力的变量的定义。必须使用负号来计算面积,因为固体的法线指向腔体。 计算出的变形面积用于确定密封件变形时内部压力的变化。计算得出的压差作为一个载荷施加到密封件内部。要查看上述方法的完整操作,请查看超弹性密封条模型文档。 考虑不可压缩流体 上述方法假设流体是可压缩的,并且密封件的内部压力与面积变化呈函数关系。但如果流体是不可压缩的呢?假设考虑的不是包含可压缩空气的密封件,而是一个充满水的气囊,其中水几乎是不可压缩的。那么,随着结构的变形,封闭的面积不能改变,上述方法就行不通了。因此,我们需要一个替代方案。 我们将 全局方程 功能添加到固体力学接口,通过在这个模型中引入一个额外的方程来求解流体内的压力,使体积不会发生变化。我们来看看这个接口: 引入的全局方程的设置。需要启用高级物理选项才能查看此功能。 上面的屏幕截图显示了用于额外变量 压力 的 全局方程 设置。此方程成立的条件是变量 封闭区域 等于初始面积 123.63 […]

建立子模型:如何分析大型模型中的局部效应
你有没有碰到过对一个具有大量边界条件的特别大的结构进行建模?了解如何使用子模型,这是在COMSOL Multiphysics®中分析大型模型局部效应的一种建模技术。
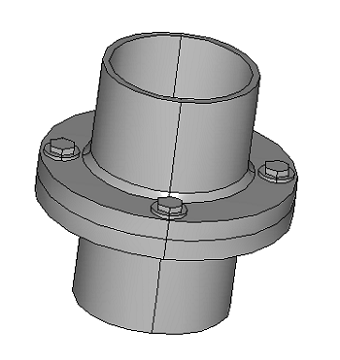
管路连接处预应力螺栓的拉伸应力仿真
在计算拉伸应力之前模拟螺栓预拉伸是一项重要的分析,使用 COMSOL Multiphysics 可轻松进行建模。
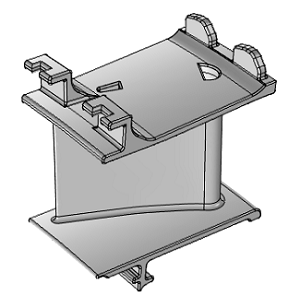
模拟涡轮静叶片的热应力
仿真软件可以帮助我们理解和优化组件设计。任何一个仿真都需要基于实际应用建立模型。建模使我们能够足够详细地表征实际现象,从而获得特定应用或组件的相关信息。
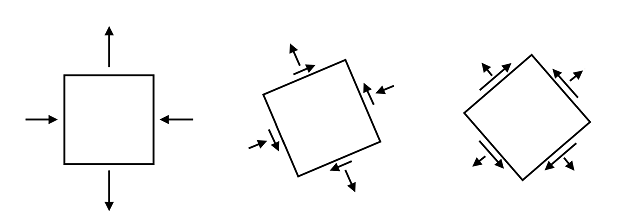
使用临界面法预测疲劳
对疲劳的研究始于 19 世纪,起因是铁路车轴发生故障从而导致了火车事故。在旋转轴中,应力的变化是从拉伸到压缩,再回到拉伸,由于应力状态是单轴和成比例的,因此载荷历程很简单。

使用 COMSOL 模拟离心调速器
无论是小时候坐旋转木马,还是搅拌一桶水并观察水与桶内壁“拥抱”的过程,或是观看泥浆从转动的轮胎上滚落下来,我们可能都见过离心力以这样或那样的方式在发挥作用。
