有意思的弯管应力

对于结构工程师来说，梁理论是一种常用的结构形变分析方法。这些方程使用简单并能提供有用的结果，非常适用于分析结构性能。但是有时候，由于简单和方便，梁理论也会在一些基本假设并不成立的情况下被使用。在这篇文章中，我们将研究这样一个案例，使用梁理论分析这个案例时会存在严重的隐患，从而导致真实的结构性能也存在较大大的差异。

一个思维实验

我们来分析一根由 90° 的弯管和相邻的直管组成的管道，壁厚中等偏薄，如下图所示。假定管道材料为各向同性和线弹性。现在，假设在弯曲平面上弯曲管道，就像图中力的箭头显示的那样。这时，请考虑两个问题：

1. 弯曲的管道将如何变形？
2. 最大的应力会出现在哪里？

一根直管段承受纯弯曲载荷的弯曲管道的横截面。

在边界上施加一个力矩会产生一个变化的表面牵引力。从 COMSOL Multiphysics^®软件 6.1 版本开始，使用边界载荷功能中的合成力载荷类型，就可以轻松施加这种载荷。

你已经有答案了吗？可以在下方的动画视频中查看一个三维实体模型在不同的弯矩作用下的 von Mises 应力和变形。

弯管在不同的弯矩作用下的 von Mises 应力分布和变形。

弯曲力矩变化时，弯管中心截面的 von Mises 应力分布和变形的详细视图。

这个是一根细长的、具有恒定截面的管道，因此在简化分析中，将这种结构作为梁来处理似乎是很自然的选择。弯矩是作用在结构上的唯一载荷，因此对于沿整个梁轴线的任何给定截面来说，它都是恒定的(包括直管和弯管段)。梁理论预测，轴向应力在弯曲平面的最内侧和最外侧达到峰值。但是，实际情况恰恰相反，与梁理论完全相悖！

根据动画显示，von Mises应力分布在管道的顶部和底部达到峰值。最大的应力甚至出现在管道的内部。弯曲的横截面也发生了明显的变形，更具体地说，它呈椭圆形，主轴要么在弯曲平面内，要么垂直于弯曲平面，这取决于弯矩的方向。

用梁理论分析管道

弯管在管道系统中很常见，这些管道通常被用在高压下运输液体或气体。在运输船舶中存在大量的管道，这些管道真令人着迷！

石油或化学品运输船舶上的管道系统。图片经CC BY-SA 3.0授权通过Wikimedia Commons共享。

当涉及到结构分析时，许多用于工业应用的管道标准(或规范)是基于梁理论的。但是，就像我们已经发现的，通常情况下弯管的性能表现与梁不同。仔细研究管道标准，你会发现有很多专门针对管道弯曲的信息。管道标准建议对弯曲管段的刚度和应力采用修正系数(参考文献1)。在简化的项中，来自基本梁理论的弯曲刚度E\,I，应除以一个柔度因子，或K 系数。同样，计算出的应力\sigma，在与允许的应力值比较时，应乘以一个应力增强系数(SIF)，或i 系数。换句话说，普通的梁理论仍然可以应用，但是应该修正弯曲刚度和应力。

管道标准提供了这些校正因子的估计值，这主要取决于管道弯曲的几何形状。在一些情况下，建议使用额外的校正项，来考虑内部和环境压力之间的压力差\Delta p的影响。这是因为内部逾量压强往往会抵抗管道横截面积变形为椭圆，从而产生刚化效果。承受平面内弯曲的弯管的 k 系数和 i 系数的经典定义如下表所示(参考文献2)。

刚度系数	应力校正	柔度特性
校正：E\,I\rightarrow\,\frac{E\,I} {k} k 系数:k = \textrm{max}\left(\frac{1.65}{h}; ~1 \right)	校正:\sigma \rightarrow i \,\sigma i-系数:i = \textrm{max}\left(\frac{0.9}{h^{2/3}}; ~1 \right)	h = \frac{R\textrm{b} t}{r_\textrm{m}^2}

柔度系数h，是一个的无量纲几何量度，它考虑了壁厚t，平均管道半径r_\textrm{m}，和中心线弯曲半径R_\textrm{b}。修正系数的估计值是基于实验数据获得的，或从使用实体或壳体模型的高精度有限元分析中得出。修正系数可以取相当大的数值，这意味着与普通梁理论的偏差是很大的。因此，考虑可能的应力增加和刚度降低以获得保守的结果很关键。下表显示了一系列管道几何形状的校正系数。壁厚t和弯曲半径R_\textrm{b}，与外管半径R_\textrm{o}有关。

几何
\frac{R_\textrm{b}}{R_\textrm{o}}	4	4	4	2	2	2
\frac{t}{R_\textrm{o}}	20%	10%	2%	20%	10%	2%
k	1.7	3.7	20.2	3.3	7.4	40.4
i	1	1.5	4.7	1.4	2.5	7.6

管道标准中提供的修正系数有很长的历史，最早可追溯到 20 世纪 50 年代。虽然这些修正仍在使用，但它们只是唯象模型，不能解释弯管中真正发生的情况。就像上面的应力图中所显示的，弯管的真实行为是一个完整的三维问题。但在进一步研究完整的三维情况之前，我们先来复习一下初等梁理论的一些重要关系。

弯曲的梁

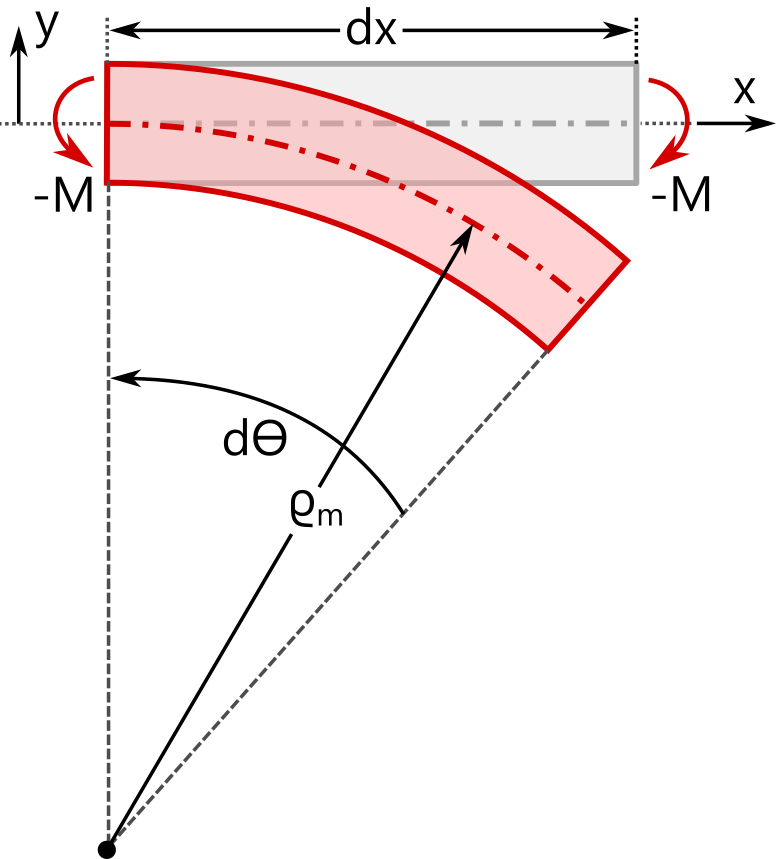
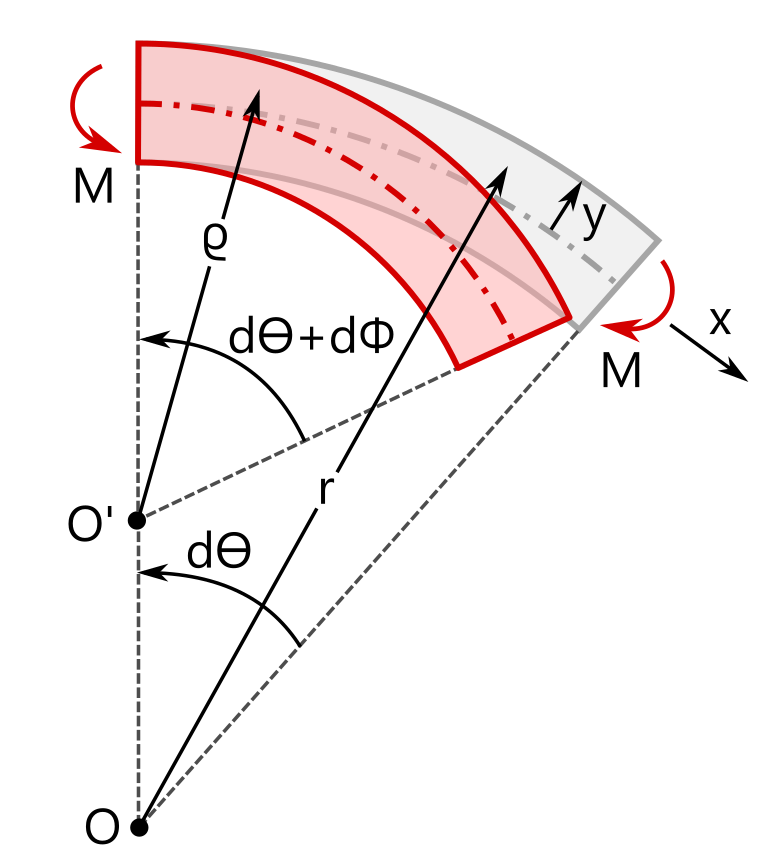
经典梁方程假设梁轴最初是直的，因此，严格来说，这些方程只对直梁有效。如果梁方程是由初始弯曲的梁轴推导出来的，那么与直梁相比，沿轴向的应变定义是不同的，横截面上的轴向应力也不同。下表对初始直梁和初始弯曲梁的假设运动理论进行了比较。未变形的几何形状用灰色显示，变形的几何形状用红色显示。最后一行显示了由外加弯矩M产生的轴向应力的分析表达式。

	直梁	弯曲梁
纯弯曲运动
应变	\varepsilon_{xx} = \frac{(\varrho_\textrm{m} + y) \, \textrm{d} \Theta – \textrm{d}x}{\textrm{d}x}\approx y \frac{\textrm{d} \Theta}{\textrm{d} x}	\varepsilon_{xx}= \frac{\varrho \, (\textrm{d}\Theta + \textrm{d}\Phi) – r \, \textrm{d} \Theta}{r \, \textrm{d} \Theta}
截面惯性矩	I = \int_A \, y^2 \, \textrm{d} \bar{A}	J = \int_A \, \frac{y^2}{1 + y/r_\textrm{c}} \, \textrm{d} \bar{A}
应力	\boxed{\sigma_{xx} (y) = \frac{M}{I} y}	\boxed{\sigma_{xx} (y)= \frac{M}{A \, r_\textrm{c}} + \frac{M}{J} \, \frac{y}{1 + y/r_\textrm{c}}}

在上面表格的表达式中，\sigma_{xx}代表梁的轴向应力。局部坐标y的原点在横截面的质心点。对于弯曲梁，r_\textrm{c}是中心轴的曲率半径。请注意，当半径r_\textrm{c}达到无穷大时，曲梁关系会恢复到直梁关系。

根据直梁的假设，轴向应力在整个截面上线性变化，而在弯曲梁中，应力分布变得非线性，即使假设截面在变形期间保持平面。对于直梁来说，中性轴(\sigma_{xx} = 0)与中心点(y = 0)重合。然而，对于弯曲梁，中性轴和中心点不再重合，请看下面的例子。

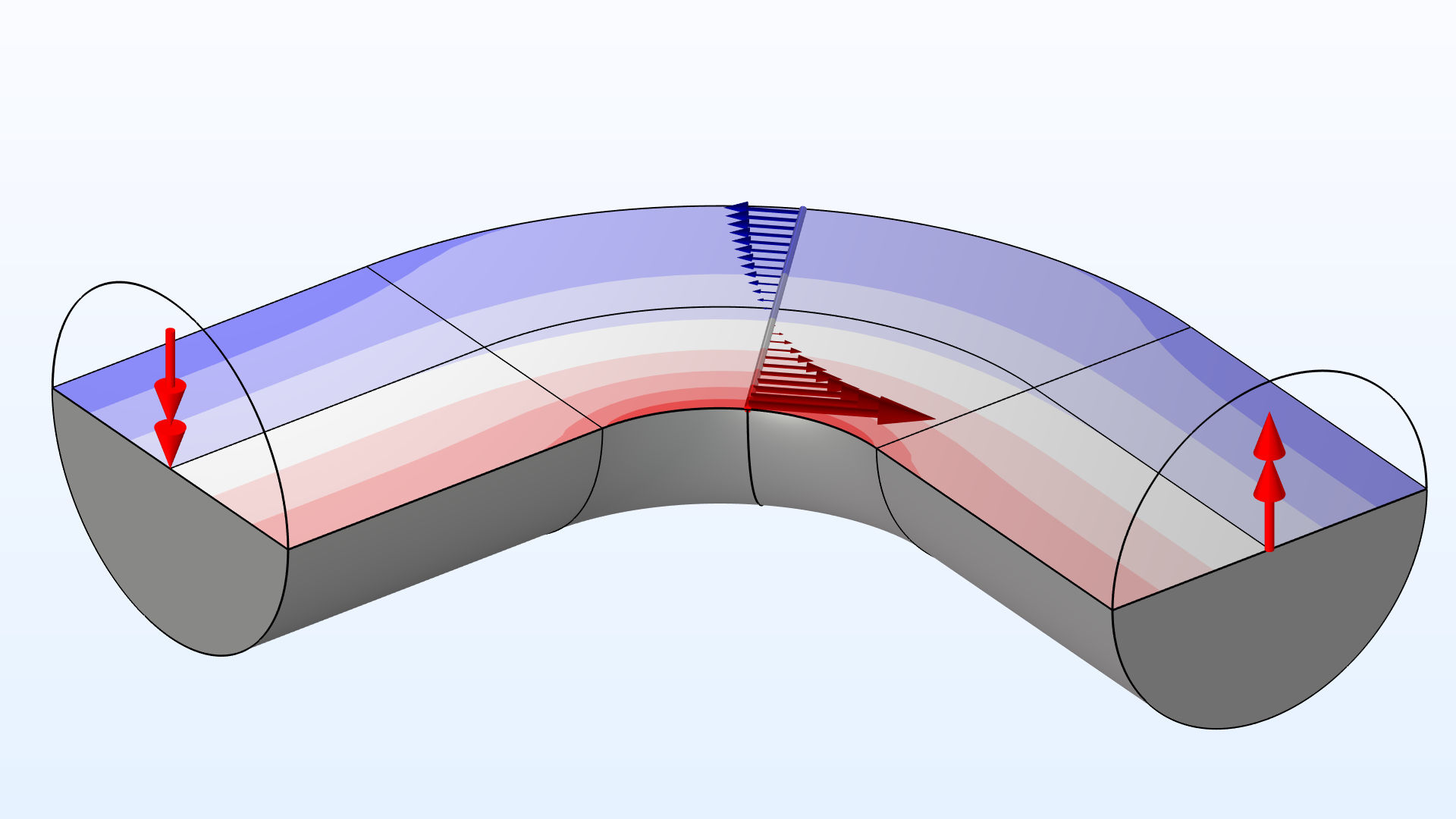
切开一个实心、圆形轮廓的梁。在梁的两端标示了施加的弯矩。由此产生的轴向应力\sigma_{xx}，就像用实体单元计算的那样，在拉伸(红色)和压缩(蓝色)之间变化。在弯曲的部分，\sigma_{xx}有一个非线性的分布。

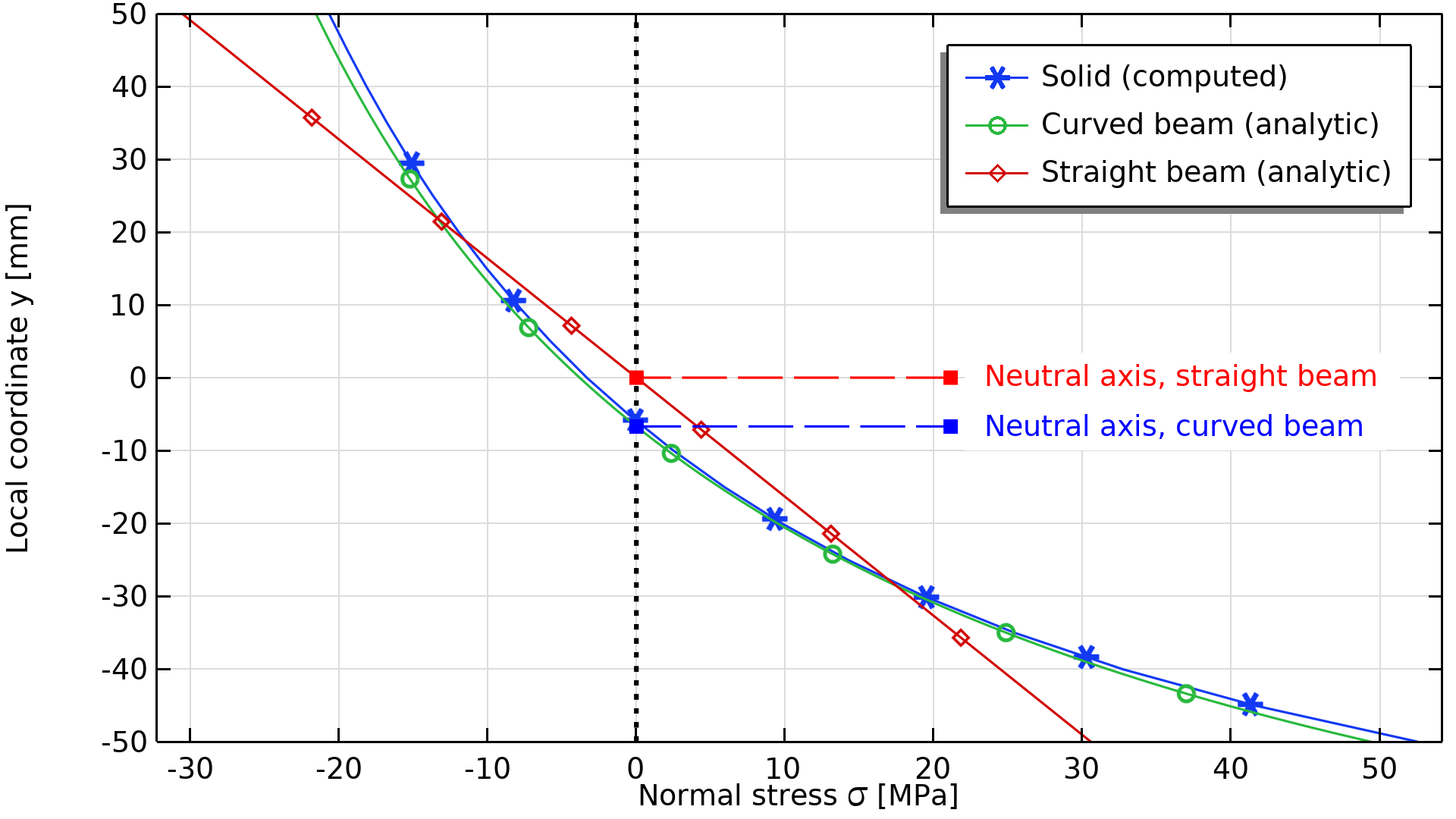
完整的三维实体模型(蓝色)、假设为直梁轴的梁理论(红色)和假设为弯梁轴的梁理论(绿色)计算的轴向应力分布的比较。

即使这个特定的梁绝不是细长的，弯曲梁理论也能与完整的三维实体解匹配。应力比较也强调了直梁理论对高度弯曲的梁的预测结果是不保守的。在这种情况下，最大的应力被低估了大约 40%！然而，对于具有小曲率的梁，使用直梁理论往往还是有用的。有一个经验法则是，当平均曲率半径与梁高之比大于 10 时，经典梁理论通常是可用的。

管道中有什么不同？

我们已经看到用梁理论可以很好地描述实心、圆形截面的弯曲梁。所以一些管道几何形状的行为如此不同的原因一定在于壁厚。和上文一样，下面的动画显示了一个施加了弯曲载荷的 90^°弯管的行为。在这个示例中，弯矩保持不变，而壁厚则减少。

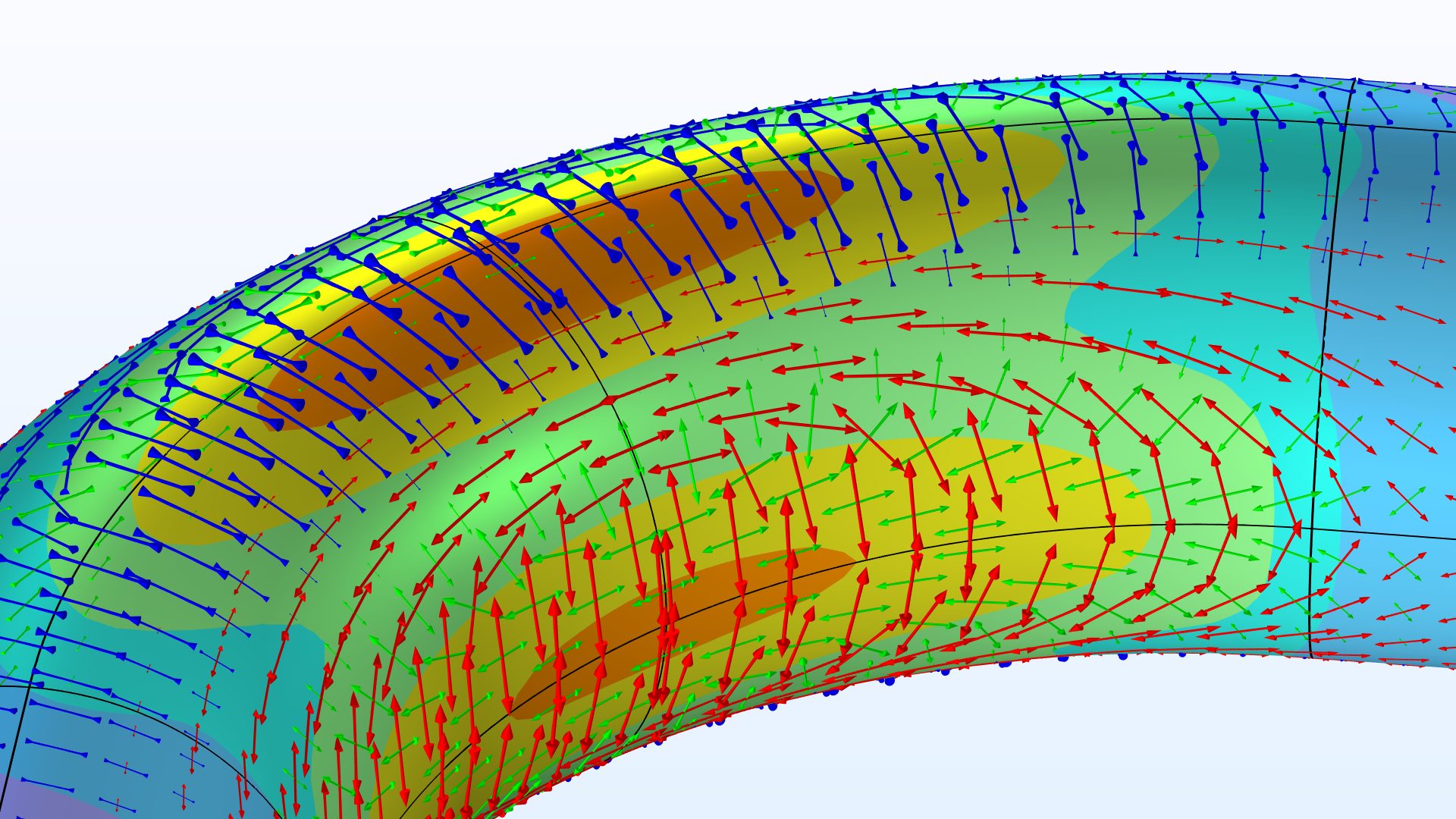
在纯弯曲状态下，不同壁厚的弯管中的 von Mises 应力分布(归一化处理)和主应力。

弯曲管道中心的 von Mises 应力分布(归一化处理)和随壁厚变化的横截面的变形。

对于极厚的管壁(t/R_\textrm{o} > 35\,\%)，管道的行为仍然与梁理论的预测一致。事实上，von Mises应力完全由用于讨论实心梁的应力状态决定，也就是说\sigma_\textrm{mises}\approx | \sigma_{xx} |，\sigma_{xx}
是与梁轴平行的应力。施加的力矩在内半径处引起拉伸应力，并在外半径处引起压缩应力。与直管相比，弯曲部分的应力略高，这一事实也与上面看到的弯曲梁理论完全一致。

\frac{t}{R_\textrm{o}} = 75\,\%	\frac{t}{R_\textrm{o}} = 35\,\%
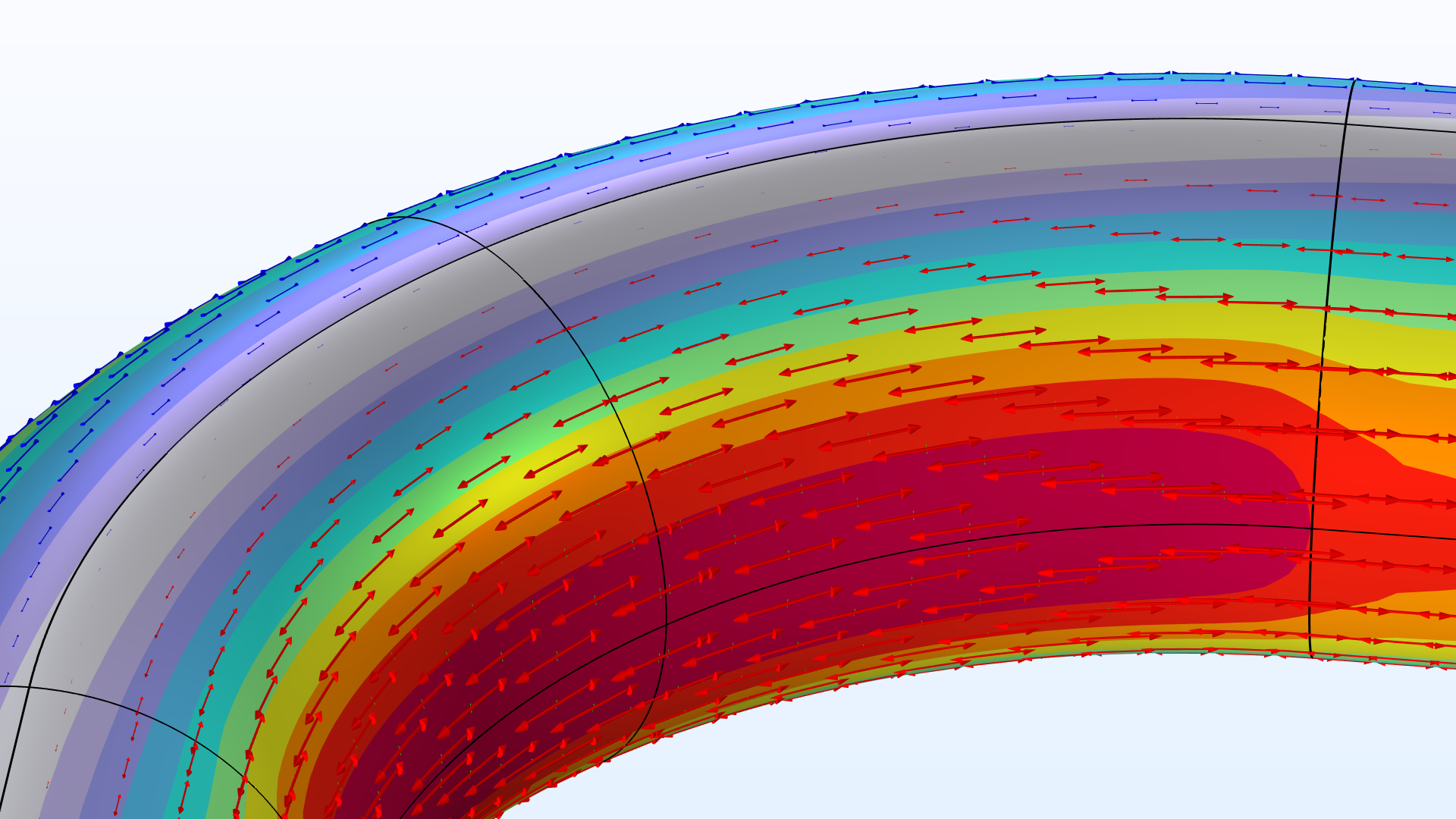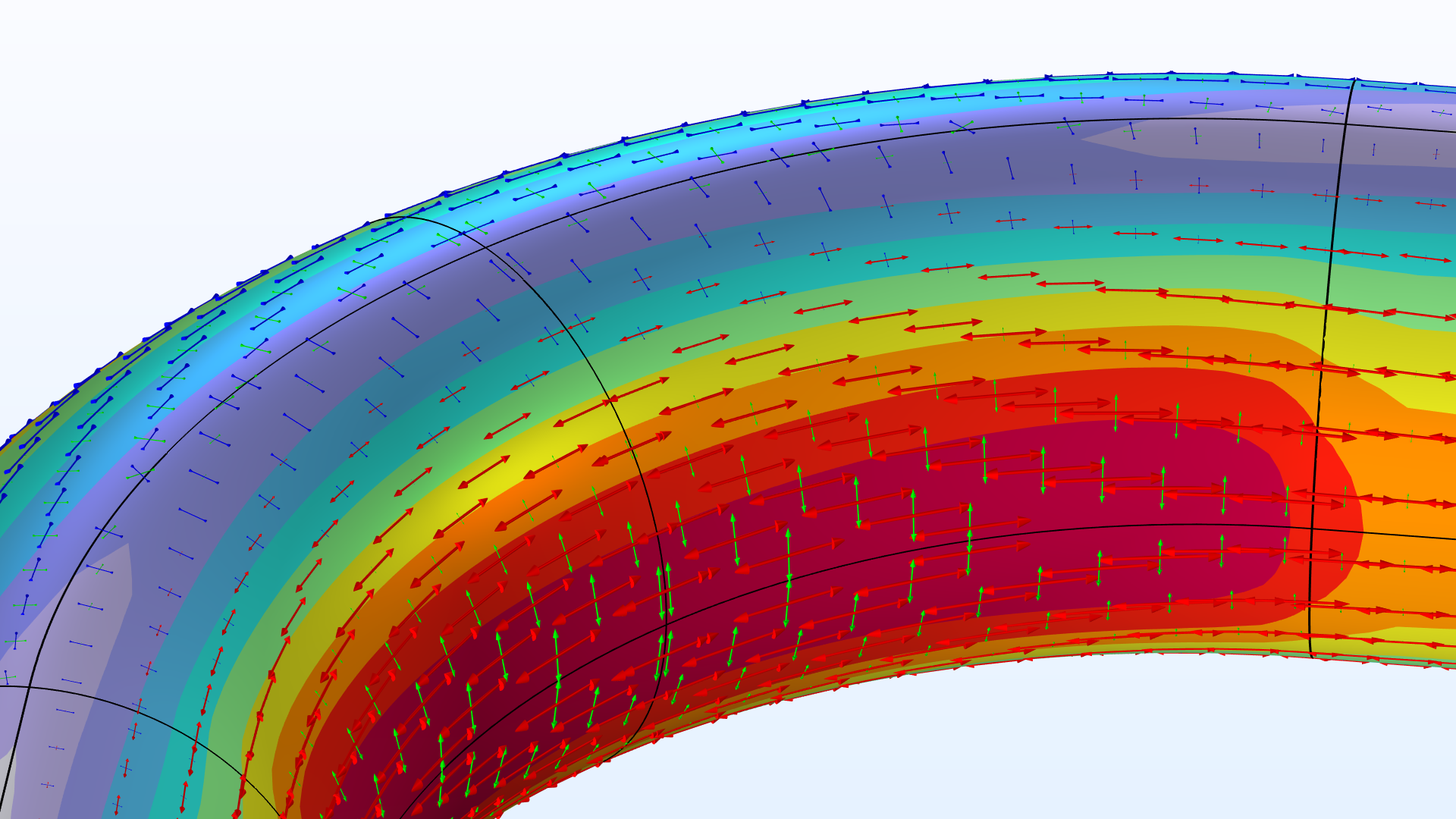\frac{t}{R_\textrm{o}} = 20\,\%	\frac{t}{R_\textrm{o}} = 10\,\%
\frac{t}{R_\textrm{o}} = 5\,\%	\frac{t}{R_\textrm{o}} = 2.5\,\%

弯管视图显示了不同壁厚的 von Mises 应力(归一化处理)和主应力。

相对于较厚t/R_\textrm{o}\approx 35\,\%(对于任何实际应用来说，这其实是非常厚的)的管壁，应力分布开始发生非常大的变化。额外的垂直拉伸应力在内弯半径和外弯半径处叠加了梁的解，同时，管道的顶部和底部显示出压缩应力，这些额外的周向应力是由于横截面逐渐变得椭圆而产生的。普通梁理论明确地忽略了这种横截面的变形，而且在描述其影响方面确实存在不足。

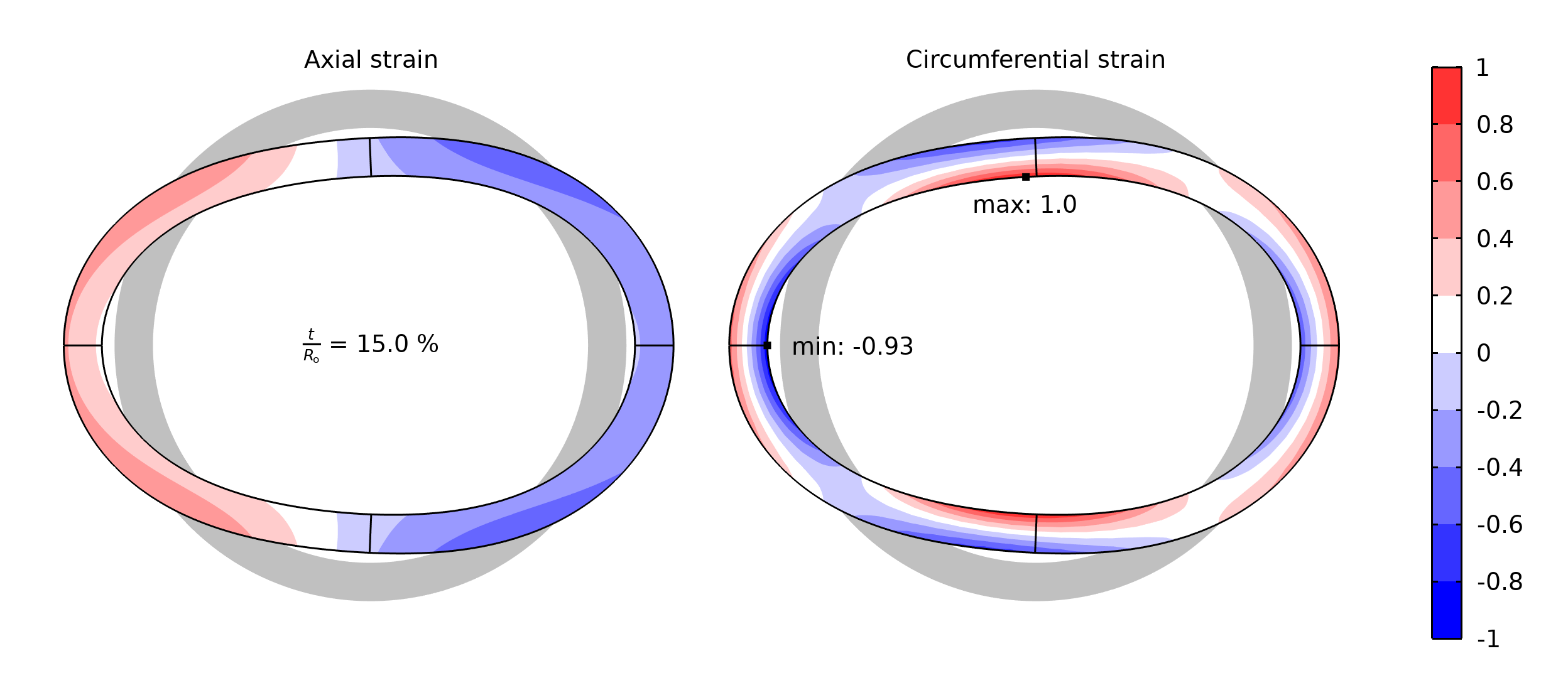
厚壁弯管中心的轴向和圆周方向的归一化应变的比较。椭圆化(高度夸张的)导致周向应变的峰值高于轴向应变。

壁厚较小产生了更加明显的椭圆形，这种对初始圆形轮廓的偏离在顶部和底部最极端。横截面的变形可以被看作局部的 “弯曲变形”，在管壁的圆周方向引起应变。在内壁半径处，局部变形与较小的初始弧长相比，应变(以及由此产生的应力)达到最高值。

在 COMSOL 中建立管道模型

COMSOL Multiphysics^®软件内置了很多功能可以分析具有不同精度水平的管道。让我们来看一些例子。

管道力学接口

管道力学接口是梁接口的一个特殊版本。增强的功能使这个接口能够考虑到流体属性，并轻松设置多物理场耦合，以包括流体和热效应。

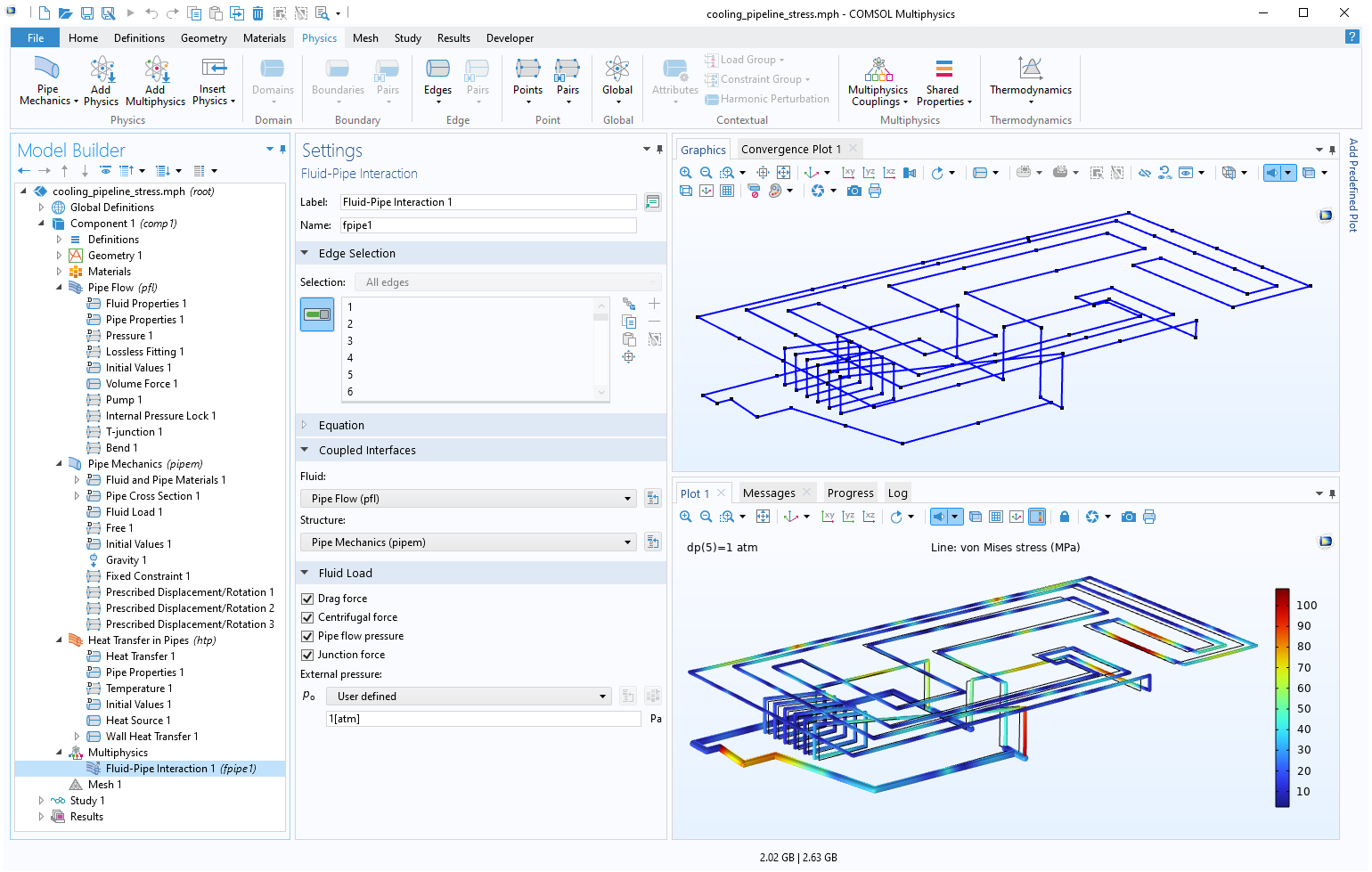
一个耦合了结构、流体和热效应的管道力学模型

管道力学接口也有一个内置的弯头功能，通过提供 K 系数和 SIF 来校正刚度和应力。

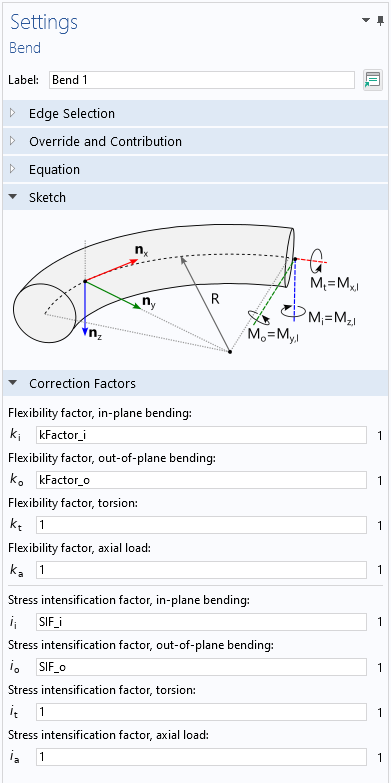
弯头功能的设置窗口，显示了刚度和应力修正系数。

子模型部件

虽然管道系统的大型部件通常可以用梁理论很好地近似，但有些部件可能更适合用实体或壳单元进行高精度建模。对于这种情况，在位移和旋转自由度(DOFs)之间建立正确的运动学耦合是很重要的。使用结构-管连接多物理场耦合，就可以很容易地添加一致性的耦合。

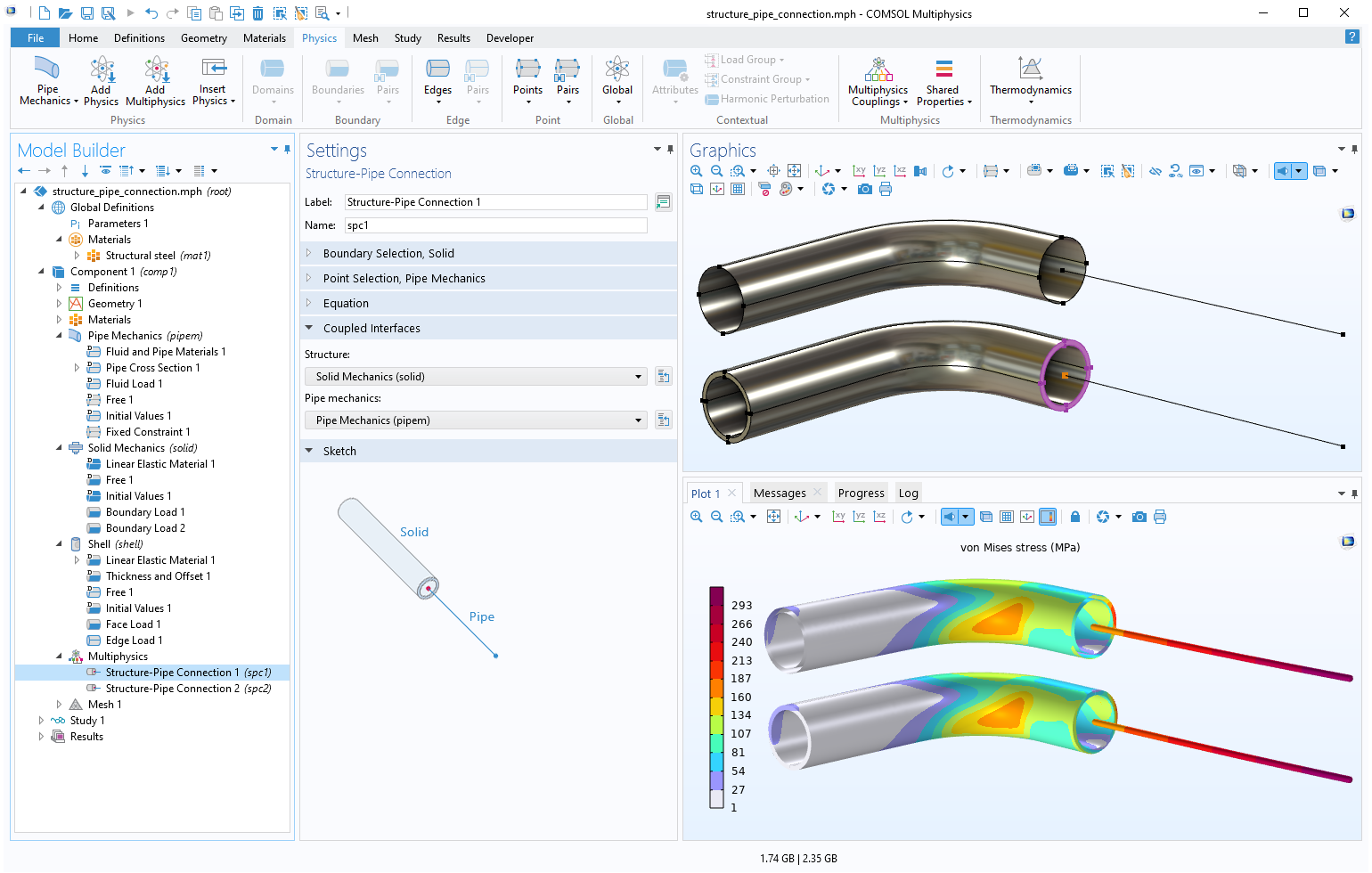
使用结构-管连接多物理场耦合，将管道力学接口与固体力学或壳接口耦合。

几何零件

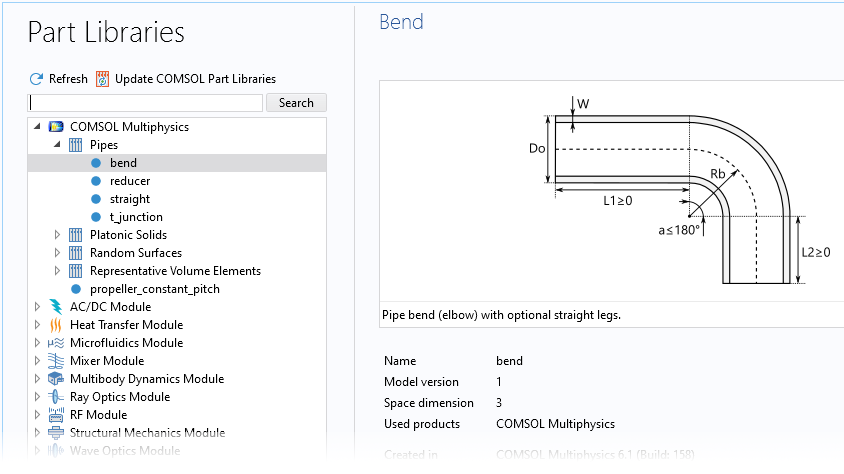
COMSOL Multiphysics 还为三维管道分析提供了许多预定义的几何零件，用于结构和流体分析。这些内置的、完全参数化的零件可以在 COMSOL 零件库中找到。这些零件经过优化，可以方便地进行网格划分，其中包含有用的预定义选择和工作平面，可以轻松地连接部件和建立复杂的管道系统。

COMSOL 零件库(左)提供了许多内置的几何零件，例如完全参数化的管道零件。右图是一个由内置几何零件创建的管道系统的例子。

扩展阅读

阅读下列 COMSOL 博客文章，了解更多有关建模和仿真在管道设计中的应用。

• 利用拓扑优化设计区域热网
• 地下管道应力腐蚀的多物理场模拟
• 利用色散曲线分析充液管道
• 根据 CAD 装配分析螺纹管件设计中的应力

参考文献

1. E.A. Wais and E.C. Rodabaugh, “Background of SIFs and Stress Indices for Moment Loadings of Piping Components”, United States, 2005;https://www.osti.gov/biblio/841246
2. “Stress Intensification Factors (i-Factors), Flexibility Factors (k-Factors), and Their Determination for Metallic Piping Components,” ASME, 2017;https://www.asme.org/codes-standards/find-codes-standards/b31j-stress-intensification-factors-flexibility-factors-determination-metallic-piping-components/2017/drm-enabled-pdf