具有滞后的相变材料的热建模

今天的博客，我们将介绍一种对热滞材料进行建模的程序，这意味着熔化温度与凝固温度不同。这种行为可以通过引入与温度相关的比热函数来建模，如果材料被加热或冷却超过某个点，该比热函数会有所不同。我们可以在 COMSOL Multiphysics 中通过上一个解运算符和一些基于方程的建模来实现这种行为。让我们来看看如何操作……

什么是热滞，如何模拟？

热滞材料的凝固温度将表现出与熔化温度不同。这种材料被应用在散热器和蓄热系统中，甚至被生物体使用，例如生活在寒冷气候中的鱼类和昆虫。在这篇文章中，我们不会关注热滞的确切物理机理，而是关注如何对它进行建模。

首先考虑一种具有不可压缩滞回的代表性材料，并将材料的焓绘制为温度的函数，如下图所示。当材料处于固态并被加热时，焓由底部曲线或路径给出。当材料通过熔化温度时，它变成完全液态。当该材料随后以液态冷却时，它将遵循上部路径，因此材料在低于熔化温度的温度下保持液态。一旦达到冻结温度，材料就会变成完全固体。如果材料随后被加热回去，它将沿着底部路径，依此类推。在完全熔化或完全固态下，两条焓曲线重叠。这些曲线中的跳跃是熔化和凝固的潜热。

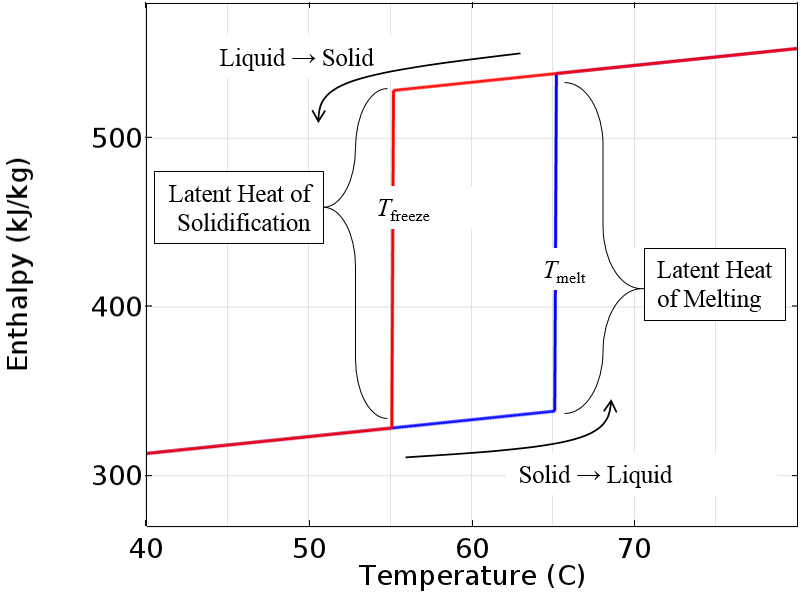
理想的不可压缩材料的焓与温度的关系。

现在，上面的曲线代表了一个理想的情况，只有在材料完全纯净时，这个曲线才会发生在真实世界中。对于计算建模来说，这也有点不切实际，因为状态之间的这种即时转换表示了一种很难用数值解决的不连续性。

然而，如果我们引入一个小的过渡区域，使焓在其上平滑变化，那么我们就会得到一个更适合数值分析的模型。对此的物理解释是，材料在某个有限的温度下发生相改变，在中间范围内，材料是固体和液体的混合物。只有当材料完全超出过渡区域时，它才会切换到遵循另一条曲线路径。

请注意，我们将平滑集中在标称熔化和冻结温度周围，因此完全熔融状态的温度略高于标称熔化温度，而完全固态的温度略低于冻结温度。下图显示了逐渐平滑，但是如果我们确实拥有完全纯净的材料，那么可以使这个过渡区域非常狭窄，以更好地近似理想行为。

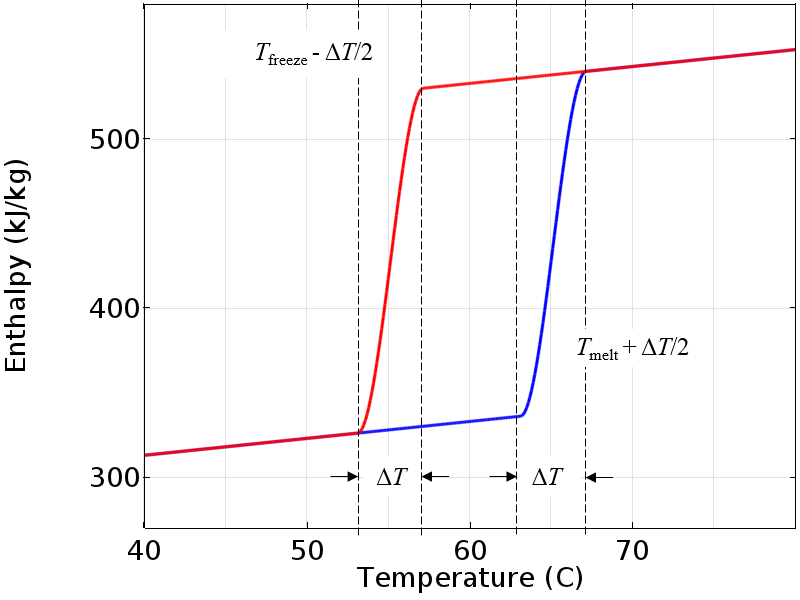
平滑的焓曲线更适合进行数值分析。

由于假定材料是不可压缩的，因此焓仅取决于温度。上面的图还将为我们提供比热，即焓相对于温度的导数。比热是恒定的，除了熔化和冻结温度周围的一小块区域。

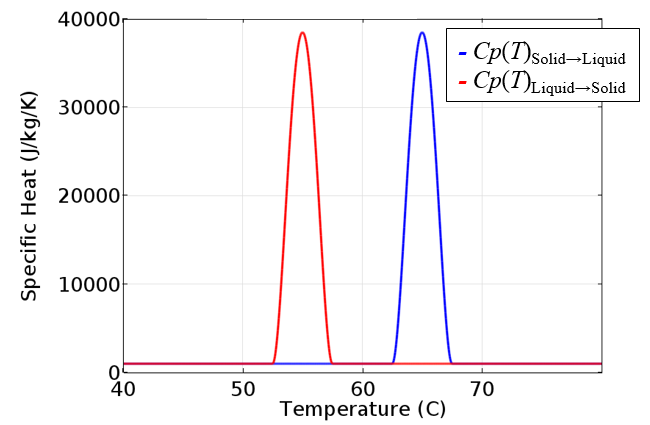
比热是焓相对于温度的导数，如果材料被加热或冷却，则比热是不同的。

这些与温度相关的比热数据可以直接放入传热控制方程中，并结合一组适当的边界条件，在 COMSOL Multiphysics 中求解。事实上，现有的案例库中的示例“金属冷却和凝固”案例模型利用了这种与温度相关的比热，尽管没有滞回。对热滞进行建模的唯一附加要求是引入一个开关来确定要遵循的路径。现在，我们来看看如何在 COMSOL Multiphysics 中实现这一点。

在 COMSOL Multiphysics 中实现热滞建模

我们将以一个薄壁容器内相变材料的简单模型为例来说明。在该模型中，一侧壁是完全绝缘的，另一侧壁维持一个已知的温度，该温度随时间周期性变化。如下图所示。我们感兴趣的是通过厚度计算温度作为时间和位置的函数，并且可以将其简化为一维模型开始使用。

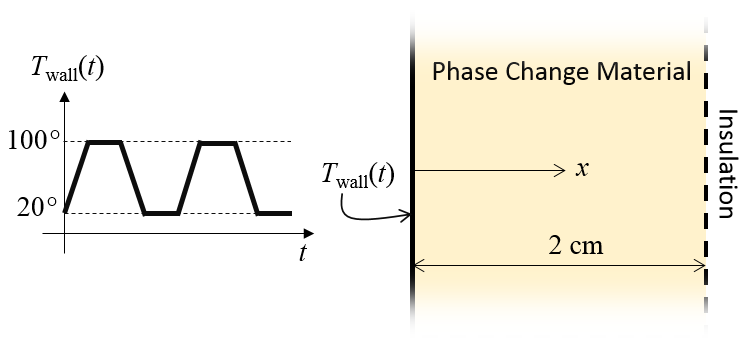
热模拟的示意图。在一侧施加随时间变化的温度。

我们的建模首先通过全局参数设置一些物理常数，这些参数定义了熔化和冻结温度以及应用于焓函数的平滑。下面的屏幕截图显示，实现了前面绘制的两个平滑焓函数。我们可以在这里利用内置的Step函数，该函数还具有应用用户定义的平滑的选项。

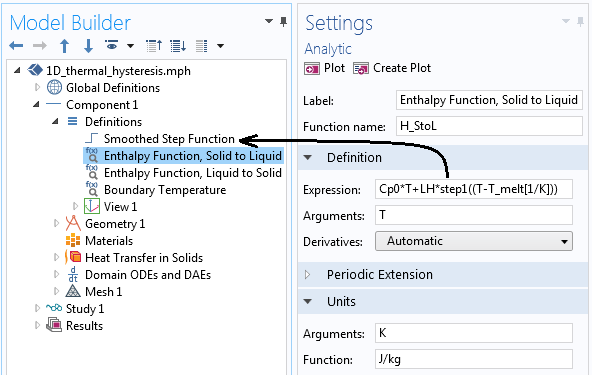
使用平滑阶跃函数实现上面显示的焓函数。请注意，单位已定义。

我们模型的几何形状只是一个表示相变材料区域的一维间隔。使用固体传热接口，因为我们假设没有流体流动。材料属性如下所示。

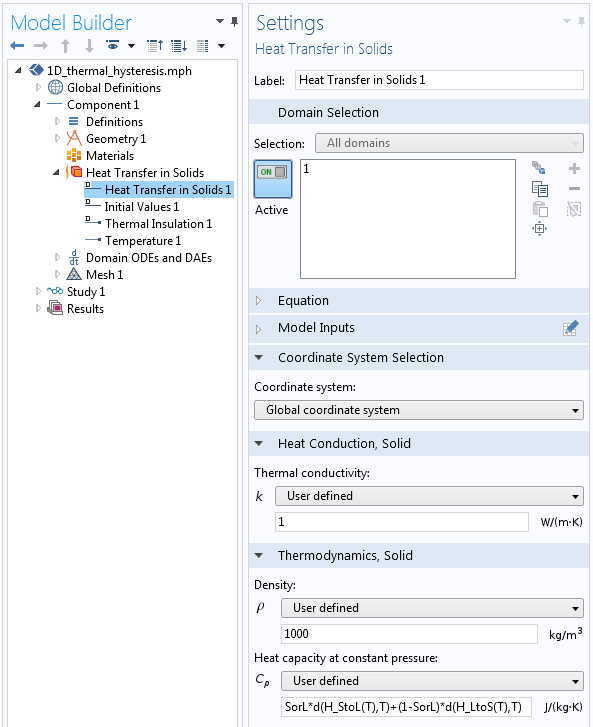
显示相变材料中的材料属性定义的屏幕截图。

导热系数和密度是常数。比热（恒压下的热容）的定义如下：

SorL*d(H_StoL(T),T)+(1-SorL)*d(H_LtoS(T),T)

其中微分算子取两个不同焓函数相对于温度的导数，SorL变量将局部材料行为定义为固体或液体。变量SorL可以是 0 或 1，并且每个单元中可以不同。

域常微分方程和微分代数方程接口用于定义这个变量，接口设置如下图所示。请注意，因变量和源项都是无量纲的，形状函数的类型为间断拉格朗日—常数，这意味着变量SorL将在每个单元中采用不同的常量值。

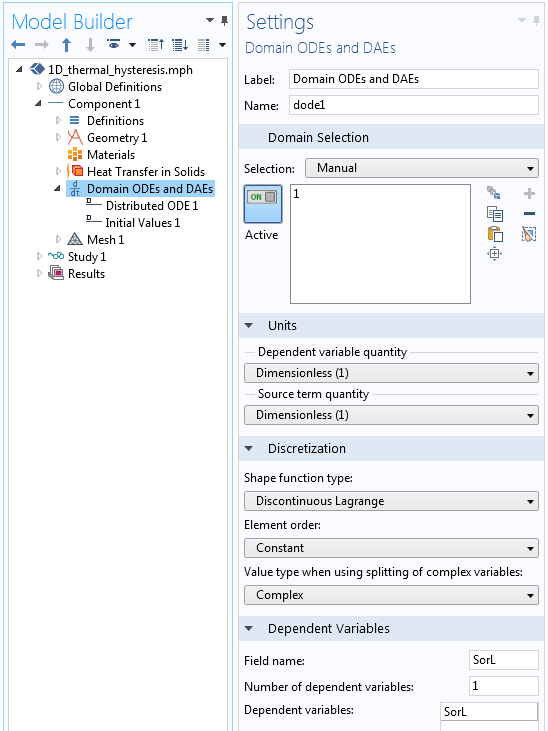
跟踪材料状态的域常微分方程和微分代数方程接口的设置。

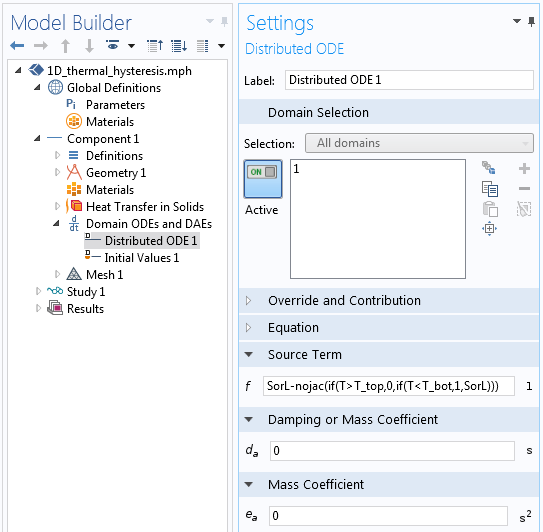
源项设置。

上面的屏幕截图描述了在域常微分方程和微分代数方程接口中求解的公式。我们来详细查看使用的源项方程：

SorL-nojac(if(T> T_top,0,if(T< T_bot,1,SorL)))

该方程在每个单元的质心处计算，并在一行中实现以下内容：

如果当前温度大于完全熔化的温度（标称熔化温度加上平滑温度的一半），那么材料已通过其固液相变温度，设定SorL = 0。这意味着遵循液体到固体的焓曲线。如果当前温度低于完全凝固的温度（标称冻结温度减去平滑温度的一半），那么材料已经过了其液固相变温度，设定SorL = 1。这意味着遵循固液焓曲线。否则，当前两个条件都不满足时，将SorL变量保留在其先前的值，这意味着在中间区域中没有路径更改。

nojac()运算符告诉软件从雅可比计算中排除封闭表达式，因此它不会尝试区分封闭表达式，而只是在每个时间步长计算表达式本身。

如前所述，使用SorL变量定义在模型相变材料域的比热。适当地设置变量的初始值也很重要。如果相变材料的初始温度高于或低于完全熔化或凝固的温度，那么这个选择是明确的;否则，必须选择材质的初始状态。在这里的示例中，我们将考虑系统的初始温度低于冻结温度，因此材料最初将遵循固液路径。因此，变量SorL的初始值设置为 1。

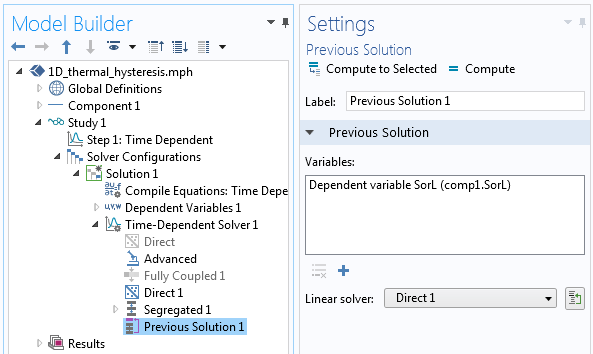
显示了上一个解运算符。

在求解模型方面，我们只需要记住，变量SorL需要在求解器序列中使用上一个解运算符在上一个时间步长进行计算，如上面的屏幕截图所示。我们也可以使用分离式求解器，当然，我们应该研究收紧瞬态求解器公差、因变量的缩放，并通过网格细化研究解的收敛性。

现在让我们看一些结果。在下面的图中，我们看到了相变材料加热和冷却的建模域厚度的温度。我们可以观察到温度的斜率作为位置的函数随着材料通过熔点和冰点而变化。这是由于在材料变化阶段时必须添加或去除额外的热量。

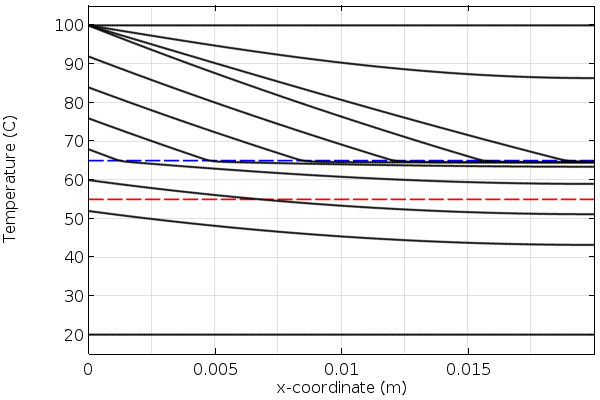
加热过程中相变材料的温度随时间变化。蓝线是熔化温度。

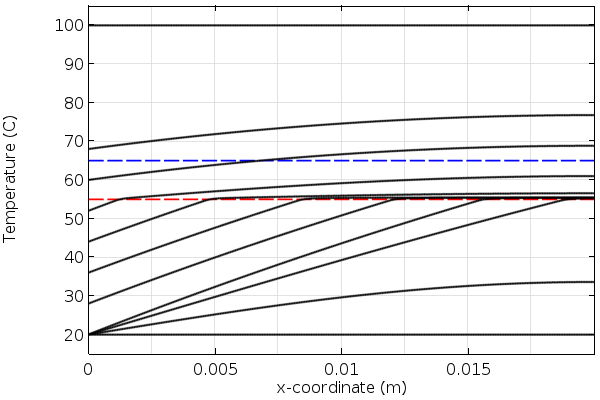
冷却过程中材料中的温度随时间变化。红线是冻结温度。

显示加热和冷却期间随时间变化的组合温度曲线的动画。蓝线和红线是融化和冻结温度。

关于模拟热滞材料的结束语

今天，我们介绍了一种在假设密度恒定的条件下，模拟热滞材料的方法，并且材料必须完全高于和低于熔化和冻结温度才能改变相位。这个建模方法利用了上一个解运算符和基于方程的建模。有关上一个解运算符的用法和更多示例请参阅以下博客：

• 在瞬态模拟中使用上一个解运算符
• 使用上一个解运算符追踪材料损坏

为了便于解释，这里显示的方法略有简化。如果您对具有相变的传热建模感兴趣，无论是否具有热滞，我们建议您查看传热模块，该模块具有用于模拟相变传热的内置接口，点击此处查看。

如果您对不可逆相变建模感兴趣，那么您可以再了解一下我们之前关于模拟热固化过程，以及使用上一个解运算符追踪材料损坏的博客文章。

如果您想自己动手在 COMSOL Multiphysics 中对热滞进行建模，或者对此过程有其他疑问？请联系我们。