基于密度-梯度理论建立的三种半导体器件模型

在上一篇博文中，我们简要介绍了密度梯度理论（参考文献1），该理论考虑了传统漂移-扩散方程中量子约束的影响，且不需要过多的额外计算成本。因此，与其他更复杂的量子力学方法相比，这个理论可以加快工程研究的速度。今天这篇文章，我们将继续介绍几个例子来展示这种建模方法在半导体器件仿真中的优势。

案例 1:硅反型层

金属氧化物硅（MOS）结构是许多硅平面器件的基本构建单元。已有使用各种技术对氧化硅界面下的反型层进行了大量的研究。案例 1 使用了传统的漂移-扩散方程、密度梯度理论和全量子力学薛定谔-泊松方程，对参考文献2中的硅反型层进行了仿真。栅极氧化物的厚度为 3.1 nm，掺杂浓度为 3.8e16 1/cm³。密度梯度的有效质量是电子质量的 1/3。温度为 300 K，采用费米-狄拉克统计。

如下图所示，由漂移-扩散方程计算所得的电子浓度分布（标记为“DD”）明显缺乏量子约束的影响，而由密度梯度公式计算得到的电子浓度分布（标记为“DG”）则非常接近使用薛定谔-泊松方程计算得到的电子浓度分布（标记为“SP”）。

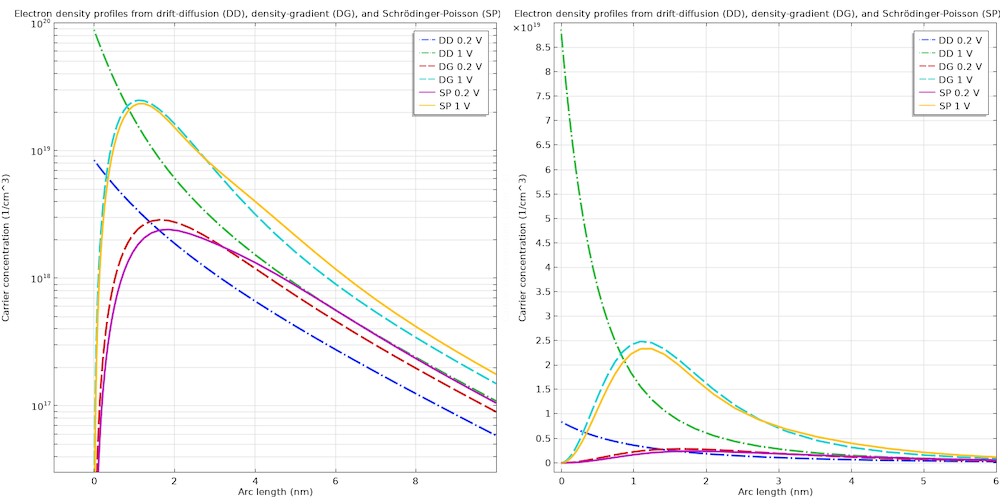
使用传统的漂移-扩散公式（DD）、密度梯度理论（DG）和薛定谔-泊松方程（SP）计算的电子密度曲线。左：对数比例，右：线性比例。

虽然使用密度梯度理论计算的结果与完全量子力学计算的结果并不完全一致，但比使用传统的漂移-扩散公式有了巨大的改进。此外，它比使用薛定谔-泊松方程需要的计算资源要少得多。在这个简单的一维模型中，密度梯度的计算时间为 6 秒，而使用薛定谔-泊松方程的计算时间为 253 秒。在更高维度的更复杂的模型中，这一差异将变得更大。

案例 2:纳米线金属氧化物半导体场效应晶体管

案例 2 的硅纳米线金属氧化物半导体场效应晶体管（MOSFET）的三维模型是基于参考文献3建立的。模拟结构的沟道是由一个矩形硅纳米线形成的，其截面是一个 3.2 nm 的正方形，周围是厚度为 0.8 nm 的氧化层。该通道的长度为 4 nm，温度保持在 300 K。文献中使用了麦克斯韦-波尔兹曼统计。

在这个模型中，密度-梯度有效质量呈各向异性。在 COMSOL 中，我们可以通过在材料属性中选择对角线，在设置窗口选择密度-梯度来实现半导体材料模拟域条件，如下面的截图所示。

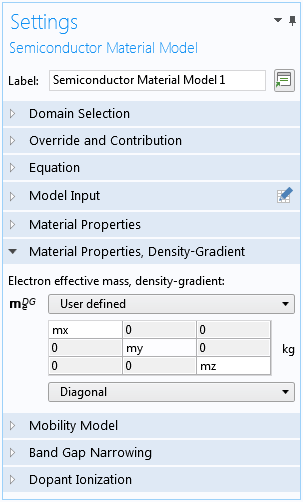
各向异性有效质量矩阵的设置。

在 COMSOL 中，使用电荷守恒 域条件明确模拟氧化物层。选择绝缘体界面 边界条件的势垒选项实现硅-氧化物界面的量子约束效应，如下面的截图所示。这个选项实现了文献4中描述的边界条件，这在上一篇博客文章中作过简要讨论，感兴趣读者的可以阅读。

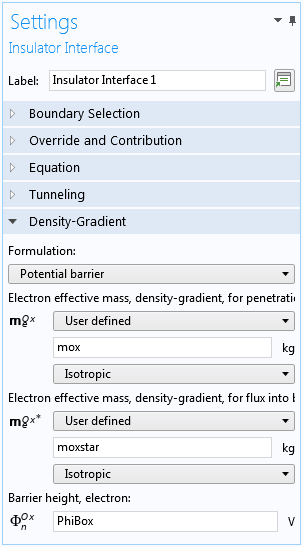
在半导体-绝缘体界面添加量子约束的设置。

下图中显示的 I-V 曲线和电子密度分布都与参考文献3中的相应绘图结果一致。

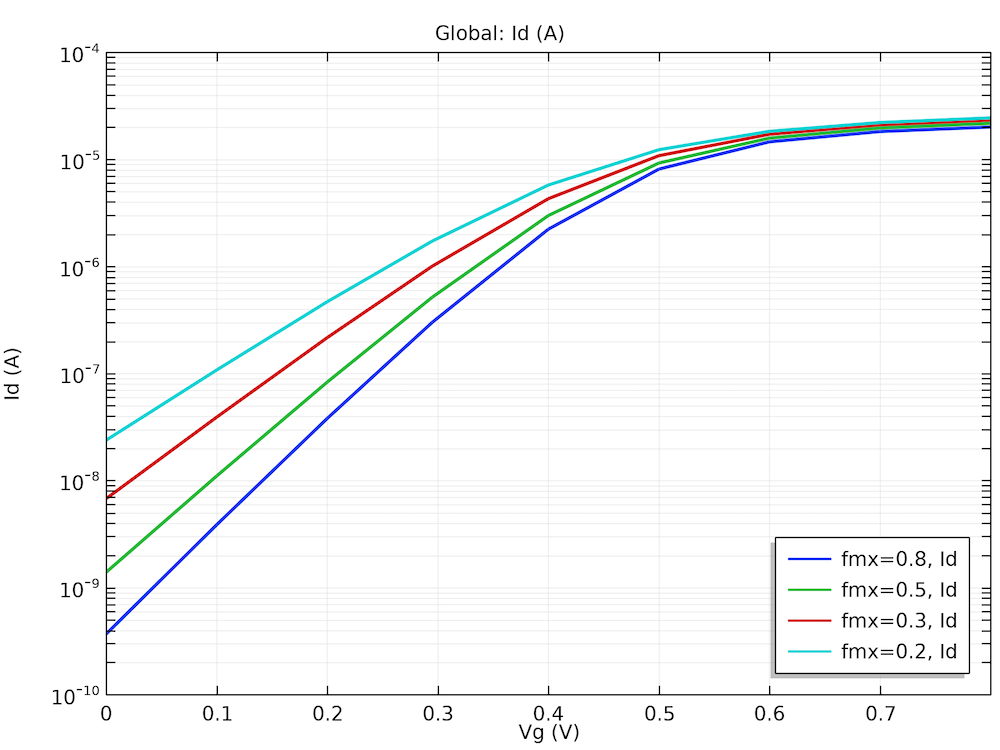
一组密度梯度的纵向有效质量的 I-V 曲线。

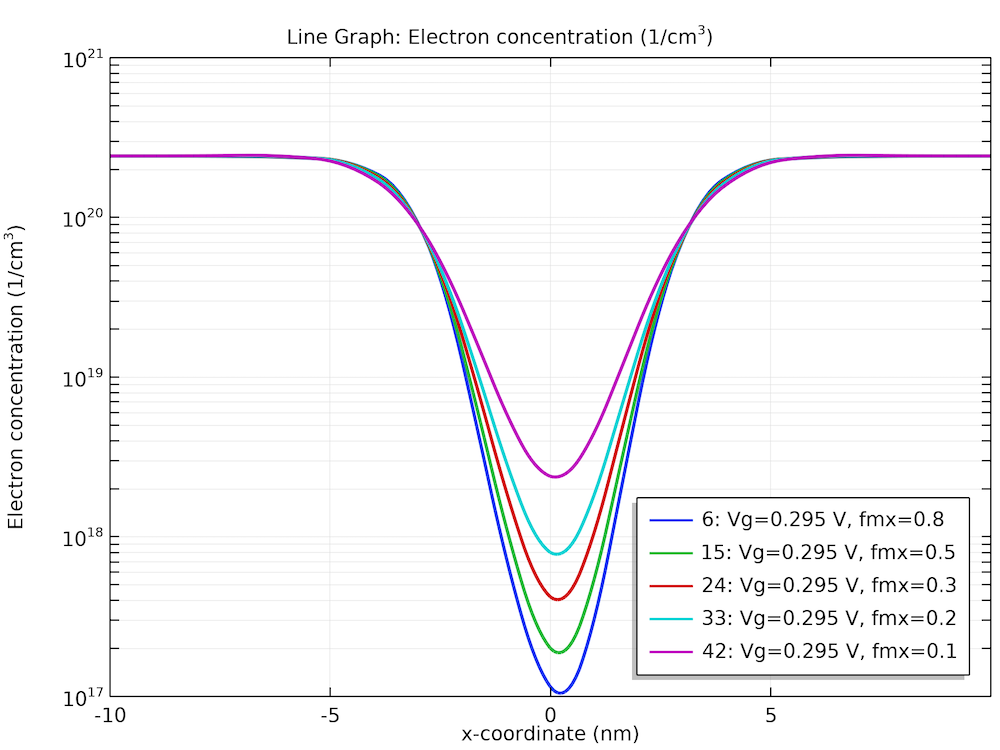
一组密度梯度纵向有效质量的纵向电子浓度曲线。

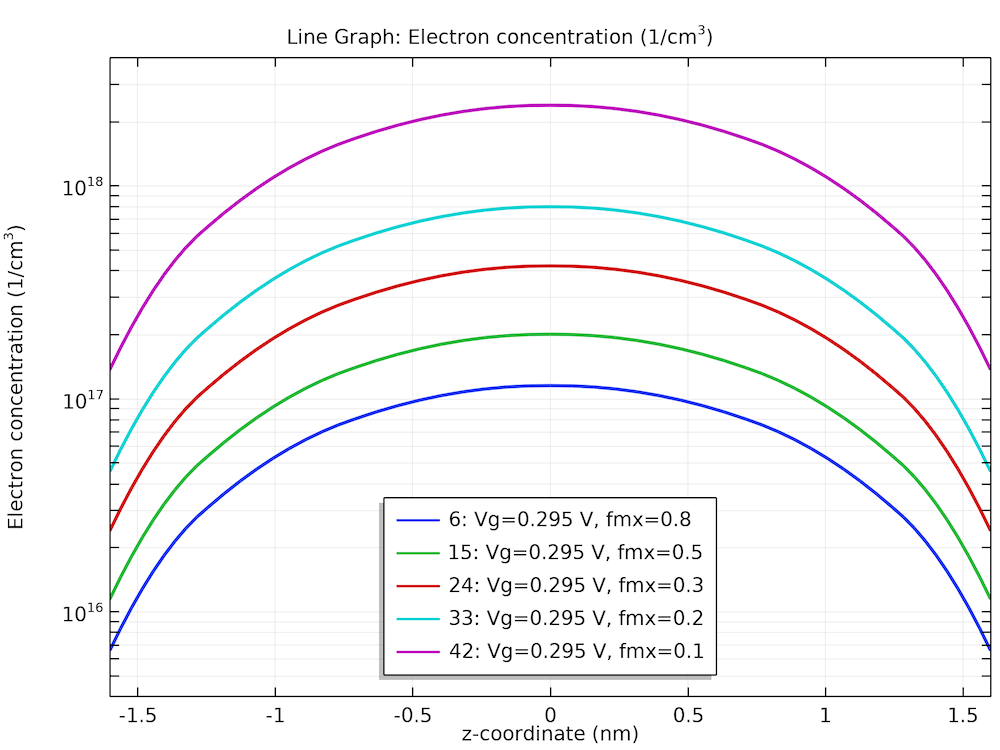
一组密度梯度纵向有效质量的横向电子浓度曲线。

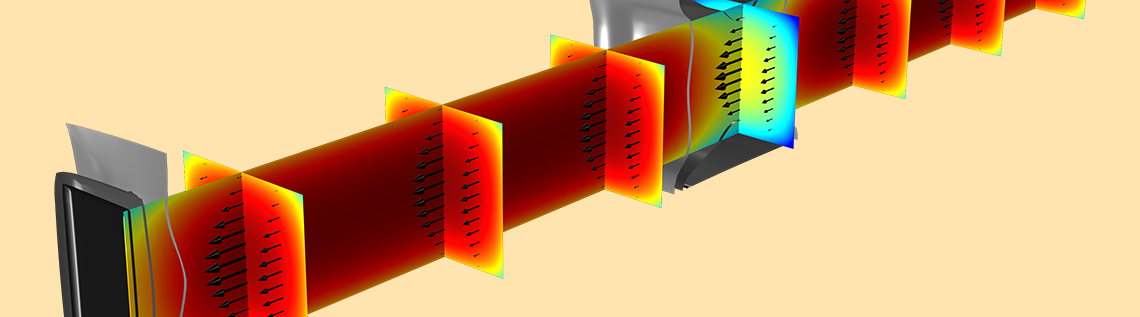
在上面的最后一张图中，氧化物-硅界面的量子约束的影响显而易见。下图是电子密度（彩色切片）、电流密度（黑色箭头）和电势（灰度等值面）的三维分布图。

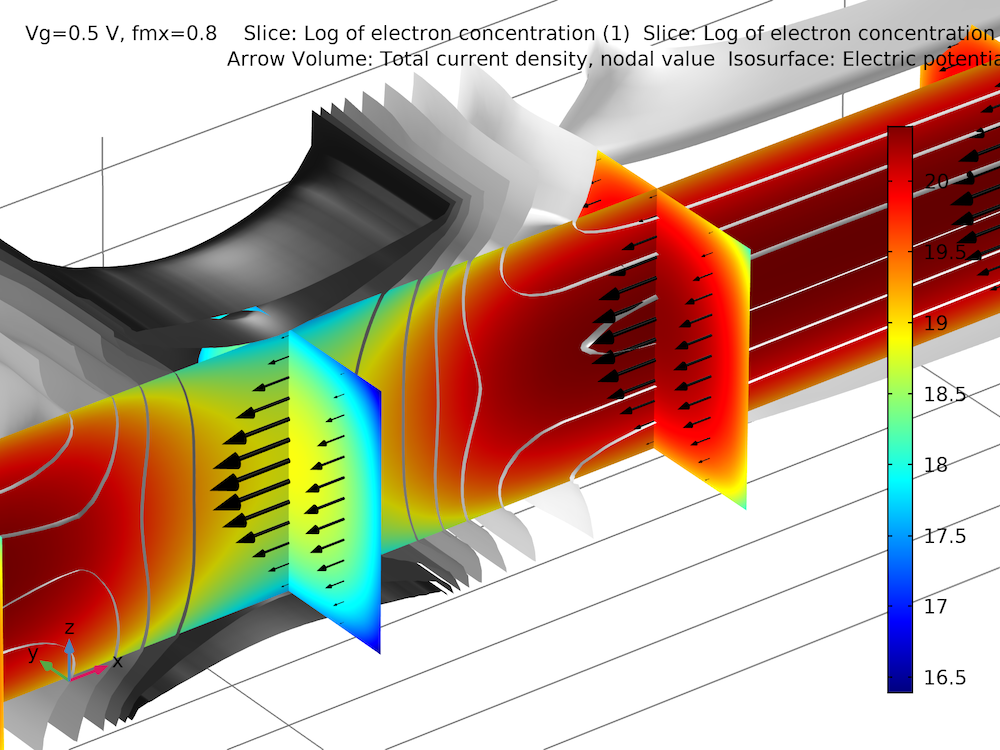
案例 3: InSb p 沟道场效应晶体管

该模型基于文献5建立，分析了具有纳米级沟道的 InSb FET的直流特性。 模拟结构的沟道是由一个5 nm厚的InSb量子阱层在AlInSb阻挡材料上形成的。然后在量子阱层的顶部添加一个10 nm厚的阻挡层，接着是源极和漏极触点的p+帽。温度为300 K，使用费米–狄拉克统计。

在 COMSOL 中，量子阱层的量子约束效应是通过连续/异质结边界条件的默认连续准费米能级选项自动计算的，在连结较好地界面上是有效的。此外，通过选择绝缘边界条件的势垒选项，增加了顶部势垒层边界（顶部势垒–真空界面）的量子约束效应，其方式与前面的例子类似。密度梯度有效质量是各向异性的，其设置方式与上例相同。

参考文献中采用的是一个依赖场的移动性模型。由于其几何结构比较简单，使用电场的X分量来建立移动性模型就足够了。然而，我们选择了更通用的程序，适用于任何任意的几何形状。一个Caughey-Thomas移动模型(E)子节点被添加到半导体材料模型域条件中，用于提供移动性模型使用的电场的平行分量，如下面的截图所示。通过延迟更新电场的平行分量，调整求解器的顺序，以实现所产生的高度耦合系统的收敛。

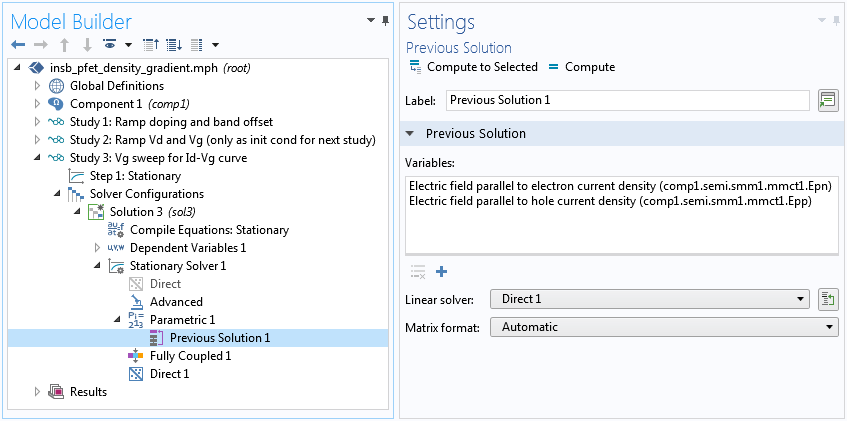
使用求解器序列中的上一个解节点来延迟电场平行分量的更新，以使任意几何在一般情况下均收敛。

下图所示的I-V曲线和空穴密度曲线与文献5中的曲线图一致性极高。

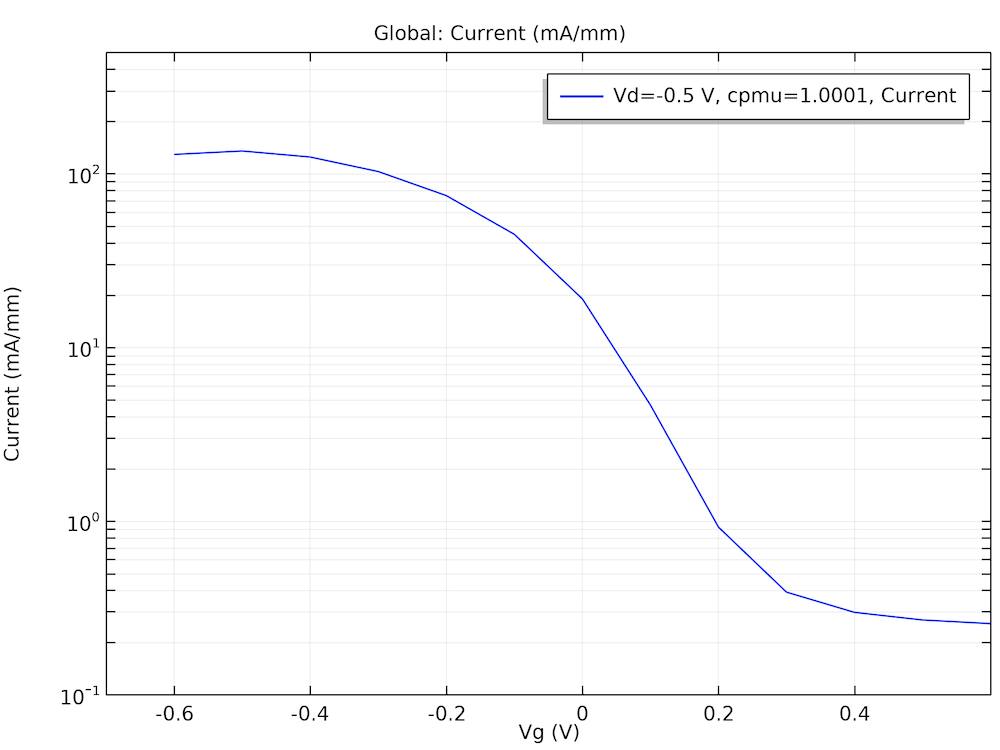
InSb FET 模型的 I-V 曲线

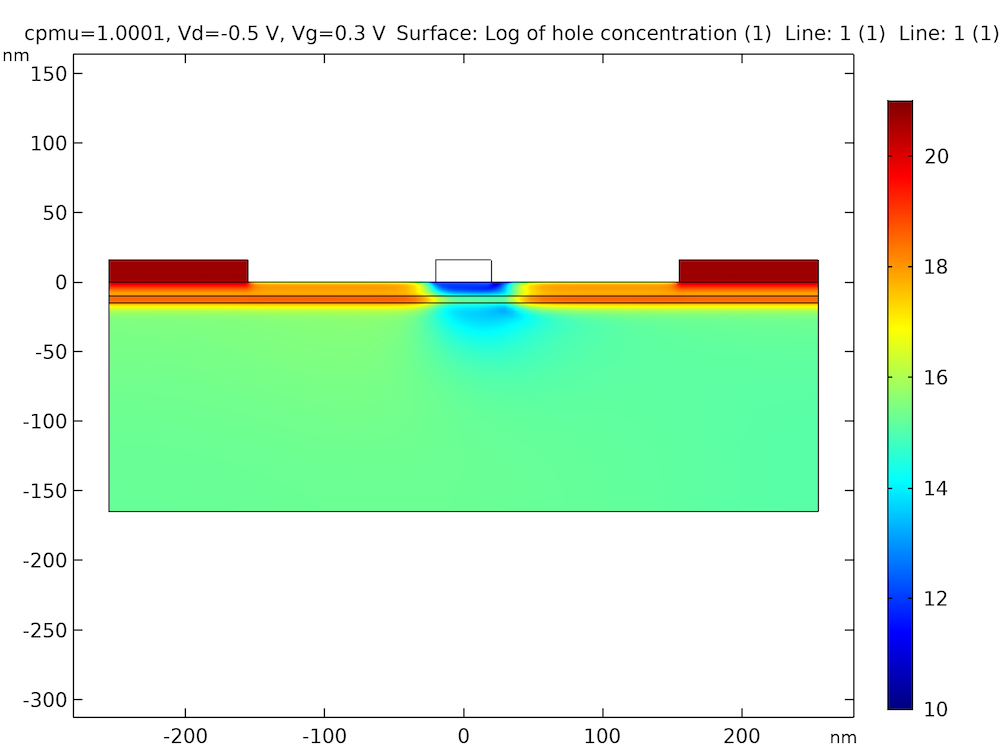
显示量子约束效应的空穴浓度曲线。

下图比较了 x=-100nm 处的空穴密度曲线（蓝色曲线）和近似漂移-扩散曲线（红色点状曲线），用于定性显示量子阱层和顶部势垒-真空界面（y = 0 nm）处的量子约束效应。同时还绘制了价带边缘（“Ev”）和空穴的准费米能级（“Efp”）。请注意，这种比较只是定性的，因为该模型没有使用传统的漂移-扩散公式重新求解。因此，如果模型被重新求解，而绝对量级没有被解决，只有近似漂移-扩散曲线的形状是代表结果的。尽管如此，有量子约束和无量子约束的处理方法之间的定性差异很好地表现在空穴浓度曲线的形状差异上。在异质结处缺乏载流子堆积，以及载流子从顶部势垒-真空界面被排斥，都明显表明了量子约束效应。

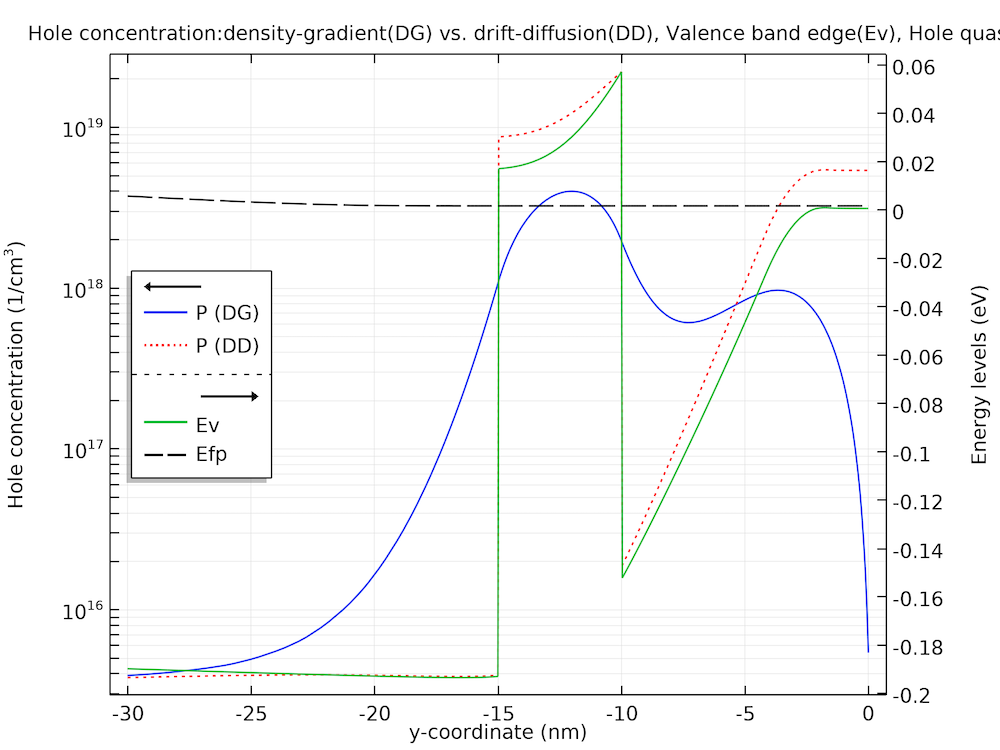
阐明量子约束效应的线性切割图。

结束语

随着晶体管的物理尺寸的不断缩小，量子约束效应已不能被忽视。为了将这种效应纳入器件仿真中，我们在这个系列博客中分两部份介绍了计算效率高的密度梯度理论和一些建模实例。

后续步骤

下载文中介绍的案例模型：

• 硅反转层的密度梯度和薛定谔-泊松结果
• 纳米线 MOSFET 的密度-梯度三维仿真
• InSb p 沟道场效应晶体管的密度梯度分析

想要自己尝试使用密度梯度公式建模吗？请点击下面的按钮与我们联系，获得评估软件的许可证。

参考文献

1. M. G. Ancona, “Density-gradient theory: a macroscopic approach to quantum confinement and tunneling in semiconductor devices,” J. Comput. Electron., vol. 10, p. 65, 2011.
2. M. G. Ancona, “Equations of State for Silicon Inversion Layers,” IEEE Trans. Elec. Dev., vol. 47, no. 7, p. 1449, 2000.
3. A. R. Brown, A. Martinez, N. Seoane, and A. Asenov, “Comparison of Density Gradient and NEGF for 3D Simulation of a Nanowire MOSFET,” Proc. 2009 Spanish Conf. Elec. Dev., p. 140, Feb. 11-13, 2009.
4. S. Jin, Y. J. Park, and H. S. Min, “Simulation of Quantum Effects in the Nano-scale Semiconductor Device”, J. Semicond. Tech. Sci., vol. 4, no. 1, p. 32, 2004.
5. M. G. Ancona, B. R. Bennett, J. B. Boos, “Scaling projections for Sb-based p-channel FETs,” Solid-State Electronics, vol. 54, p. 1349, 2010.