一些仿真问题能得到非常接近实际情况的解。最近,我在为包含非线性电路问题计算时周期性稳态解时,就发现了一个这样的示例。接下来,让我们来深入探讨这个示例,并看看如何借助COMSOL软件的一些核心功能来高效地实现求解。
仿真场景:非线性变压器
在上一篇使用 COMSOL Multiphysics®计算增量电感的博客中,我们探讨了一个由缠绕在非线性磁芯材料上的两个线圈组成的变压器示例。当外加正弦交流电压时,初级线圈和次级线圈会产生感应电流。但是,当电流足够大时,材料的非线性将显著改变增量电感,从而产生非正弦感应电流。我们可以通过建立变压器的全保真模型,或建立考虑了非线性增量电感的等效电路模型来模拟这种行为。非线性使电流随时间呈非正弦周期性变化,我们可以运行瞬态模型多个周期来观察这种逐渐降低到稳定状态的变化。

由缠绕在非线性磁芯上的两个线圈组成的变压器。从有限元模型中提取增量电感,用于等效电路模型中。

运行等效电路模型多个周期后的结果,周期性信号的幅值逐渐接近稳定。
从结果来看,很显然需要模拟多个周期。如果我们只对时间周期稳态解感兴趣,那么大部分生成的数据实际上是不需要的。理论上,在这种情况下我们需要一种能直接获得时间周期解的方法,这正是本文要讨论的内容。
从时间到空间重写等效电路
如果仔细观察该电路模型,我们会发现它只有两个随时间变化的未知数:I_1和I_2, 即通过初级线圈和次级线圈的电流。现在,让我们从电路的范式来思考问题,考虑两个电流回路中各个元件的压降,用以下方程表示
其中,所有增量电感都是两个电流的函数:\partial L_{ij} (I_1,I_2)。这组耦合常微分方程可以用多种方法求解。我们仅求解外加电压为V_{AC},以及方程解的周期为T_0的情况。
很明显可以看出,除了电流的时间导数,这几乎是一组非线性代数方程。但如果用空间导数来代替时间导数呢?让我们看看会发生什么!
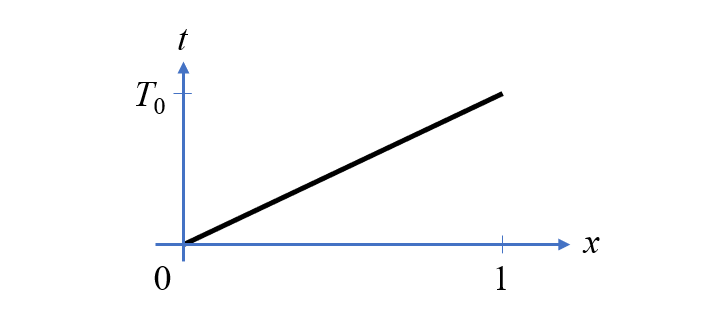
沿一维单元域绘制的时间与位置的函数。
考虑一个一维域,即一条单位长度的直线。定义一个沿长度线性变化的准时间变量。如果在这条直线上定义两个与空间相关的因变量u_1和u_2,并引入网格,那么 COMSOL Multiphysics®软件就可以通过微分算子:d(u1,x)求空间导数\partial u_1 / \partial x。但由于我们将空间维度视为时间维度,因此这实际上是求时间导数。鉴于此,现在可以用域常微分和微分代数方程接口构建一个定义在单位长度直线上的场代数方程。该接口的软件界面截图如下图所示,其中定义了两个未知数。使用拉格朗日单元划分这些场,这会自动确保场的连续性,然后,需要给场和源设置合适的单位。为了便于阅读,还可以定义一组变量来描述电路模型中每个元件所产生的压降,如下图所示。
域常微分和微分代数方程接口设置,包括设置场变量名称、选择形状函数和设置单位。

定义了时间空间的外加电压、电流导数以及电路各元件上的压降的变量。
我们将在域常微分和微分代数方程接口的代数方程特征使用这些变量,该接口包含两个编辑框,需要输入必须始终等于零的方程。在这个示例中,我们输入两个电流回路的电压降项和源项,也就是上文中列出的方程。最后,在域终端的一个点添加两个逐点约束。此处是通过积分特征,在另一个点上定义的约束u1-intop1(u1)和u2-intop1(u2),来实现周期性边界条件。
在单位域输入时间空间的代数方程。
当变压器进入非线性状态时,要求解这个稳态问题,需要在域上设置相对较细的网格。因此,在求解这种非线性稳态模型时,求解域上网格的尺寸是需要测试的参数。稳态模拟结果如下图所示,将其与瞬态结果进行比较,结果显示二者非常吻合。事实上,当以更严格的容差求解瞬态模型时,二者之间的差异就越小。但即使是这样一个小模型,高精度的计算都会显著增加瞬态计算的成本,而稳态计算几乎可以瞬间求解。

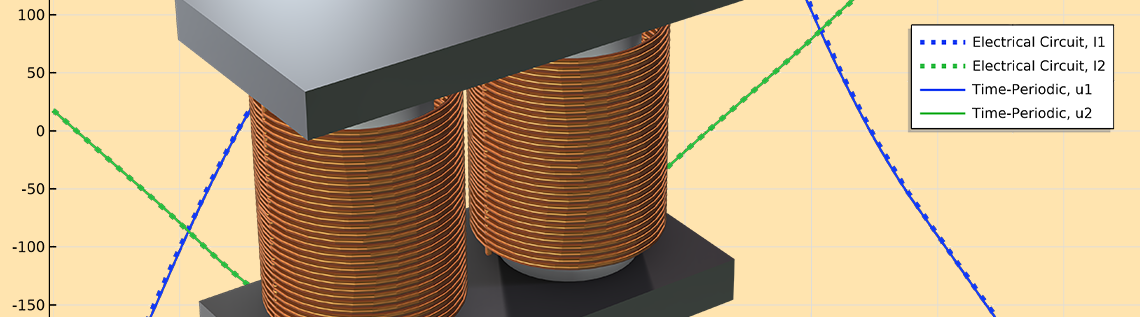
电路模型计算出的瞬态结果与使用时间周期方法计算的稳态结果的对比。
通过空间 FFT 数据集特征,我们还能使用空间中一个周期的解提取频率组成。该特征的设置如下图所示,其中突出显示了一维阵列数据集,该数据集会对计算结果进行周期性扩展,使结果看起来更加平滑。通过绘制适当归一化处理的量,我们可以看到频率组成如何随着外加电压的增加而增加。

空间 FFT 数据集将一维阵列数据集作为输入,周期性的对稳态计算结果进行拓展。
结束语
这篇博客,我们介绍了一种特别高效的方法,求解用一组代数方程描述的系统的周期性稳定解。需要注意的是,只要存在平滑的周期性解,这种方法就可以使用任何类型的应用信号,而不仅仅是正弦强制函数。此方法设置非常简单,并且利用了 COMSOL Multiphysics®的核心功能,因此适用于任何类型的问题,而不仅是电路问题。对于使用COMSOL 的仿真人员来说,这是一项非常有用的仿真技术。
您可以点击下方按钮,下载相关示例模型:



评论 (0)