使用 COMSOL Multiphysics® 模拟自由液面的两种方法

COMSOL Multiphysics® 软件提供了四种可用于模拟自由液面的方法：水平集、相场、动网格和稳态自由表面。作为系列博客的第一部分，本文我们将讨论水平集和相场法，这两种基于场的方法几乎可以描述任何类型的自由液面。在第二部分中，我们计划将本文的求解结果与通过动网格方法获得的结果进行比较。

何为水平集和相场法？

水平集和相场法都是基于场的方法，这类方法通过水平集或相场函数的等值面来表征自由液面，对应于固定网格框架下的液体和气体之间的相分界面。

下图为一个管道内的两颗液滴的表面，摘自微流体模块案例库中提供的液滴破碎模型。从这张图中可以看出，尽管液滴的表面非常清晰，但液滴周围的网格单元并没有贴合到液滴表面。

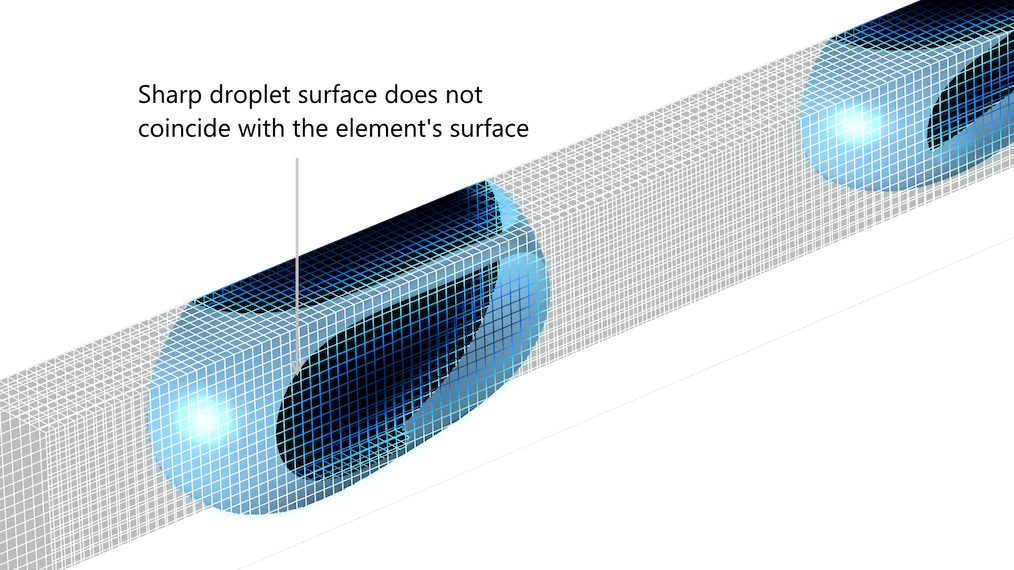
不管采用水平集方法还是相场法，液滴表面与单元表面都不贴合。

水平集和相场函数都随速度矢量进行对流，后者可由纳维-斯托克斯方程计算。在水平集和相场法中，使用的方程为：

(1)

需要注意的是，水平集和相场函数都使用了Φ，二者的不同在于方程右侧的F。在初始水平集方法中F=0，因此得到纯对流传输方程。然而当F=0 时，数值解不仅不稳定，而且大部分情况下实用性很小。所以为了保持相界面清晰，我们在水平集方法的F中添加了高阶导数项Φ。

在相场法中，F代表设法将系统的自由能最小化的项，此项也引入了高阶导数Φ。实际上，相场方程中的源项中包含了四阶项。这意味着，出于实用性考虑，方程经常被分解为两个方程，与此同时，辅助因变量被定义为Φ的二阶导数函数形式。COMSOL Multiphysics 中也采取了这种做法。

两种方法均将自由液面的表面张力引入到纳维-斯托克斯方程的源项中。水平集方法利用表征自由边界的水平集等值面的曲率来描述表面张力。相场法根据化学势计算出表面张力对纳维-斯托克斯方程的源项贡献，因为正是化学势导致了界面附近表面张力和相场函数梯度的产生。

在给定的水平集或相场函数值范围内，即自由表面的数值范围内，流体特性从液体平滑地过渡到气体。

穿过自由表面，水平集函数Φ在 0 和 1 之间变化，在两种流体内部分别为常数 0 或 1。比如在液相中为 0，气相中为 1。至于自由液体面处，也就是液体和气体之间的分界面，对应的水平集函数值为Φ=0.5。根据下方公式，密度是水平集函数的函数：

(2)

动力黏度也与水平集函数有关：

(3)

从这两个方程中我们可以看出，当Φ=0 时，可得到流体 1（比如液体）的属性，当Φ= 1 时，可得到流体 2（比如气体）的属性。由此，流体属性在整个自由表面上实现了平滑过渡，像水平集函数一样平滑。

相场函数Φ在 -1 和 1 之间变化，当Φ=0 时的等值面为自由液面。黏度和密度是通过与水平集法相似的方式完成计算的，只不过因为相场函数在 -1 和 1 之间变化，所以表达式不同。

水平集与相场接口的设置

COMSOL 内置的水平集和相场接口中包含若干个参数，为了使计算取得最优效果，我们需要对这些参数进行调整。参数的值取决于被模拟的系统和方程的数值离散。几何结构的尺寸（长、宽、高）、流体的特性、壁的润湿条件、初始条件、工作条件，以及网格的单元尺寸都会对模型设置选项产生影响。

水平集接口

我们从水平集方法的设置开始。重新初始化用户界面中的参数γ，可以确保水平集函数中的梯度会随着时间的推移逐渐集中到自由表面，也就是下方示例中水和空气之间的交界面。我们没有设定表面厚度，但能够确保水平集函数的变化在厚度范围之内。如果该参数值设置过低，水平集函数的变化可能会被截留在一种流体域内，然后凭空生成液-气界面。设置过高的值则往往会造成时间步过小、计算时间过长。

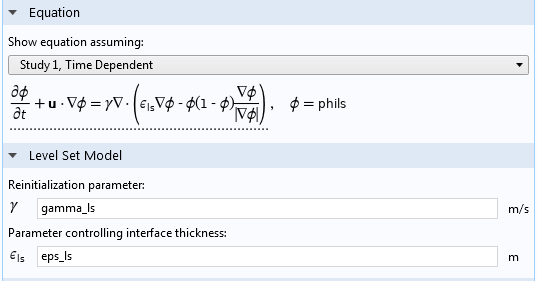
水平集接口的设置窗口。

参数ε代表界面厚度参数，理解起来更加直观，它唯一的作用是控制水平集函数发生变化的区域的厚度。过厚会模糊自由表面的形状。虽然这让问题变得更容易求解，但是损失了自由表面的形状精度。较小的ε值有利于生成清晰的表面，但这也要求网格具有相应的分辨率。设定小于网格单元尺寸的值是没有意义的，因为这会使得界面变得不规则，而无法解析的表面张力可能会导致速度失真。ε的设定值应与表面附近的最大单元尺寸接近。

相场接口

接下来介绍相场法，其界面厚度参数ε的设置与水平集方法基本一致，前文中的论证同样适用于此处的设定值。

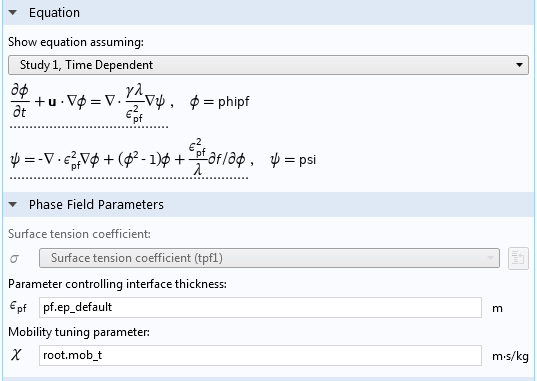
相场接口的设置。

相场法的迁移调整参数χ在某种程度上决定了相场的扩散系数。它的值必须足够大，才能保证相场方程稳定，但是为了保证表面清晰，也要足够小。合理的值与表面速度成正比，与表面张力系数成反比。

(4)

这意味着一旦确定了某组工作条件的χ值，就可以利用上述关系为一组新的条件设定χ的值。

模拟自由液面

通过下图中的示例问题，我们将演示如何在 COMSOL Multiphysics 中利用水平集和相场法模拟自由液面。

如下图所示，将一个矩形实心条的一半浸没在小型管道内的水中。沿与水面相切的方向来回移动实心条，使水面产生柔和的波浪。为了保持层流状态，管道和实心条的尺寸必须足够小。

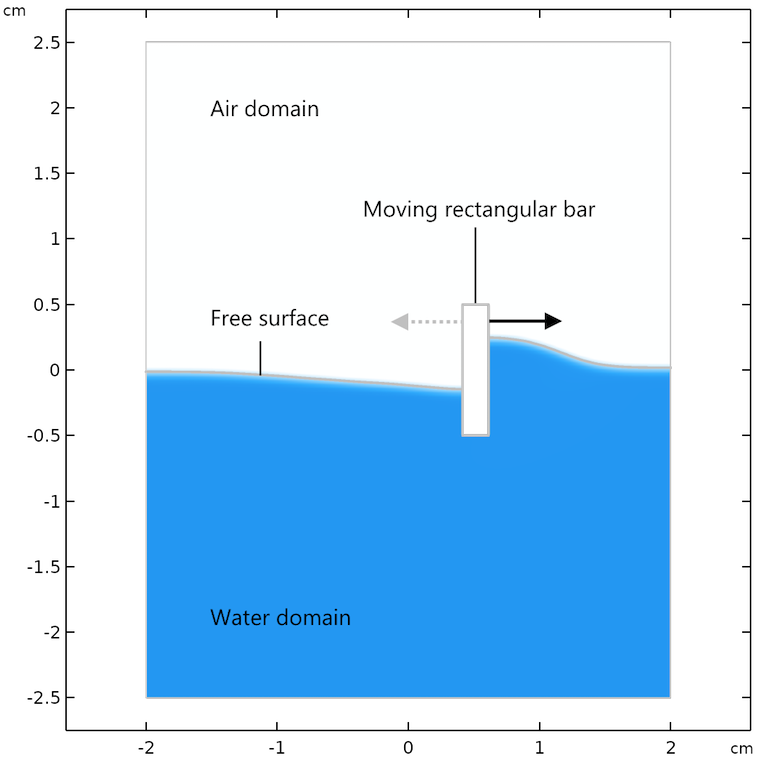
示例问题的几何结构和定义。

在此例中，我们使用动网格功能指定小矩形条在水面上反复运动。但是，在水平集和相场法中，网格不会随液体表面移动。

下面是关于在 COMSOL Multiphysics 中创建模型的几点备注：

• 添加重力作为动量方程的源
• 添加参考压力和压力约束点
• 为了方便比较结果，对壁应用 Navier 滑移条件，并使滑移长度等于单元长度

水平集与相场法的仿真结果

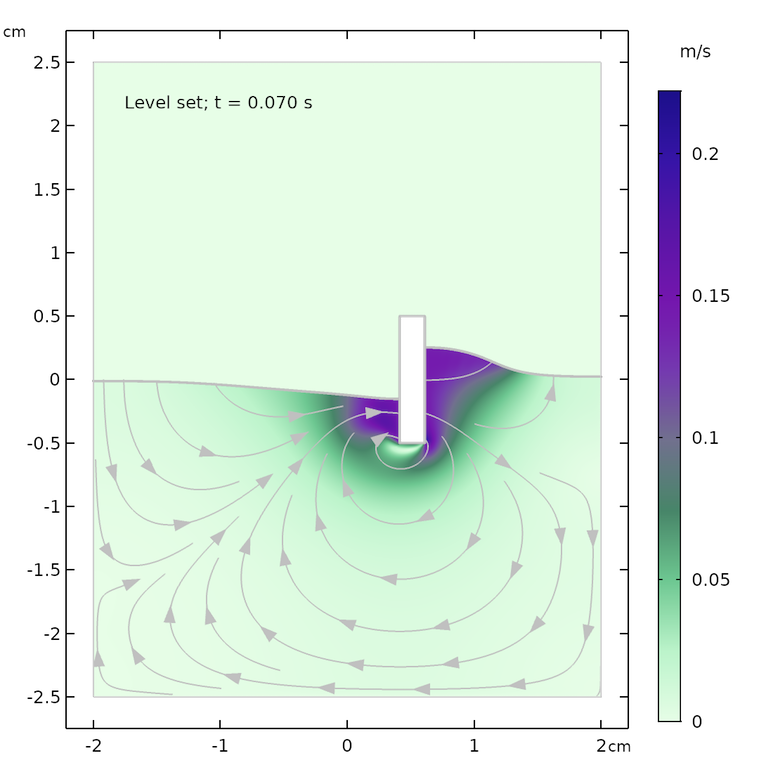
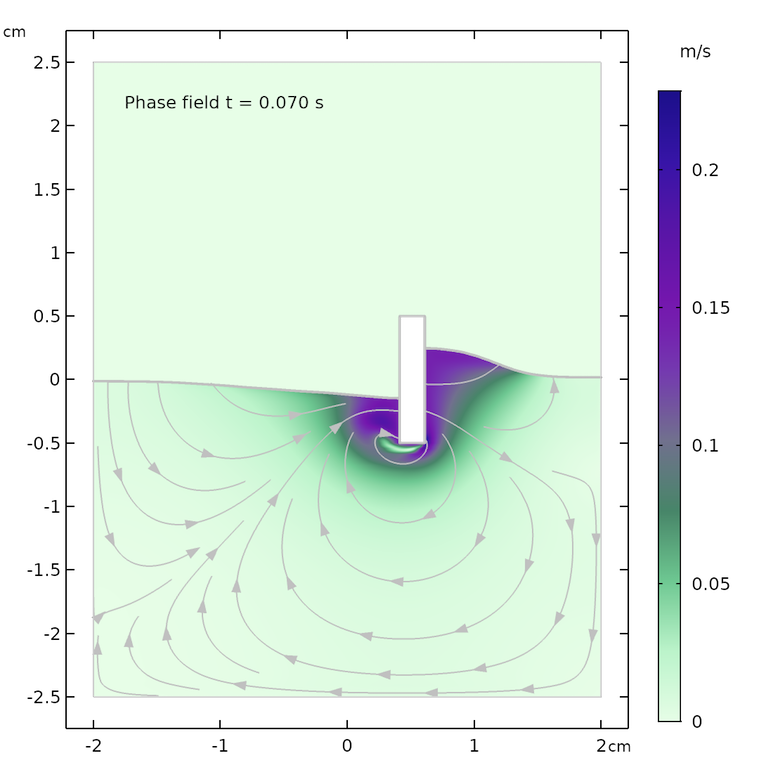
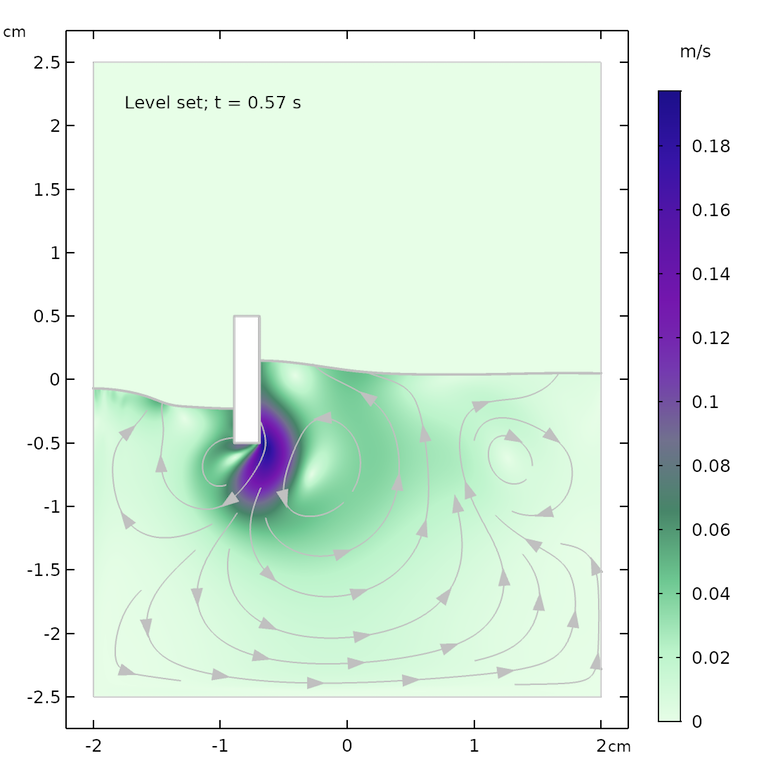
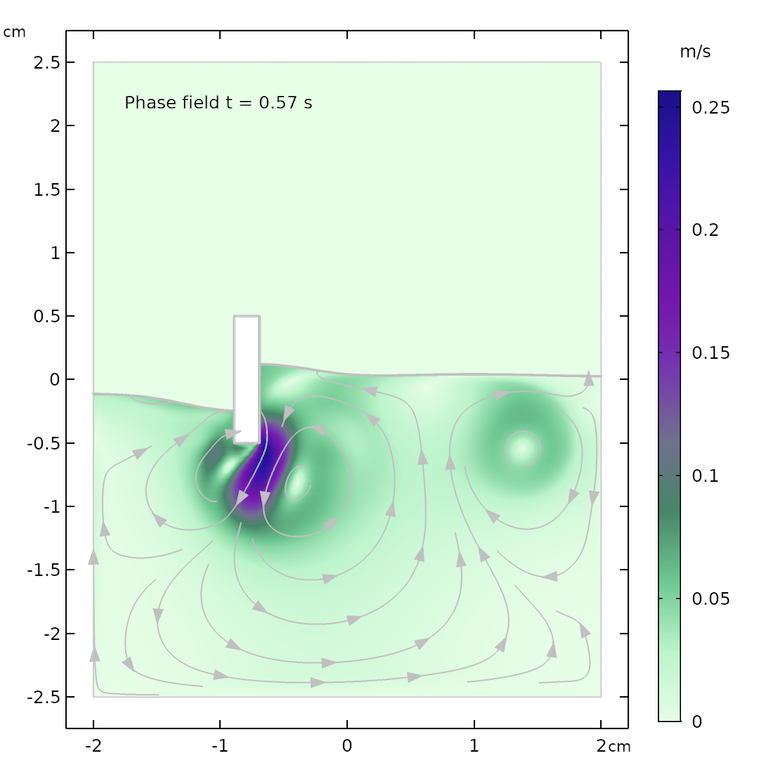
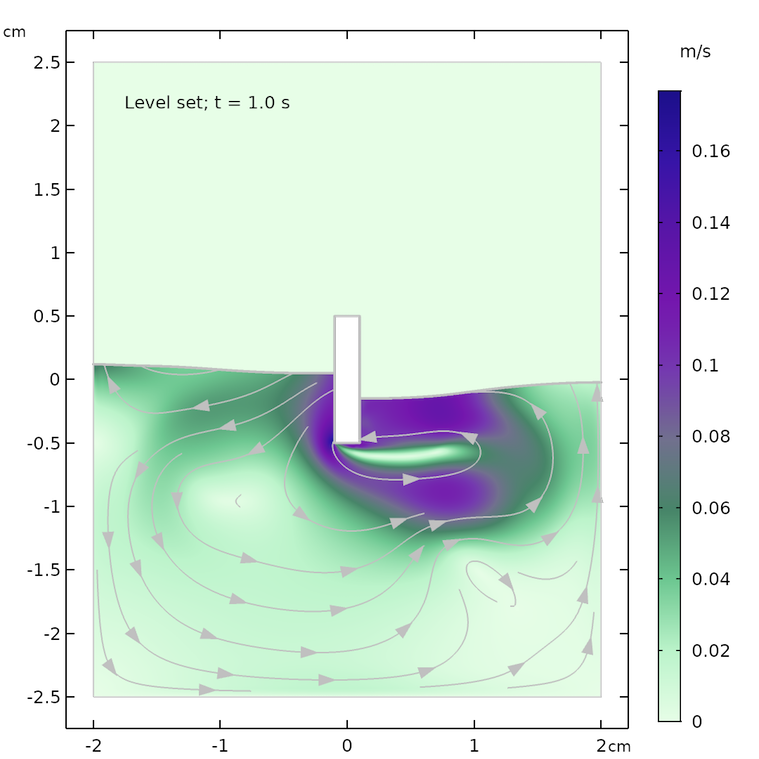
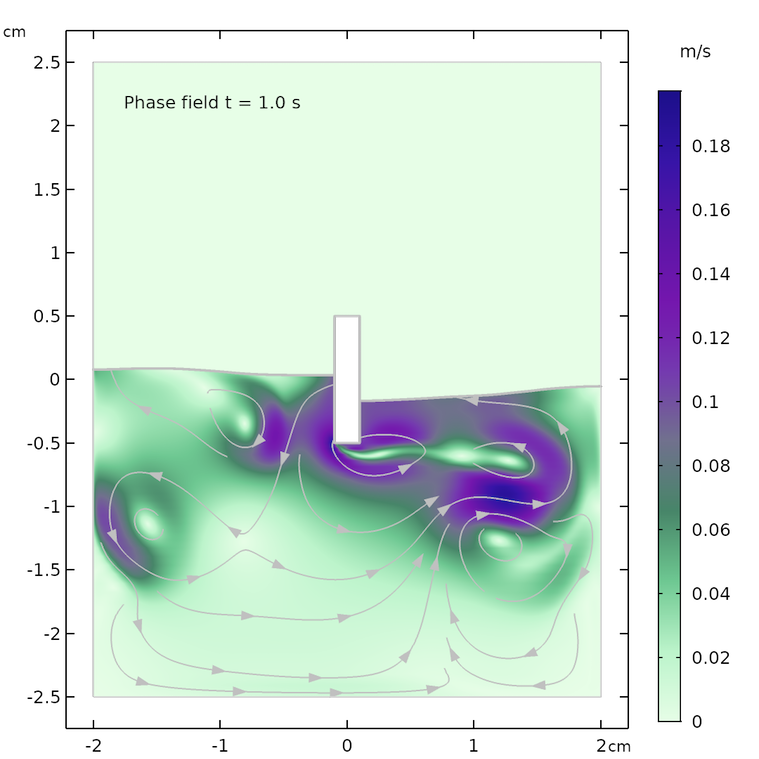
下方结果图显示了 0.07 s、0.57 s和 1.0s 后，分别采用水平集与相场法进行模拟的流场和水面形状。两种方法在各个时间点上的流线和水面形状均大致相同。最大速度和水面高度稍有差异，原因可能在于两种方法处理表面张力的方式不同。

再经过一段时间后，流线也出现了差别，例如 t = 1.0 s 时的回流区。通过相场法得到的液面相对更加平静。水平集方法利用基于水平集函数的梯度获得的表面曲率来计算表面张力。所以，与相场法中更加平滑的力相比，水平集方法得到的表面力更“尖锐”。

0.07 s（上图）、0.57 s（中图）和 1.0 s（下图）后，分别采用水平集（左图）和相场（右图）方法得到的模拟结果。

我们可以通过动画完整地展示 0~2 s之间的结果。可以看到，尽管矩形条的运动引起了剧烈搅动，但是表面从未断裂。

通过动画演示相场法的求解结果。

水平集和相场法还能计算自由液面上的空气域流场。从图中可以看出，矩形条的运动在整个相界面上方引起了持续显著变化的流场。

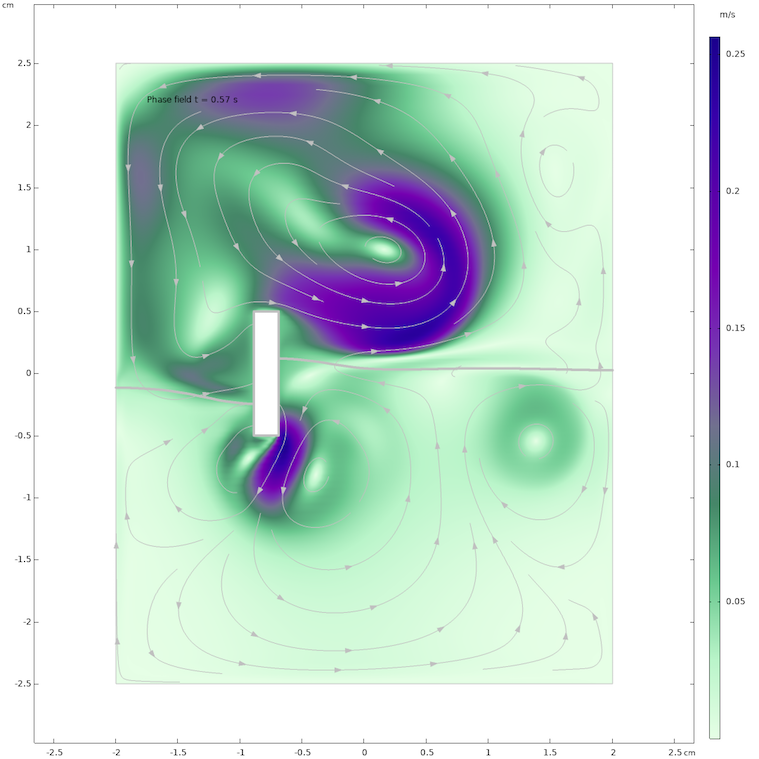
利用相场法计算 0.57 s 后水域和空气域内的流场。

如果增强搅动能使液面运动更剧烈，那么液面可能先破裂再合并，如下方动画所示。这也是水平集与相场法的一个优势：能够更简单地处理自由表面的拓扑变化。

矩形条的搅动频率和幅度增大，使较小的波浪破裂，并生成了滞留在水相中的气泡。

尽管水平集和相场法的模拟结果类似，但表面张力的处理对二者的稳定性产生很大的影响，至少在 COMSOL Multiphysics 中存在区别。在处理对表面张力非常敏感的问题时，相场法在求解时间方面比水平集方法表现得更好，原因是利用水平集方法计算表面曲率时，瞬态求解器需要采用比相场法小得多的时间步。

在此例中，水平集方法的平均时间步是相场法的六倍，所以水平集方法需要比相场法多六倍的计算时间。因此，对于较小尺度自由液面问题和对表面张力极其敏感的层流（例如微流体）问题，相场法通常是更好的选择。

自适应网格细化与自由表面

针对本文探讨的二维示例，在采用了水平集和相场法的整个自由表面区域中，网格足够密集。不过，对于三维模型而言，这种水平的分辨率计算成本太高。一种替代方案是使用自适应网格细化功能，它能够自动根据我们选择的任何函数创建更密集的网格。

举例来说，下方动画展示了基于最大速度梯度的位置（左图）和相场函数的最大梯度（右图）生成的网格自适应结果。绘图展示了气相和水相。需要注意的是，与剪切率相关的自适应网格在气相中生成了细化网格，而水相的细化程度相对较低。在此例中，我们对水相更感兴趣，因此需要通过缩放相场函数来修改自适应网格的误差指示器。

利用速度梯度（左图）和相场梯度（右图）作为误差指示器的自适应网格细化效果。

动网格与自由表面

本文讨论了两种基于场的自由表面仿真方法：相场法和水平集法。在此系列的第二篇博客中，我们将使用动网格来模拟自由表面，并对两篇文章介绍的方法进行比较。敬请关注！

更新：第二篇已经发布，欢迎点击阅读。

后续操作

单击下方按钮，了解 COMSOL Multiphysics 附加产品——CFD模块中与流体流动仿真相关的专业功能。

延伸阅读

• 动手操作：在案例下载页面中下载 MPH 文件
• 阅读博客，了解水平集与相场法的其他实际应用：
  • 模拟掉落在水面上的球体
  • 设计可实现材料精确沉积的喷墨打印头

编者按：本文在 2018 年 5 月 25 日的更新中增加了一个链接到案例下载页面的 MPH 示例模型。