COMSOL 博客

使用仿真探讨黏性悬链线问题

2017年 3月 22日

近年来，黏性悬链线问题已引起学术界在理论和实验研究方面的兴趣，因为这个丰富的现象在工业有着重要的应用。利用 COMSOL Multiphysics^®软件的灵活性，我们可以获得对复杂问题（如黏性悬链线问题）的基本了解，并验证已有分析中所作假设的有效性。

悬链线的历史意义

在数学和物理领域，悬链曲线具有重要的历史意义。它不仅突显了几何学和力学之间的关系，而且在结构工程中也起着重要作用。

悬链线（Catenary）源于拉丁语中的“链条”，描述了理想化链条或缆线所呈现的曲线状形状，该链条或缆线在它自身的重量下悬挂在两端的支撑物上。1670 年代，英国科学家兼建筑师 Robert Hooke 研究了这种几何形状的特性。在这段时间里，他意识到该曲线代表了具有恒定横截面的拱的最优形式。尽管 Hooke 知道悬链线的形状不同于抛物线，但直到 1690 年，其他研究人员才确定了它的数学形式。

Robert Hooke 的绘画，画中的链条形成悬链曲线。
Robert Hooke 手持着一根链条，形成一条悬链线。图片由 Rita Greer 提供。通过Wikimedia Commons，获Free Art License 1.3 许可。

如今，悬链曲线出现在各种结构中，例如自由悬挂的电缆和悬索桥。同时，许多拱形结构类似一条倒悬链曲线，它的形状可以指导结构中材料的分布。通过将重力转化为整个拱形结构内部的挤压力，这些设计能够承受自身的重量。

形成悬链线的自由悬挂的电缆。
自由悬挂的电缆呈现出悬链线状态。图片由 Loadmaster(David R.Tribble）提供。通过Wikimedia Commons在CC BY-SA 3.0下获得许可。
具有倒悬链线结构的室内花园。
许多其他结构中使用了倒悬链曲线，包括 Sheffield Winter Garden 冬季花园中的拱门。图片来源：Wikimedia Commons公共领域。

探索黏性悬链线问题

到目前为止，我们已经讨论了与固体材料有关的悬链曲线。但是当材料是流体时会发生什么呢？解决这类问题可能会有些复杂。

黏性悬链线问题描述了由高黏性流体组成的圆柱体如何在重力的作用下流动，此圆柱体的两端固定。这一过程出现的物理现象在工业中有一系列重要的应用，包括玻璃制造、纺丝生产。因此，黏性悬链线问题已经在学术领域引起了广泛的理论和实验研究兴趣。

过去，研究人员已为黏性悬链线问题提供了一维解决方案（请参阅模型教程中的参考资料）。为了进一步了解该问题并解决已有研究中假设的有效性，我们可以在 COMSOL Multiphysics 中运行我们自己的模拟测试。下面，让我们通过研究微流体模块中的教程，来探讨这个问题。

设计一个黏性悬链线模型

该黏性悬链线模型是一个圆柱体状的牛顿流体，重力方向朝下。其设计具有以下特性：

初始直径：0.6 mm
长度：21.5 mm
流体密度：1000 kg / m³
黏度：100 Pa·s

结构内部流体的表面张力为22 mN /m。

由于流体流动过程中，毛细管数较高，所以流体与壁面之间的接触角不重要。因此，我们使用 90º 的标准值。此外，在每个表面上添加“滑移”边界条件，可以使圆柱体的支撑边缘稍微移动。相比于圆柱体的总位移，该位移相当小，可以根据需要从结果中忽略。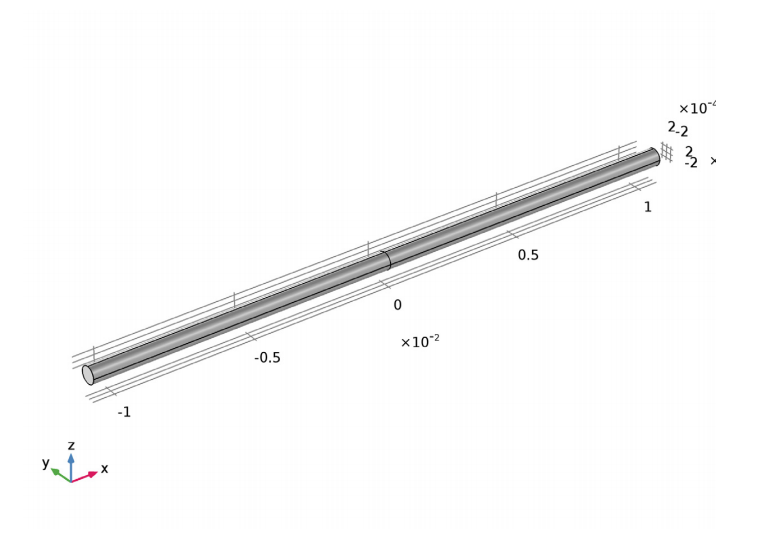
一个充满黏性流体的圆柱形模型示意图。
模型的几何形状。

如图中突出显示的，圆柱体被分为两半，因此可以在结构的中心设置点。然后，使用这些点来计算悬链线最低点的高度。

评估和比较仿真结果

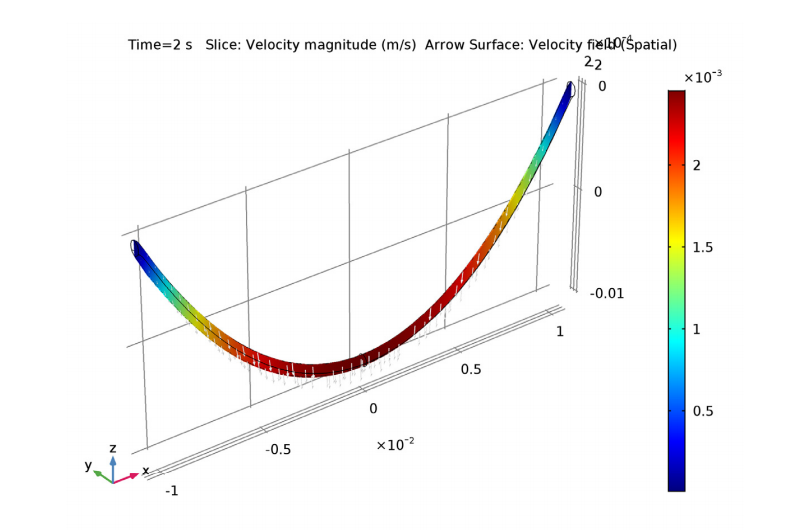
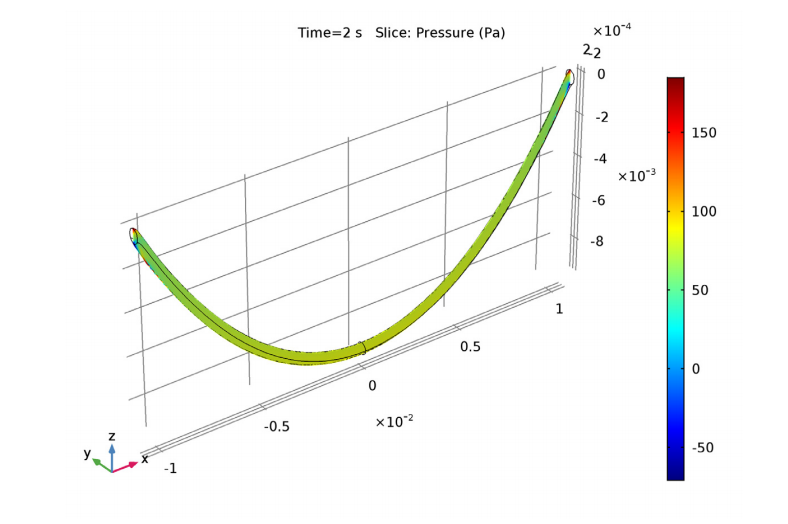
降落 2s 后，测量悬链线的流速。结果表明，流体速度方向主要是垂直的。从曲线内部的压力来看，在靠近端点（固定点）的小区域内，压力的变化最显著。两个端点是曲面曲率半径最大的点。

悬链线内部的流体速度（左）和压力（右）。

下图显示了悬链线中心线位置与时间的关系，间隔为0.02 s。在悬链线长度的中心部分，抛物线轮廓很明显。中等时间尺度下的一维理论可以预测这种效果。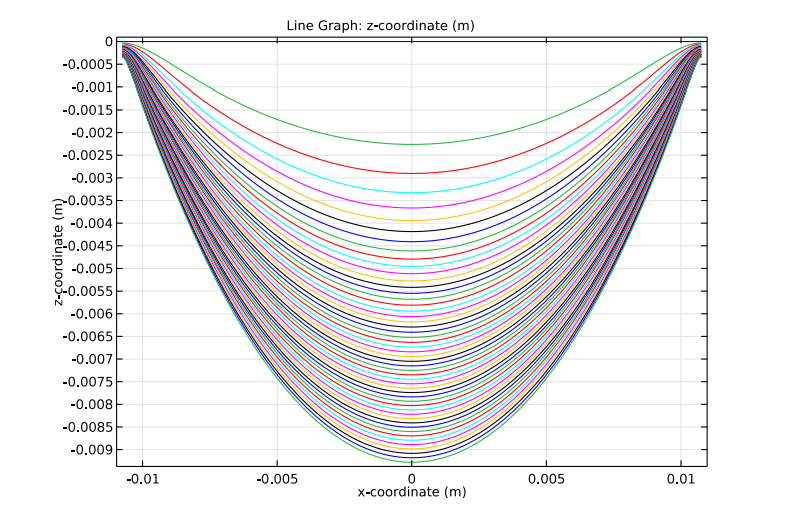
在COMSOL Multiphysics®中绘制悬链线中心线位置的图。
悬链线中心线的位置。

由上图，我们可以观察到悬链线中心线与其端点之间的垂直距离随时间的变化情况。将仿真结果与实验数据进行比较（参考文献 2，模型教程），两者之间具有较高的一致性。请注意，这不包括之前研究中用于与所提出的理论达成一致的比例因子。对表面张力系数执行另一次参数扫描，表明此比例因子与表面张力相关，而在之前的理论处理中则忽略了这一因素。

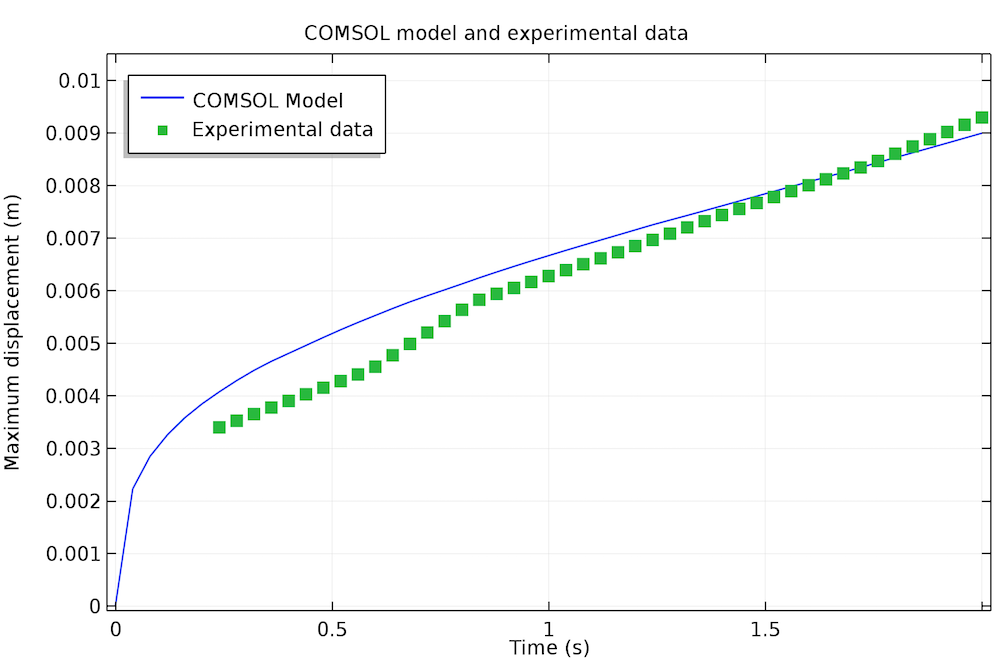
悬链线中最大位移的仿真结果与实验数据的对比分析图。
悬链线中最大位移的仿真结果与实验数据的比较。