使用自适应网格划分进行局部解的改进

如何选择网格是有限元建模中一个长期存在的问题。我们希望选择一个足够细的网格以获得准确的解，但又不能太细，因为这将导致过多的求解时间。我们在之前的博客文章自适应网格细化可以改进网格中讨论过，默认情况下，它能使模型的整体误差最小。然而，我们往往只对整个模型空间的某些区域的精确结果感兴趣。今天我们将介绍一种基于局部指标的网格细化技术。

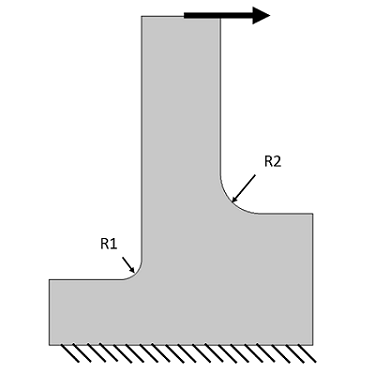
具有全局网格细化的模型

我们来看一个简单的机械问题——一个固定在底部并在顶部施加载荷的支架。应用了两种不同的圆角半径，因此很难预测峰值应力的位置。我们先使用默认的二阶单元，在一个极粗的网格上解决这个问题，然后观察结果。可以看到峰值应力位于半径较大的圆角处，并且该网格似乎很难获得解析解。

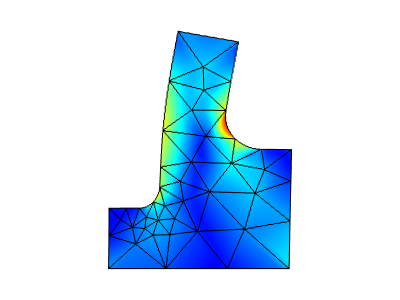
在粗网格上求解的应力和变形。

为了获得更准确的解，我们可以转到适用于稳态、频域和特征值研究步骤的自适应和误差估计设置。下面的屏幕截图为这些设置的示例。默认情况下，误差估计基于最小化误差 L2 模的平方，这是一个全局指标。也就是说，重新划分网格将减少模型中各处的误差。（注：5.6 版本后此方法已经改为：通用修改），它将在需要较小单元的区域细化网格，但也可以在不需要细网格的地方粗化网格。默认情况下，这种自适应细化将进行两次。但是，在下面的屏幕截图中，总共细化了四次。

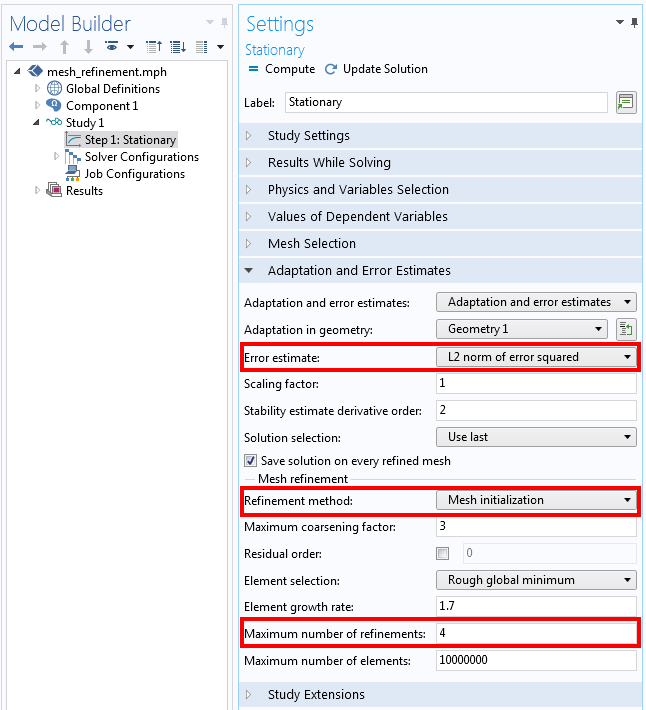
自适应网格细化设置以减少模型中的全局误差。相关设置用红色框突出显示。

上述自适应网格细化的结果如下所示。请注意网格是在整个域中非常均匀地被细化的。可以看到，应力场明显比我们的原始网格更平滑。

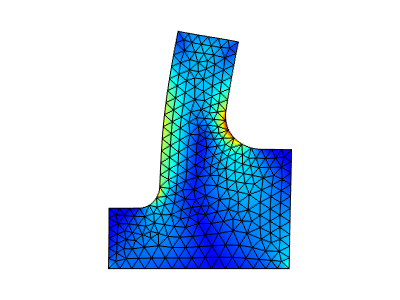
使用误差 L2 模的平方作为误差估计的自适应网格细化的结果。

基于局部解的自适应网格细化

考虑相同的问题，但对自适应网格细化使用不同的方法。从粗网格中，我们已经初步可以看到最大的应力位于较大半径的圆角处，因此可以设置自适应网格细化算法来解决这个位置的应力。将误差估计切换到泛函，这里要求我们输入一个用于改进网格的泛函数。泛函可以是基于解的任何可微分标量。我们将使用的函数是模型变量 von Mises 应力沿边界的积分comp1.solid.mises。这里名为comp1.intop1()的积分耦合算子定义在较大圆角的边界处，如下面的屏幕截图所示。

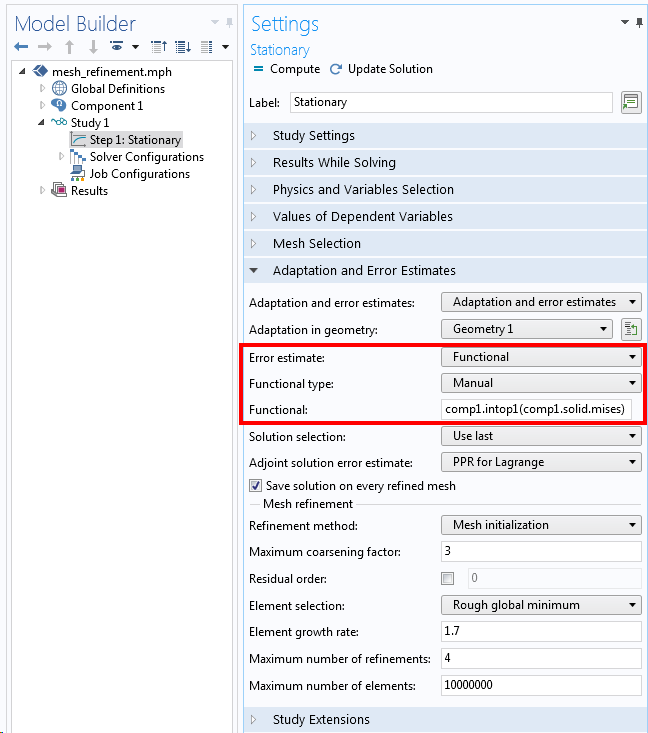
自适应网格细化设置可减少模型中某一位置的局部误差。

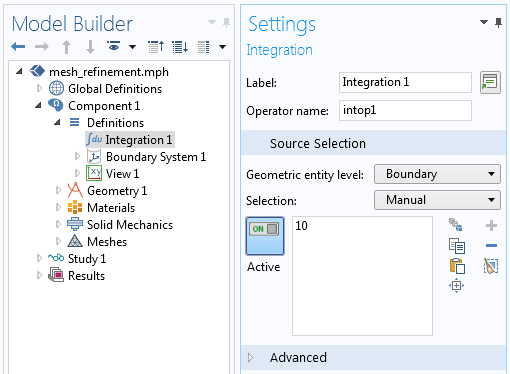
积分耦合算子用于定义我们将评估的边界应力。

查看这种方法的结果时，我们应该注意到细化网格的两个特征。首先，它优先在我们选择的圆角边界周围插入较小的单元。这是预料之中的，因为我们正试图在该区域获得更准确的结果。然而，我们还观察到网格在模型的其他区域也得到了细化，而不仅仅是在我们感兴趣的边界处。自适应网格细化算法将全局调整网格以更好地求解局部应力，而这些应力取决于模型中其他地方的解。

还可以看到，使用手动网格细化来预测峰值应力可能非常困难，因为我们通常无法轻松确定模型的哪些其他部分可能会影响我们的解决方案。

基于局部泛函误差估计的细化网格。

结论

您已经看到，我们可以指定一个局部量来进行自适应网格细化，软件将细化网格以在局部提供更好的结果，同时也会细化模型其他区域的网格，这些区域的网格质量可能不是您当前特别关注的。本文介绍的技术是一种强大的方法，您可以使用它非常自信地进行网格细化。

编者注：此博文于 2017 年 8 月 21 日更新。