
前些天我遇到了一个有趣的问题,它促发了我想要写一篇博客的灵感,因为它使我想到了我们的 COMSOL Multiphysics 软件中一个非常强大但常常没有得到充分利用的功能:全局方程。在这篇文章中,我们将讨论如何使用全局方程为模型引入一个额外的自由度,来表征一些并不想明确建模的东西。
建模场景
假设有一个小房间,里面有一个人,如下图所示。房间内有一个风扇使空气循环流动并充分混合,因此可以假定房间内空气温度是恒定的。假设室外有微风,并且我们知道室外的空气温度。我们还假设地下的地面温度是恒定的,普通人在休息时会散发大约 75W 的热量。建模目标是计算房间内的空气温度以及通过墙壁的温度梯度。
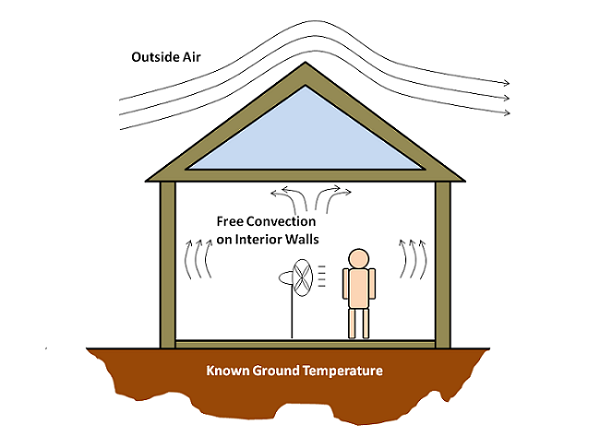
模型设置
如果你想要非常精确的建模,可以建立一个共轭传热模型,并求解房间内部和周围的温度场和流体流动。(如果你想建立一个房间内所有气流的模型,请参阅“置换通风”案例模型)。
然而,与求解传热问题相比,求解流体流动问题对计算要求很高。如果你熟悉传热建模,就会知道对于垂直和水平壁,可以通过一个方程q”=h(T_{air}-T)将内向热通量q”、墙壁温度T、空气温度T_{air}和传热系数h联系起来。如果空气温度高于墙壁温度,热量将流入墙壁,反之亦然。因此,使用该方程,我们根本不需要求解流体流动,就可以知道室内的空气温度。我们用一个简化的工程草图来说明如何建模:
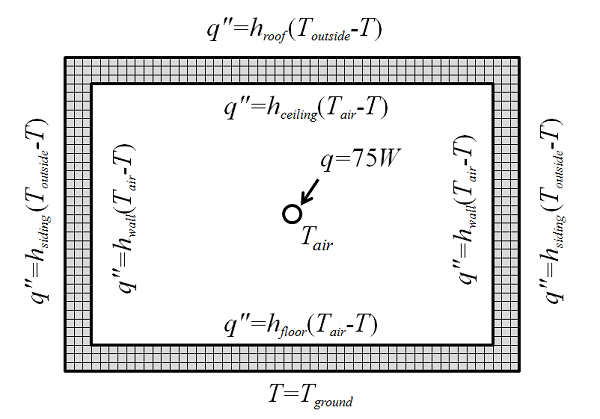
这里,我们使用有限元方法对房间壁进行了具体建模;我们使用了真实的墙壁尺寸,并设置了适当的材料属性。求解的场是墙壁的温度,我们将它假设为稳态条件。我们知道室外温度、地面温度和所有传热系数,因此这个问题几乎是可以求解的。但是我们不知道房间内的空气温度T_{air}。因此,空气温度需要作为一个额外未知数添加到有限元模型中。
除了未知数,我们还需要知道该变量必须满足什么等式。在这个示例中,选择很明确:我们要确保进出空气域的所有热量之和等于零。也就是说,如果我们对室内墙壁和空气之间的热通量进行面积分,再加上人的热量贡献,那么这个积分应该等于零:
使用全局方程求解模型
全局方程接口提供了一个变量名称输入列表(我们将使用Tair)和所要满足的方程。在定义方程的字段中,我们将使用名为intop的积分耦合算子对所有墙壁边界的法向总能量热通量变量ht.nteflux进行积分。由于这是一个稳态问题,我们给定的初始条件并不重要。在设置时,请确保打开模型开发器中的高级物理场选项,以便在物理场接口中添加全局方程。在求解全局方程时,需要使用全耦合方法和直接求解器。
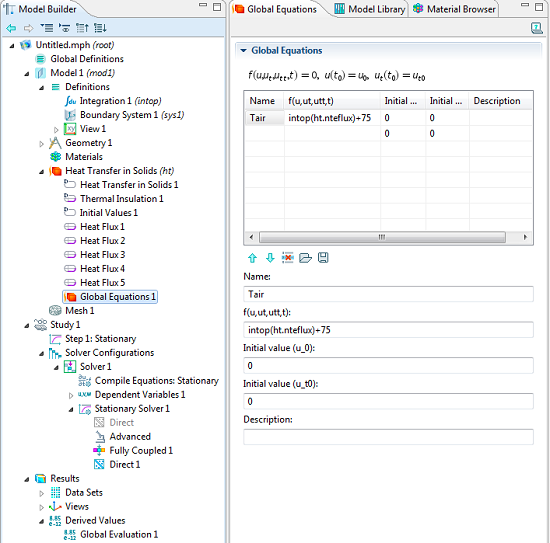
全局方程接口以及相应的求解器设置。
求解模型后,我们可以看到所有内壁的温度分布,并通过结果 > 派生值 > 全局计算对空气温度进行评估。我们假设空气温度均匀,从而简化了问题,并使用全局方程简化建模。这里展示的方法假定空气的热容量可以忽略不计,但如果我们想将它看作瞬态问题建模,可以将空气温度的时间导数以及空气的总质量和比热包含在全局方程中。
下一步
如果你想查看类似的示例,了解在模型中设置全局方程的所有步骤,请参阅使用全局方程满足约束条件案例教程。如果你认为使用全局方程对您的建模有所帮助,并有兴趣了解更多有关 COMSOL Multiphysics 的信息,请联系我们。



评论 (0)