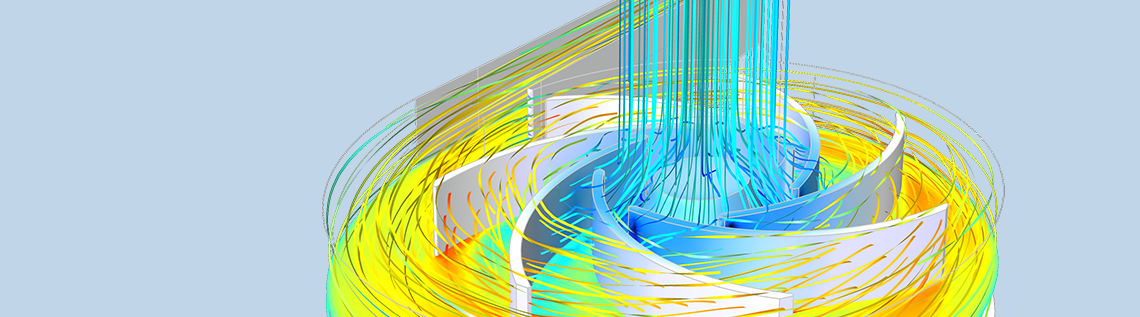
代数多重网格( algebraic multigrid,AMG)求解器提高大型 CFD 模型的计算效率。从 COMSOL Multiphysics 软件的 5.3a 版本开始,AMG 方法只需要一个网格,而几何多重网格(geometric multigrid,GMG)求解器至少需要一个额外的粗网格。这避免了为具有小细节的复杂几何图形创建粗网格的麻烦,除非使用精细网格,否则很难进行网格划分。
一个流体流动问题、数学模型和数值模型
流体流动可以用动量、质量和能量守恒定律来准确描述。描述这些定律最准确的方法是通过偏微分方程(PDEs)。描述这些规律的偏微分方程系统是非线性的。在大多数实际情况下,这些方程无法解析求解。但是我们可以在空间和时间上对偏微分方程进行离散化,以得到一个可以求解的代数方程的形式,进而获得偏微分方程的近似解。也就是说,用数值模型近似数学模型。
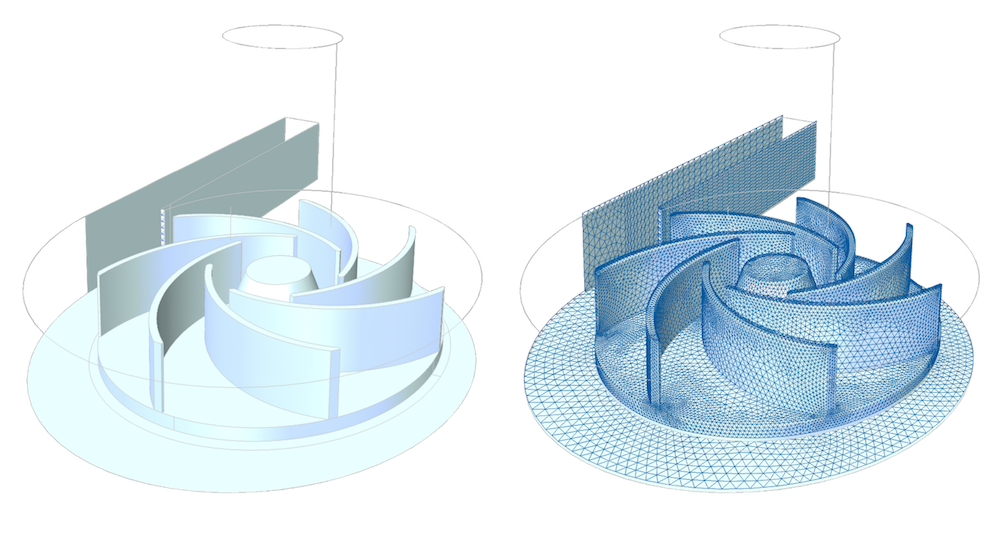
使用离散化描述近似左侧几何图形的“真实”描述。在离散化描述中,对每个单元进行了动量平衡和质量平衡。
对于空间和时间问题,COMSOL Multiphysics 使用线性方法,其中空间离散化使用有限元方法完成,时间离散化使用常微分方程的一些标准方法完成,例如向后微分公式(BDF)或广义 α。
流体流动方程是非线性的,这意味着离散化的数值模型方程也是非线性的。对于瞬态问题,必须在每个时间步求解一个非线性方程组。对于稳定流动,数值模型方程会形成一个必须求解一次的非线性方程组。
当系统完全耦合求解时,求解非线性方程组的方法,包括瞬态问题和稳态问题,都是用阻尼牛顿法。这种方法是基于非线性方程的线性化,并在一系列迭代中求解线性方程,通常称为牛顿迭代,直到我们获得所需的精度。
为什么我要对线性方程组使用迭代法?
在我们要将要讨论的案例中,有成千上万或数百万个方程与未知数与我们用来生成数值方程的有限元网格中的节点数量成比例。在每次牛顿迭代中,对于必须求解的线性方程系统,使用直接求解器求解代价很大。但是,我们可以用占更少内存的迭代求解器来求解线性方程。

即使是这个相对简单的离心泵流量模型,也需要350000个方程和未知数。感谢代数多重网格求解器,这些方程可以在台式电脑上求解。
对于流体流动问题,COMSOL Multiphysics 使用广义最小残差(generalized minimal residual,GMRES)方法求解,这是一种求解非常大的线性方程组的迭代方法。我们可以修改线性方程系统,使 GMRES 方法更好用。
多重网格方法
多重网格方法(Multigrid Methods)提供了一种优化技术,用于修改或预处理迭代技术(如 GMRES 方法)的方程系统。
几何多重网格方法适用于含不同级别网格的线性方程系统,从细网格到粗网格。它在对应于较粗和较细网格的不同线性系统之间传递候选解,即迭代。其思想是,直接方法仅针对最粗的网格求解,并且该信息可以更快地为更精细的网格找到解。粗网格问题需要小到不影响方法的性能。
在每次 GMRES 迭代中,几何多重网格 方法可以从更精细的网格开始,在那里可以获得系统的右侧,在称为预平滑的过程中将更精细的近似解映射到更粗的网格。使用直接求解器在最粗略的水平上修正方程的解。然后,在称为后平滑的过程中,这个解再次被映射到精细解。
对于每个 GMRES 迭代,可以重复上下网格级别的过程(V 循环)。当达到 GMRES 迭代中的容差时,我们就得到了线性系统足够好的解。
我为什么要使用代数多重网格方法?
几何多重网格方法对流体流动问题非常有效。但是,它有一个非常严重的局限性。对于复杂的几何图形,可能很难或几乎不可能生成一个粗糙的网格,这个网格需要给出的方程组足够小,可以在最粗糙的层次上求解。

离心泵的薄叶片导致叶片周围流体中的单元非常小。这也意味着,即使是最粗糙的网格也会产生太多的单元,从而产生太多的方程,因此无法用使用几何多重网格直接求解器来求解。
代数多重网格方法不需要不同的网格级别。代数多重网格方法中的粗化过程仅基于线性方程组的结构,或者更准确地说,基于表示方程组左侧的矩阵。该方法将矩阵中与其他元素连接较少的元素聚集成具有较小尺寸的新矩阵。聚集元素的过程可以重复,甚至可以构建更小的矩阵。然后,根据已执行的聚合次数为它们分配不同的级别。多重网格循环的原理与几何多重网格方法在不同层次上构造矩阵的原理相同。
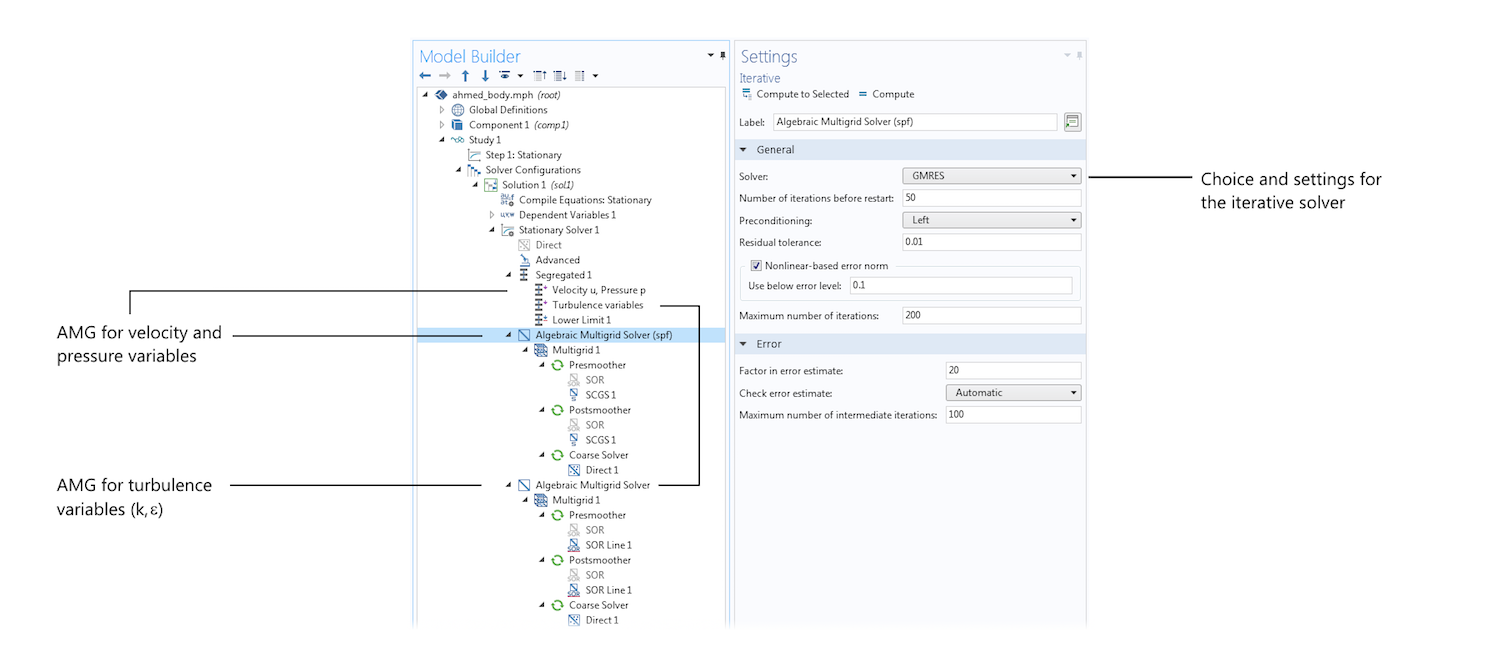
将迭代求解器(GMRES) 的设置与代数多重网格方法结合使用来求解如下所示的 Ahmed 体的模型方程。请注意,该方法用于在分离求解器的两个独立步骤中求解动量和连续性方程 (u, v, w, p) 以及湍流模型变量 (k, ε)。
求解器性能如何?
为了监控 COMSOL Multiphysics 中不同求解器设置的性能,每天要运行几千个测试。其中的一个迭代求解器和流体流动的测试案例是Ahmed体模型。另一种测试是层流静态混合器测试。测试结果表明,对于 630 万个自由度,代数多重网格方法在单核计算机上的求解时间比几何多重网格方法减少了约 13%。
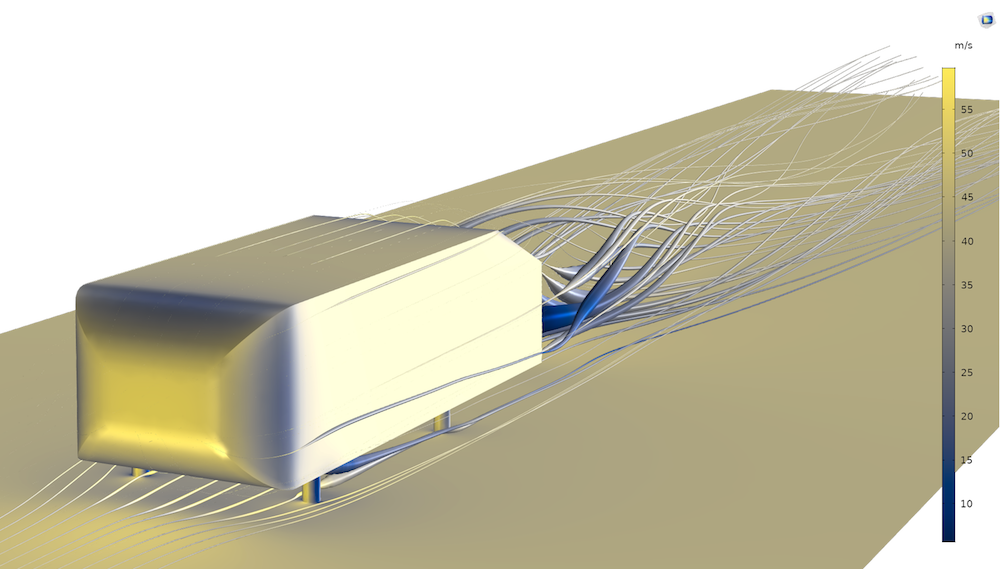
Ahmed 体是湍流的基准模型,也是一般湍流模型的验证模型。
请注意,这些结果反映了这些方法在 COMSOL Multiphysics 中的实现,而不是这些方法的一般属性。在一台有 4 个内核的计算机上,这一差异下降到 6% 左右。对于 32 核的计算机,两种方法的求解时间是相等的。出现这种情况的原因是几何多重网格求解器的并行化程度高于代数多重网格解算器。新的代数多重网格方法已经在第一年显示出其优越稳健性和卓越的性能,与几何多重网格方法的最佳情况相当。
后续步骤
通过下面的按钮,了解更多关于 COMSOL Multiphysics 的关键特性,以满足您的数值建模需求。
在 COMSOL 博客上阅读有关使用多重网格方法的更多信息:



评论 (0)