我应该选择哪种湍流模型求解 CFD 问题

针对湍流问题的求解，COMSOL Multiphysics^®提供了许多不同的公式，包括 L-VEL、algebraic yPlus、Spalart-Allmaras、k-ε、 k-ω、低雷诺数 k-ε、SST 以及 v2-f 湍流模型。所有这些公式都可以在 CFD 模块中调用，并且 L-VEL、 algebraic yPlus、k-ε 和低雷诺数 k-ε 公式还可以在传热模块中使用。阅读这篇博客，了解为什么要使用不同的湍流模型，如何从中进行选择，以及如何有效地使用它们。

这篇博客首次发布于 2013 年，现在已经更新，以反映从 COMSOL^®软件 5.3 版本开始 CFD 模块新增的所有湍流模型。

湍流模拟简介

考虑一块平板上的流体流动，如下图所示。均匀流体的速度分布接触到平板的前缘，开始形成一个层流边界层。这个区域的流体流动很容易预测。随着流体流过一段距离后，边界层内开始出现较小的紊乱振荡，流体流动逐渐过渡为湍流，最终变为完全湍流。

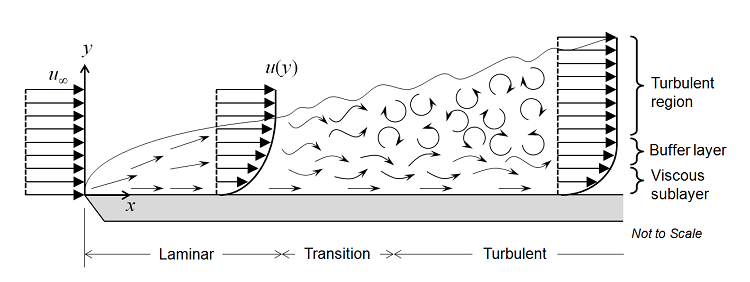
这三个区域之间的过渡可以用雷诺数Re=\rho v L/\mu来定义，其中\rho是流体密度，v为速度，L为特征长度（本例中为与到前缘的距离），\mu为流体的动态黏度。假设流体为牛顿流体，也就是说黏性张力与剪切速率成正比，动态黏度为比例常数。对于空气或水等各种具有工程应用价值的流体来说，这个假设是正确的。尽管这里假设流体为弱可压缩性，即马赫数小于0.3，密度仍然会随压力变化。COMSOL Multiphysics 的流体流动接口中的弱可压缩流动选项忽略了压力波对流场和压力场的影响。

在层流区，完全可以通过求解稳态Navier-Stokes 方程来预测流体流动，得到速度及压力分布。首先假定速度场不随时间变化，Blasius 边界层案例模型就是层流流动的典型示例。当流动开始过渡到湍流时，即使入口的流速不随时间变化，流动中也会出现紊乱振荡，因此无法再假定流动是稳态。在这种情况下，需要求解瞬态 Navier-Stokes 方程，所使用的网格也必须足够精细，才能解析流动中最小涡流的尺寸。例如，圆柱绕流案例模型中就对这种情况进行了演示。对于稳态和瞬态层流问题，仅使用 COMSOL Multiphysics 基本模块就可以求解，不需要任何附加产品。

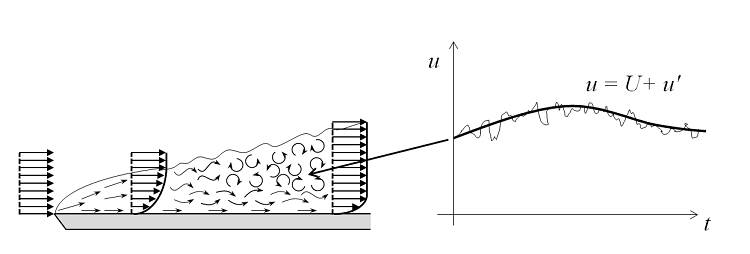
随着流速（以及雷诺数）的增加，流场中出现小涡流，振荡的空间和时间尺度变得非常短，因此不能再使用 Navier-Stokes 方程来求解这些问题。对于这种流型，我们可以基于以下观察：随着时间的变化，流场（u）中包含可以被处理为时间平均项 (U) 的局部小振荡 (u’)，此时可以使用雷诺平均 Navier-Stokes （RANS）方程来求解。对于一方程和两方程模型，通过引入额外的方程来包括湍流变量，例如湍流动能（k-ε 和 k-ω 公式中的 k）。

在代数模型中，为了描述湍流强度，我们引入了取决于速度场的代数方程（在某些情况下，还取决于与壁的距离）。然后，根据对湍流变量的估算，计算出增加流体分子黏度的涡流黏度。这样，原来由小涡流传递的动量被转化为黏性传递。除了靠近实体壁的黏性底层外，其他各处的湍流耗散都优于黏性耗散。因此，在湍流模型（例如低雷诺数模型）中，必须不断降低黏性底层的湍流水平。或者，必须使用壁函数来计算新的边界条件。

低雷诺数模型

“低雷诺数模型”听起来似乎与湍流流动的高雷诺数要求相悖，但这里的“低雷诺数”并非指全局范围内的流动，而是指黏性效应占主导的近壁区域，即上图中的黏性底层。当与壁的距离接近零时，低雷诺数模型可以准确地再现不同流动量的极限行为。因此，举例来说，当y→0 时，低雷诺数模型必定预测为k~y²。正确的极限行为意味着湍流模型可用于模拟整个边界层，包括黏性底层和缓冲层。

大多数基于 ω 的模型本质上都是低雷诺数模型。但是标准的 k-ε 模型和其他常见的 k-ε 模型不是低雷诺数模型。不过，其中一些模型可以通过补充阻尼函数来呈现正确的极限行为，这种模型被称为低雷诺数 k-ε 模型。

低雷诺数模型通常可以准确地描述边界层。然而，近壁的斜坡梯度较大，需要极高的网格分辨率，而高精度意味着计算成本高。这就是为什么在工业应用中常常使用替代方法来模拟近壁流动。

壁函数

近平板壁面处的湍流流动可被分为四个区域。在壁面处，流体速度为 0；对于紧邻壁面上方的薄层，流速和与离壁面的距离呈线性关系，这个区域被称为黏性底层，或层流底层。远离壁面的区域称作缓冲层。在缓冲区，湍流应力开始取代黏性应力成为主导，并最终过渡为完全湍流的区域，其中平均流速和与到壁面距离的对数呈线性关系。这个区域称为对数律层。在离壁面更远的区域，流动过渡为自由流动层。黏性底层和缓冲层非常薄，如果缓冲层到底部的距离为\delta，那么对数律层将延伸到距壁面大约100\delta远的地方。

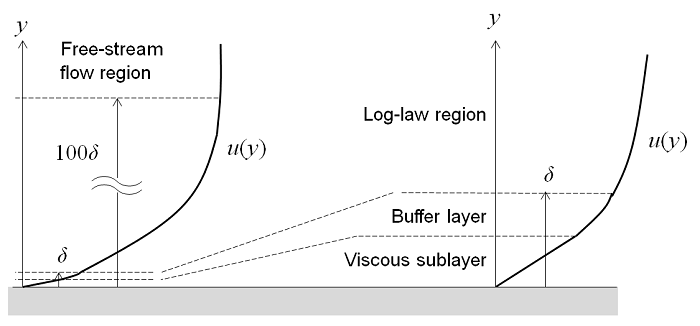
可以使用 RANS 模型计算所有四个区域中的流场。不过由于缓冲层非常薄，在该区域使用近似值更优优势。壁函数会忽略缓冲区内的流场，并计算壁面处非零流速的解析解。通过使用壁函数公式，可以为黏性层中的流动假设一个解析解，从而大幅降低计算量。对许多实际工程应用而言，这是一个非常实用的方法。

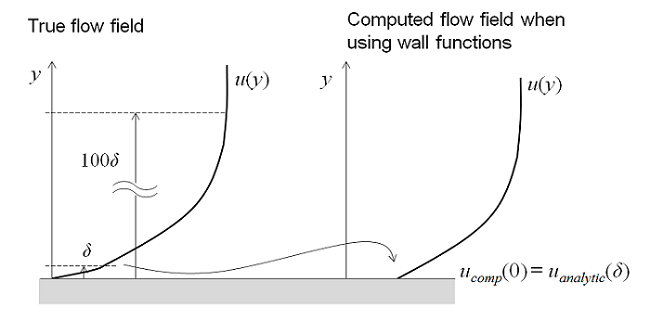
如果您所需的精度等级高于壁函数公式所能提供的等级，可以考虑能够求解整个流型的湍流模型（类似于上文中提到的低雷诺数模型）。例如，您可能希望计算一个对象上的升力和阻力，或者计算流体和壁面之间的热量传递。

自动壁处理功能

自动壁处理功能是自 COMSOL Multiphysics 5.3 版本开始推出的新功能，它不仅结合了壁函数和低雷诺数模型的优点，还可以根据模型中的网格自适应调整算法，同时获得解稳健性和准确性。例如，当边界层网格较粗时，该功能将利用稳健的壁函数公式。然而，当边界层网格较密，自动壁处理功能将采用低雷诺数公式将速度分布完全解析到壁面。

从低雷诺数公式到壁函数公式的过渡平滑自然。COMSOL 软件在边界单元中使用这两个公式的混合形式，首先计算出边界单元的网格点与壁面的距离（由升力得到的无量纲距离），然后将组合公式应用于边界条件。

除了 k-ε 模型外，COMSOL Multiphysics 中的所有湍流模型都支持自动壁处理功能。这表示低雷诺数模型也适用于工业应用，并且只有当网格足够精细时，才能调用它们的低雷诺数模拟功能。

各种湍流模型

接下来，我们将介绍 8 种湍流模型，这 8 种 RANS 湍流模型的区别在于，模拟近壁面的流动，求解的额外变量的数量及其物理意义时各有差异。 所有这些模型都在 Navier-Stokes 方程中增加了一个额外的湍流黏度项，但计算方法不同。

L-VEL 和 yPlus 模型

L-VEL 和 yPlus 代数湍流模型仅基于局部流速和到最近壁面的距离，使用代数表达式计算湍流黏度，不涉及求解额外的输运方程。这两模型能够求解整个流场，在所有 8 种模型中稳健性最好，计算量最少。虽然它们是精度最低的模型，但能很好地近似求解内部流动，尤其是在电子冷却应用中。

Spalart-Allmaras 模型

Spalart-Allmaras 模型增加了一个额外的无衰减动力涡黏粘度变量，它是一个低雷诺数模型，可求解实体壁内的整个流场。最初开发此模型是用于空气动力学应用，其优势在于相对稳健，且分辨率要求适中。根据经验，此模型不能精确计算剪切流、分离流或衰减湍流的流场，其优势在于稳健性和收敛性良好。

k-ε 模型

k-ε 模型求解了两个变量：湍流动能 k 和 湍流动能耗散率 ε。此模型使用了壁函数，因此不会模拟缓冲区中的流动。由于 k-ε 模型具有良好的收敛速度和相对较低的内存要求，因此在许多工业应用中都颇受欢迎，但它不能非常精确地计算逆压梯度和强曲率流动或射流流畅。此模型能够很好地求解复杂几何体周围的外部流动，例如，k-ε 模型可用于求解钝体周围的气流。

相较于 k-ε 模型，下面我们将介绍的湍流模型的非线性更强，除非提供良好的初始猜测值，否则它们往往很难收敛。k-ε 模型可以提供良好的初始猜测值，可以先使用 k-ε 模型求解模型，然后使用COMSOL Multiphysics 5.3 版本CFD 模块中的生成新的湍流接口功能。

k-ω 模型

k-ω 模型与 k-ε 模型类似，但它求解的是动能耗散的特定速率 ω。它是一个低雷诺数模型，但是可以与壁函数结合使用。它比 k-ε 模型的非线性更强，因此更难收敛，并且对于解的初始猜测值相当敏感。对于大多数 k-ε 模型求解精度较低的情况，比如内部流动、强曲率流动，分离流以及射流，k-ω 模型会非常有帮助。弯管头中的流动就是一个很好的内部流动示例。

低雷诺数 k-ε 模型

低雷诺数 k-ε 模型与 标准 k-ε 模型相似，但不需要壁函数：它能求解各处的流动，是对 k-ε 的合理扩展，拥有和后者一样的优势，但通常需要更密集的网格。它的低雷诺数属性不仅在壁面上，而且还在各处都起作用，从而抑制湍流。有时，建议首先使用 k-ε 模型计算出一个良好的初始条件，然后求解低雷诺数 k-ε 模型。另一种方法是使用自动壁处理功能，先利用粗化的边界层网格获取壁函数，然后对关注壁面处的边界层进行细化来获得低雷诺数模型。

低雷诺数 k-ε 模型可以计算升力和阻力，而且模拟热通量的精度远远大于 k-ε 模型。在大多数情况下，它能够很好的预测分离和再附着现象。

SST 模型

SST 模型结合了自由流中的 k-ε 和近壁 k-ω 模型，它是一个低雷诺数模型，是工业应用的“首选”模型。此模型与 k-ω 模型和低雷诺数模型具有相似的分辨率要求，但其公式消除了纯 k-ω 模型和 k-ε 模型的一些缺点。在一个案例模型中，SST 模型求解了NACA 0012机翼表面的流动，其计算结果与实验数据相吻合。

v2-f 模型

在接近壁面边界的位置，与垂直于壁面的方向相比，平行于壁面方向的速度波动通常要大得多，这种速度波动被认为是各向异性的。在距离壁面越远的地方，各个方向的波动大小相同，速度波动变为各向同性。

除了两个分别描述湍流动能（k）和耗散率（ε）的方程之外，v2-f 湍流模型使用了两个新方程来描述湍流边界层中湍流强度的各向异性。第一个方程描述了垂直于流线的湍流速度波动的传递过程。第二个方程解释了非局部效应，例如受壁面阻尼影响的垂直方向和平行方向之间的湍流动能再分布。

此模型适用于曲面上的封闭流动，例如模拟旋流器。

网格划分注意事项

求解任何一种流体流动，无论是层流还是湍流，计算量都很大。不仅需要相对较细的网格，还要求解许多变量。理想情况下，应该配备速度极快、内存高达数千字节的计算机来求解这类问题，即使这样，模拟大型三维模型仍可能要持续几小时甚至几天。因此，我们希望使用尽量简单，同时可以解析流动中所有细节的网格。

对于平板流动（以及大部分流动问题），速度场在壁面切线方向上的变化相当缓慢，但在垂直于壁面方向的变化相当迅速，尤其是考虑了缓冲层区域的情况。这一观察结果也促使我们使用边界层网格。边界层网格（使用物理场控制网格时，壁面默认使用的网格类型）会在壁面上插入二维薄矩形或三维三棱柱网格。纵横比较大的网格单元可以非常好地解析边界法向方向的流速变化，同时减少边界切线方向的计算点数量。

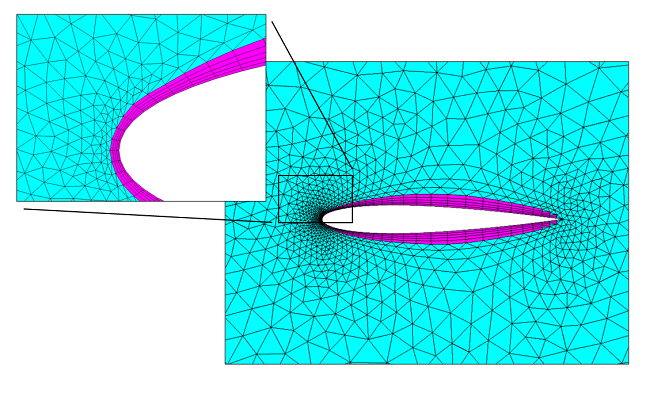
二维网格中绕机翼的边界层网格（紫红色），以及周围的三角形网格（青色）。

三维体网格中绕钝体的边界层网格（紫红色），以及周围的四面体网格（青色）。

湍流模型的计算结果

使用这些湍流模型求解流动模型后，您需要验证解是否准确。当然，与其他任何有限元模型一样，您可以简单地使用越来越细化的网格来重新运行该模型，并观察随着网格细化程度的增加，解的变化情况。一旦解在您可接受的范围内没有变化，那么可以认为模拟使用这些网格是收敛的。但在模拟湍流时，还需要检查一些额外的值。

使用壁函数公式时，您将需要检查无量纲壁分辨率（绘图默认生成）。通过该值来判断计算域从边界层的多远开始，且这个值不应该太大。如果壁分辨率超过了几百，则应该考虑在这些区域的壁面法向方向上的边界层网格需要进一步细化。在使用壁函数时，第二个要检查的变量是壁面升程（单位：长度）。该变量与假设的黏性层厚度有关，相对于几何体的外围尺寸应该较小。如果变量值较大，就应该对这些区域的网格进行细化处理。

无量纲最大壁面升程值小于 100，因此无需细化边界层网格。

使用自动壁处理功能求解低雷诺数模型时，应该检查到单元中心的无量纲距离（默认生成）。在代数模型中，此数值应该在所有位置都为同一量级，在两方程模型和 v2-f 模型中，此数值应小于 0.5。如果大于该数值，则应在这些区域细化网格。

结束语

在这篇博客中，我们讨论了 COMSOL Multiphysics 提供的各种湍流模型，重点介绍了什么时候使用，以及为什么要使用它们。COMSOL^®软件的真正优势在于模拟流体流动与其他物理场耦合的应用，例如，找到强风中太阳能电池板上的应力、模拟换热器中的强制对流，或者搅拌器中的质量传递等。

如果您对在计算流体力学 （CFD）和多物理场仿真中使用 COMSOL^®软件 感兴趣，或对本文尚未涉及的内容仍有疑问，欢迎联系我们。