壁附近的壁边界湍流梯度非常大。处理这些梯度的最准确方法是使用低雷诺数模型进行求解,但该模型的计算成本很高。工业应用中使用壁函数,即对最接近壁的流动进行建模,而不是对其进行求解。壁函数稳健而高效,但不是特别准确。COMSOL®软件中新增的自动壁处理功能结合了壁函数和低雷诺数模型的优点,可以高效而准确的计算这类问题。
自动壁处理的工作原理
COMSOL Multiphysics 5.3 版本中新增的自动壁处理功能将壁函数的稳健性与低雷诺数模型的精度相结合,根据模型中的网格采取相适应的公式。如果边界层网格较粗,则使用稳健的壁函数公式。如果边界层网格很密集,则使用低雷诺数公式,该公式可解析一直到壁的速度分布。
低雷诺数公式和壁函数公式之间的过渡是平滑的,并且是通过在边界网格混合使用两种公式来完成的。通过计算以黏性单位表示的边界单元网格点的壁面抬升距离,将两个公式组合用于边界条件。
下图是以黏性单位 y+ 为单位的壁距离与湍流耗散率 ε 的关系图,说明了低雷诺数公式和低雷诺数 k-ε 湍流模型的对数壁函数之间的过渡。绿色曲线代表 ε 的低雷诺数公式,蓝色曲线是壁函数表示,而红色曲线是用于自动壁处理的 Wolfshtein 模型。观察用 Wolfshtein 模型(红色)得到的平滑过渡,y+值范围为1到20,即处于缓冲层。
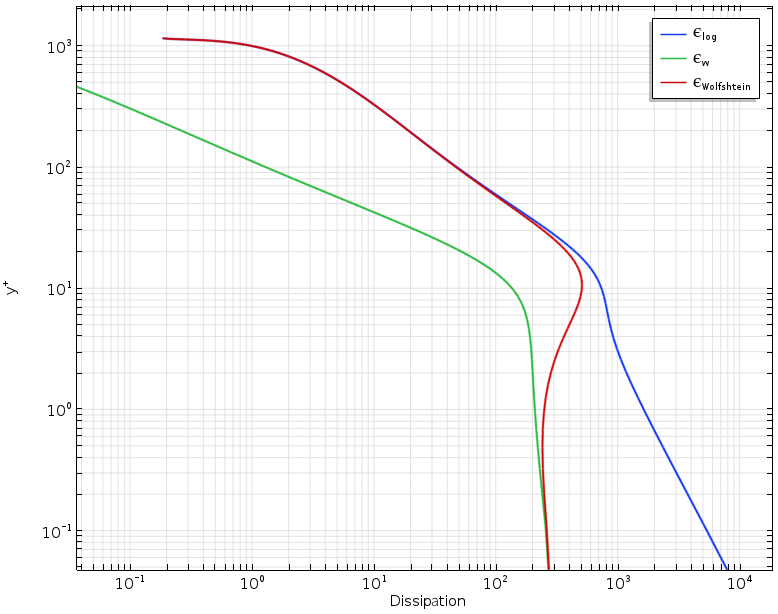
低雷诺数公式(绿色),壁函数(蓝色)和自动壁处理(红色)。
为了验证模型的定义,我们可以通过在边界处绘制 y+ 变量来研究如何处理壁,如下图所示。对于该管道弯头基准模型,可以看到在弯头的内曲面处,低雷诺数公式占主导地位,而在管道的直线段处,壁函数公式占主导地位。
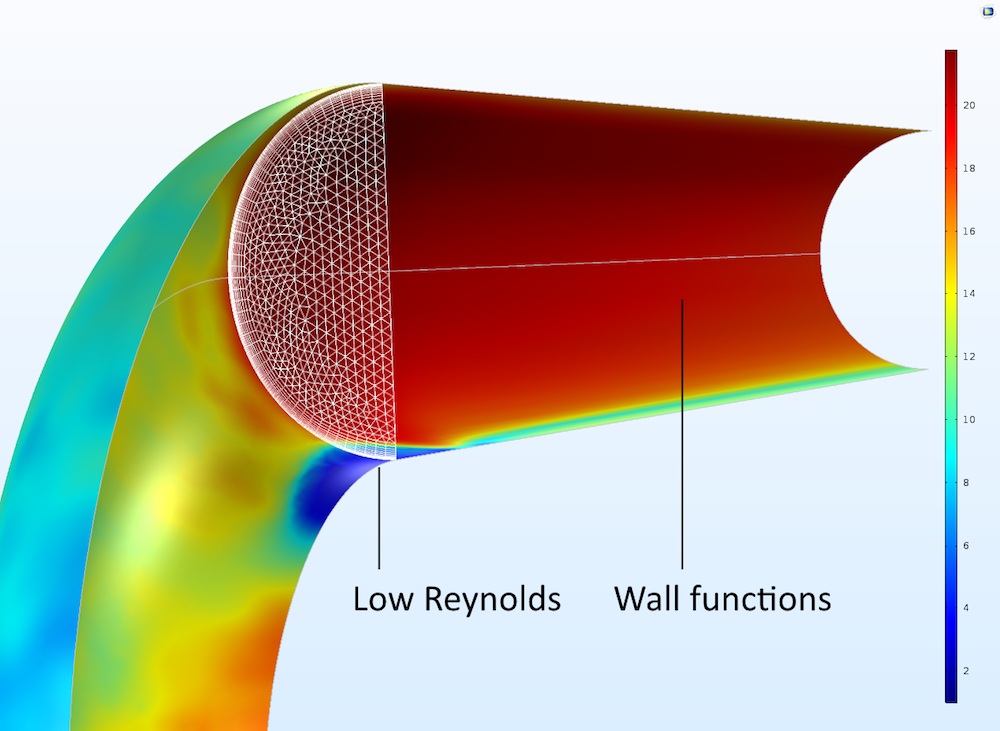
深红色区域的值为 y+,或大约 20,蓝色区域的值约为 1。
通过自动壁处理解决各种问题
自动壁处理功能允许使用低雷诺数模型处理更广泛的问题。例如,某些表面受到热通量、化学反应或流体-结构相互作用的耦合问题。我们可以只在需要精确解决边界层的相关表面上应用密集的网格(这可能在计算上非常昂贵),而不必在所有的表面上使用密集的网格。
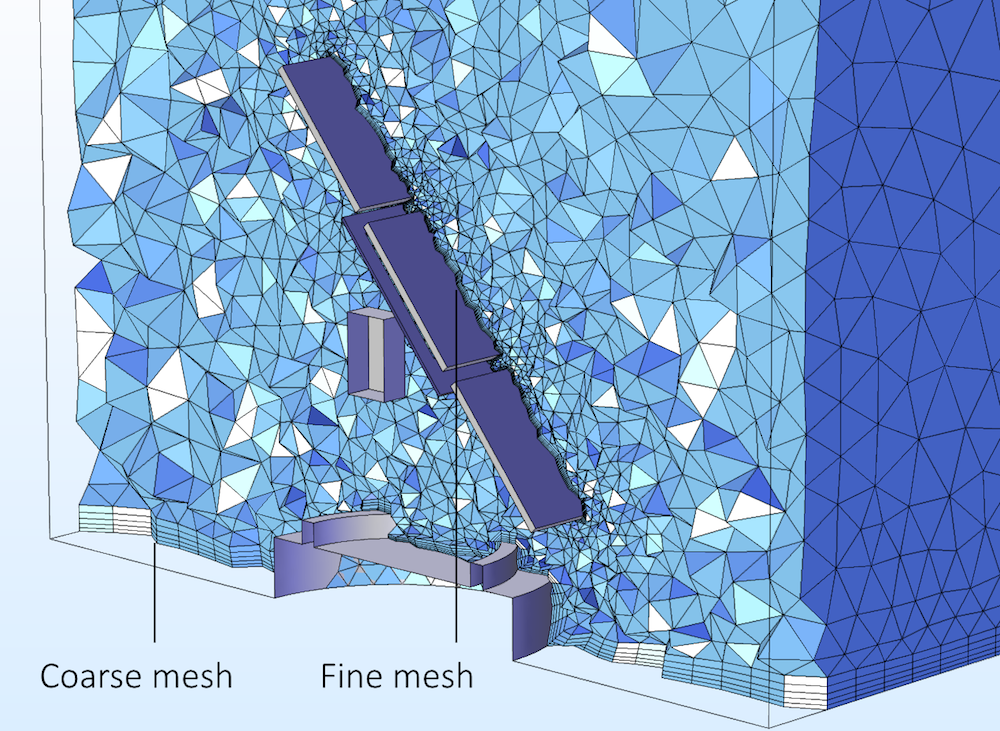
下图显示了 COMSOL 案例库中太阳能电池板模型的边界层网格。我们可以看到,电池面板表面的网格是密集的,具有紧密的边界单元。在这些表面上,我们需要高精度地计算流体对结构施加的力,用于计算应力和应变以及位移。混凝土基座不受风力的影响,这些表面上的力不需要相同的精度。使用自动壁处理功能,只需单击计算按钮就可以解决这个问题,而传统的低雷诺数模型需要在所有边界上设置密集的边界层网格才能收敛。
在这个太阳能电池板的流-固耦合教程中,我们可以对地面和混凝土基座使用粗边界层网格,在面板表面使用需要精确计算力的细网格。
简化模型开发
新功能在模型开发中也非常有用。为了弄清楚正确的假设和边界条件,第一步我们可能需要先使用粗网格,来快速获得结果。一旦验证了模型公式,就可以细化网格来获得更准确的结果。自动壁处理功能允许以最少的障碍和操作开发这种类型的模型:我们需要做的“唯一”事情就是细化网格。
这一新功能提供的稳健性还简化了低雷诺数湍流模型的一般使用。一个常见的过程是使用具有高雷诺数模型的壁函数求解模型方程,然后在低雷诺数模型中使用这个解作为起始猜测值。自适应壁处理将这个过程简化为粗网格和细网格的模型方程的顺序解;也就是说,它消除了首先创建和求解高雷诺数模型的需要。
湍流接口
自动壁处理可用于最新版本的 CFD 模块中的所有低雷诺数湍流模型接口:
- K-ω
- 低雷诺数 k-ε
- SST
- V2-f
- Spalart-Allmaras
- L-VEL
- 代数 y+
自动壁处理功能在上述所有流动接口的设置窗口中都可以使用。下图显示了选择湍流k-ω接口。在这个流动接口中,我们可以从三种不同的壁处理选项中进行选择:自动、壁函数和低雷诺数。
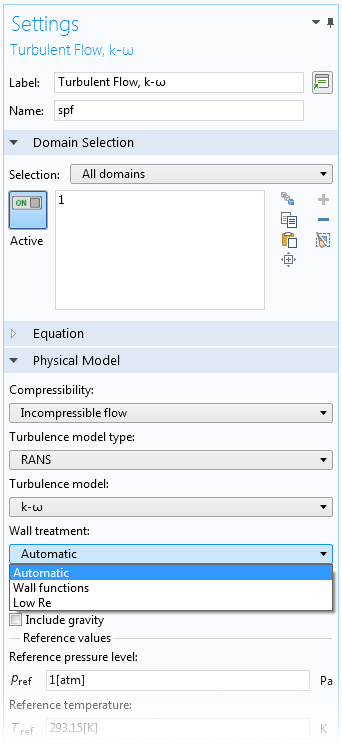
三个可用选项湍流,k-ω接口:自动、壁函数和低雷诺数。
更多资源
- 亲自动手尝试以下示例模型,了解自动壁处理功能的实际应用:




评论 (0)