在设计含有铁磁材料的磁性器件时,定义材料的磁属性尤为重要。不同材料(或者同种材料经过特定工艺加工)对相同刺激的反应各不相同,材料属性不合适可能会引起设备故障。COMSOL Multiphysics® 软件 5.2 版本扩展了当前对描述磁性材料的支持,允许通过外部常规程序来访问材料模型。在这里,我们将演示这一新功能如何应用于涉及磁滞的情况,并探讨当前模拟铁磁材料的可能性。
指定磁性模型的方法
在 COMSOL Multiphysics 中,所有推荐的公式中都包含大量可使用的域磁性材料对应的本构关系;例如磁场,无电流、磁场、磁场和电场和磁场公式。有时也可分别简写为 Vm 公式、A 公式、A-V 公式和 T 公式。
在接口中新增一个磁域时,默认情况下 COMSOL® 软件认为使用以下这个物理量即可完全描述:相对磁导率。由于相对磁导率非常接近 1,所以适用大部分抗磁性材料或顺磁性材料。对于软铁磁,可能仅定义相对磁导率就够了,只要输入一个较大的数值即可。如果磁导率的描述不够丰富,COMSOL Multiphysics 则提供了具体功能来直接定义:
- H-B 曲线或 B-H 曲线,其中数据制成查找表存储在材料中。AC/DC 模块中有 165 种材料已预加载了此类 B-H/H-B 曲线。
- 在考虑硬铁磁(即永磁体)和磁滞情况时,剩余磁通密度和磁化这两个功能就显得非常重要了。本篇博客文章中,我们将重点讨论磁化。
与相对磁导率类似,其他物理量可以任意定义,且与适当的动态模型相关联。例如,磁化可以关联为偏微分方程的解。Vector 矢量磁滞建模教程中的 Jiles-Atherton 磁滞实现中展示了这一点。
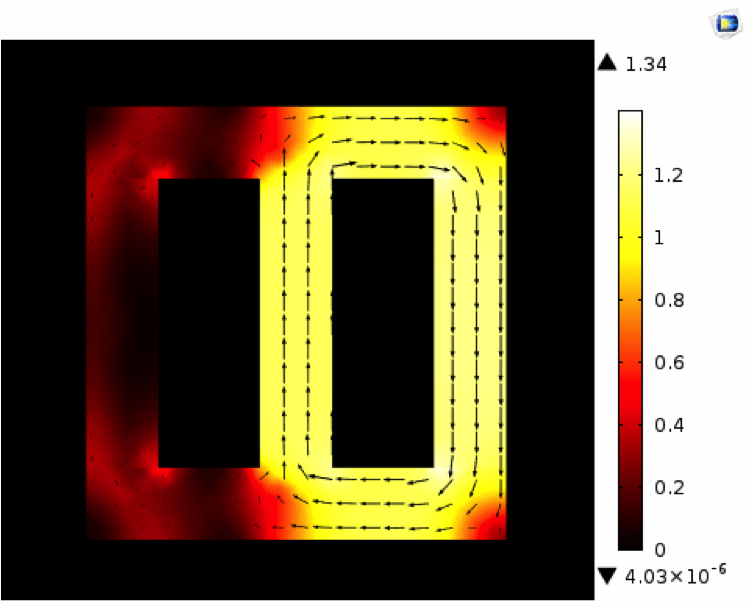
矢量磁滞建模教程中的磁通密度仿真结果。
假如材料模型包含非线性表达式,无法用标准变量或其他的偏微分方程来描述或描述相当困难,那该怎么办呢?COMSOL Multiphysics 5.2 版本的亮点之一是提供了一种指定外部材料磁性模型的新方法。该功能支持任何要耦合到电磁解的模型。让我们来一起了解一下这个功能…
新的外部材料用于定义材料模型
在 B-H 曲线和 H-B 曲线节点下,现在新增了一个选项用于将特定域的磁属性与外部材料相连接。在外部材料中,有两种指定磁性的实现方式:
- 广义 B(H) 关系
- 广义 H(B) 关系
第一个选项适用于磁场,无电流和磁场公式,第二个选项适用于磁场和磁场和电场。因此,COMSOL Multiphysics 对所有磁场接口都提供相同的支持。
之所以需要这两种不同的连接关系有几个原因。在磁场,无电流和磁场公式接口中,先计算因变量“磁场 H”。外部材料根据磁场的值输出磁通密度 B 的值。在磁场和磁场和电场接口中,则先计算因变量“磁通量 B”。因此,本构关系必须输出 H 作为 B 的函数。
在指定计算材料数据的公式时,COMSOL Multiphysics 会从指定为外部材料级别的共享库中调用原生函数。在 Windows® 操作系统中,该库就是一个动态链接库 (DLL)。
模型经适当编译后也可以在 Linux® 操作系统和 Mac OS X 上运行。
此操作就是编译 C 源代码的结果。该源代码可以包含 COMSOL Multiphysics 中定义的其他状态变量。包括磁化在内的这些状态变量使材料库和有限元模型之间进行通信。编码的动力学是任意的,所以每次迭代时,磁化、自洽磁场和磁通量遵循一个特定的磁滞模型而发生变化。
使用源代码的另一个优点是,可以更安全更方便地将模型分发给同事和客户。使用“App 开发器”甚至可以创建易于上手的包含外部材料函数的 App,使同事和客户都能查看结果。也可以自己保留材料模型的详细数据,如果有些磁性材料的详细数据属于限制级别,比如微磁学、纸币的磁性防伪油墨和军用设备消磁,使用包含这些材料的 App 是非常合适的。

一艘军舰在消磁码头进行消磁。
材料函数也可以用其他编程语言编写,因此可以方便地使用旧代码而不用 C 代码。
实践新功能
为展示新磁化功能的工作原理,我们在“案例下载”中新增了一个名为外部材料、AC/DC 模块、广义 H-B/B-H 关系的教程。该示例包含一个模型文件、一个 C 语言源文件以及一个共享动态链接库 (DLL),该库经编译可链接到64 位 Windows® 操作系统。此教程解释了,在使用 AC/DC 模块中的“软铁”材料作为 B-H 曲线的“来自材料”时,重现如何使用外部材料。
为解释可以在外部材料中定义的状态变量,我们将集中讨论以下具有磁滞效应和功能的情况:
- 外部材料状态变量 M, 表示局部磁化。
- 磁场,无电流公式。由此,外部材料计算磁通量 B 与磁场 H 和 M 的关系。在此例中,B = \mu_0(H + M)。
- 不使用代码难以指定磁化的动力学。
首先,我们讨论标量一维的情况,然后将示例扩展到一般的矢量三维的情况。一维中只需要磁化、磁场和磁通量的 x-分量。分别表示为 M、Hx 和 Bx。还需要找到最后收敛步骤中的磁化和磁场,分别表示为 oldHx 和 oldM。
磁化动力学 M 包括:
- 按比例随磁场变化的比例常数 xi。M = oldM + xi * (Hx – oldHx)。
- 磁化模量的最大值 Ms。如果 abs(M) > Ms,那么 M = Ms * sign(M)。
- 仅在材料未饱和,或材料饱和而局部磁通量与局部磁化方向相反时递减。
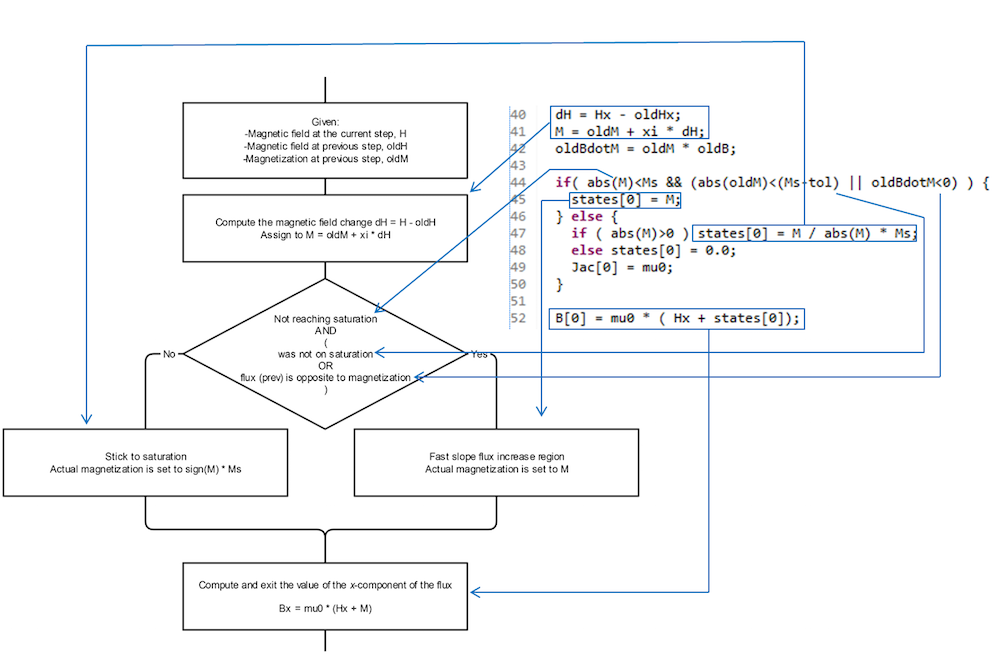
通过偏微分方程接口要实现这些动力学相当困难,尤其还存在条件语句的情况下。然而,如下图所示,只要按照几步简单的操作说明即可轻松实现。
该模型是非线性的,H 的结果值也许和 oldH 差别相当大,以致于一次迭代无法找到所有空间点都满足 Maxwell 方程的合适解。非线性收敛由标准的 COMSOL Multiphysics 求解引擎自动处理。对于快速而稳健的收敛,我们只需指定 \frac{\partial \text B_\text i }{\partial \text H_\text j}。这是一个 2 阶张量,其分量存储在变量 “Jac”(雅可比)中。对于目前的三维模型,它假定了一个非常简单的表达式,\text{ (1+xi)*}\mu_0\text * \delta_{ij}(非饱和时)以及 \text{ (1+xi)*}\mu_0\text * \delta_{ij}-\mu_0\text{*xi*}\frac{\text H_\text i\text H_\text j }{\text{(Ms)}^2}(饱和时),\delta_{ij} 是克罗内克函数。一维中只有雅可比矩阵的第一分量相当重要。其值为 \text{ (1+xi)*}\mu_0(非饱和时)以及 \mu_0(饱和时)。雅可比定义包含在标量一维和矢量三维代码中。
让我们来看一看该模型的部分结果。首先,考虑以下一维的情况,其中正弦均匀磁场施加于一个样本,这是一种最初未磁化的磁性材料。磁化结果类似下方绘图。
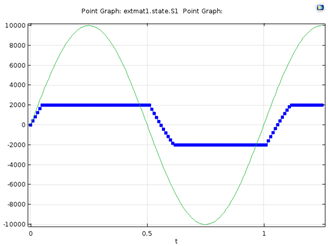
标量一维模型的结果。绿线表示外加磁场,带记号的蓝线表示磁化。
相应的磁通量则显示为下图中 B-H 平面上的轨迹。
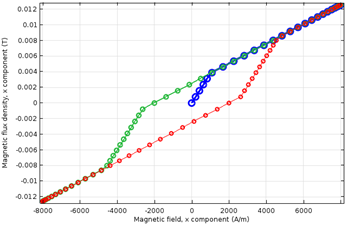
标量一维模型显示磁通量 B 的动力学与外加磁场 H 在一个正弦周期中的关系。起始点为原点,磁通量的动力学依次变为蓝线、绿线和红线。
第一次施加磁场时为蓝色曲线。此时,磁通量迅速增加达到磁化模量最大值 Ms,然后按照比例常数 \mu_0 缓慢增加。这是第一段磁化曲线。
当磁场由最大值降到最小值时,磁通量为绿色的下降曲线,这是磁滞曲线的上半段轨迹。该曲线的倾斜度发生了两次变化,一次是在上一个时间步的磁通量为负时,此时磁化方向反向(在到该点前磁化值一直增加,直到最大值 Ms)。在斜率变化较快的区域,磁化下降。倾斜度第二次变化发生在磁化达到 –Ms 时。接着,磁化停止,施加的磁场进一步下降使磁通量按比例常数 \mu_0 变化。
最后,当磁场再次上升到最大值时,磁通量为红色曲线,这是磁滞曲线的下半段轨迹。红线的轨迹与绿线相似。在红线上,倾斜度第一次变化对应磁通量变为正(磁化值为 –Ms,在该点之前磁化值一直增加,但为负)。在倾斜率第二次变化后,M = +Ms,红色曲线表示材料磁化到第一段磁化曲线终点这一运行点上。更多振幅相同的循环不断进行着先绿线后红线的重复。
尽管这个简化模型无法解释磁性材料的部分行为,但却能正确反映预期的磁滞。
注意,在绿色曲线上移动时,如果在倾斜率达到第二次变化之前磁场继续增加,则磁化也会开始继续增加。相应地,磁通量随着绿色曲线增加,但没有发生磁滞。如果不希望出现这种情况,则修改代码进行修正。
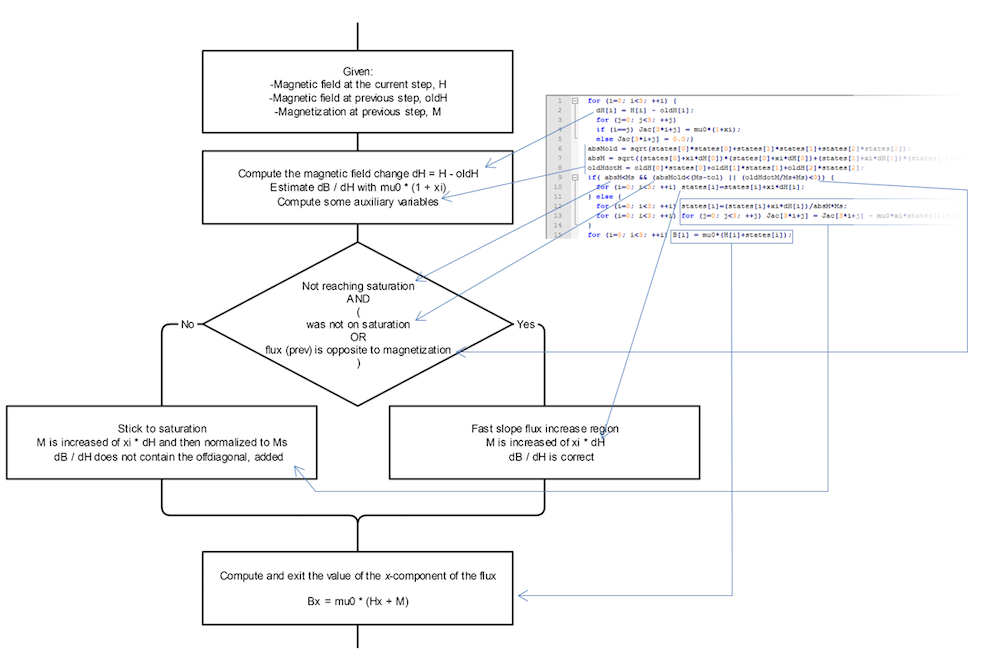
现在总结一下我们的观点以及上述模型中使用的代码,其中的磁化是一个遵循新流程图和代码的矢量。
代码只需编译一次即可用于一维、二维和三维。让我们先来看一个简单的二维模型。在这里,正方形使水平方向产生一个磁通量。正方形右侧是一个矩形样本,即上面描述的磁滞材料。下方绘图显示两种不同情景中发生的磁化。
磁性材料最初要么未磁化(左图),要么部分磁化(右图),外磁场先施加后移除。彩色点表示磁化的大小(和模量成正比)及颜色(表示方向)。彩色点上的黑色箭头和灰色箭头分别表示磁化和磁通量。
在以上两个场景中,颜色相同的区域表示磁化方向相似的域,突出显示磁化的矢量性质和磁域形成。尽管初始配置不同,但最终配置相似。
在下方绘图中,两种磁化模式在开始时完全相同,但脉冲之后差别很大。
现在,磁性材料在垂直方向已完全磁化,外磁场先施加后移除。右侧场景中的外磁场更强。
接下来,我们来看两个点的 B-H 关系。在下方绘图中,磁滞 B-H 曲线清晰可见。它们比之前的一维情况中光滑很多,部分原因是由于磁化可以旋转。
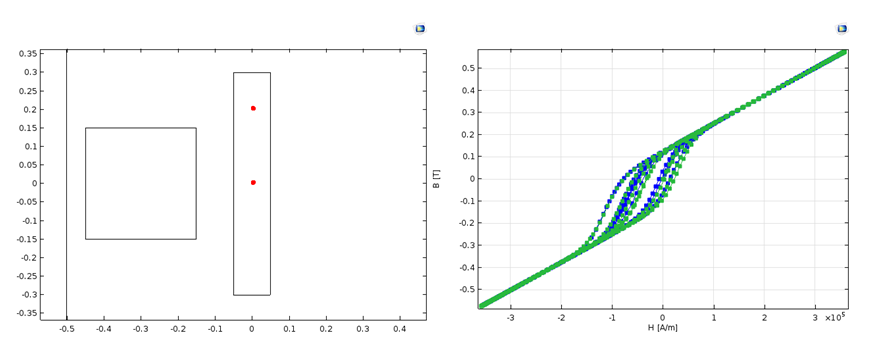
左图:两个具代表性点的位置。右图:绘图展示了低点的 B-H 曲线(x-分量)上, y-分量相似(蓝线),高点的 B-H 曲线( y-分量)上 x-分量相似(绿线)。
此流程适用于更常见的实例。为方便演示,我们在三维中使用相同的外部材料。在下方模型中,扳手下的线圈产生了一个磁脉冲。
注意,材料模型对应“广义 B(H)”关系。为创建此模型,将几何分拆成两个部分。线圈下部使用磁场公式。扳手上部使用磁场,无电流公式。在接触面上这两个磁场已适当耦合。

使用矢量磁滞模型的几何构型。
扳手由之前所述的外部磁性材料制成,且最初未磁化。线圈电流达到最大时,磁通量如下图所示。

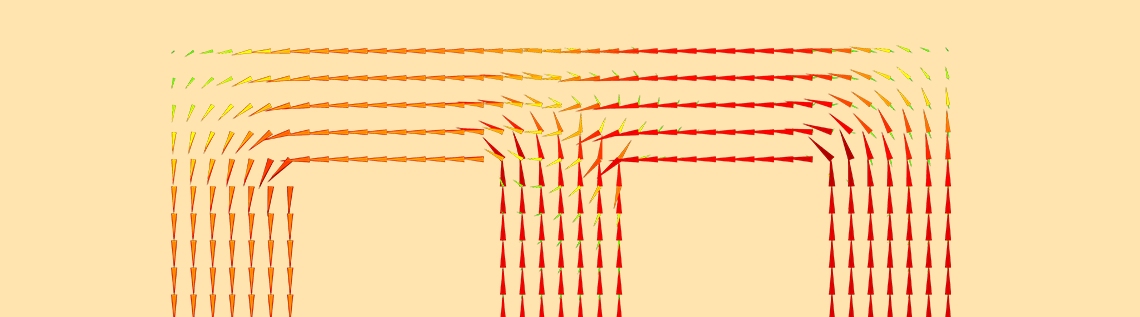
线圈电流达到最大时的磁通量。矢量长度表示磁通量(用对数刻度表示),颜色标尺为线性。
脉冲停止后,由于存在剩磁,扳手周围一直存在一些磁通量,如下图以及动画所示。
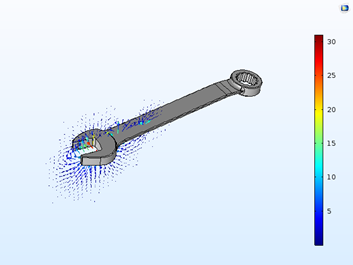
线圈电流消失后的磁通量。矢量长度表示磁通量(用对数刻度表示),颜色标尺为线性。
线圈产生电流脉冲时,磁化模量的动力学。
外部材料增强了磁性仿真
我们已了解到,使用新的外部材料模型,定义磁性材料时会多几个额外的选项且自由度更大。对于包括 Jiles-Atherton 和 Preisach 之类的经验模型,以及诸如微磁学中使用的基于能量最小化的模型,我们在这里展示的可以为实现类似不同模型带来一些启发。
有兴趣探索仿真中如何使用外部材料吗?
- 下载教程:外部材料、AC/DC 模块、广义 H-B/B-H 关系
- 如希望更详细地了解如何编译 C 代码用于不同的操作系统,欢迎阅读 COMSOL Multiphysics Reference Manual 中的 “Working with External Materials” 部分
- 有任何问题,请联系我们
Microsoft 和 Windows 是 Microsoft 公司在美国和/或其他国家或地区的注册商标或商标。
Linux 是 Linus Torvalds 的注册商标。
Mac OS 是 Apple 公司在美国或其他国家或地区的商标。


评论 (7)
国坤 陈
2016-11-22你好,怎么将外部材料赋给仿真的电磁材料,此外如何编写外部材料的模型
Yuansheng Zheng
2016-11-22陈国坤,您好!你可以下载文末的教学案例,根据博客的内容进行学习。您还可以参考以下博客:
//www.denkrieger.com/blogs/accessing-external-material-models-for-structural-mechanics/
智超 苏
2017-04-12您好,我发现文末的教学案例和博客内容并不相符啊,而且教学案例里的C文件里也没有博客截图中那些语句。而且如果选择了外部材料,在磁通量守恒里,就无法选择磁化,我的H不是通过线圈产生而是人为设置随时间变化。如果选择了外部材料,在磁通量守恒里,本构关系就是BH曲线,仿真过后,发现没有磁滞效果。我想请问一下,有没有用例?咱那个J-A磁滞的那个案例是有电流而且是各向异性材料,如果H自己设定、各向同性的材料怎么办?有相关案例吗?非常感谢!纠结了很久,真不知道该怎么办了
宇航 秦
2017-04-21苏智超,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:www.denkrieger.com/support
Email: support@comsol.com
谢谢!
梓 张
2018-10-24反磁性的物性怎么设置?
梓 张
2018-10-24您好,请问反磁性的物性怎么设置?
朗 朱
2019-04-26您好,请问能够提供扳手相关的模型吗