二维带电粒子束的相空间分布和发射度

在“束流物理中的相空间分布”系列博客中，我们介绍了概率分布函数（probability distribution function，简称 PDF）的含义，以及 COMSOL Multiphysics® 软件中的多种取样的方法。若要探究离子束和电子束是如何在真实环境中传播的，那么有关 PDF 的专业知识是必不可少的。在本篇文章中，我们将重点探讨相空间 和发射度 的概念，以及如何利用他们来描述束流离子或电子的释放问题。

离子束和电子束

离子或电子束 指的是动能几乎相同、沿近似同一方向运动的粒子组成的集群。通常情况下，每个粒子的总动能比常温下粒子的热能大得多，因此粒子束拥有极佳的方向性。

首先我们来观察带电粒子束的二维图像。我们用 z 轴正方向表示束流传播方向（轴向），用 x 轴表示与传播方向垂直的方向（横向）。虽然一开始您或许会觉得这种表示方式十分奇怪，但是请记住，我们最终的讨论目的是三维束流，到时候您就会发现用 x 和 y 轴表示两个横向方向将会带来很大的方便。

如上文所述，束流的特点在于它是由大量运动方向和能量都近似相同的粒子组成的集群——然而这里的重点正是“近似”！现实中任何束流中的粒子都不可能具有完全相同的速度。事实上，与束流的释放和传播相关的数学问题基本上都涉及到了束流粒子位置和速度的微小变化。

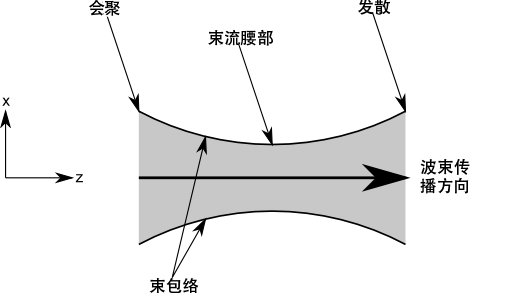
我们可以借助束包络 来表征束流形状，束包络指的是束流粒子的最外层，它能让我们了解束流的形状。如果束流存在一个锐减——即束流粒子的数密度在确定的位置上骤降为零——那么束包络或许只是一个曲线或包含所有粒子轨迹的表面。然而更常见的情况是，束流粒子的密度会在一个较大的距离内逐渐下降，因此束流终点和周围的空白空间并没有明确的界限。在这种情况下，束包络可以被定义为包含绝大部分发射粒子数的曲线或表面，通常包含 95% 左右。若束流的包络在传播方向上会逐渐变小，则此束流为会聚 束流；若包络随着束流的传播而变大，则为发散 束流。束流腰部 指的是束流刚刚结束会聚并即将开始发散时的位置。我们将在下文中对此进行详细介绍。

比较层束流和非层束流

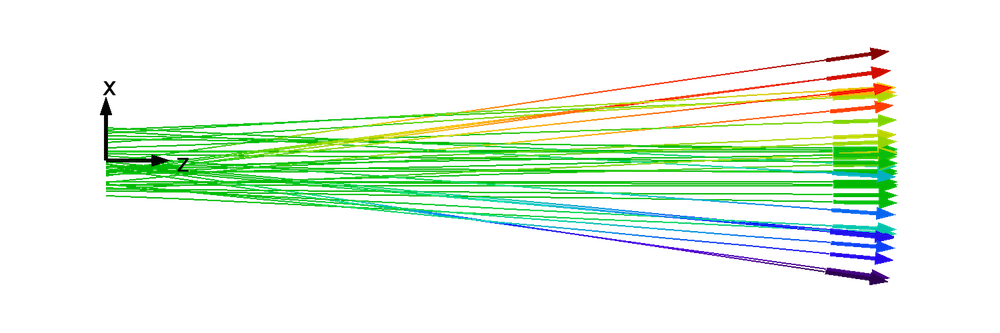
下图为一个简单的二维电子束，并描绘了其中具有代表性的粒子轨迹，模型暂时忽略了空间电荷效应及外力。坐标轴上添加了标签，以便指示轴向和横向。我们将它看成一个理想的带状电子束——也就是说，电子束在面外（y）方向上无限延伸。这些线指示了束流电子的路径，末端箭头表示各自的速度。每条线上的颜色表示电子在 x 坐标轴（或者说横向位置）上的变化，也称为横向位移。

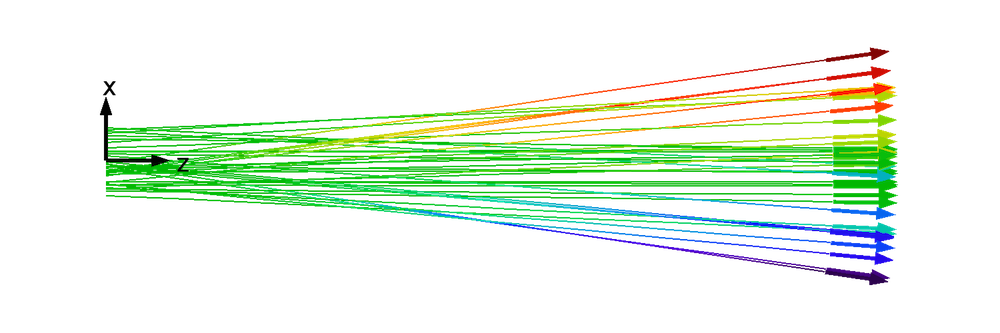
请注意，我们选定原点是为了使 x 轴的起始端位于电子束的中心。同时将中心线或标称轨迹 上的某一点作为起点，这会让横向粒子位置的测量变得十分容易。横向位置的变化率即横向速度 v_x。

从上图和后文的图片中我们可以看出，横向位移和横向速度相当夸张，十分容易观察到。但实际上，与沿电子束轴线的位移和速度相比，它们往往显得极其渺小。

由于具有下列属性，上图中的电子束被称为层束流：

1. 横向位置和速度之间存在一一对应的关系。在任意的横向位置上，电子束粒子的路径不会发生交叉。唯一的例外是会聚电子束，此类束流的全部粒子将交汇于同一点。
2. 横向位置和速度的比例关系是呈线性的。

第二个属性具有重要的意义，因为它保证了之后的过程不会被违背初始属性。在下方图示中，会聚电子束的横向位置和速度之间为平方关系，而非线性关系。初始时（z = 0）粒子轨迹无相交，但在后来某一点上发生了交叉。在图表中的任意一个交点上，一个横向位置可能对应着多个横向速度值，这与第一条属性是相悖的。

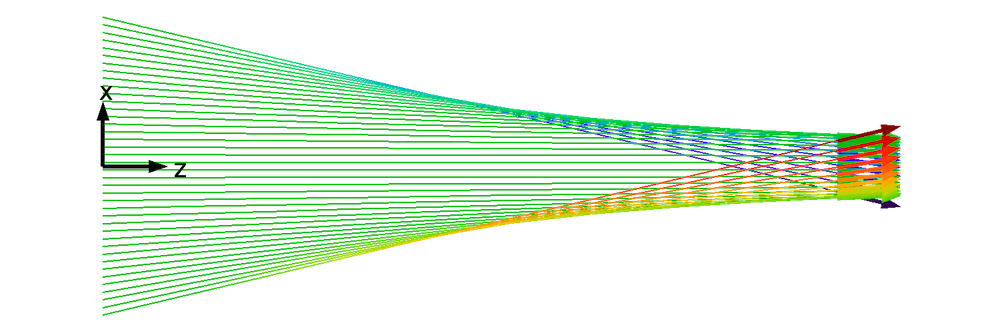
如下图所示，对于层流束而言，除非束流是会聚束流（所有轨迹相交于同一点），否则层束流的粒子永远也不会发生碰撞。

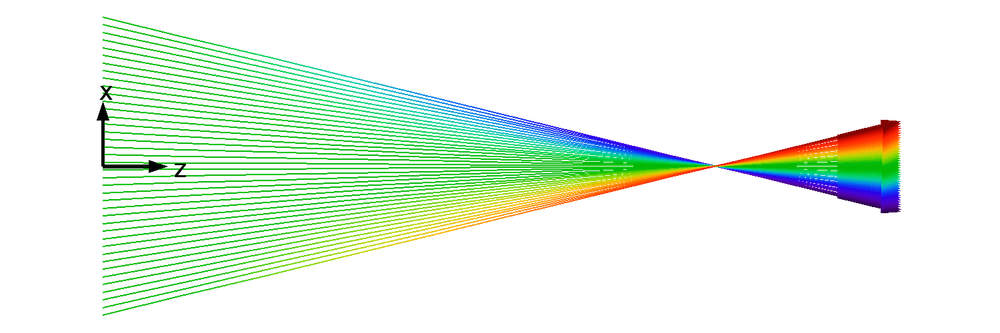
在真实环境中，任意一个横向位置都会存在具有横向速度的粒子分布，并且粒子轨迹之间会不断相互交叉，所以真实的粒子束均为非层束流，上文讨论的层束流只是一种理想情况。下图显示了一种更贴近现实的非层束流的横向速度分布情况。

接下来，为了更好地理解层束流和非层束流之间的差异，我们来观察一下二者的相空间分布。相空间分布具有多种形式，不过在本文中，我们只需要将粒子作为二维空间中的分布的点来进行研究，其中两条坐标轴分别表示横向位置和速度。当然，我们也可以将位置和动量用作坐标轴，这样做虽然会影响分布区域，但不会从根本上改变其形状。借助相图 绘图类型，我们可以很方便地在 COMSOL Multiphysics 中绘制上述的相空间分布状况。

首先，让我们观察一下层束流的相图。下图显示了时间 t = 0 时，一条释放边界上的分布情况。

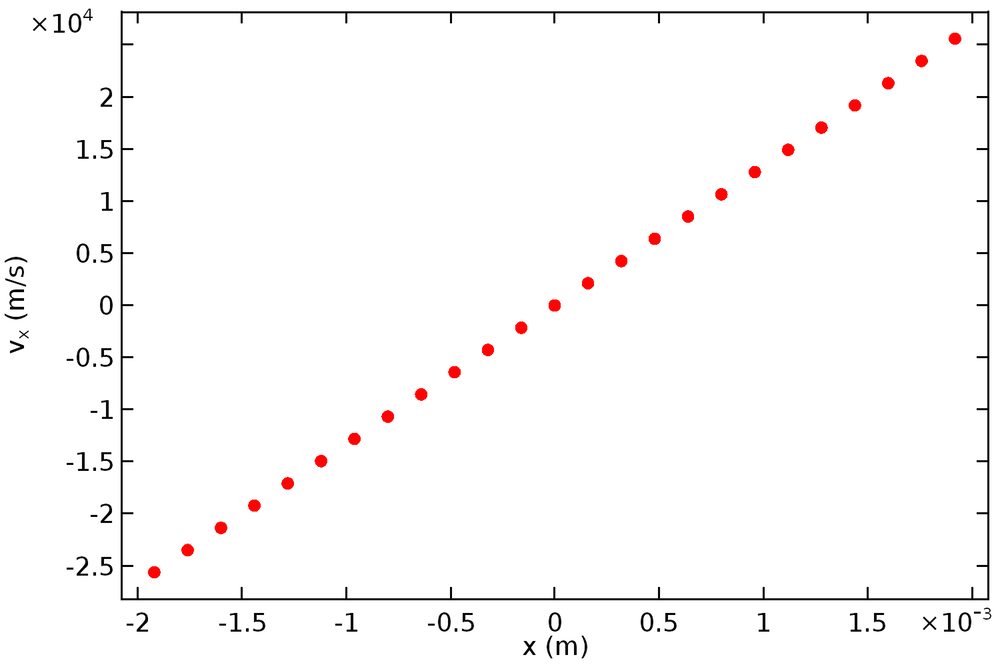
正如我们所料，边界上的点形成了一条穿过原点的直线。（请记住，按照定义，层束流中粒子的横向位置和速度之间存在一种线性关系。）下图为非层束流的相图。

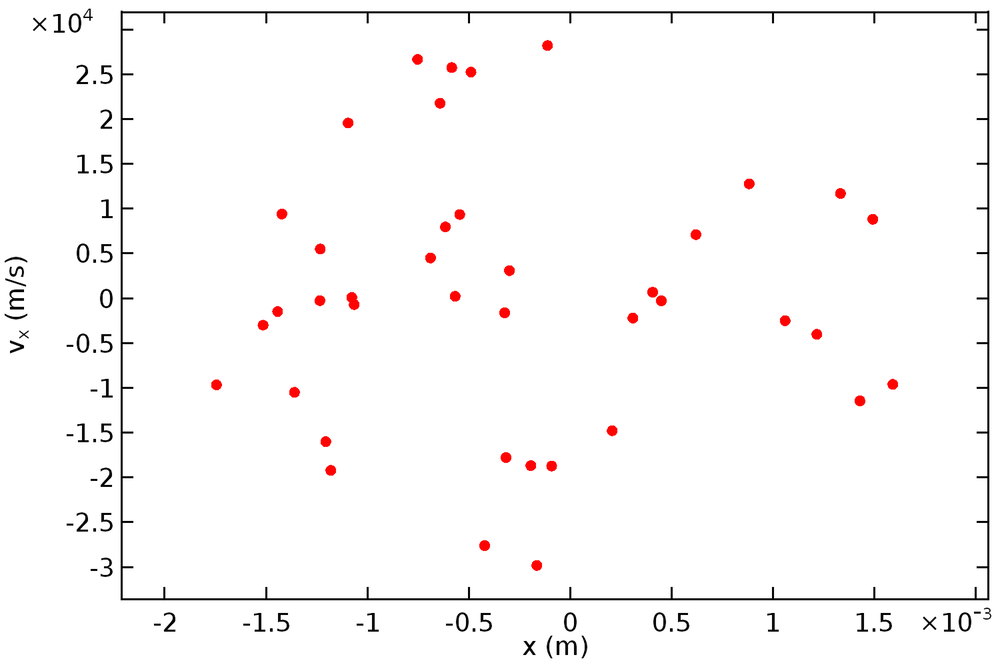
这些点不再位于同一条直线上，而是在以原点为中心的相空间中形成了一片边界模糊不清的云。这些点看似分布随机，位置并不存在任何明显的位置关联。为了更加清楚地了解相位空间分布，我们将此电子束的样本量大幅扩充到了 1000 颗粒子。

现在，我们得到了一张更加清晰的图像：粒子形成了一个相空间椭圆。椭圆中心的粒子最为密集，这说明与靠近束包络边缘的粒子相比，靠近电子束轴线的粒子速度分布范围更广。在束流物理中，这一类椭圆形的分布极其常见，不过在其他情况中，椭圆的比例和取向会发生变化，粒子具体位置也会相应地改变。与束包络的描述一样，相空间椭圆的数密度要么存在一个锐减，要么逐渐下降。在后一种情况中，我们可以对椭圆进行定义，使其包含特定比例的束流粒子，例如 95%。

在真实环境中，多数带电粒子束为近轴，这意味着与纵向速度相比，横向的速度分量非常小。在近轴极限处，我们可以使用粒子的横向位置 x 和倾角 x' = v_x/v_z 对其进行描述。之所以可以将后者看为角，是因为 sin(x') \approx x' 受近轴条件限制。束流粒子的 x 和 x’ 值的分布即迹空间分布，包含该分布的椭圆便是迹空间椭圆。

相空间椭圆的演化过程

上图中的椭圆关于 x 轴和 v_x 轴近似对称。然而，这种情况不会一直持续下去；粒子束传播时，即使没有施加任何力，椭圆形状也会改变，这只是因为沿两条坐标轴的表达式是相互关联的。根据定义 dx/dt=v_x，横向速度值为正（v_x > 0）的粒子在相空间中向右移动（x 轴正方向）；同样地，横向速度值为负的粒子将向左移动。下图中的动画演示了当不考虑空间电荷效应时，漂移粒子束的相空间椭圆随时间的演化状况。

若椭圆关于 x 轴和 v_x 轴镜面对称，我们便称此椭圆为直立 的。直立的相空间椭圆对应的是束流轨迹上的束流腰部。

束流发射度简介

在束流物理场中，更为方便的做法是在迹空间（x-x’ 平面）中处理问题，而非在 x-v_x 平面或 x-p_x 平面中。一部分原因在于，与横向速度或动量相比，借助倾角 x’ 对束流形状进行可视化能获取更加实用的效果。迹空间椭圆（即位于 x-x’ 平面内且包含迹空间粒子的椭圆）的通式如下

其中，参数 γ、β 及 α 被称为 Twiss 参数 或 Courant-Snyder 参数，它们都不是独立的参数，而是共同构成了 Courant-Snyder 条件，

(1)

物理量 \gamma \beta -\alpha^2 也被称为 Courant-Snyder 不变量。

参数 γ、β、α 及 ε 可用于描述迹空间椭圆的形状、尺寸和取向，具体方式如下：

• 相对于方程（1）使用的其他参数而言，γ 是最常用的的参数，它用于描述束流的比例。ε 恒定不变，γ 增加时，束流占据的空间区域将随之减小（x 值范围缩小），与此同时速度分布随之增大（x’ 值范围扩大）。
• α 用于描述迹空间椭圆的倾斜度。在直立椭圆中，α 对应的是束流腰部，且 α = 0。若 α > 0，则为会聚束流；若 α < 0，则为发散束流。
• β 也被称为振幅函数 或电子感应加速函数，用于描述束流的比例。ε 恒定不变，β 增加时，束流占据的空间区域将随之增大（x 值范围扩大），与此同时速度分布随之减小（x’ 值范围缩小）。
• ε 用于描述迹空间椭圆的大小，又被称为发射度。因为我们正在讨论横向位置和动量，所以将其称为横向发射度 会更加形象具体。

虽然束流发射度能够描述椭圆的大小，但对于发射度和椭圆面积之间的实际关系，存在多个不同的描述方式。其中一种方式是使用椭圆的长半轴长度和短半轴长度的乘积来表示发射度，此时 A = 4πε。下方图表便使用了这一方式，同时还进一步演示了 Twiss 参数是如何影响椭圆的比例和取向的。

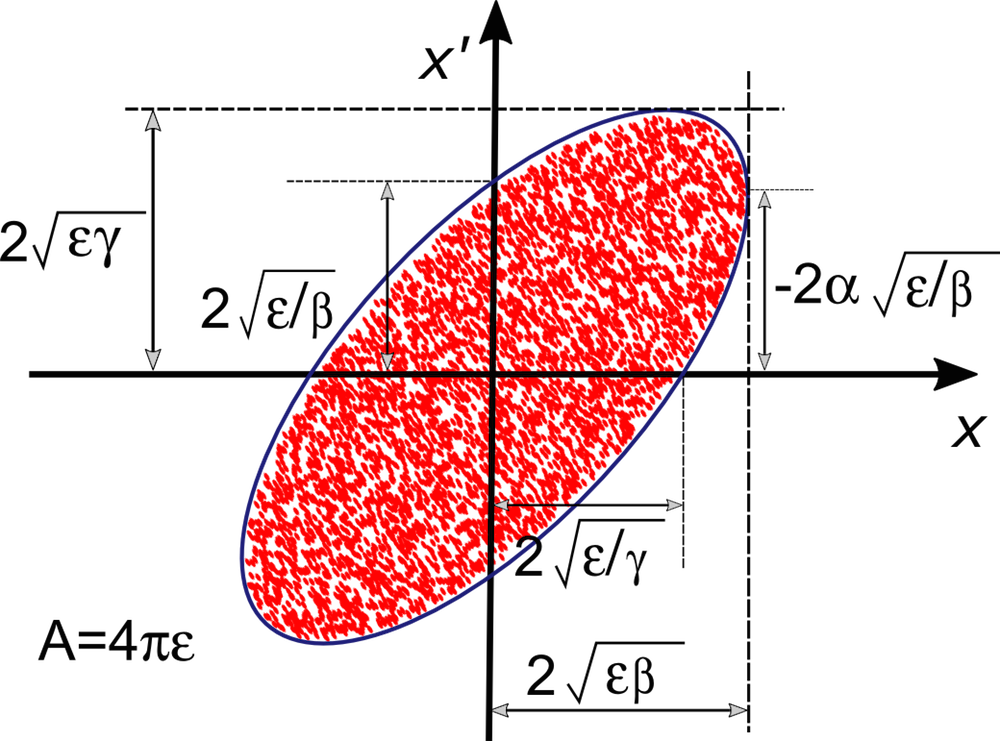
将上述的发射度乘以 4 是一种极其常见的做法，此时 A = πε。一些文献中还会将发射度除以 π，使 A = ε，这一步骤通常并不会特别说明。综上所述，在输入或阅读束流发射度记录时，我们必须确保自己了解使用的是哪一种方式。

从统计学角度解释发射度

到目前为止，我们已经确认了束流发射度的大小代表着被束流覆盖的相空间面积。除了从几何角度解释之外，我们还可以从统计学角度进行解释，即使用全部粒子的平均值来描述发射度。

均方根发射度（或 RMS 发射度）可以被定义为

(2)

其中尖括号代表的是算术平均，即

在发射度的几何定义中，人们往往将 RMS 发射度的表达式乘以 4：

(3)

在 COMSOL Multiphysics 中，为了明确定义发射度，我们采取了额外的预防措施：将方程（2）称为 1-rms 发射度，并将方程（3）称为 4-rms 发射度。如果迹空间椭圆的中心与 x-x’ 平面的原点重合，则 (x) = (x') = 0，并且方程（2）可以简化为

其中，方程左侧的项带有下标，是为了更清楚地表明它是 1-rms 发射度。同样地，Twiss 参数的统计定义可以写成（再次使用了简化假设 (x) = (x') = 0）：

由 Twiss 参数的统计定义可以明确看出：当大部分粒子位于迹空间的第二象限和第四象限时，则 α 为正，这说明束流正在会聚。

从统计学角度解释束流发射度还有一个好处：为了确定不规则相空间分布的面积，我们要围绕它绘制一个椭圆，但椭圆会带来一定的模糊性，而统计解释可以消除这种模糊性。同时这种方法也有一个缺点，那就是如果不存在明显的截断距离，远离束流中心的少量粒子会给发射度和 Twiss 参数出现明显的偏差。有时，这些粒子被刻意排除在束流发射度的统计定义之外，例如高斯分布“尾巴”上的粒子。

有关束流发射度的讨论

较小的束流发射度数值，通常与以下束流属性有关：

• 束流尺寸较小（x 值范围减小）
• 速度分布较窄（x’ 值范围减小）

人们通常希望尽可能地降低束流发射度。然而，在大多数情况下，束流发射度要么为恒定不变，要么还会增加。目前已有多种技术可实现束流冷却 或者发射度降低，但本系列博客不会对束流冷却技术进行深入的探讨。

为什么我们要如此关注如何降低发射度的问题？排除其他原因不谈，我们一定还记得粒子物理学的基础研究极大地推动了粒子加速器的发展，尤其是在高能物理应用领域。为了让粒子在极高的能量条件下发生碰撞，一定要保证两束粒子相交，而不是让粒子束与静止目标相交。但是，对于两条相交的束流，其碰撞截面远小于一条束流与静止目标相交时的碰撞截面。

出于上述原因，现代粒子加速器的技术目标便是使尽可能多的高能粒子进入一个狭窄空间，从而最大限度地提高碰撞概率。发射度较高意味着粒子扩散的区域面积较大或粒子速度的差异较大，后者会导致粒子占据较宽阔的区域。无论是哪个原因，都不利于提高交叉束流之间的碰撞频率。

扩展到三维环境

到目前为止，我们探讨了什么是粒子束、如何区分层束流和非层束流，以及非层束流的相空间分布是如何与横向发射度的概念联系在一起的。我们还了解到，真实的束流通常在相空间或迹空间中占据有限尺寸的区域，同时其发射度是一个品质因数，且通常在某种程度上与相空间的面积成正比。此外，我们还探讨了束流发射度的两种解释方式：相空间区域内的几何法和以束流粒子的平均值及其倾角进行表示的统计法。

本文仅对理想的二维带状电子束进行了讨论。当扩展到三维时，我们需要考虑两个正交横向上的发射度。真实的束流在轴向上也有一定的速度分布，因此会产生纵向发射度。

在下一篇博客文章中，我们将首次对三维粒子束中的相空间分布进行研究，并学习如何从相空间分布取样，以便对目前为止我们观察到的相空间椭圆进行重现。

了解更多使用 COMSOL Multiphysics® 模拟粒子追踪的内容

• 查看束流物理中相空间分布系列的全部博客文章
• 浏览“COMSOL 博客”，查阅更多关于粒子追踪模拟的博客文章

参考文献

1. Humphries, Stanley. Charged Particle Beams. Courier Corporation, 2013.
2. Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.