本系列博客将深入探讨粒子追踪技术在离子束和电子束仿真中的应用。我们首先会介绍概率分布函数(probability distribution function,简称 PDF)的背景知识,并展示在 COMSOL Multiphysics® 软件中对其进行随机抽样的多种方法。在后续文章中,我们还将演示如何基于该数学理论来精准地模拟真实环境中离子束和电子束的传播。
使用概率分布函数的目的
带有能量的离子束和电子束是高能物理和核物理基础研究领域的热门话题,它们也被广泛应用于阴极射线管,医用同位素的生产和核废料处理等领域。对于光束传播的精确数值仿真而言,粒子位置和速度分量的初始值是十分重要的参数。
在粒子追踪仿真中,当释放束流离子或电子时,通常情况下我们需要抽样选取部分粒子作为相空间 中的离散点。不过,在深入探讨什么是相空间,以及离子或电子如何形成相空间之前,我们先来大致了解一下概率分布函数以及如何在 COMSOL Multiphysics 中使用。
概率分布函数简介
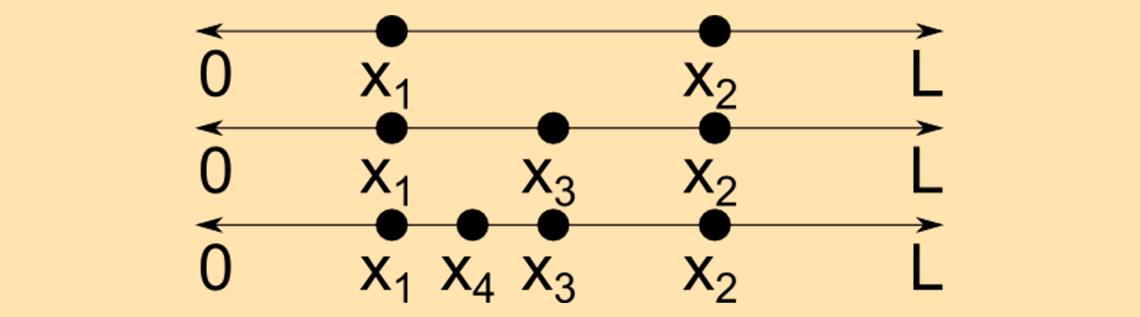
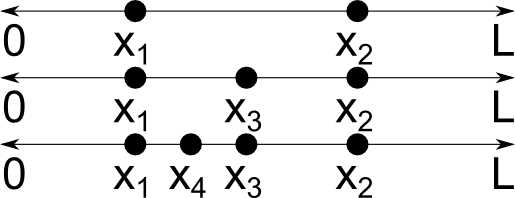
首先,我们对相关物理量进行定义。连续随机变量 x 是一个可以取无穷多值的随机变量。举例来说,假设在长度为 L 的线段上随机选择点 x1,在线段的另一处选择第二个点 x2。假设这两点是不同的点,我们便可以在该线段上选择第三个不同点 x_3 = (x_1+x_2)/2,然后是第四个点 x_4 = (x_1+x_3)/2,以此类推,从而获得无限多个不同的点,如下所示。
值得一提的是,另一种随机变量被称为离散随机变量,它只能取特定的值。想象你在投掷硬币或从扑克中抽取一张纸牌,这时结果的数量是有限的。
一维概率分布函数 f(x) 又称概率密度函数,主要用于描述连续随机变量的值等于给定值的概率。例如下方的概率分布函数
(1)
\begin{array}{cc}
0 & x\leq 0\\
1 & 0 \textless x \textless 1\\
0 & 1\leq x
\end{array}
\right.
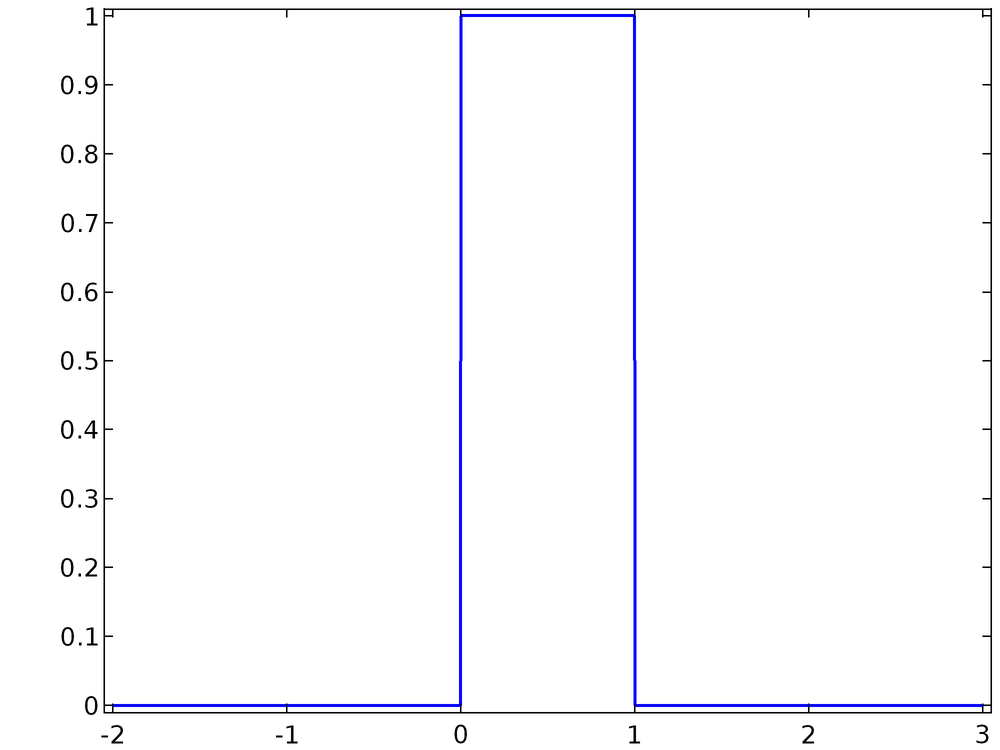
对变量 x 进行了描述,该变量在开区间(0,1)内取任意值的概率是均等的,但不会在区间外取值。此 PDF 是均匀分布,其绘图如下所示。
概率分布函数同样可以用于离散随机变量,甚至适用于在某些区间内为连续、在其他区间内为离散的变量。后一类随机变量还可以被当作连续随机变量进行解释,只不过它的 PDF 包含了一个或多个狄拉克δ函数。本系列博客仅讨论连续型随机变量。
若满足以下条件,则 PDF 会被归一化
换句话说,变量 x 在范围 (-∞, ∞) 内取任意值的总概率为 1。
累积分布函数(cumulative distribution function,简称 CDF) F(x) 指连续随机变量的值出现在区间 (-∞, x) 内的概率。CDF 是 PDF 的积分,表示为
上述定义清楚地表明,如果概率分布函数被归一化,则
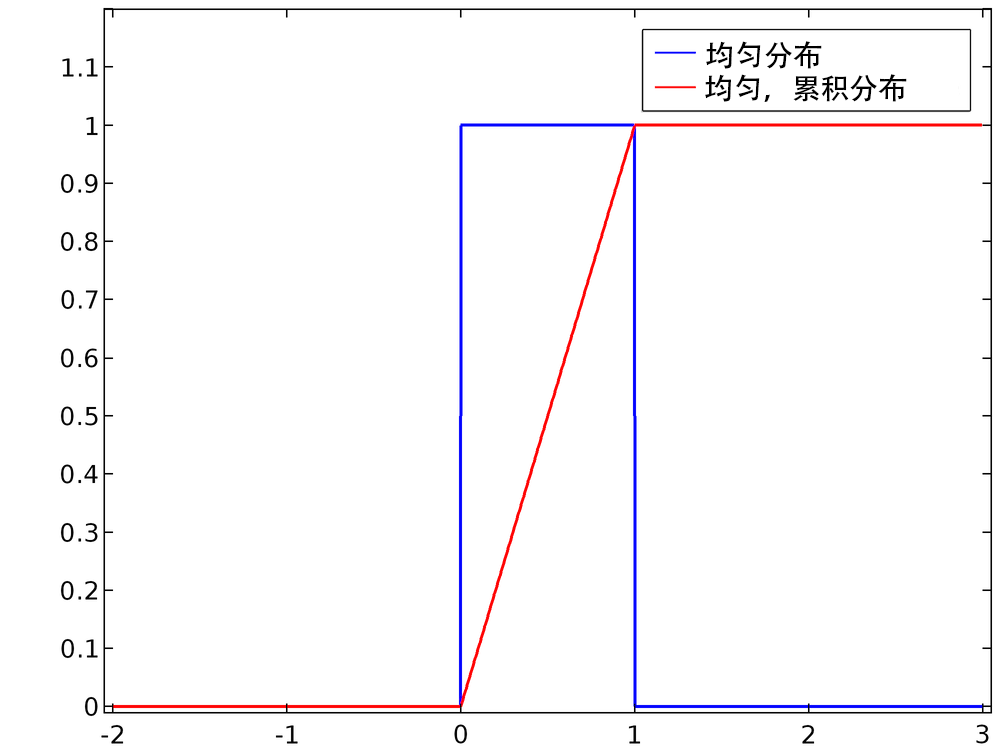
方程(1)的 PDF 及其对应的 CDF 见下方图表。很明显,PDF已经被归一化了。
从一维分布中抽样
从均匀分布中随机取值通常是十分容易的。在大多数编程语言中,有非常多的程序可用于生成均匀分布的随机数。然而有时我们可能需要处理更加任意的分布,如下图所示。
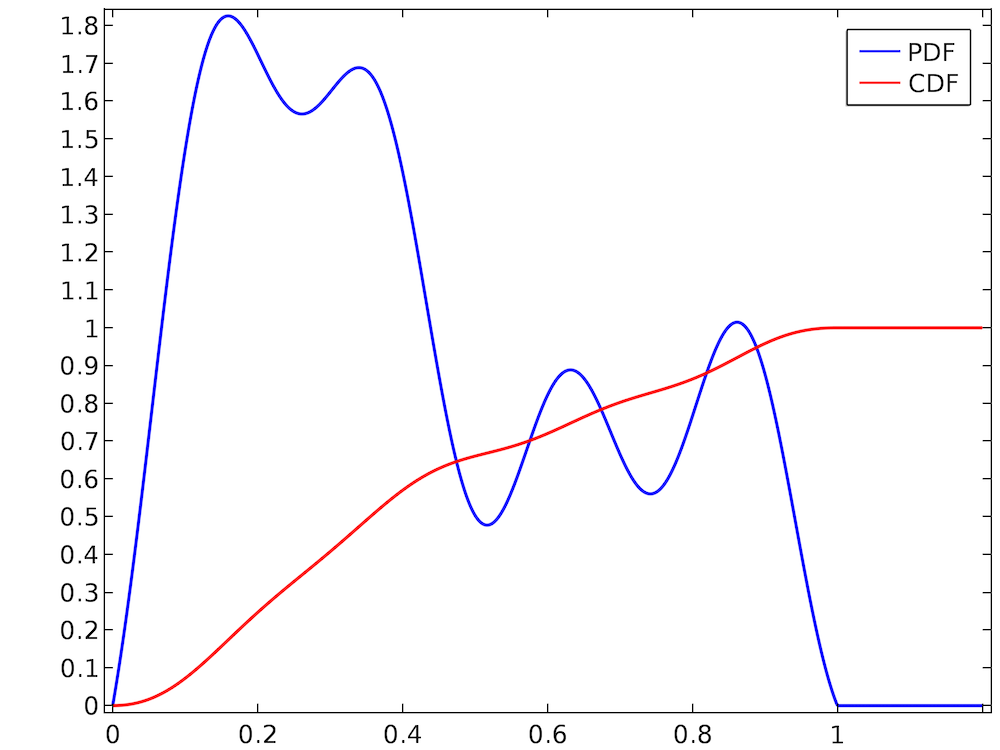
随机数在区间 (0, 1) 内取值,CDF 的最终值为 1,这表示 PDF 已被归一化。但是,随机数的分布显然并不均匀;例如相比于 (0.7, 0.8),随机数更有可能出现在范围 (0.2, 0.3) 内。在这种情况下,直接使用内置程序对间隔 (0, 1) 内均匀分布的随机数进行抽样,可能并不正确;我们必须想出另一种方法,从这个看似任意的 PDF 中抽取随机数。
为此,我们采用了一种从概率分布函数中取值的最基本方法——逆变换抽样。现在,将 U 定义为 0 到 1 之间均匀分布的随机数。换句话说,U 遵循方程(1)表示的分布函数。接着,为了从(可能不均匀的)概率分布函数 f(x) 中抽样随机数,我们需要执行了下列操作:
- 若函数 f(x) 尚未被归一化,则对其进行归一化。
- 求解归一化的 PDF f(x) 的积分,并由此计算出 CDF F(x) 的值。
- 对函数 F(x) 求逆,得出逆累积分布函数 或者分位数函数 F-1(x)。由于我们对 f(x) 进行了归一化,所以亦可称之为逆正态累积分布函数,或将其简单表述为逆正态 CDF。
- 将均匀分布的随机数 U 的值代入逆正态 CDF。
总而言之,当 U \in \left(0,1\right) 时,F-1(U) 是满足概率分布函数 f(x) 的随机数。接下来,我们将讨论一个具体案例,帮助您了解如何通过这种途径对不均匀的概率分布函数进行抽样。
示例 1:Rayleigh 分布
Rayleigh 分布 经常出现在稀薄气体动力学和束流物理的方程中,其表达式为
(2)
\begin{array}{cc}
0 & x \textless 0 \\
\frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right) & x\geq 0
\end{array}
\right.
其中 σ 是待指定的比例因子。如下所示,我们可以证实上方的 Rayleigh 分布函数已被归一化。
\int_{0}^{\infty} \frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right)dx
&= \lim_{x \rightarrow \infty} \left.-\exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)\right|^x_0\\
&= 1-\lim_{x \rightarrow \infty}\exp\left(-\frac{x^2}{2\sigma^2}\right)\\
&= 1
\end{aligned}
它的累积分布函数为
F(x)
&=\int_{0}^{x} \frac{x^\prime}{\sigma^2} \exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)dx^\prime\\
&= \left.-\exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)\right|^x_0\\
&= 1-\exp\left(-\frac{x^2}{2\sigma^2}\right)
\end{aligned}
下图绘制了当 σ = 1 时归一化的 Rayleigh 分布和它的累积分布函数。当 x 逐渐变大时,CDF 显然接近 1。
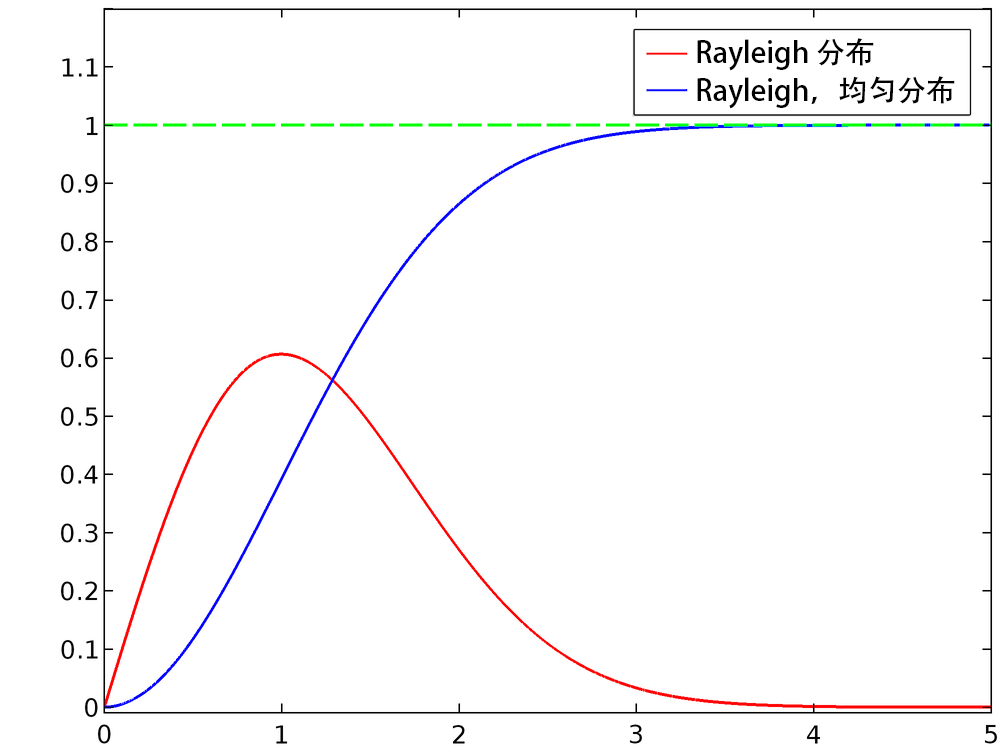
为了计算逆正态 CDF,我们设 y = F(x) 并求解 x 的值:
y &= F(x)\\
y &= 1-\exp\left(-\frac{x^2}{2\sigma^2}\right)\\
\exp\left(-\frac{x^2}{2\sigma^2}\right) &= 1-y\\
-\frac{x^2}{2\sigma^2} &= \log\left(1-y\right)\\
x &= \sigma \sqrt{-2 \log\left(1-y\right)}
\end{aligned}
现在将变量 y 替换为均匀分布的随机数 U,则
由于 U 在区间 (0, 1) 内呈均匀分布,并且其值当前未知,考虑上述情况,我们通过使 U 和 1 – U 精确遵循相同的概率分布函数,从而进一步简化上方的表达式。由此,我们得到了 x 的抽样值的最终表达式,
(3)
接下来,我们将讨论如何在 COMSOL 模型中通过使用方程(3)对 Rayleigh 分布的值进行抽样。
请注意,在计算逆正态 CDF 时,上述分析方法并非总是可行的。对于任何函数的积分,不一定始终存在闭合的解析解,而且累积分布函数的逆函数不一定存在对应的表达式。本文特意选择 Rayleigh 分布作为案例,正是因为我们可以推导出它的逆正态 CDF,而不需要数值或近似方法。
在 COMSOL Multiphysics® 中随机抽样
我们可以借助上述分析结果在 COMSOL Multiphysics 中对任意一维分布(例如 Rayleigh 分布)进行抽样。我们首先来介绍一下可用于从特定类型分布中抽样的内置工具。
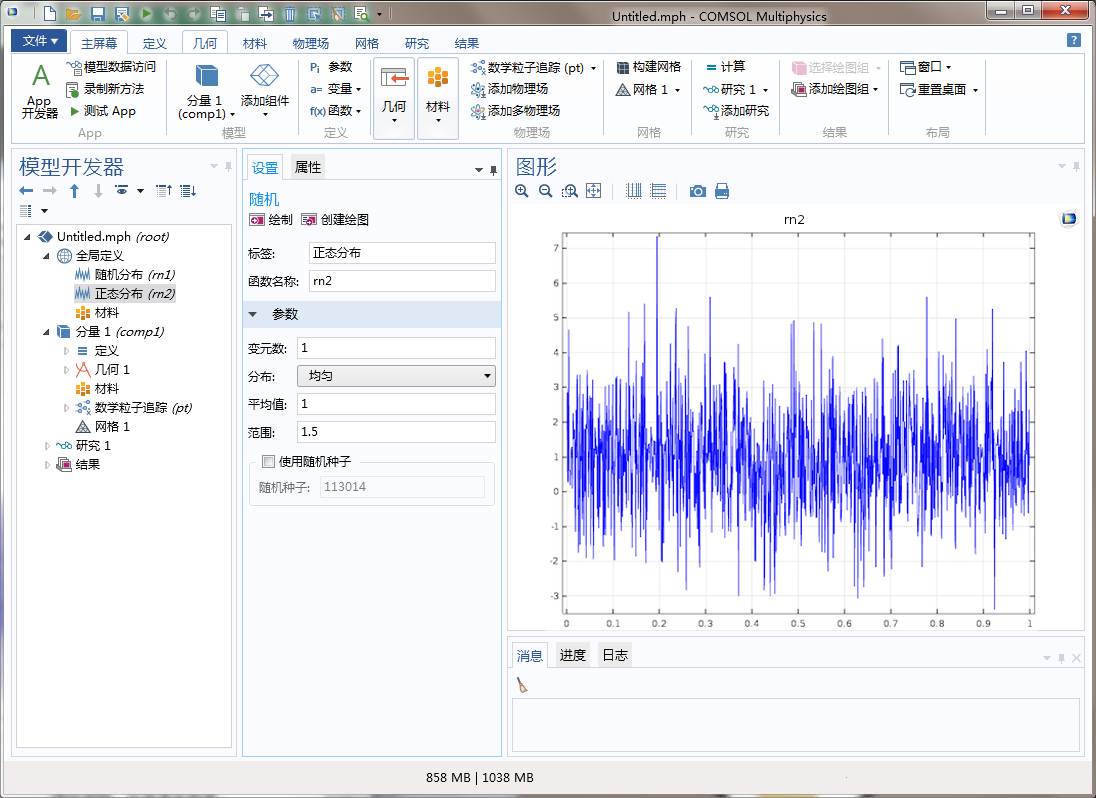
在 COMSOL Multiphysics 中,我们有多种定义伪随机数(稍后我们会解释“伪随机”的含义)的方法。例如,您可以使用全局定义 节点或定义 节点中的随机 函数特征,通过均匀分布或正态分布定义伪随机数。如果使用的是均匀 分布,请指定平均值 和范围。若平均值为 μu 且范围为 σu,则 PDF 为
\begin{array}{cc}
0 & x \leq \mu_u-\frac{\sigma_u}{2}\\
\frac{1}{\sigma_u} & \mu_u-\frac{\sigma_u}{2} \textless x \textless \mu_u + \frac{\sigma_u}{2}\\
0 & \mu_u + \frac{\sigma_u}{2} \leq x\\
\end{array}
\right.
当平均值为 1 且范围为 1.5 时,均匀分布的示例图如下。
当使用正态 分布或高斯分布时,请指定平均值 和标准偏差。若平均值为 μn 且标准偏差为 σn,则 PDF 为
当平均值设为 1,标准偏差为设 1.5,正态分布的示例图如下。与均匀分布的相同点在于,正态分布的曲线呈锯齿状,并且不可预测;不同之处是越靠近 y = 1,曲线上的点就越密集,而越向两边越稀疏。
在默认设置中,平均值为 0,范围或标准偏差为 1,此时两种分布的对比图如下。
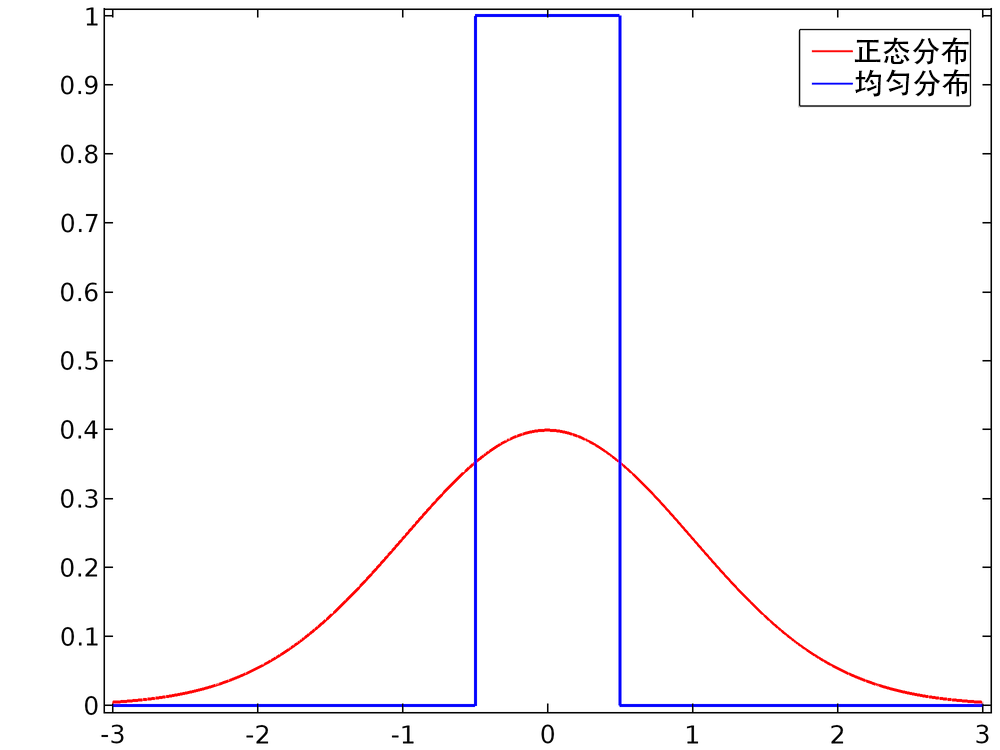
对比范围为 1 的均匀 PDF 和标准偏差为 1 的高斯 PDF。
除了“随机”函数特征,您也可以在任意表达式中使用内置函数 random 和randomnormal。random 函数呈均匀分布,平均值为 0,范围为 1; randomnormal 函数呈正态分布,平均值为 0,标准偏差为 1。
对于方程(3),我们需要在区间 (0, 1) 中均匀抽取一个数 U,有两种方法可以实现这一操作:
- 使用“随机”函数特征,并将平均值设为 0.5,范围设为 1。
- 使用内置的
random函数,并将平均值和范围增加 0.5。
尽管两种方法均是可行的,不过我们将在下文中采用第二种方法。
随机数,伪随机数与种伪随机种子
正如前文所述,采用上述方法的目的是生成伪随机数。伪随机数 指以初始值或种子 为起点,通过确定方式生成的随机数。对于内置的 random 函数来说,种子相当于函数的一个或多个变元。对比而言,真正的随机数不能仅仅凭靠一个程序而生成,它来源于自然的熵增——一种本质上不可预测、不可重复的自然过程,例如放射性衰减或大气噪声。
在许多方面,伪随机数使用起来会比真随机数更为方便。伪随机数的重复性特征可被用于排除 Monte Carlo 仿真的故障,这是因为使用同一个种子多次运行仿真可以得到相同的结果,这让识别模型的变化变得十分简单。由于不需要自然熵源,因而只能在有限的时间内从环境中收获有限的熵,所以伪随机数所需的仿真时间少于真随机数。
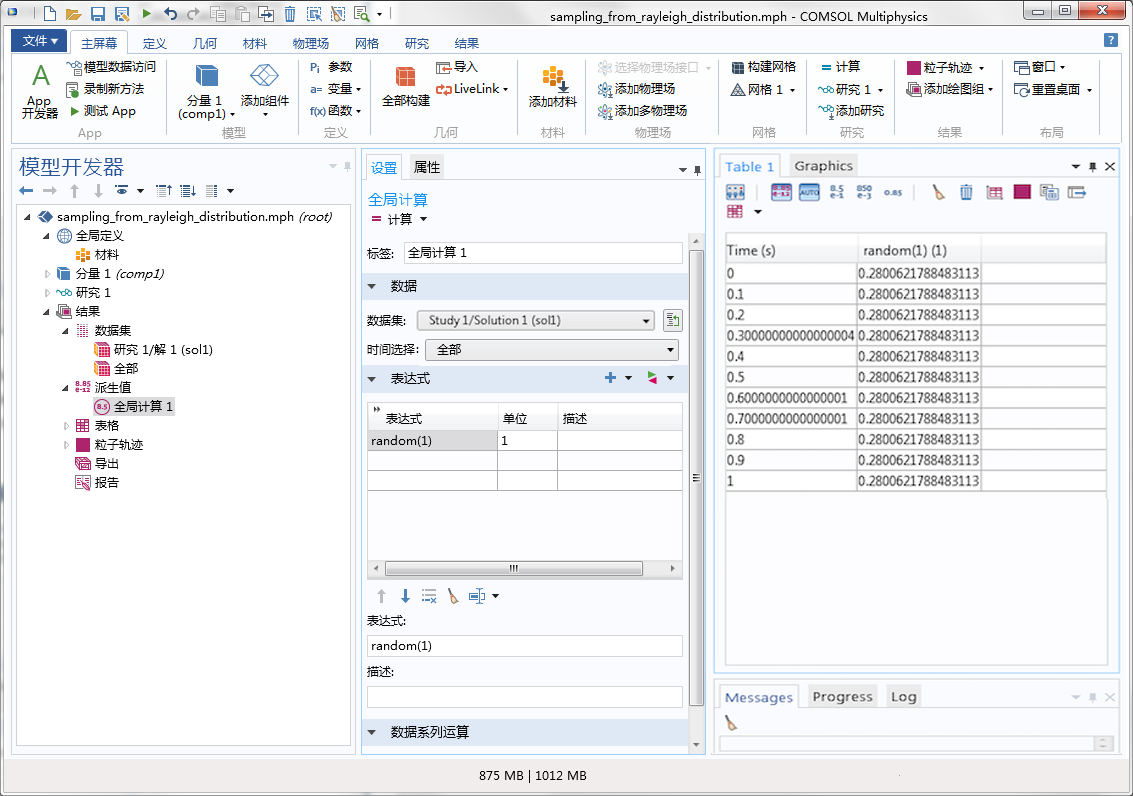
然而伪随机数也存在一些缺点,我们必须采取一些额外的预防措施。种子的数值不同,伪随机数也就不同,但是,相同的种子会反复生成相同的数字。若您想在任意的 COMSOL 模型中验证这一点,可以创建一个“全局计算”节点,并使用恒定种子反复对内置的 random 函数进行计算。现在假设该函数为 random(1),如下图所示,输出结果与“1”之间不存在明显的关联,因此从这个意义上来说似乎确实是“随机”的;然而若对表达式进行多次计算,得到的值则始终相同,并不会呈现随机分布。
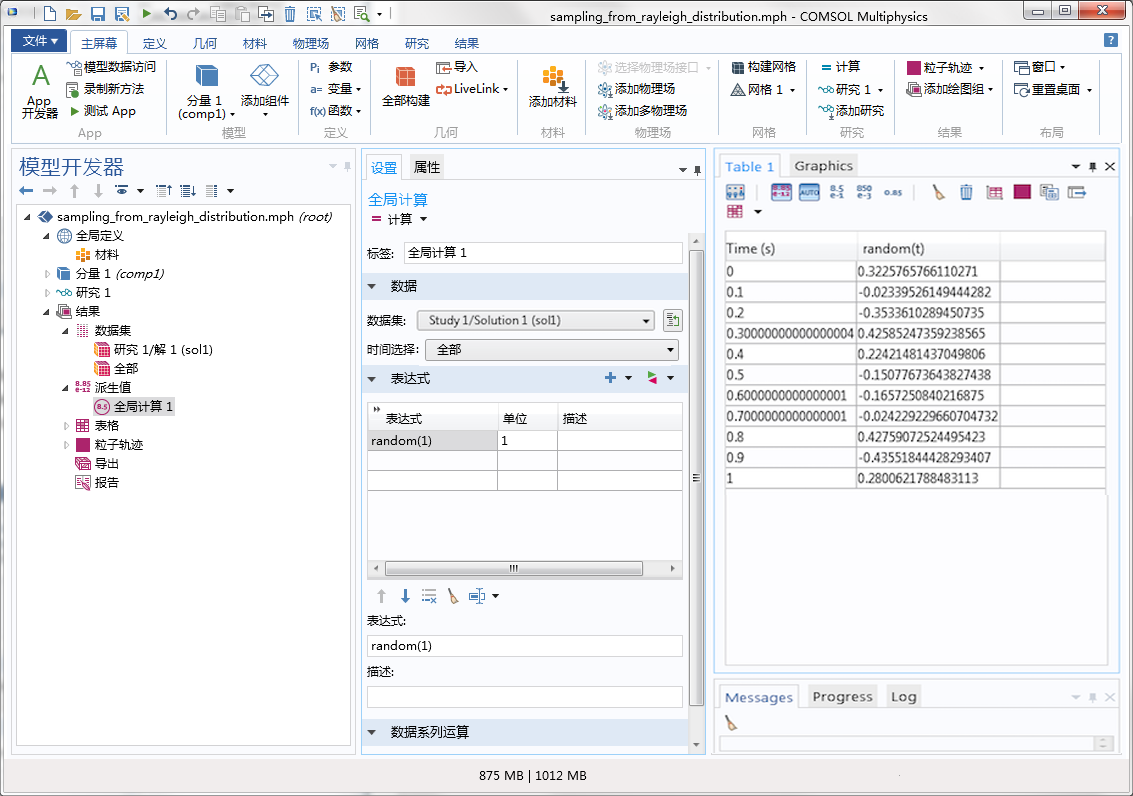
如果在每一次计算随机数时都使用不同的种子,那么每一次都会获得不同的结果。在下方的屏幕截图中,表格中的时间被用作随机函数的输入变元,我们可以将下图的计算结果与上图进行对比。
当模拟粒子系统时,Monte Carlo 仿真往往包含了大量的粒子集群,这些粒子在随机的初始条件下被释放,并受随机力的支配。此类涉及到粒子群随机现象的案例包括:
- 分布中抽样——本系列中后续的博客文章将对这些内容进行探讨
- 在稀薄背景气体中由随机电荷交换碰撞引起的离子中和
- 高雷诺数流体流动中粒子的湍流分散
- 模拟布朗运动引起的粒子扩散
显然,如果每个粒子得到了完全相同的伪随机数,那么仿真将完全与物理现场相悖。举例来说,就是当离子与背景气体相互作用时,所有离子会在同一时刻与气体分子或原子发生碰撞。为了让粒子是独一无二的,粒子仿真中涉及到的随机数必须具有唯一的种子。
一种方法是将粒子索引 用作种子的一部分,得到的整数与每一个粒子唯一对应。粒子索引变量为 <scope>.pidx,其中 <scope> 是物理场接口实例的唯一标识符。在数学粒子追踪 接口中,粒子索引通常为 pt.pidx 。函数 random(pt.pidx) 将为每个粒子分配不同的伪随机数。
若粒子在整个过程中都由随机的力支配,这将产生一个新的问题。举例来说,当使用随机数确定离子是否与气体分子发生碰撞时,您可不希望每一次都为特定粒子分配同一个随机数——否则的话,粒子只能在一个时间步长上发生碰撞或者干脆不碰撞!解决方案是:在随机数种子中引入多个变元,使其至少包含一个与其他粒子不同的变元和一个随仿真时间变化的变元。如果仿真需要对多个伪随机数进行互不干涉的抽样,那么或许需要再添加新变元。随机函数在使用时通常采取 random(pt.pidx,t,1) 的形式,当然,如果确实需要额外的独立伪随机数,我们可以将最终变元 1 替换成其他数字。
Rayleigh 分布的结果
我们来回顾一下最初的 Rayleigh 分布抽样问题。假设我们有一个粒子群,并希望对每个粒子抽样一个数,使结果值符合 Rayleigh 分布。此案例中我们会使用到 σ = 3 的方程(2)。在 COMSOL 模型中定义以下变量:
| 名称 | 表达式 | 描述 |
|---|---|---|
rn
|
0.5+random(pt.pidx)
|
Random argument
|
sigma
|
3
|
Scale parameter
|
val
|
sigma*sqrt(-2*log(rn))
|
Value sampled from Rayleigh distribution
|
请注意,最后一行便是方程(3)。下方的直方图为由 1000 个粒子组成的集群的 rn 值。平滑曲线代表精确 Rayleigh 分布,在这里,我们通过解析 函数特征对其进行定义。
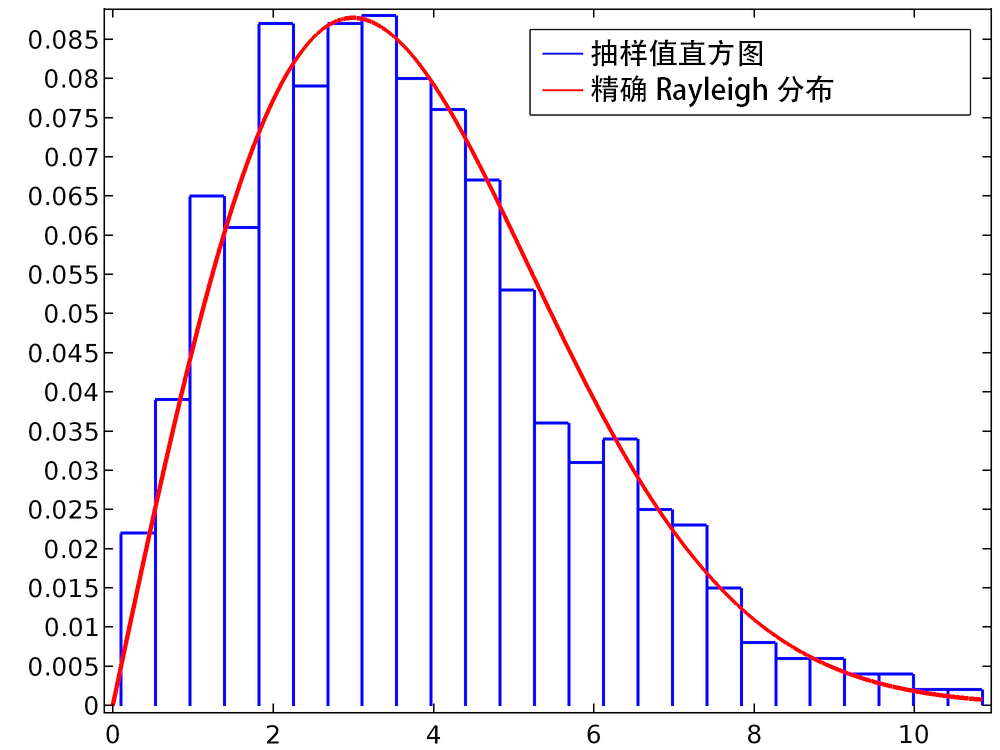
如果您想绘制出包含更丰富信息的精细曲线,那么需要添加更多的粒子来精确地捕获概率分布函数。
插值函数的注意事项
如果将概率分布函数作为插值 函数特征,而不是解析 或分段 函数输入到 COMSOL Multiphysics 中,那么便可通过内置功能自动对随机函数进行定义,此随机函数会从指定的 PDF 中进行抽样。
假设我们的插值函数会对下表中的数据点进行线性插值:
| x | f(x) |
|---|---|
| 0 | 0 |
| 0.2 | 0.6 |
| 0.4 | 0.7 |
| 0.6 | 1.2 |
| 0.8 | 1.2 |
| 1 | 0 |
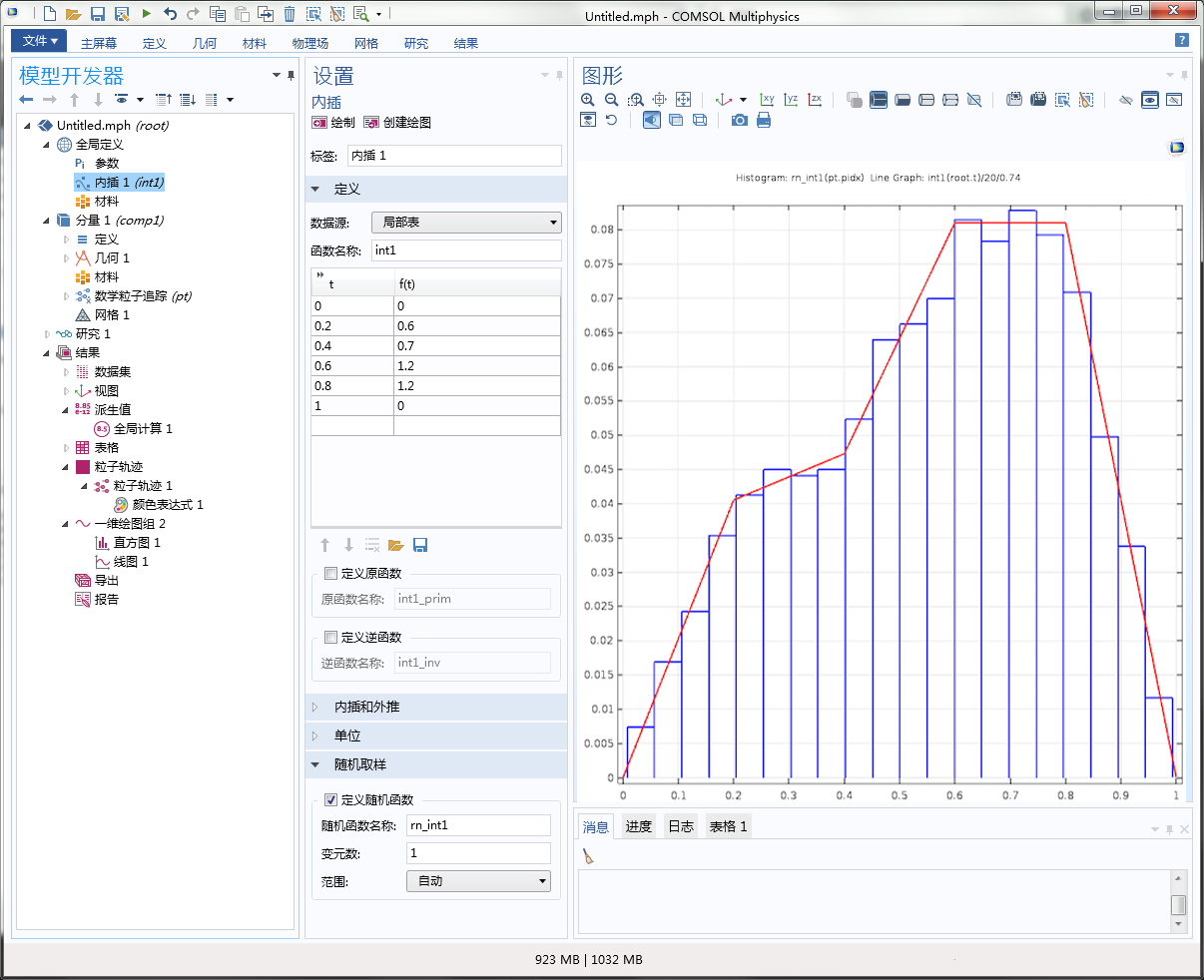
下方的软件截图演示了如何将这些数据输入到“插值”函数中。具体操作方式是打开“插值”函数特征的设置窗口,并勾选定义随机函数 复选框,便能自动对函数 rn_int1 进行定义,此函数可对该分布进行抽样。在“图形”窗口中,直方图显示了 1000 个数据点的随机抽样结果,连续曲线便是插值函数本身。我们还添加了 20 和 0.74 这两个额外的因子,分别用于修正直方图柱条的数目和对插值函数进行归一化处理。
概率分布函数的优势
在本文中,我们解释了概率分布函数、累积分布函数以及与各自逆函数之间的关系。同时还探讨了几种适用于对 COMSOL 模型中的均匀和非均匀概率分布函数进行抽样的技术。在束流物理场中的相空间分布系列的下一篇文章中,我们将对离子束和电子束的物理现象进行阐述,并会阐述为何概率分布函数对于准确模拟束流系统来说是至关重要的。
参考文献
- Humphries, Stanley. Charged particle beams. Courier Corporation, 2013.
- Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.



评论 (2)
Lydia Wong
2018-09-26Hello, may I want ask for help with random function? I am drawing some circles, maybe 50, in a rectangle with specific length and width. I want to put the circles in random locations in the rectangle. So I plan to put 50 random points first. I can use the random funtion in Global Parameter but it only gets one location. Do you know how to do this?
王 刚
2018-10-19 COMSOL 员工Hi, perhaps you need to read another blog, http://www.comsol.com/blogs/how-to-create-a-randomized-geometry-using-model-methods/