RF 模块中的 端口 边界条件是 COMSOL Multiphysics® 软件的附加功能,可用于发射和吸收电磁能。在本篇博客中,我们将介绍如何设置一个圆形波导端口,并检查定义端口模场的解析解。另外,我们还从端口方向分析了一个用于功率传输的圆形端口偏振,并将模型扩展到高阶模式。
用于描述简并模式的圆形端口参考轴
为了模拟波在圆形波导中的传播,我们需要通过描述模场的边界条件来设置激励和终止。但是,圆形端口显示出简并性,使得其在模场方向上产生不确定性。下面我们将一起讨论如何使用 圆形端口参考轴 子功能来抑制圆形波导端口中的角简并。
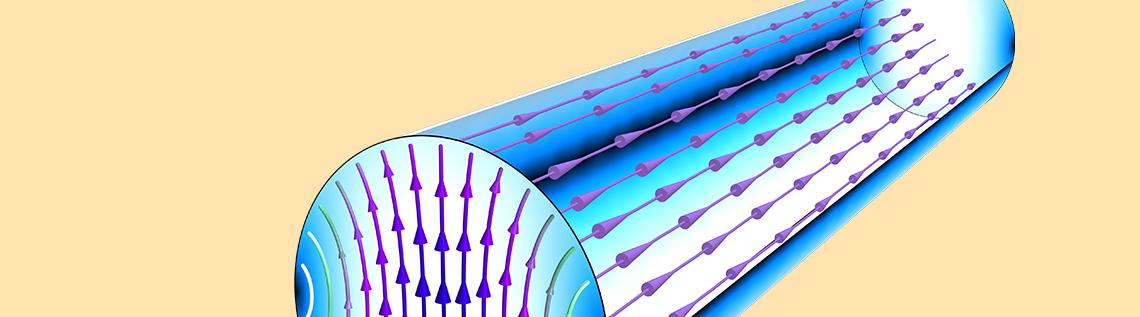
主导模 TE11 表现出简并性。使用“圆形端口参考轴”子功能固定模场的方向。
首先,进行 模式分析 研究,以在一个二维的简单圆上找到共振模,代表端口边界。在默认返回的模式中,有些是围绕原点进行完全相同的 TE11 模式形状的简单旋转。那么,我们如何确定哪种解是正确的呢?所有这些描述圆形波导(参考文献 1)横向场分量的方程都有同等精度的解:
E_{\rho}=\frac{-j\omega\mu m}{k_{c}^{2}\rho}(A \ cos \ m\phi-B \ sin \ m\phi) \ J_{m}(k_{c}\rho) \ e^{-j\beta z}E_{\phi}=\frac{j\omega\mu}{k_{c}}(A \ sin \ m\phi+B \ cos \ m\phi) \ J’_{m}(k_{c}\rho) \ e^{-j\beta z}
H_{\rho}=\frac{-j\beta}{k_{c}}(A \ sin \ m\phi+B \ cos \ m\phi) \ J’_{m}(k_{c}\rho) \ e^{-j\beta z}H_{\phi}=\frac{-j\beta m}{k_{c}^{2}\rho}(A \ cos \ m\phi-B \ sin \ m\phi) \ J_{m}(k_{c}\rho) \ e^{-j\beta z}
式中,m 表示第一模式索引的值,Jm 是第一类贝塞尔函数,J’m 是贝塞尔函数的导数。自变量为截断波数 kc=χ’mn/a。

端口圆周上的两个点用于定义边界场的方向。我们可以想象成用一条线连接每个选择中的两个点以形成参考轴。
因为圆形端口是简并,所以出现了看似相同的模式。这意味着给定模场的无限次旋转可以存在于同一边界上,这对于描述端口模场相对于其他模场的方向可能是有问题的。因此,我们定义了一个圆形端口参考轴,它可以作为端口节点的子功能使用。此功能使我们可以在端口圆周上选择两个顶点,用于定义端口边界上场的方向。根据该参考轴定义模场,其方向上的任何不确定性都得以解决。现在我们可以将圆形端口的研究扩展到三维。
TE11 模通过圆形波导传播。等值线图的动画显示了 E 场的 z 分量,该分量是使用完整的动态数据扩展序列类型创建的。箭头图描述了端口边界上的电模场。
模拟圆形波导偏振
下面,我们以 RF 案例库中的圆形端口偏振模型教程为例,介绍如何模拟一个圆形波导偏振。本教程演示了如何使用简并端口模式来激励和终止端口。所研究的结构是一个被理想导电壁包围的笔直的圆形波导。
与任何 COMSOL Multiphysics 模型一样,我们从构建几何、分配材料,然后设置物理场开始。本案例中的结构是一个充满空气的简单圆柱体。我们使用理想电导体边界条件模拟外部的金属边界。由于此条件假定导体是无损耗的,因此不需要为这些边界分配材料。接下来,我们添加端口边界条件,并在波导的一端选择圆形边界。
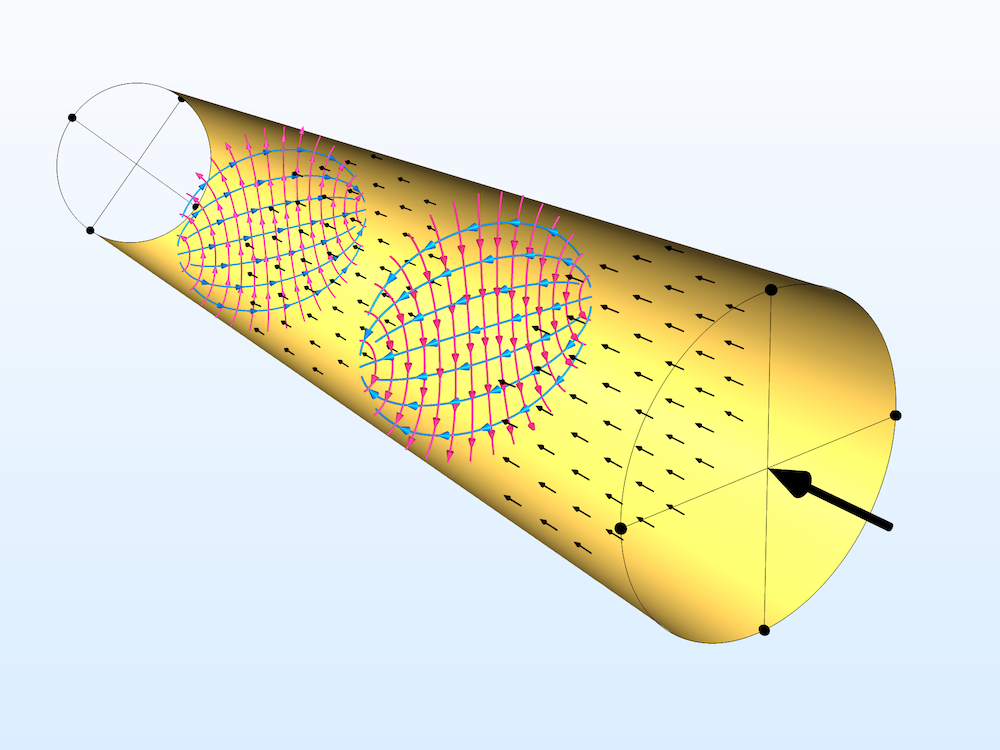
波导的外壁被模拟为“理想电导体” 边界。红色线条表示电场的流线,蓝色线条表示磁场。箭头图(黑色)表示从激励端口到侦听器端口的功率流。实线表示近端端口1 和 2 以及远端端口 3 和 4 的参考轴。
在“端口1”设置中,我们首先将几何类型设置为圆形。使用圆形端口时,必须明确模式类型(TE 或 TM)和模式编号。TE 和 TM 分别代表横电和横磁。圆形端口支持这两种模式类型。圆形模式编号由上述的横磁场和横电场方程中使用过的两个指数 m 和 n 来描述。
我们对主导 TE11 模式感兴趣。因此,在端口1 设置中,将模式类型设置为 TE 并将模式编号设置为 11;在圆形端口参考轴子功能的端口圆周上选择两个相反的顶点。现在,重点是我们如何在波导的另一端终止该模式?
任何入射场都可以被具有相同模场形状的两个相互正交的端口完全终止。我们可以通过扩展圆形波导偏振模型来验证这一点,并以此研究侦听器端口的参考轴相对于激励端口的参考轴旋转时的透射率。在此模型中,我们总共设置了四个端口,其中只有一个是激励端口(端口1)。相互正交的端口1 和 2 一起接收所有反射的能量,而相互正交的端口3和4接收所有透射的能量。
最后,进行参数化扫描,其中端口3和4的参考轴一起绕原点旋转角度Ɵ。下图在x轴上绘制了该旋转角度。S参数可以作为内置表达式使用,在后处理中进行评估。可以将传输到端口3和4的功率比分别评估为S 31和S 41的平方。我们使用此关系评估横跨下图的每个角度的透射率。
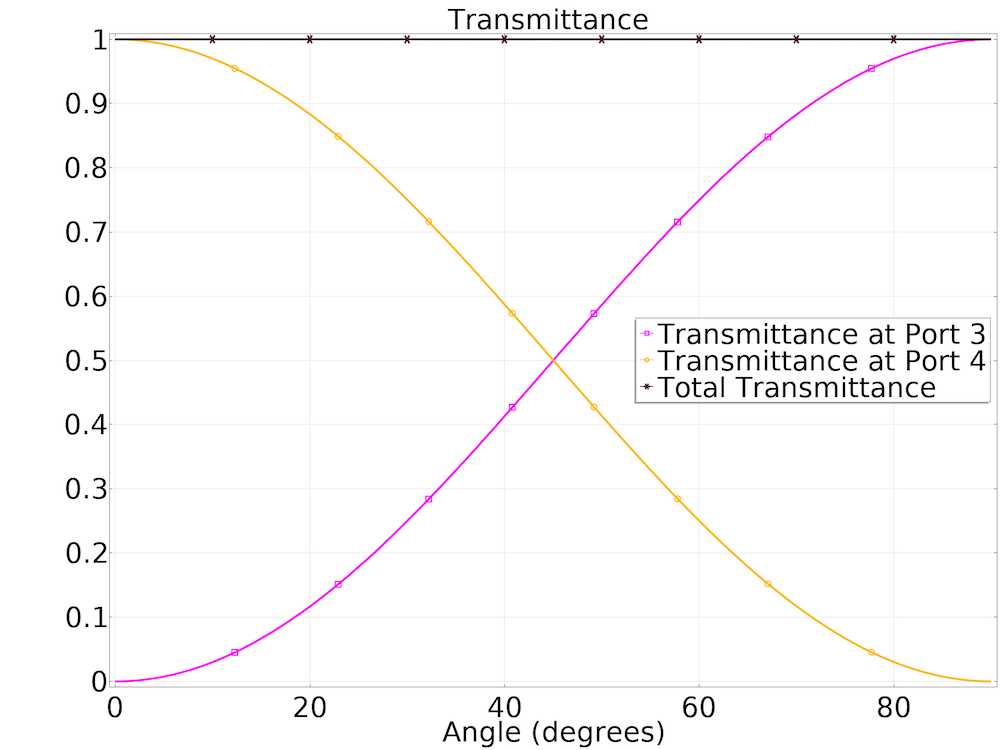
在任何角度下,透射率值之和为 1,表示反射几乎为零,因此是理想的终止条件。如果第二接收端口的参考轴是第一接收端口围绕波导轴旋转 90°得到的,则可以自由选择第一接收端口的参考轴。
一个重要因素:截止频率
当我们期望激励波导或端口时,都必需要考虑结构的截止频率,即特定模式可以传播的最低频率。不仅对于主导模式,而且对于高阶模式都是如此。矩形、圆形和同轴端口都具有截止频率的解析表达式。该值取决于结构的大小、内部的介质以及模式编号。下面是圆形波导中TE模式和TM模式的截止频率方程:
f_c=\frac{\chi'{mn}}{2\pi a \sqrt{\mu\epsilon}},用于 TE 模式
f_c=\frac{\chi{mn}}{2\pi a \sqrt{\mu\epsilon}},用于 TM 模式
式中,a 是半径,μ 是磁导率,ε 是介电常数。
χ’mn 的值通过贝塞尔函数 Jm(x) 的导数的零点给出,该值是确定 TE 模式的截止所必需的。χmn 的值由贝塞尔函数的零点给出,该值为确定TM模式的截止所必需的。一般情况下,贝塞尔函数的零点及其一阶导数都是已知的,下面列出了其中的一些值。
我们发现,χ’mn 表格当中的 m = 0 列中的值和 χmn 表格当中m = 1列中的值是相同的。因此,TE0n 和 TM1n 模式具有相同的截止频率,并被称为简并模式。
| 模式索引 | m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 |
|---|---|---|---|---|---|---|
| n = 1 | 2.4049 | 3.8318 | 5.1357 | 6.3802 | 7.5884 | 8.7715 |
| n = 2 | 5.5201 | 7.0156 | 8.4173 | 9.7610 | 11.0647 | 12.3386 |
| n = 3 | 8.6537 | 10.1735 | 11.6199 | 13.0152 | 14.3726 | 15.7002 |
在 TM 模式中使用的第一类贝塞尔函数 Jm(x) 的零点χmn。(参考文献2)
| 模式索引 | m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 |
|---|---|---|---|---|---|---|
| n = 1 | 3.8318 | 1.8412 | 3.0542 | 4.2012 | 5.3175 | 6.4155 |
| n = 2 | 7.0156 | 5.3315 | 6.7062 | 8.0153 | 9.2824 | 10.5199 |
| n = 3 | 10.1735 | 8.5363 | 9.9695 | 11.3459 | 12.6819 | 13.9872 |
用于 TE 模式的第一类贝塞尔函数 J’m(x) 导数的零点 χ’mn 。(参考文献 2)
给定波导中的模式数量随频率增加。下图中,我们以截止频率递增的顺序展示了圆形端口的前 24 个模式。
 TE11 TE11 |
 TM01 TM01 |
 TE21 TE21 |
 TM11 TM11 |
 TE01 TE01 |
 TE31 TE31 |
 TM21 TM21 |
 TE41 TE41 |
 TE12 TE12 |
 TM02 TM02 |
 TM31 TM31 |
 TE51 TE51 |
 TE22 TE22 |
 TE02 TE02 |
 TM12 TM12 |
 TE61 TE61 |
 TM41 TM41 |
 TE32 TE32 |
 TM22 TM22 |
 TE13 TE13 |
 TE71 TE71 |
 TM03 TM03 |
 TM51 TM51 |
 TE42 TE42 |
圆形端口的前 24 个模式。 TE 模式展示了电场模的表面图和磁场的箭头图。 TM 模式展示了磁场模的表面图和电场的箭头图。
使用“方法”工具自动收集数据
为了得到上图,我们使用了一种被称为加速建模工作流程 方法的强大工具。该方法包含一系列命令。调用方法时,这些任务将在软件内自动运行。这里,我们使用一种方法来自动化和加速生成圆形端口前24个模式的场分布的过程。该方法按顺序执行以下操作:
- 计算给定模式的截止频率
- 在端口 节点设置中输入模式编号
- 以略高于截止的频率值运行模型,并将解存储在端口边界
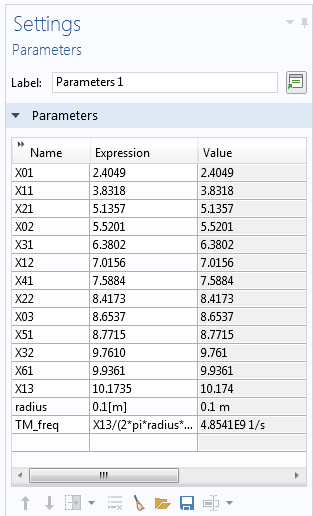
针对每种模式循环,该方法使用各自的 χmn / χ’mn 常数(其值在 参数节点中输入)执行此过程。
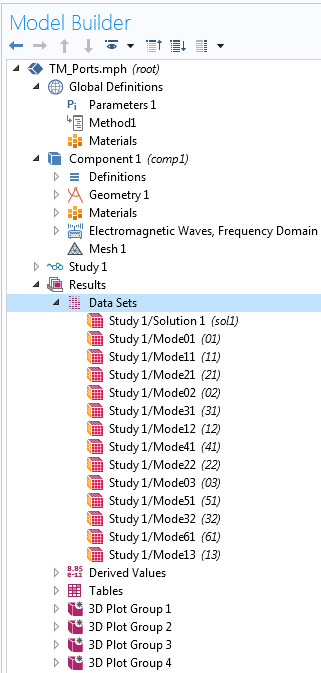
每个模式编号的贝塞尔函数的零点都作为参数输入(左)。这些参数在方法 1(如下图所示)中使用,用于计算每个模式编号(右)的解集,且正好在截止频率之上。
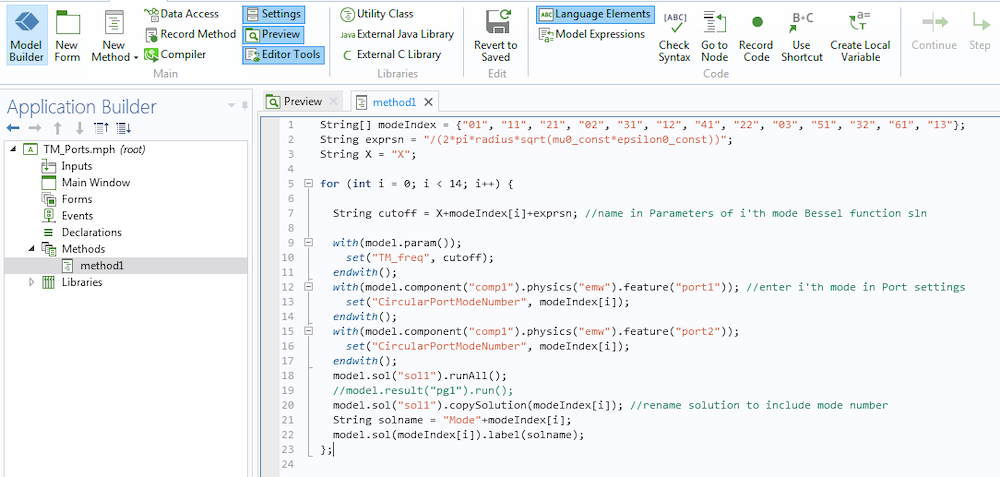
一种用于简化 TM 模式求解过程的方法。我们可以使用类似的方法自动生成每种模式的图。
结语
本篇博客概述了如何使用圆形端口进行波导激励和终止。虽然这里仅针对圆形端口进行讨论,但请记住,在使用其他端口类型时也必须考虑截止频率。矩形和同轴端口的唯一不同是它们有各自的截止频率方程,这些方程也是模式编号和端口尺寸的函数。通过使用类似的方法,我们可以有效地实现这些端口类型的模式形状的可视化。
如果您对圆形端口建模有疑问,请联系COMSOL 技术支持。
后续操作
单击下面的按钮进入 COMSOL 案例库,尝试对本博客文章中介绍的圆形波导偏振进行仿真建模。您可以使用 COMSOL Access 帐户登录,并使用有效的软件许可证下载 MPH 文件。
参考文献
- David M. Pozar, Microwave Engineering, John Wiley & Sons, 1998.
- Constantine A. Balanis, Advanced Engineering Electromagnetics, John Wiley & Sons, 1999.



评论 (0)