Menu
COMSOL 博客

模拟物体在基板上的光散射

Author Image
作者 Walter Frei
2020年 4月 14日

在电磁波仿真中，我们经常遇到的一种情况是：均匀介电基板上表面刻蚀结构的光散射。在这篇博客中，我们将介绍一种在 COMSOL Multiphysics® 软件中模拟这种情况的方法。

背景和概述

考虑一个小型光散射体：介电基板表面的金制半圆柱体。我们研究仅存在单个散射体的情况。假设一束准直光线，其直径远大于散射体，所及几乎可以近似为一个平面波。平面波以任意的角度和偏振态入射到半圆柱体结构。假设介电基板在负 Z 轴方向无限延伸。

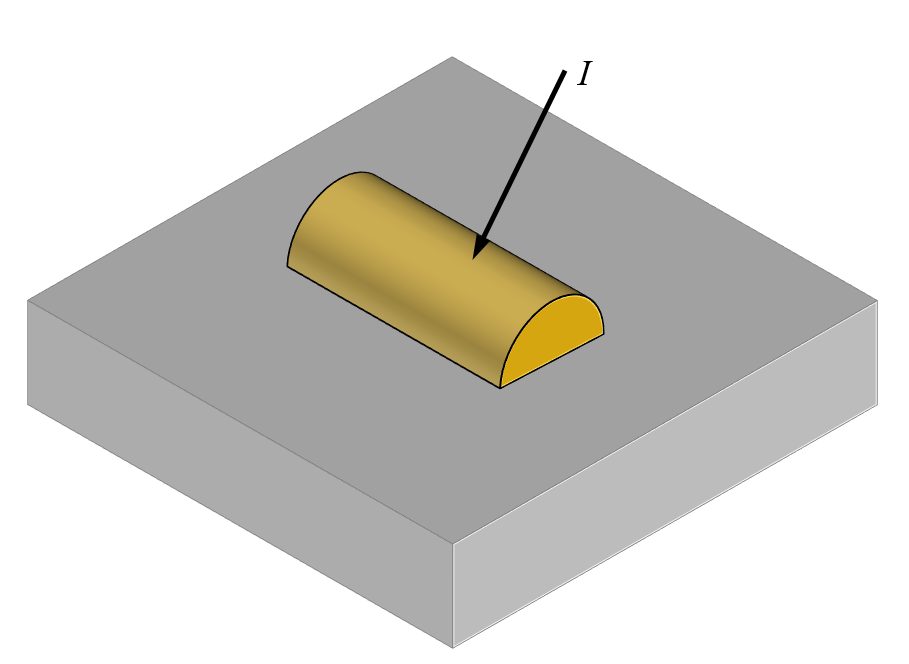
光入射到介电基板上的单个散射体上的示意图
光以任意角度入射到半无限介电基板表面的单个散射体上。

由模拟的是单个散射体，可以将其表征为对背景场的一个微扰，因此使用散射场公式是合理的。这个公式需要输入一个背景电场，代表没有散射体时麦克斯韦方程的解。也就是说，以频域的形式求解麦克斯韦方程组：

\nabla \times \left( \mu_r \nabla \times \mathbf{E}_{total} \right) – \frac{\omega^2}{c_0^2}\left( \epsilon_r – \frac{i \sigma}{\omega\epsilon_0}\right) \mathbf{E}_{total}= 0

但是，将总电场写成以下形式：

\mathbf{E}_{total} = \mathbf{E}_{relative} + \mathbf{E}_{background}

我们求解的不是总场，而是相对场（常称为散射场）。背景电场是在没有散射体的情况下，有关域上麦克斯韦方程组的解。对于自由空间中的物体，背景场只是一个平面波，比如 RF 模块的基准示例：计算理想导体球的雷达散射截面对比了使用这种方法计算的数值解与解析解。波动光学模块中也有一个类似的示例，它计算了金纳米球的光散射。可能有人会尝试用同样的方法，求解半无限空间上的介电质，但这会导致背景场出错。

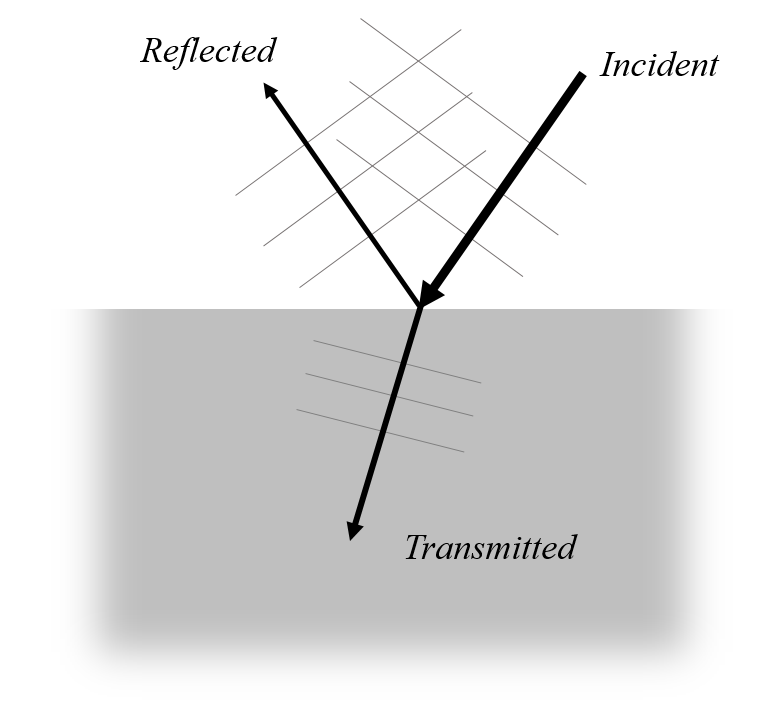
没有散射体的介电界面电场示意图
不存在任何散射体的情况下，电介质界面的电场为入射、反射和透射的平面波之和。

对于半无限无损介电基板上的散射体，背景场方程必须包括界面上的反射和折射。一种方法是基于单独的分析计算场，并将该场用作背景场。COMSOL 案例库中的基板上的颗粒散射教程模型对这种方法进行了演示。但在本文示例中，我们直接将解析解作为入射到无限介电基板的背景场输入。

使用菲涅耳方程定义背景场

菲涅耳方程与斯涅耳定律共同描述了平面光波入射到具有不同折射率的两种材料之间界面时的反射和传输。这方程首先定义了入射平面，即由垂直于两种材料交界面的法向量和入射平面波的波向量描述的平面。入射电场被分解为一个完全垂直于该平面的分量，称为 s 极化或 TE 波，以及一个完全平行于该平面的分量，称为 p 极化或 TM 波。例如，圆偏振光是相同量级的 TE 波和 TM 波的总和，但彼此相位相差 90°。

在入射平面内，可以使用斯涅耳定律，将入射光(\theta_i)和透射光(\theta_t)相对于表面法线的角度与两种材料的折射率 n_a 和 n_b 相关联:

\frac{\sin \theta_t}
{\sin \theta_i}= \frac{n_a}{n_b}

菲涅耳方程为用于计算 TE- 和 TM- 极化的反射和透射系数：

\begin{array}
rr_{TE} = \frac{n_a \cos \theta_i – n_b \cos \theta_t}{n_a \cos \theta_i + n_b \cos \theta_t} \\
t_{TE} = \frac{2 n_a \cos \theta_i}{n_a \cos \theta_i + n_b \cos \theta_t} \\
r_{TM} = \frac{n_b \cos \theta_i – n_a \cos \theta_t}{n_b \cos \theta_i + n_a \cos \theta_t} \\
t_{TM} = \frac{ 2 n_a \cos \theta_i }{n_b \cos \theta_i + n_a \cos \theta_t}
\end{array}

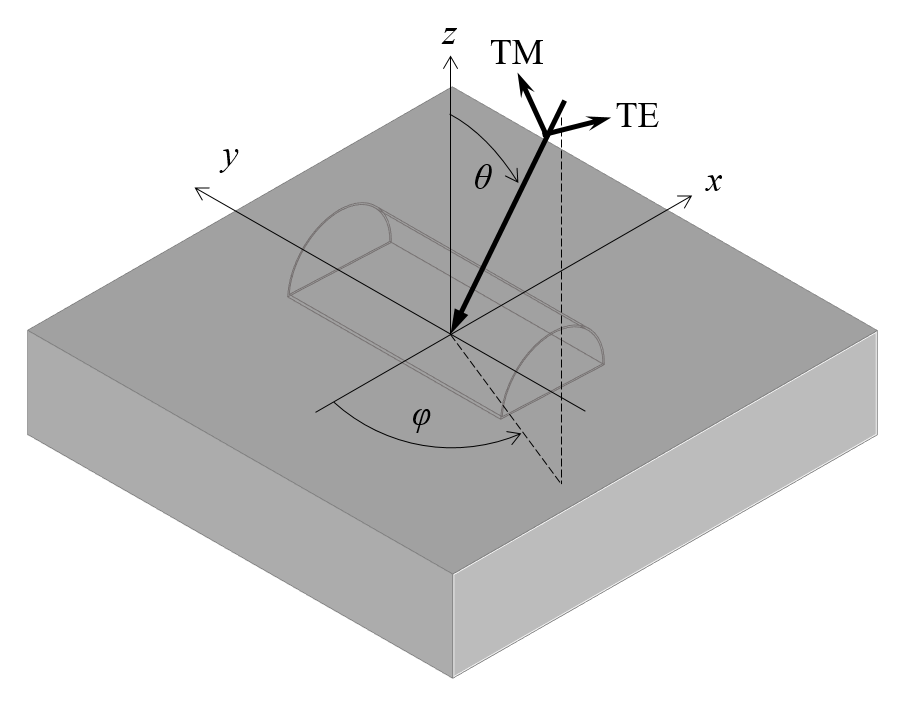
显示入射平面波的 TE 和 TM 极化分量的示意图
必须将入射平面波的 TE 和 TM 极化分量从入射平面转换回全局直角坐标。

接下来，必须将这些极化分量从入射平面转换回全局直角坐标，以得到入射和透射光束的 k 向量。按照惯例，交界平面是 xy 平面，入射光束在负 z 方向传播，将入射角 \theta 定义为与 z 轴的夹角，角度 \phi 定义为从负 x 轴开始绕 z 轴旋转的角度，如上图所示。因此，入射光束的 k 向量可定义为：

\mathbf{k}_i = \frac{2 \pi n_a}{\lambda_0} \left

透射光束的 k 向量可定义为：

\mathbf{k}_t = \frac{2 \pi n_b}{\lambda_0}\left

反射光束的 k 向量 \mathbf{k}_r 与入射光束相似，但 z 向分量的符号相反。

已知由 TE 和 TM 极化分量组成的入射光束，E_{i,TE} 和 E_{i,TM}，入射光束的电场分量为：

E_{i,x} = (E_{i,TM} \cos \theta_i \cos \phi – E_{i,TE} \sin \phi )\exp (-i\mathbf{k}_i \cdot \mathbf{x})
E_{i,y} = (E_{i,TM} \cos \theta \sin \phi + E_{i,TE} \cos \phi )\exp (-i\mathbf{k}_i \cdot \mathbf{x})
E_{i,z} = E_{i,TM} \sin \theta_i \exp (-i\mathbf{k}_i \cdot \mathbf{x})

对于反射分量：

E_{r,x} = (-r_{TM} E_{i,TM} \cos \theta_i \cos \phi – r_{TE} E_{i,TE} \sin \phi )\exp (-i\mathbf{k}_r \cdot \mathbf{x})
E_{r,y} = (-r_{TM} E_{i,TM} \cos \theta_i \sin \phi + r_{TE} E_{i,TE} \cos\phi )\exp (-i\mathbf{k}_r \cdot \mathbf{x})
E_{r,z} = r_{TM} E_{i,TM} \sin \theta_i \exp (-i\mathbf{k}_r \cdot \mathbf{x})

因此，入射侧的总背景场为 \mathbf{E}_{background} = \mathbf{E}_i + \mathbf{E}_r，另一侧的背景场为 \mathbf{E}_{background} = \mathbf{E}_t，其分量为：

E_{t,x} = (t_{TM} E_{i,TM} \cos \theta_t \cos \phi – t_{TE} E_{i,TE} \sin \phi )\exp (-i\mathbf{k}_t \cdot \mathbf{x})
E_{t,y} = (t_{TM} E_{i,TM} \cos \theta_t \sin \phi + t_{TE} E_{i,TE} \cos \phi )\exp (-i\mathbf{k}_t \cdot \mathbf{x})
E_{t,z} = t_{TM} E_{i,TM} \sin \theta_t \exp (-i\mathbf{k}_t \cdot \mathbf{x})

COMSOL Multiphysics® 软件中，这些表达式可以在不同域作为一组变量输入，并作为背景场定义。

光散射模型示例及讨论

点击文末链接，进入COMSOL案例库下载应用上述方法建立的模型。该模型计算并绘制了一个金制半圆柱散射体中的电场大小和损耗。

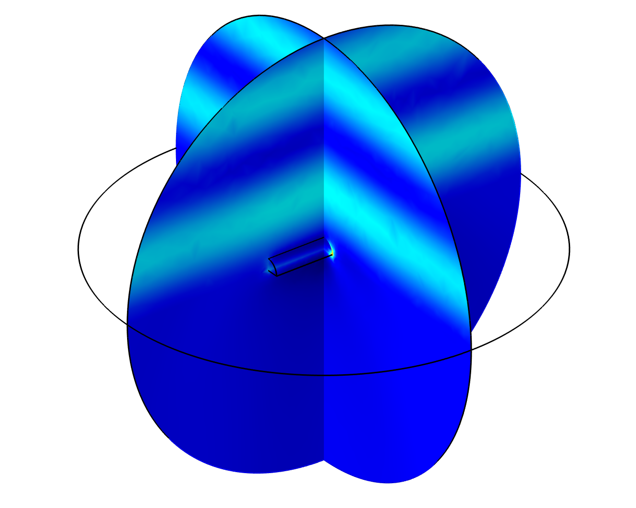
在 COMSOL Multiphysics 中建模的金散射体周围的电场强度
介电基板上的金制散射体周围的电场大小。

模拟显示金散射体中的光散射
金制散射体的损耗

虽然这种输入分析背景场的方法需要在模型设置方面多做一点工作，但它比 基板上的颗粒散射示例模型运行得更快，后者需要先要计算背景场。后一种模型方法适用于解析解求解比较困难，甚至不可能求解的情况。因此，对于均匀介电基板，前一种方法可能较好。

下一步

点击下方按钮，尝试使用解析的背景场分析基板上的散射体。

获取 MPH 文件

博客分类

相关主题

评论 (0)

正在加载...
浏览 COMSOL 博客
类别
标记
Baidu
map