在设计的早期阶段,例如,在设计特斯拉微阀的时候,我们可以使用拓扑优化获得装置几何结构设计的灵感。从 5.4 版本开始,COMSOL® 软件新增的密度模型功能使这种优化问题的设置变简单。在这篇博客中,我们展示了如何使用 COMSOL® 5.5 版本的形状优化功能来优化一个简单的设计,而这种设计的灵感来源则是比较复杂的拓扑优化结果。
特斯拉阀的机理
特斯拉阀是一种具有大各向异性流动阻力的装置,也就是说,在某一个方向上推动流体比其他方向明显更容易。因此,由于不含活动部件,这类装置可以作为稳固的泄漏阀使用。
我们可以考虑让两个流动方向的压降相同,并对流速比进行优化,但根据具体情况,固定流速比和优化压降比可能更有意义。如特斯拉微阀优化教程模型所述。
因此,数字双极性 Di被最大化,其定义为
其中,\Delta p_{\leftarrow} 和 \Delta p_{\rightarrow} 是两个流动方向的压降。
特斯拉阀是利用惯性效应的非线性本质开发的,所以如果流速很小,惯性效应将消失,物理场就变为线性。在这样的流态下,阀将不工作,即双极性为1。非线性的强度可以用雷诺数 Re 来量化表示,定义如下
其中,\rho 是密度,\mu 是黏度,U_\mathrm{in} 是特征速度,D 是特征长度尺度。
雷诺数超过 1000 往往会产生瞬态流动,而低于 10 的雷诺数,惯性效应太小。因此,为了模拟一个具有显著惯性效应的瞬态流动,选择雷诺数为 100 进行优化。但是,这并不意味着如果增加流速,装置的性能会变差。
在 COMSOL Multiphysics® 中进行拓扑优化
拓扑优化可以将一个域划分为固体域和流体域。当使用密度法时,优化是通过内插材料参数来实现的。也就是说固体域被近似看作具有非常低渗透性的海绵。因此,设计变量 0\leq\theta_c\leq1 控制着阻尼力 \mathbf
{F}_\mathrm{Darcy},其定义为
= -\alpha(\theta_c)\mathbf{u},
其中,\theta_c=0 时,\alpha(\theta_c) 较大,对应固体域;\theta_c=1时,\alpha(\theta_c)为零,对应流体域。
由于亥姆霍兹滤波,阻尼可以变得很小,但如果到处都很小,则只能是零。
在实践中,阻尼项不应该完全任意变化,因为这可能会引起不符合物理实际的数值效应。为了限制阻尼项的变化,我们使用亥姆霍兹滤波器引入一个最小长度尺度。(更多信息请参阅之前的博客使用密度方法进行拓扑优化)。
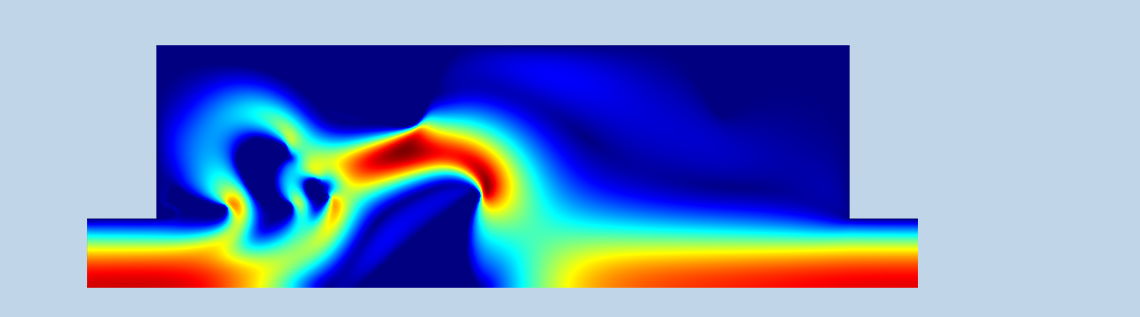
拓扑结构优化的结果如下图所示。可以看到,由于违背了无滑移 边界条件,阻尼项在中央三角形的角落附近不太高。我们可以通过验证研究来探索性能在多大程度上受到这种非物理效应的影响,或者通过增加阻尼或者创建一个没有实体域的新组件。在这种情况下,有限渗透率对性能的影响似乎不大。
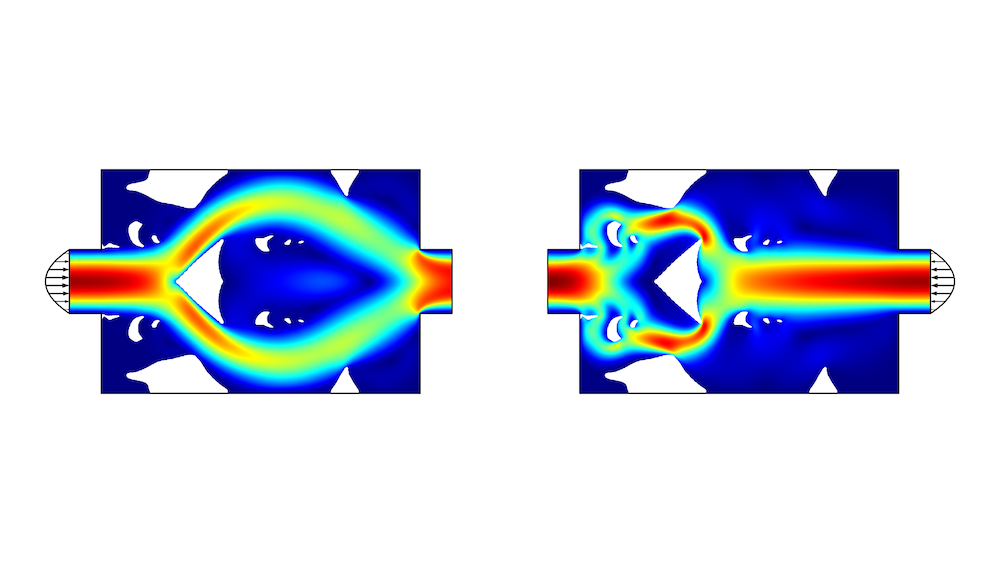
图1.拓扑优化结果用彩色显示,实体区域为白色,流体区域根据流速着色。对于容易流动的方向,流型明显更简单,因此压降比为 2.4。
对特斯拉微阀进行形状优化
拓扑优化的结果有时会非常复杂,也许我们可以做一个更简单的设计,但性能效果与拓扑优化相似,如下图所示。该设计的基本原理与拓扑优化设计相同,其在通道收缩附近有一个中心障碍物。另外,当流体从右边流入时,还有一个自由段将流体引向一个更长的通道。
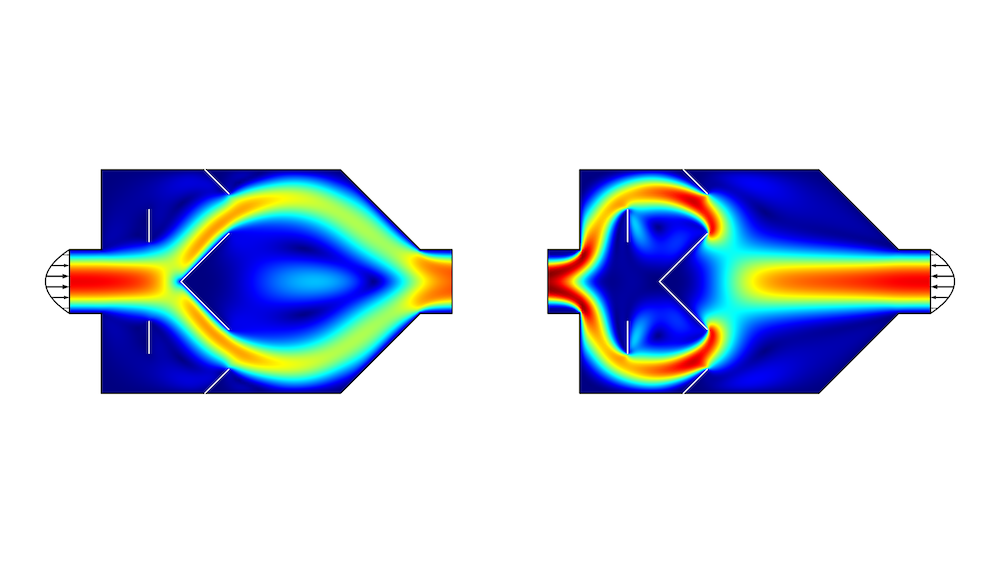
图2.使用内壁(白线)绘制的简单几何图形,其中流速压降比等于 2.3。
COMSOL Multiphysics® 软件支持基于梯度的形状优化,通过固定网格拓扑结构来实现,即只改变网格节点的位置。从 COMSOL Multiphysics 5.5 版本开始,优化模块内置了多个形状优化特征功能,多项式边界 特征就是其中之一。该特征通过平滑方程处理内部节点的变形,而内壁的变形由以下公式给出
其中,d_\mathrm{max} 是最大位移, B_i^n 是 n 阶 Bernstein 多项式的第 i 阶, 0\leq s\leq 1是 COMSOL s 参数。
Bernstein 多项式满足其系数在整个直线上的界限,这意味着直线上的每个点都被限制在一个边长为 2d_\mathrm{max} 的正方形盒子里移动。
如果位移很小,并且使用一阶多项式,那么直线就会保持笔直,移动很小,导致目标函数的改善微不足道。反之,如果最大位移量很大,并且使用高阶多项式,肯定会出现网格质量的问题,所以必须找到一个平衡。下图显示了用二阶多项式进行形状优化的结果,最大位移等于左边内壁的初始长度。
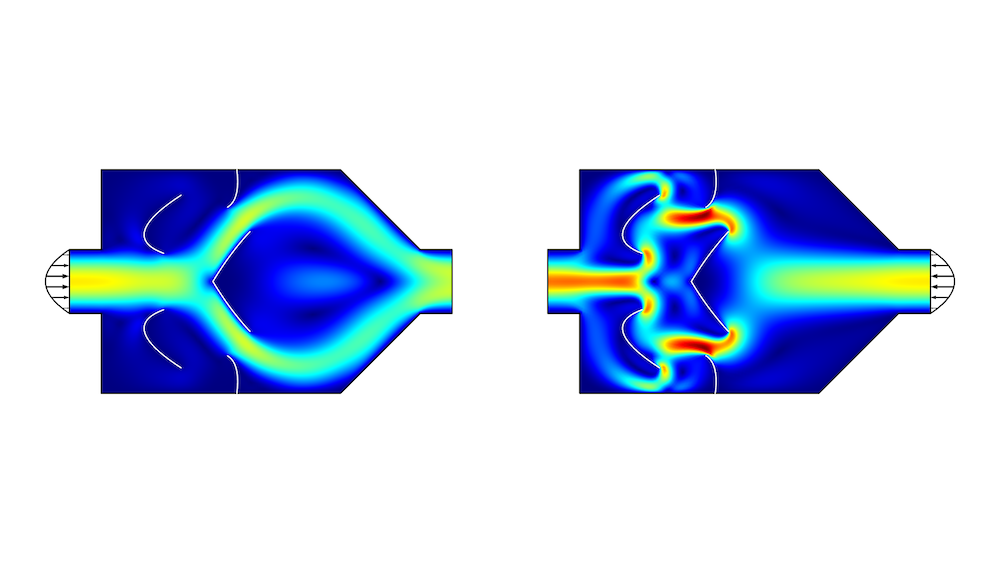
图3.在形状优化后的几何结构中绘制的流速。压降比等于 3.5。
经过形状优化的设计比经过拓扑优化的结果要简单得多(图1),但性能却明显变差。我们可以通过将形状优化的结果作为后处理步骤来改进拓扑优化的结果,例如,特斯拉微阀设计。
与其使用基于梯度优化的内壁,不如创建由实体物体组成的障碍物并应用无导数优化。具体可以参考特斯拉微阀的参数优化教程案例模型。
这个模型以及文中展示的模型都是利用了对称性,但是特斯拉公司的原始特斯拉微阀并不是对称的(参考文献1),所以很自然地我们会想到:是否可以通过消除对称性约束来提高装置性能?你也可能会问,采用压力驱动的流动和优化流速比是否将生成不同的设计?或者形状优化通过引入更多的内壁设计能提升多少性能?提出这些问题很容易,我们也可以使用 COMSOL Multiphysics 轻松找到答案。
下一步
如果您想要了解更多关于 COMSOL 优化模块的功能如何满足您的设计需求,请点击下方按钮。
参考文献
Valvular Conduit, Nicola Tesla, 1920, US Patent 1,329,559.



评论 (5)
Hua Li
2023-07-24May i ask you a question? i make a try to topology-optimize a kind of heat-exchanger(heat conduction coupling laminar flow),but in my topology-optimized result, the liquid domain didn`t connect with each other,even the inlet is full of solid material. i`m confused, have you ever encountered such a problem?how to deal with it?
Kristian Ejlebjærg Jensen
2023-07-24 COMSOL 员工You probably chose interpolation functions which caused that design to become a (local) optimum. It is possible that you can benefit from taking a look at https://www.comsol.com/model/98011.
Hua Li
2023-07-25Thanks so much for your reply, I will take a look at the case and check my settings again.
Hua Li
2023-07-25Another question, please, I also want to extend this kind of topology-optimization to 3D problem. Have you ever topology-optimized the heat conduction coupling laminar flow with COMSOL? Or maybe you use other tools?
Kristian Ejlebjærg Jensen
2023-07-25 COMSOL 员工I am a COMSOL employee, so I do not use other tools. https://www.comsol.com/model/98011 performs topology optimization of heat conduction coupled to laminar flow in 2D. Extension to 3D is conceptually trivial, but in practice one has to use iterative solvers, possibly on a cluster.