
我们经常会遇到关于如何在 COMSOL Multiphysics® 软件中用最佳的方法评估各种应力量的问题,因为软件提供了许多不同的应力变量和呈现结果的方法。在这篇博客中,我们将详细探讨这些问题。在深入讨论应力分析的具体细节之前,我们将重点介绍结果评估的一般方法。
目录
什么使应力如此特别?
在物理学的许多领域,主要关注的量是场本身,而不是其梯度。例如,在传热分析中,我们通常更关注的是温度,而详细的温度梯度和热通量是次要的。而在结构力学中,局部应力和应变往往比位移更重要。在大多数情况下,高应力是静态或疲劳失效的原因。因此,可靠的应力评估很重要。
一些有限元基础
在有限元方法中,几何体被细分为构成网格的小块(称为有限单元)。在每个单元中,都有一个关于要求解的场变化假设,由 形状函数 近似。最常见的是,形状函数是坐标函数的线性或二次多项式。该场可以是标量或矢量。
所有网格单元在网格节点处相互连接。通过考虑某些通量的平衡条件,可以为所有网格节点处的场值建立一个方程组。
下表总结了一些常见情况下要求解的场:
| 物理场 | 场 | 梯度 | 通量 |
|---|---|---|---|
| 固体力学 | 位移(矢量) | 应变(张量) | 应力(张量) |
| 传热 | 温度(标量) | 温度梯度(矢量) | 热通量(矢量) |
| 扩散 | 浓度(标量) | 浓度梯度(矢量) | 质量通量(矢量) |
| 静电 | 电势(标量) | 电场(矢量) | 电位移(矢量) |
在求解通过有限元近似生成的方程时,所有网格节点上的因变量(自由度或 DOF)都是已知的。整个几何结构上的场是连续的,并且单元内任何点的值由单元节点处的值和假设的插值多项式(即形状函数)唯一定义。
然而,在单元之间,场的梯度通常是不连续的。在单元内部,它由形状函数的空间导数和单个单元节点处的节点值确定。因此,在每个单元内,梯度也唯一定义,但在单元边界处不是。然后根据梯度计算通量。对于线性函数,只需要计算梯度与给定材料参数的乘积就可以了。
物理场连续性
重要的是要认识到,由于物理原因,通量大多数时候是连续的。从一个单元流出的东西应该流入下一个单元。只有数值表示是不连续的。然而,随着网格的细化,有限元解将收敛于真实的连续解。不幸的是,对于我们这些从事应力研究的人来说,梯度的收敛速度比场的收敛要慢。
然而,梯度和通量的连续性并不简单。如果两种不同材料之间存在边界,那么只有通量和梯度的某些分量是连续的。
一般来说,通量在边界的法向方向上是连续的,但在切线方向上不是。对于梯度,情况正好相反。
在下面的示例中,研究了由两个具有不同材料属性的正方形组成的矩形中的稳态传热。
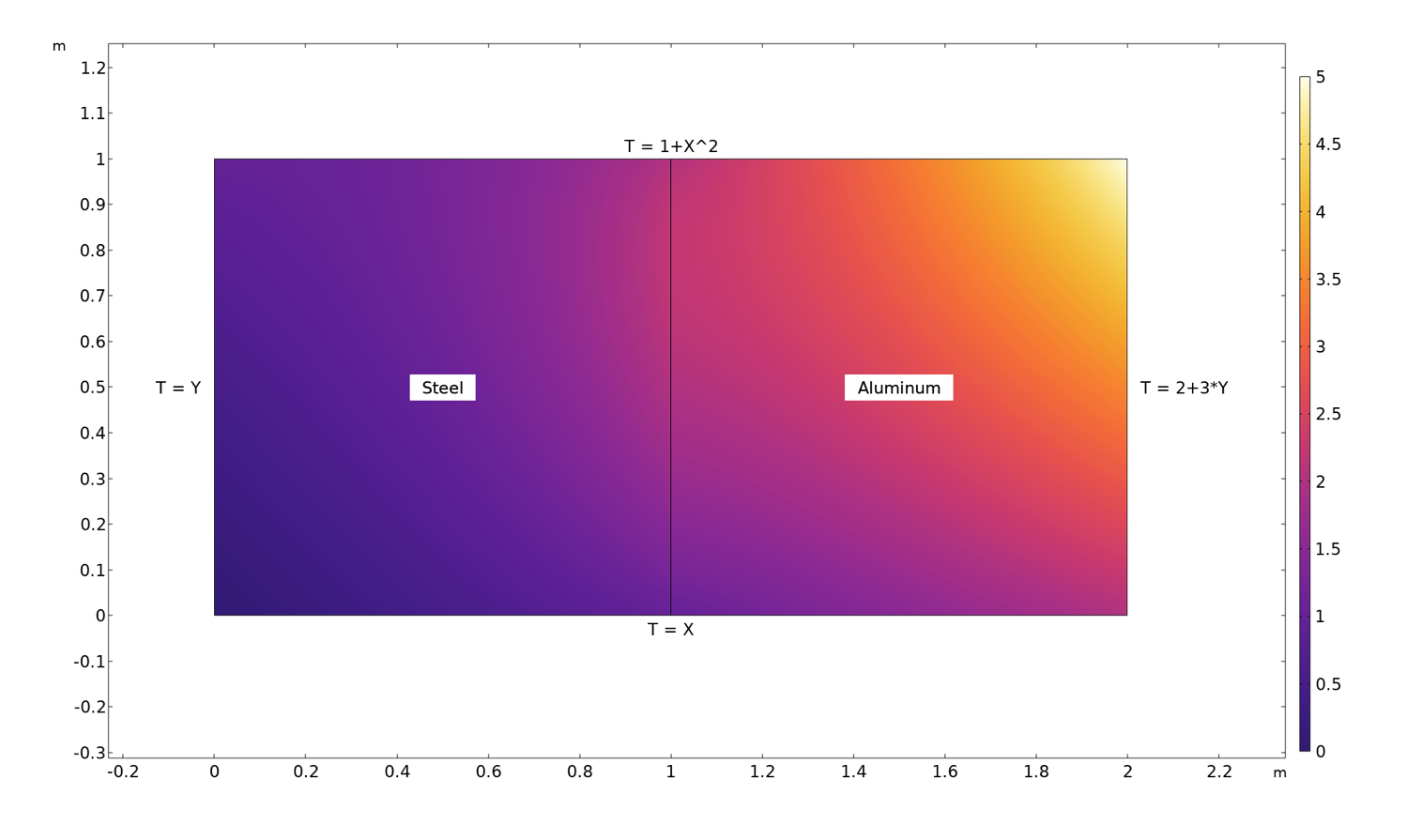
由正方形钢和正方形铝组成的矩形中的温度分布。沿所有边界的温度均为指定值,如图所示。
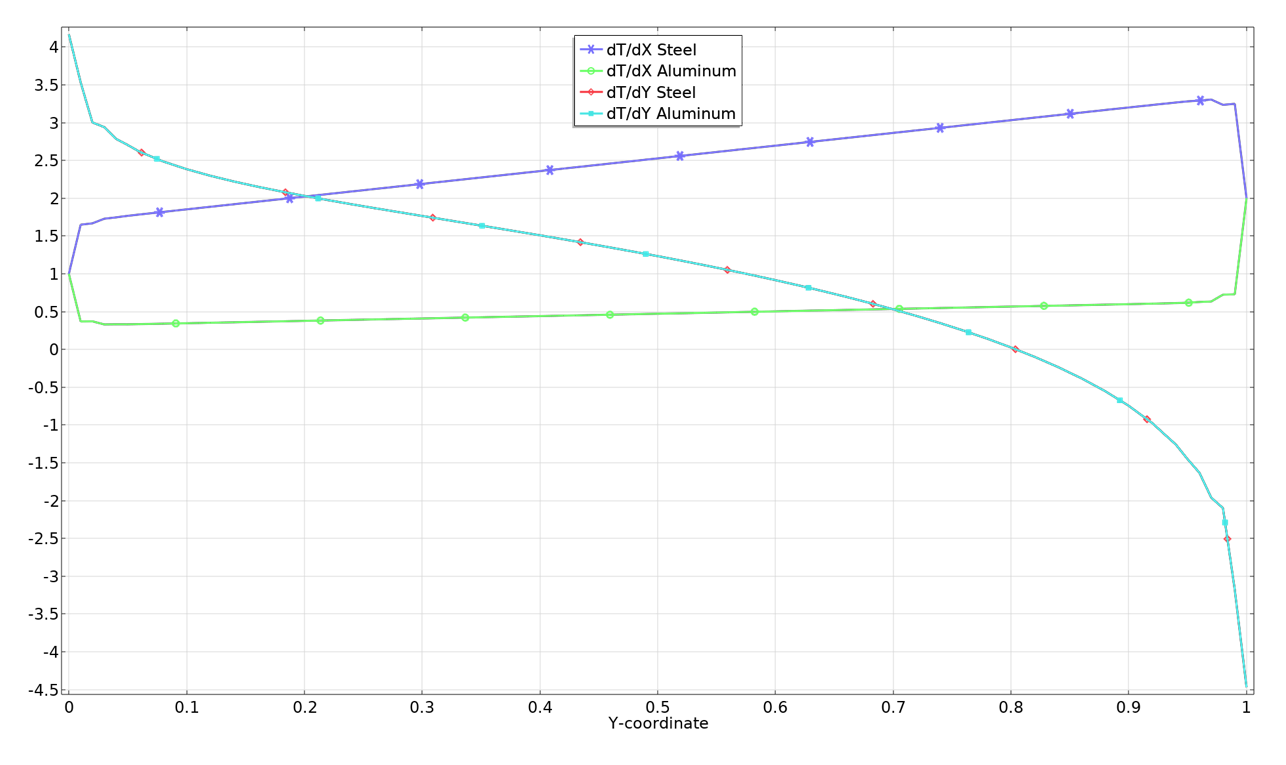
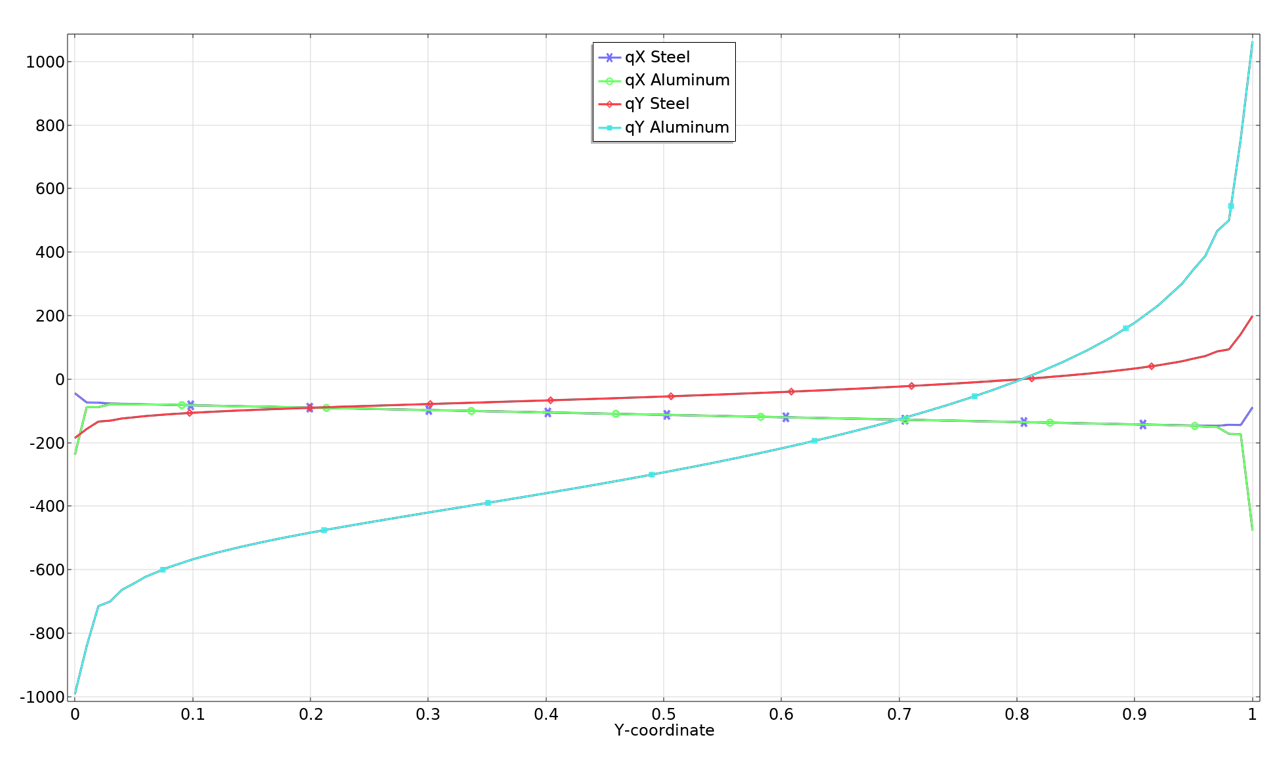
通过绘制沿分隔两个域的边界的温度梯度和热通量,可以直观地显示连续性。
沿材料边界的温度梯度(左)和沿材料边界的热通量(右)。
正如预期的那样,在边界两侧,y 方向的温度梯度以及 x 方向的通量是相同的。如果对固体力学做同样的设定,我们会发现两个应力分量 \sigma_\mathrm{x} 和 \tau_\mathrm{xy},以及一个应变分量 \varepsilon_\mathrm{y} 都连续。另一种看法是,在自由边界上可以指定的通量分量在内边界上也必须是连续的。
请注意,由于组成张量或矢量的所有分量并非都是连续的,像等效应力或通量范数这样的大多数不变量将在材料不连续处出现跳跃。
单元之间的平均
由于我们研究的大多数量都是连续的,因此很容易求取平均值,例如单元之间的应力。这也是大多数情况下的默认设置。通常,这样做不仅会改善视觉印象,而且更接近真正的收敛解。
您可以控制是否以及如何应用平均(或使用结果表示术语:平滑)。重点是对于大多数结果表示,都可用使用 质量 部分。
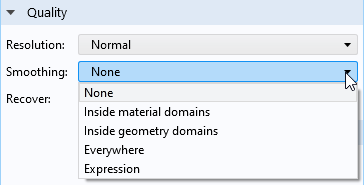
平滑选项。
下表总结了不同的平滑选项:
| 选择 | 影响 |
|---|---|
| 无 | 相邻单元之间没有平滑。 |
| 内部材料域 | 在属于同一材料域的相邻单元之间进行平滑处理。最简单的材料域是一组具有相同材料分配的域。然而,一些物理场接口确实实现了它们自己的定义。例如壳 接口,只有当单元具有相同的材料和厚度并且没有通过折线连接时,它们才属于相同的材料域。请注意,这是添加新绘图时的默认选项。 |
| 内部几何域 | 平滑是在属于同一几何域但不跨越域边界的相邻单元之间完成的。 |
| 所有域 | 在所有相邻单元之间进行平滑处理。 |
| 表达式 | 当布尔、用户定义的表达式计算为非零值时执行平滑。 |
应用平滑时,还可以使用平滑阈值。这格阈值提供了一个限制,即在某个网格节点上相邻单元之间的值差异达到多大时才会禁用平滑。这样做的目的是,在不隐藏明显的不连续的情况下,获得一个总体上平滑的的曲线图。
从 COMSOL® 软件 6.0 版本开始,结构力学接口生成的默认应力图就使用了这个功能。默认情况下,阈值被设置为 0.2,但您可以根据需要自定义此值。
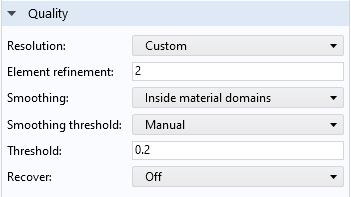
固体力学接口中默认绘图的 质量 部分。使用默认阈值 0.2,可以接受高达 20% 的差异进行平滑处理。
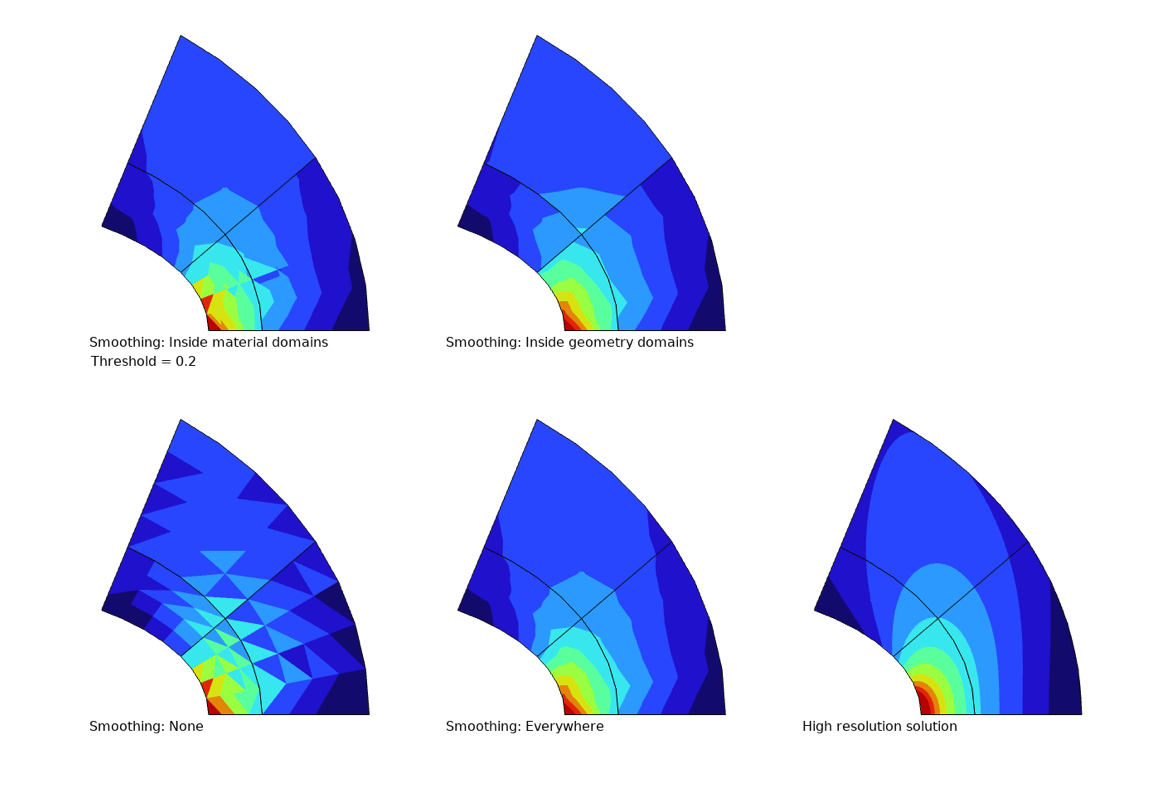
下图显示了在二维单一材料的固体力学模型中的应力图中不同类型的平滑示例。为了强调效果,使用了一阶三角形单元。这是一个低性能的单元,每个单元内的应变和应力都是恒定的。观察这个图时,需要注意的是:
- 在没有进行任何平滑(左下图)处理的情况下,网格中的每个单元都清晰可见。
- 在所有单元之间进行平滑处理后(下中图),视觉印象比没有进行任何平滑处理要好得多。与使用精细网格和二次形状函数生成的“正确”高分辨率解(右下图)的总体相似性并不算太差。然而,高应力区域中的一些细节没有被准确地表示出来。
- 因为在此示例中只使用了一种材料,所以所有域(中下图)和材料域内部选项之间没有区别。
- 当使用内部几何域选项(右上图)时,可以看到域之间的应力跳跃,而平滑处理应用在每个域内。如果为不同的域分配了不同的材料,那么使用内部材料域的图将与此类似。
- 内部材料域选项用于结构力学的默认设置(左上图)。请注意,在应力解析得较差的地方,应力的跳跃清晰可见,而在梯度不太明显的地方,等值线是平滑的。使用这种类型的绘图,可以获得两全其美的效果:总体上看起来流畅,而分辨率不足的区域也十分明显。
到目前为止,我们已经研究了体积图、曲面图和等值线图中的平均和跳跃会发生什么。对于线图来说,复杂性会增加。如果直线有一个或多个相邻曲面,则需要在两个方向上进行平均:
- 沿直线方向,与线是否连接到一个或多个表面无关。方法与上述相同,并且可以使用相同的 质量 设置部分。
- 穿过线方向,如果有多个表面,则在相邻表面之间。首先执行该操作,并且是无条件的。
如果要绘制的量不应该是连续的,就不再需要平均值;如果需要在每个边界 (3D) 或域 (2D) 绘制一个图形,就需要使用特殊的算子。
如果该线表示 2D 中的边界,则可以使用 up() 和 down() 算子指定从哪个域获取结果。“上”和“下”分别对应于法线向量在边界上的方向。上述热通量的图就使用了这个方法。下图是在 x 方向重复的温度梯度,也包括默认的平均结果。显然,当跨越边界存在物理不连续性时,默认平均不是一个好的选择。
同样的技术也可用于 3D 内部边界上的曲面图,但在这种情况下,当然只能一次从一侧绘制值。
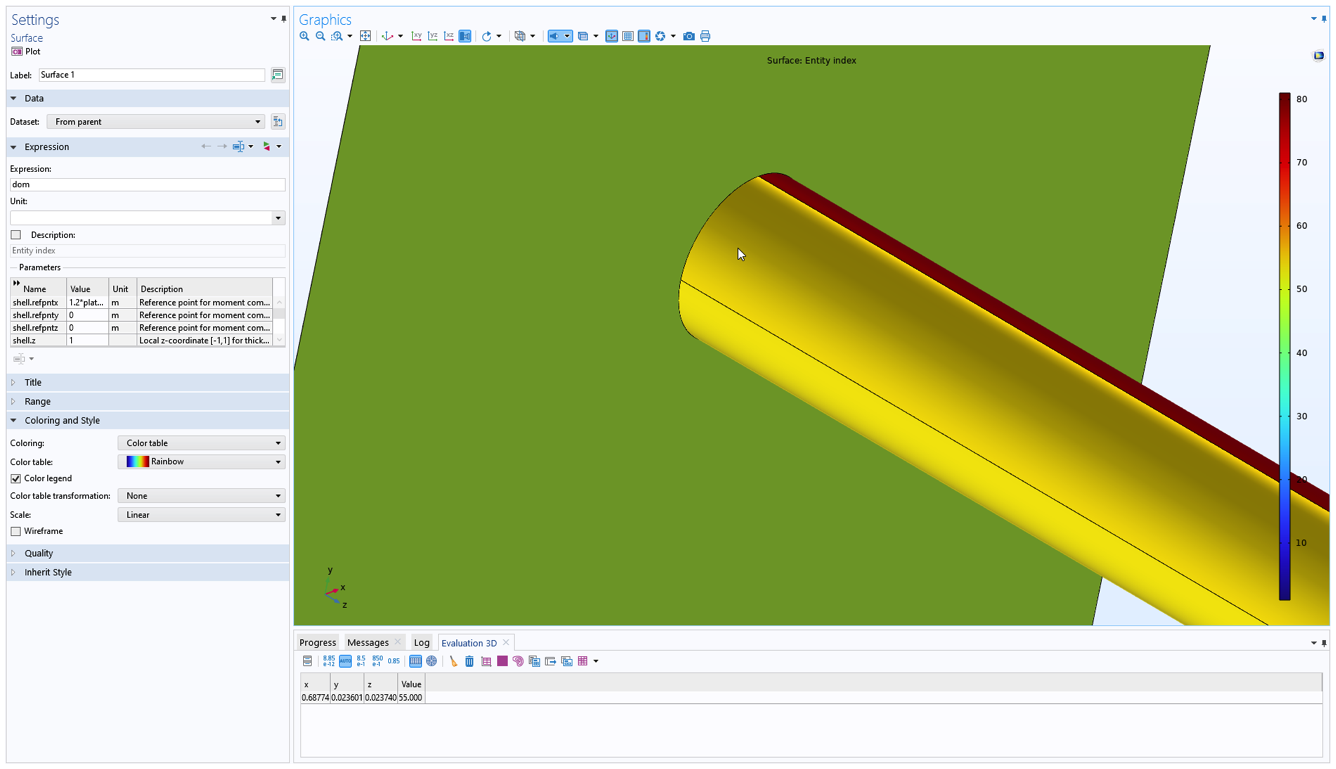
如果所选的线是 3D 中的一条边,情况就稍微复杂一些,因为共享这条边的边界是任意数量的。在这种情况下,您需要使用 side() 算子从各个边界中选取值。边算子的语法类似于 side(12,shell.mises),其中第一个参数是边界数。因此,您首先必须弄清楚您需要结果的边界数。一种快速的方法是创建内置变量 dom 的曲面图,然后只需单击预期的边界即可查看其数量。
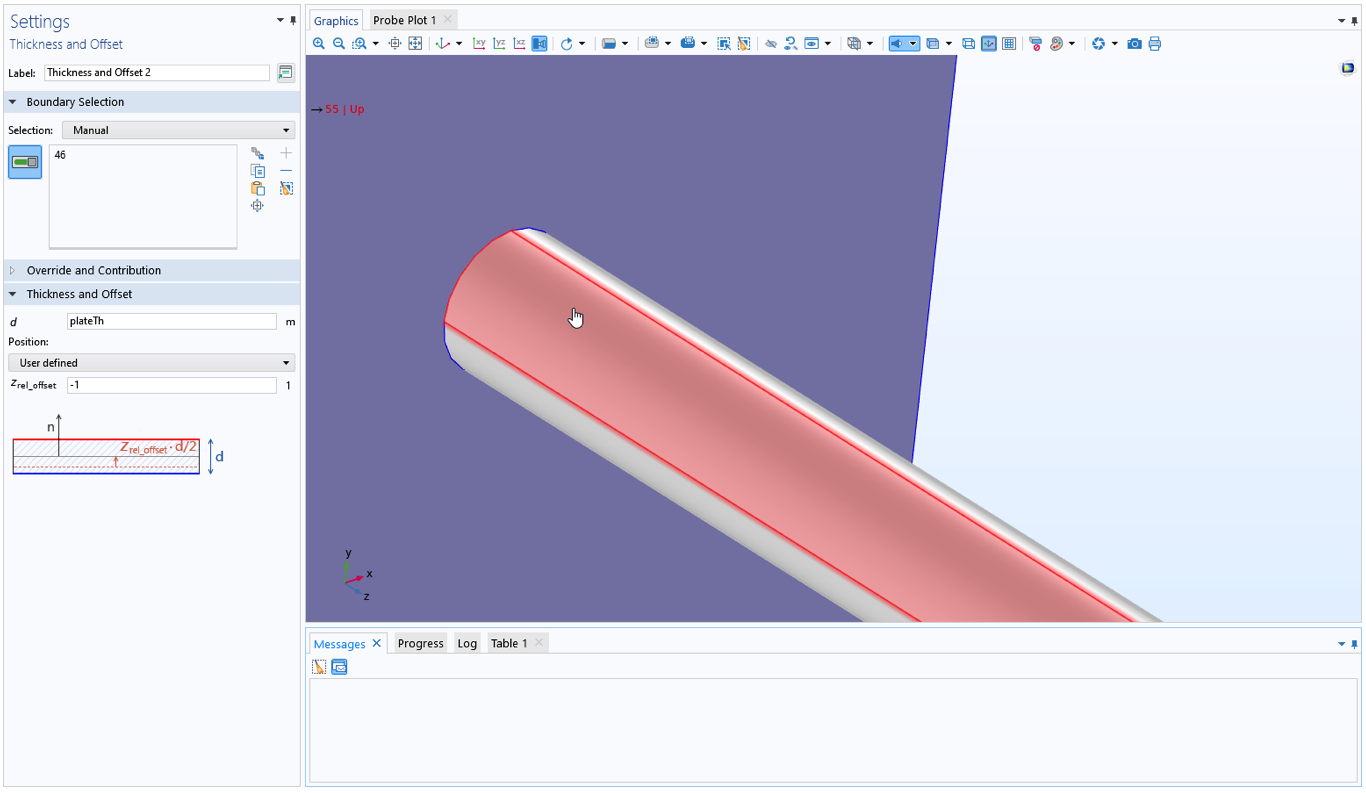
另一种查找边界数量的方法是移动到模型开发器树中具有边界选择的任何节点,然后将鼠标指针悬停在边界上。边界编号动态就会显示在 图形 窗口的左上角。
结果在哪里评估?
生成彩色图和折线图后,通常需在每个单元、单元边界或单元边内的几个点处对要绘制的表达式进行评估。评估点的数量由 质量 部分中的 分辨率 设置控制。
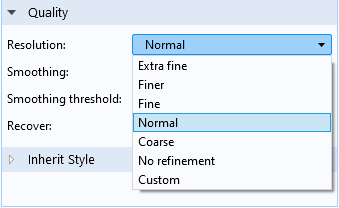
选择分辨率的选项。
当选择了其中一种预定义的分辨率后,将评估的点数取决于几个因素,如模型大小和空间维度。使用高分辨率通常会在单元内生成更详细的图。但是,这仅在评估的表达式在单元内部具有较高的平滑度时才有用。否则,只会产生虚假波动。
如何计算应力
到目前为止,我们主要介绍了一般的结果呈现选项。对于应力的可视化,还有一件事需要考虑,那就是如何在每个单元中实际计算应力。
总应变只是位移的导数,所以总是平滑的。然而,这些应力通常是几种不同效应组合的结果。如何计算应力的确切细节取决于顶层材料模型以及几何非线性是否有效。为了解释一般原理,我们假设顶层材料是线弹性的,并且分析是几何线性的。
那么,应力张量 \sigma, 可以用下式计算
式中,C 是弹性张量,\varepsilon_\mathrm{el} 是弹性应变,\sigma_\mathrm{add} 是任何额外的压力贡献。弹性应变是总应变之差 \varepsilon_\mathrm{tot},使用形状函数和节点位移以及任何非弹性应变场 \varepsilon_\mathrm{inel} 计算。
以下是非弹性应变的一些例子:
- 热应变
- 吸湿膨胀应变
- 塑性应变
- 蠕变应变
- 初始应变
以下是额外应力贡献的一些例子:
- 黏弹性应力
- 阻尼引起的应力
- 初始应力
因此,通常来说总应力是几个不同贡献的总和。尤其是,\varepsilon_\mathrm{tot} 和 \varepsilon_\mathrm{inel} 通常是同一数量级,因此弹性应变张量包含由两个或更多的大数减去另一个大数获得的小数。例如,不受约束的热膨胀或大的塑性变形就是这种情况。
那么为,什么这会是一个问题呢?如果不同的应力和应变贡献不是由单元上相同类型的插值表示,就可能存在较大的局部波动,即使结果在平均意义上是一致的。
一个特例:热膨胀
我们先来研究一个可能发生这种情况的常见案例。有限元界很早就观察到,在耦合热应力分析过程中会出现“波浪状”应力模式。在耦合热应力分析中,最常见的是对位移和温度都使用二次形函数。由于热应变与温度成正比,\varepsilon_\mathrm{inel} 将在每个单元内具有二次变化。然而,由于总应变是位移形函数的导数,因此它将具有线性分布。现在,弹性应变将作为线性函数和二次函数之间的差被计算。产生的影响是每个单元内部可能存在奇怪的弹性应变(以及应力)模式。出于这个原因,当将温度作为驱动固体的热膨胀时,有时建议使用线性形函数来求解热问题。在 COMSOL Multiphysics 中,此问题在内部由 热膨胀 多物理场耦合节点(以及 吸湿膨胀 和 插层应变 等类似功能)处理。非弹性应变场被重新插值到一个与从位移场计算出的应变相匹配的多项式阶数。这将减少局部应力解中的这种假象。
逐点状态
还有另一种类型的非弹性应变根本不涉及场,而是在积分点(高斯点)处逐点的局部状态。有关高斯点的更多详细信息,请查看博客数值积分和高斯点简介。大多数非线性材料模型,如塑性和蠕变,都是这样工作的。在这种情况下,单元中任意位置的应力评估会变得更加复杂。
如果要求一个应力分量,例如 solid.sx,它实际上是在单元中的每个位置“动态”计算的。非线性材料定律就是在该位置利用最近的 高斯点的存储值被评估的。如果单元上非弹性应变的变化很大,可能会引入明显的误差。甚至可能无法评估材料定律,即使它可以在高斯点进行评估。
一个比较好的方法是基于高斯点值创建平滑近似。gpeval() 算子提供了这种可能性。例如,如果您请求 gpeval(4,solid.sx) 而不是 solid.sx,您将绘制一个在单元上平滑的应力。在这种情况下,非线性应力-应变关系仅在已经满足的高斯点处进行评估。然后,再使用高斯点值的最小二乘拟合来定义平滑场。
在其原始版本中,gpeval() 算子要求输入适当的积分阶次作为第一个参数。幸运的是,在大多数情况下,不必这么做。COMSOL 软件的物理场接口中提供了许多预定义变量,例如 solid.sGpx 和 solid.misesGp。如果无法为表达式找到合适的内置变量,则可以使用物理场接口的特定算子,例如 solid.gpeval(expr)。 正确的积分阶次将被嵌入到特定物理场接口的算子中。
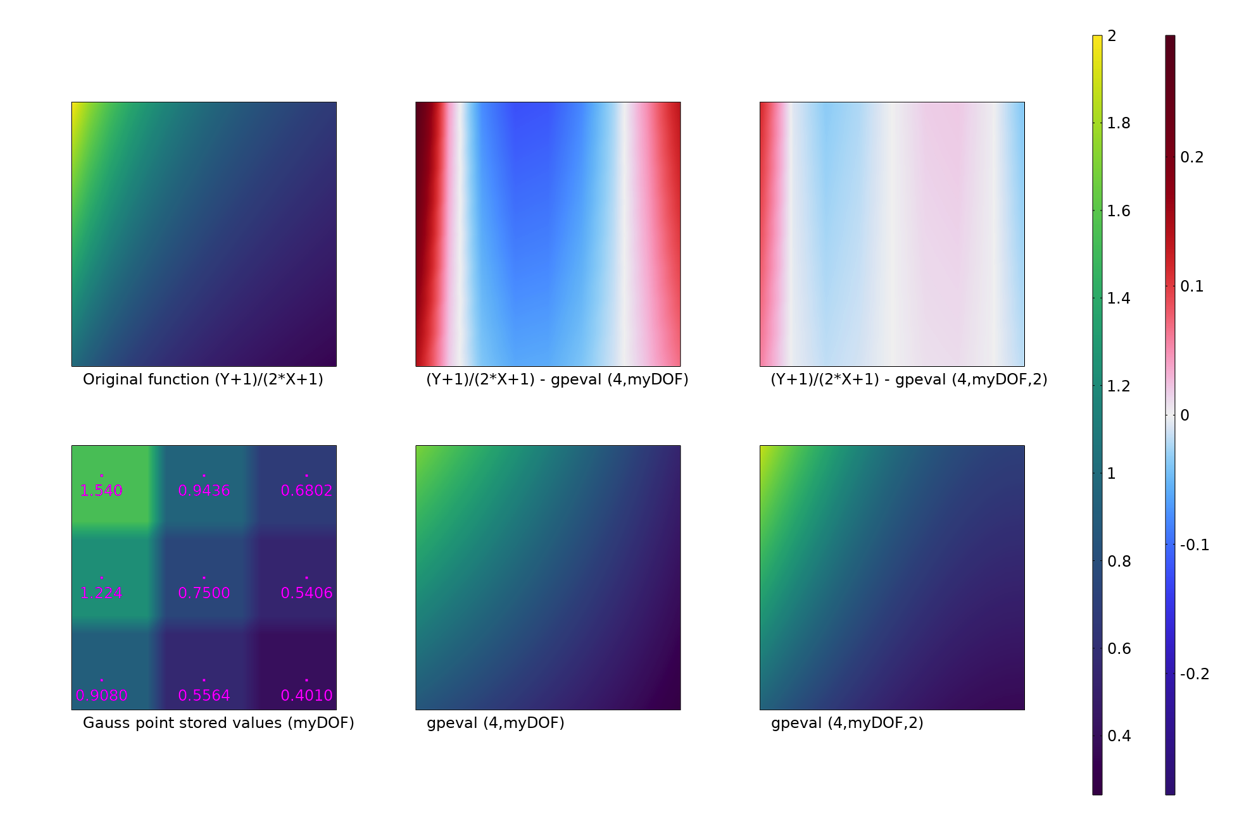
下面的示例针对已经存储在高斯点的场(通过名为 myDOF 的用户定义的因变量)探索了不同的评估选项。该模型由单个 2D 单元组成,x 和 y 坐标范围为 0 到 1。该场由表达式 (Y+1)/(2*X+1) 描述。使用 3 × 3 高斯点方案,因此将存储九个独立的数字。这些值正是在每个高斯点处评估的原始场的值。
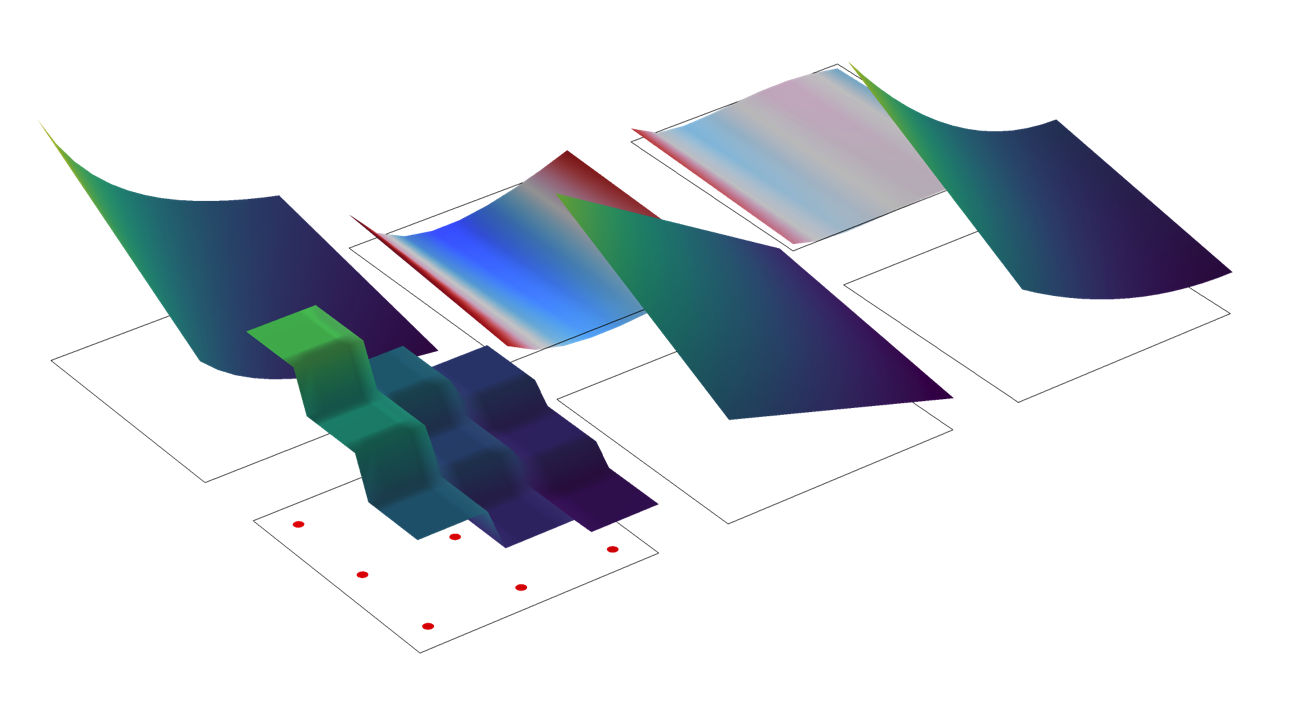
用高度图表示的同一组数据。
在图中左上方,原始函数是可视化的。在它的下方,显示了存储状态 myDOF 表面图的行为。此图中也显示了高斯点的位置以及存储的值。默认的行为,即高斯点状态由最近的高斯点处的值表示,在这里清晰可见。在这种情况下,一个更好的方法是使用 gpeval() 算子评估平滑场,如底行最右边的两个图所示。这两个图之间的差异是平滑场的多项式阶数。默认是使用双线性场(中下方)。在这个示例中,拟合二次场是更好的选择。在图的中上方和右上方,显示了平滑场与函数精确值之间的差异。
最后,我们来处理两个常见的误解:
- 如果在高斯点处评估一个类似于
solid.sx的表达式,确实会在高斯点处获得计算值。但是,在高斯点处评估类似于solid.sGpx或gpeval(4,solid.sx)的表达式将不会在该点检索存储的结果。原因是这些表达式给出了通过最小二乘拟合获得的平滑场。拟合多项式不一定会通过其数据点。 - 如果在边界上评估一个类似于
gpeval(4,solid.sx)的表达式,则 边界上高斯点的值用于设置插值多项式。如果在固体力学模型的边界上绘制表面图,这可能不是想要的结果。幸运的是,COMSOL 软件接口中内置的solid.sGpx和solid.gpeval(solid.sx)与期望的一样:它们使用域插值。
最大值评估
有了上面介绍的方法,我们就可以处理一些评估最大值的常见任务。首先,重要的是要认识到没有单一的“正确”方法。唯一的真理是使用非常精细的网格进行分析,以使离散误差尽可能小。在现实生活中,这是不太可行的。
话虽如此,通常最好使用高斯点插值结果,因为不太容易出现随机波动。然而,对于所有情况,这可能不是最好的结果(在“最接近真相”的意义上)。
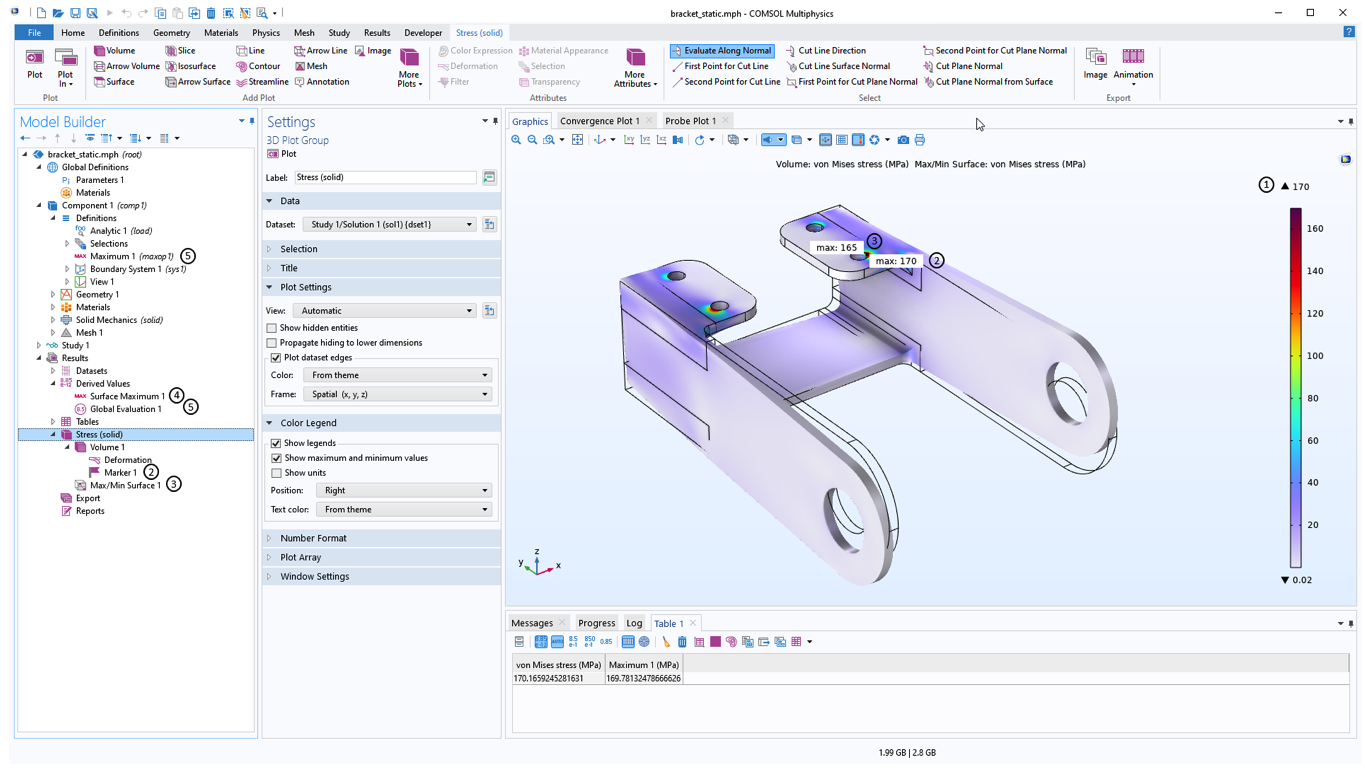
在结果与可视化中,可以使用不同的方法来获得最大值(下面的UI截图中显示了其中的五种)。您可以查看图例上的最大值(见下图(1)),也可以添加:
- 标记 子节点,例如,体积图(见(2))。
- 标记 子节点使用与绘图本身相同的数据进行,因此结果始终一致。
- 由绘图的 质量 部分的设置控制评估。
- 像 表面最大值/最小值 这样的节点到一个绘图组(参见(3))。
- 这些节点有自己的设置。
- 在 高级 部分进行控制评估。
- 派生值 下的类似 表面最大值 的节点(参见(4))。
- 这些节点有自己的设置。
- 在 配置 部分控制评估。
- 定义 节点下的 最大值 算子(参见(5))。
- 这类算子有自己的设置。
- 在 高级 部分控制评估。
- 该算子可用于 全局评估。
- 线图的 图形标记。
- 使用与绘图本身相同的数据评估标记,因此结果将始终一致。
- 由绘图的 质量 部分的设置控制。
- 派生值 下的 点计算 节点——如果已知临界点。
- 几何点将使用相邻边、边界或域的平均值。
- 截点 数据集中的一个点将从单个单元的单个评估中获取其值。
很明显,使用这些方法获得的值不一定相同。以下是一些提示:
- 如果要突出显示绘图或图形中的峰值,请使用相应的 标记 子节点。如果值不一致,查看绘图的人会感到困惑。
- 如果想获得最坏情况下的值,请使用抑制平均的评估。
- 只要使用平滑或应力计算涉及到逐点状态,表面和体积最大值评估可能不会给出相同的值,即使预期最大值在表面处。
- 对于结构力学问题,最大应力通常出现在边界处。如果边界没有加载,有一个很好的技巧可以获得准确的结果,就是在它上面添加一个非常薄的膜,其材料数据与实体相同。这个膜充当一种虚拟应变计。
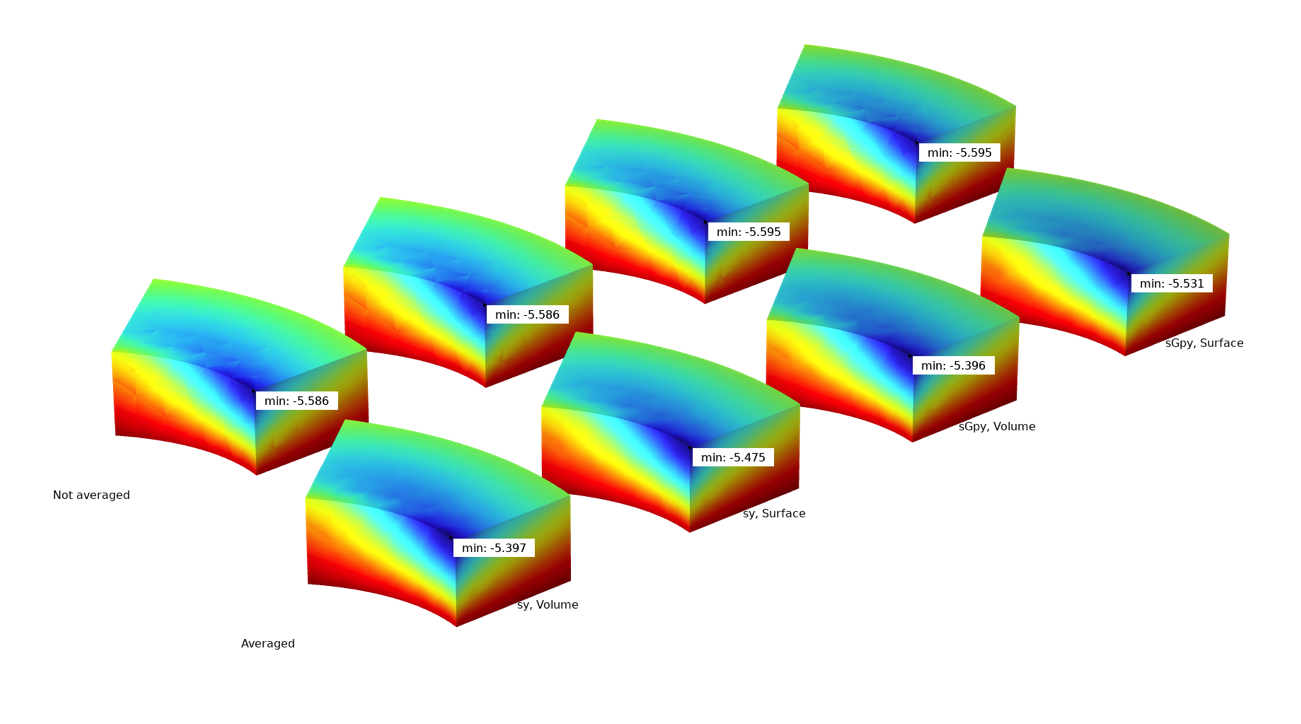
下图显示了使用不同的方法评估应力分量最小值的效果,通过表面图和体积图标记。solid.sy 和 solid.sGpy 都使用了平均和不平均绘制。正如预期的那样,未经平滑计算的每个值都高于经过平滑计算的相应值。还可以注意到,如果没有平均,表面和体积评估会给出相同的结果。这是很自然的,因为峰值在表面,所以在两种情况下都探测到相同的峰值位置。
我应该绘制哪些应力结果?
当您要选择绘制结果时,会遇到如下所示的菜单:
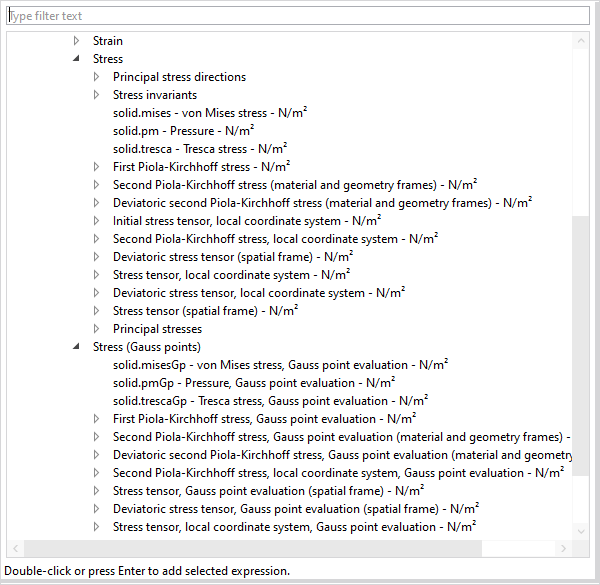
选择应力结果。
可选择的方法取决于物理场接口以及使用的材料模型和其他选项。这可能看起来令人不知所措,但有些量比其他量更重要。
对于各向同性材料,最常见的是使用标量应力测量,例如 von Mises 或 Tresca 等效应力。von Mises 应力很受欢迎,因为它很容易评估,并且它可以直接计算灵敏度。但是,为安全起见,Tresca 压力是更好的选择。Tresca 等效应力的值比给定应力状态下的 von Mises 应力值大 0% ~ 17%。在某些工程领域,如压力容器,常用的是 Tresca 应力,有时称为 应力强度。
尽管 von Mises 和 Tresca 等效应力对于了解应力状态非常有用,但它们只能用于评估失效风险或找到特定材料类别的“最大负载点”。这些应力测量最初是为预测金属的屈服而设计的,它们对平均应力不敏感。金属在太平洋海底中并不比在自由空气中更接近屈服!另一方面,土壤或混凝土等材料的失效很大程度上取决于平均应力。压缩状态是稳定的。
现在你可能会问:如果我的材料不是金属,我怎样才能得到一个以红点为临界点的图?答案包含两个部分:首先,如果不引入一些描述失效的材料属性,通常不能这样做。一旦您可以访问这些值,就可以使用结构力学接口中的 安全 节点。这个功能可以为许多类别的材料计算不同类型的失效裕度测量值。由于这些标准通常基于压力,因此上述关于压力评估的任何内容也适用于此。
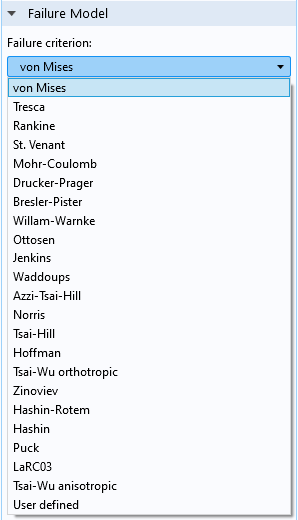
安全特征 中的失效模型。
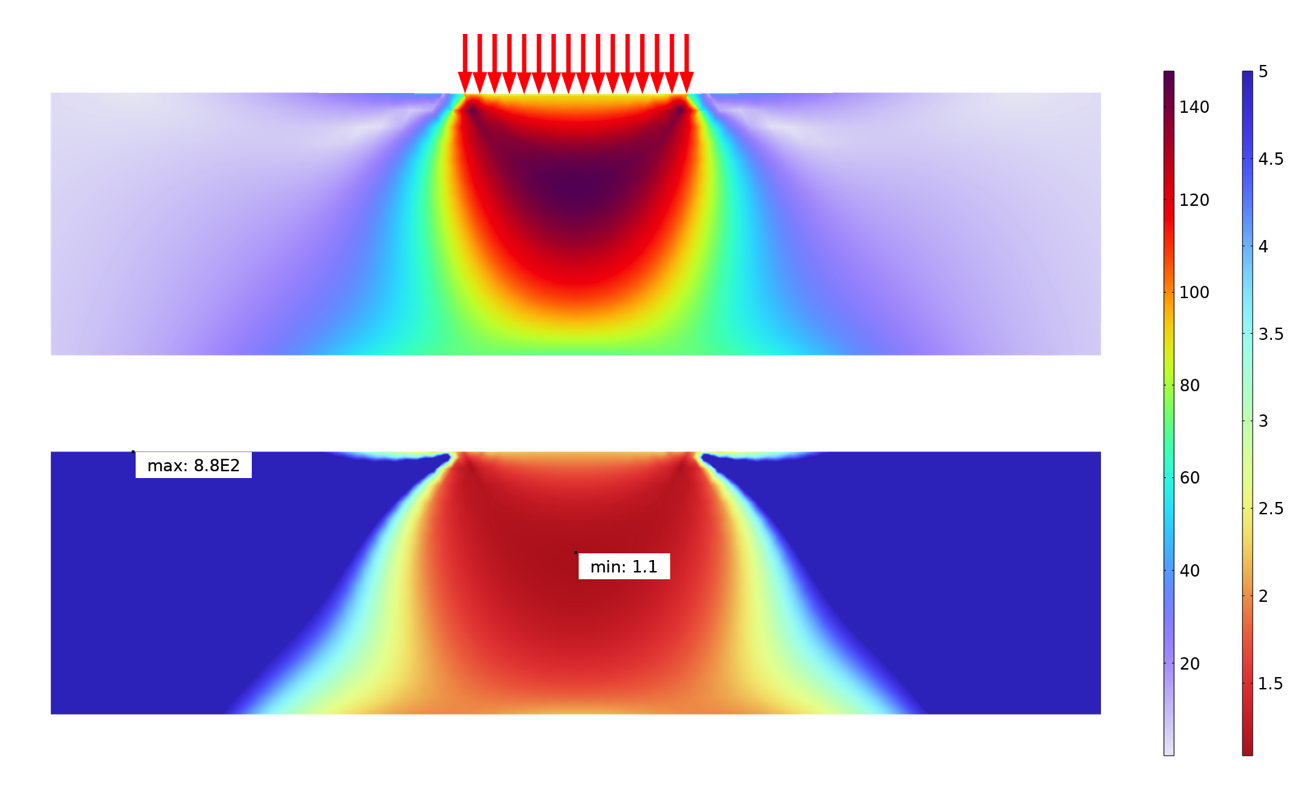
土力学问题的 von Mises 应力(上)和安全系数(下)分析。下面的分析使用了 Drucker-Prager 标准。
有时,您可能会因为材料是各向异性的,或者想更好地了解应力分布而研究各个应力分量。对于后一种情况,绘制主应力图通常也很有用。
在处理单个应力分量时,您希望在全局坐标系之外的其他方向上进行评估是很常见的。有几种标记为“局部坐标系”类型的结果。这意味着方向是由材料节点中的坐标系选择确定,例如 线性弹性材料。
在材料模型中选择坐标系。
对于各向同性材料,坐标系选择的唯一作用是为结果定义局部方向。对于各向异性材料,选择的主要目的是为材料数据提供参考方向。附带的您会在局部方向上得到应力和应变结果。
在 COMSOL Multiphysics 中,存在三种类型的应力张量:柯西、第一类皮奥拉-基尔霍夫,第二类皮奥拉-基尔霍夫。要了解有关此主题的更多信息,请查看博客:为什么会有这些压力和应变?以及 COMSOL 官网上关于应力和运动方程的多物理场百科知识。如果您计划研究应力张量的单个分量,区别可能很重要,但对于几何线性分析,应力张量都是相同的。
结语
COMSOL Multiphysics 为精细调整结果的评估和展示提供了多种方法。为了充分利用仿真,熟悉这些方法很重要,什么是最佳选择取决于您正在研究的内容和分析的目的。
还有一种我们没有讨论的情况是,如何处理出现在拐角处或其他奇点处的高应力。博客“有限元模型中的奇点:如何处理模型中的红点” 中讨论了奇点的影响。后续我们可能会重新讨论这个有重大实际意义的话题。
下一步
想要进一步了解 COMSOL 软件的应力分析功能吗?请点击下方按钮联系 COMSOL!




评论 (0)