电磁学稳态电流

电流守恒

电流守恒是自然界的基本定律，用方程形式可以表示为

⁽¹⁾

其中，是电流密度矢量，是空间电荷密度。
在稳态电流或直流电（DC）这些重要的特殊情况下，下式成立

⁽²⁾

因此，直流电流的方程为

⁽³⁾

这个方程在数学上类似于自由空间中的静电方程。另外，就像静电情况一样，麦克斯韦方程组暗示了电场需要满足无旋（无旋度）场的额外要求。

⁽⁴⁾

这是在稳态电流理论中没有电磁感应的另一种说法。

欧姆本构定律的材料

电流密度与电场成正比的材料可以用称为欧姆定律的本构方程描述

⁽⁵⁾

其中是电导率，表示如下

其中，分别表示电荷载流子的迁移率、数密度和电荷，因此电流密度可以改写为

其中，是电荷载流子的漂移或平均速度。

在铜线等导体中，电荷载流子（电子）的漂移速度低至每秒几微米，明显小于电能的流速（接近光速）。

在各向异性材料情况下，电导率可以是一个 3x3 的张量

⁽⁶⁾

这意味着，对于某些材料来说，场和电流密度矢量可能不会完全一致。

欧姆定律通常适用于金属等良导体，其电流主要由电子携带。对于半导体材料的绝缘体，欧姆定律可能是不够的，需要更高级的模型。

借助电势，用欧姆定律描述的材料中稳态电流的基本方程可以变为

⁽⁷⁾

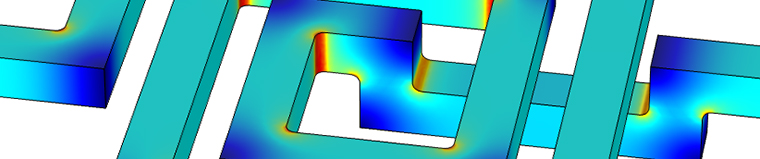
螺旋电感器中的电流密度，其中左右边界之间施加了电势差。左图显示电感器表面的电流密度幅值，右图显示切割结构的截平面上的电流密度幅值。蓝色和红色分别表示低值和高值。右图中的箭头表示电流密度的方向，电流趋向于流经最短路径，如该结构内角处的红色区域所示。

材料界面的稳态电流方程和边界条件

稳态电流理论与静电学理论相似。下表汇总了最重要的稳态电流方程：

方程名称	微分形式	积分形式	边界条件
电流守恒
法拉第定律（稳态电流）

法拉第定律在稳态电流理论中的含义与静电学中的相同。电流守恒方程的含义可以概括如下：

方程名称	微分形式	积分形式	边界条件
电流守恒	电荷不能被创造或消灭	通过封闭表面的总电流等于零；这是电路的基尔霍夫电流定律的等效场	电流密度的法向分量是连续的

稳态电流产生的磁场

上述关于稳态电流的理论不涉及任何磁场；然而，稳态电流总会产生磁场。由于磁场是静止的，因此不会产生任何二次电流（涡流），一旦知道了稳态电流，就可以完全确定磁场。例如，您可以根据麦克斯韦-安培定律的稳态版本来计算由稳态电流产生的磁场

请注意，通过取这个方程的散度，电流守恒方程可以恢复到它的稳态形式

功率损耗和电阻损耗

对于体积，以场量表示的功率损耗为

其中，功率能量密度定义为

在导体中，这种功率被转化为热量，称为电阻或欧姆损耗。

---

发布日期：2021 年 1 月 15 日
上次修改日期：2021 年 1 月 15 日