应力和运动方程
应力和运动方程简介
当固体发生变形时,材料中会出现内力分布,这种力称为应力,它是单位面积上的力。
在横截面A受轴向力F载荷作用的杆中,力方向的应力为。在日常生活中,我们可以观察到,越厚的物体能承受的力越大。因此,应力是一个非常直观的物理量,它可以反映材料负载程度的相关信息。
除了上图所示的这种非常特殊的情况以外,整个承载体的应力大小和方向都会发生变化。

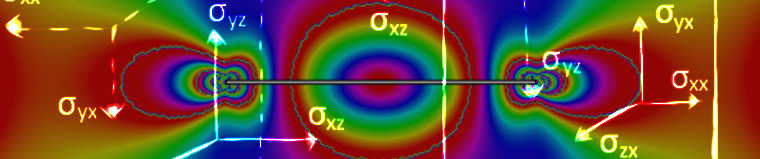
通过实验确定的软材料中刚性物质周围的应力分布。该图片由 SSMG-ITALY 提供,是用光测弹性学方法生成的,已获CC BY-SA 3.0授权,通过Wikimedia Commons共享。
通过实验确定的软材料中刚性物质周围的应力分布。该图片由 SSMG-ITALY 提供,是用光测弹性学方法生成的,已获CC BY-SA 3.0授权,通过Wikimedia Commons共享。
当力垂直作用于表面时产生的应力称为正应力;沿切向作用于表面的力所引起的应力称为剪切应力。
动量平衡
根据牛顿第二定律,体的内力(如应力)必须与外力和惯性力保持平衡。
我们设想这样一个小表面,其中的质点在整个变形过程中保持不变,并假设变形不会导致材料失去连续性,因此也不会产生裂纹。在发生变形之前,该表面的面积表示为dA,法矢为N;在变形后,分别变为da和n。这个表面不一定是体的外表面,也可以是体内任意位置的纯概念表面。
作用在变形区域上的表面力可以表示为
其中,tn称为牵引力,而TN通常称为标称牵引力,原因是它将实际变形状态下的作用力与未变形区域关联起来。
牵引力是单位面积上的力。如果在变形过程中面积发生了变化,则两个牵引矢量的大小不同,但方向相同。
我们可以使用牵引力的空间分量Ti来表示标称牵引力,并用其材料分量NJ来表示法矢。有关空间坐标系和材料坐标系的讨论,请参阅变形分析页面。
此外,我们还可以基于法矢将牵引分量写为以下线性展开式:
在此处和下文中,假设对重复指标求和。空间分量和材料分量分别使用小写和大写字母。
这种表示有时称为柯西定律或柯西公式,仅适用于PiJ为特定二阶张量的分量的情况。
对于任意未变形的材料体积V0,动量守恒可以用以下积分形式表示:
其中,表示体积力,如重力或离心力,速度场根据位移场
计算为
。
根据散度定理,使用柯西公式可以将表面积分转换为体积积分:
由于体积任意,因此可以得到动量平衡方程的微分形式如下所示:
或者使用张量符号得到:
张量P称为第一类 Piola-Kirchhoff应力张量,它将空间方向的作用力与原始未变形构型中的区域关联起来。因此,它的分量指标涉及不同的构型。有时,这种数学对象称为两点张量。一般来说,这个张量不对称。
在实际的变形构型中,可以对牵引矢量tn和材料体积应用类似的方法,由此,矢量可用下式表示:
张量称为柯西应力张量或真实应力张量,原因是它表示与实际变形区域相关的实际构型中的力。该张量由其空间分量表示。
我们设想这样一个小区域,其法矢与一个空间坐标轴(例如,第三轴)平行,此时柯西应力张量分量的含义会变得非常明确。由此可得该区域的法矢为 {0,0,1},并且牵引力可由下式给出
如此一来,具有 33 个指标的应力张量分量可以给出平面上第 3 个方向(平面法向与此相同)的牵引矢量分量。具有两个相等指标的应力张量分量称为正应力。另外两个应力张量分量提供与平面相切的牵引力部分,这种分量称为剪切应力。
通过对一个小立方体取力矩平衡,可以看出柯西应力张量是对称的,因此得到,只要没有体积矩作用,这个等式就成立。尽管这种材料并不常见,但确实存在,可以通过Cosserat 理论进行分析。
由于柯西应力张量和第一类 Piola-Kirchhoff 应力张量对同一个表面力有着不同的表示,
要确定这两种应力测量方式之间的关系,我们可以使用Nanson 公式计算变形引起的面积变化,表示为
其中,F为变形梯度张量,由此可得
体积因子J可以给出变形引起的体积变化。因此,应力张量可通过下式与之关联
通过引入一个称为基尔霍夫应力张量(定义为)的张量,可以进一步简化这个公式及类似公式。基尔霍夫应力张量是一个几乎没有实际用途的物理量,但却具有理论上的便利性。
质量守恒和欧拉公式
根据柯西应力张量,动量平衡方程可以写为
请注意,方程中的密度表示已变形材料的真实密度。此外,体积力为单位变形体积上的力。由于质量守恒,密度与变形隐含相关
从计算的角度来看,引入的非线性降低了这种动量平衡方程形式的关注度。
通过使用速度并基于x=x(X, t) 将自变量转换为空间坐标,可以得到
这就是欧拉公式中的动量平衡。这种公式通常用于流体动力学,其中使用速度作为因变量。
机械能平衡
将动量方程的微分形式乘以速度矢量,并基于材料对其进行积分,可以得到以下方程:
这个方程给出了机械能平衡的积分形式,也称为幂定理。速度的空间梯度为,其中的 : 运算符表示对两个指标求和;
。变形分析页面对速度梯度的特性进行了详细论述。
方程右侧的两个积分项分别表示体积力和表面力的功率输入,它们分别是这些力在每单位时间内对材料所做的功。
左侧的项分别为动能变化率以及为体提供的应力功率。对于弹性材料,应力功率是应变能密度变化率。
通过使用以下关系式
应力功率可以表示为以下等价形式:
因此,我们得出这样一个结论:第一类 Piola-Kirchhoff 应力张量和变形梯度形成了能量共轭对。这种共轭对也可以称为功率共轭或功共轭应力和应变测度。
速度梯度可以分解为对称和反对称部分,分别称为应变率张量(Ld)和自旋张量(Lw)。由于柯西应力张量是对称的,,因此,与柯西应力形成功率共轭的应变测量是应变率张量。后者也可以写为
其中
为格林-拉格朗日应变张量。由此,应力功率积分可以改写为:
其中
称为第二类 Piola-Kirchhoff应力张量,这是一个对称张量,与格林-拉格朗日应变形成能量共轭。
第一类和第二类 Piola-Kirchhoff 应力张量通过下式相关:
基于此公式,我们可以将动量平衡方程改写为:
再结合以下形式的本构关系
可以形成位移矢量的封闭方程组。
旋转平面上的应力分量
对于承受轴向载荷的杆,我们很容易将应力看作一个标量,并认为这个杆上只存在正应力。全应力张量为
在x轴与杆的方向一致的坐标系中表示该应力张量的分量,而在任何其他坐标系中,则同时存在正应力和剪切应力。我们设想一个不与杆轴垂直的概念内表面,就能看出这一点。在这个表面上,实际上存在法向(σ)应力和剪切(τ)应力,如下图所示。
在第一轴与表面法线一致的旋转坐标系中,应力张量的结构如下
其中,表示杆轴与表面法线的夹角。
这种应力状态通常称为单轴应力;不过,只有在特定的坐标系中,它才能用单个正应力分量表示。
柯西应力与第二类 Piola-Kirchhoff 应力比较
我们设想一种正交各向异性材料,其中在沿直悬臂梁的特定方向上包含纤维。
由于第二类 Piola-Kirchhoff 应力沿材料方向定义,因此,我们可以通过它将纤维方向的应力可视化,即使结构处于旋转状态也可以执行此操作。
在下图中,由于梁的一端受纯力矩作用,导致梁发生弯曲。我们可以看到柯西应力和第二类 Piola-Kirchhoff 应力的分量 11。由于弯曲应力沿着梁物理定向,因此,与空间固定水平方向相关的柯西应力的分量 11 会随着挠曲的发生而减小。另一方面,第二类 Piola-Kirchhoff 应力沿整个梁(也处于变形构型)具有相同的全厚度分布。
第二类 Piola-Kirchhoff 应力的实际值更难解释,原因是它与原始面积或变形面积都无关。
发布日期:2018 年 4 月 19 日上次修改日期:2018 年 4 月 19 日
