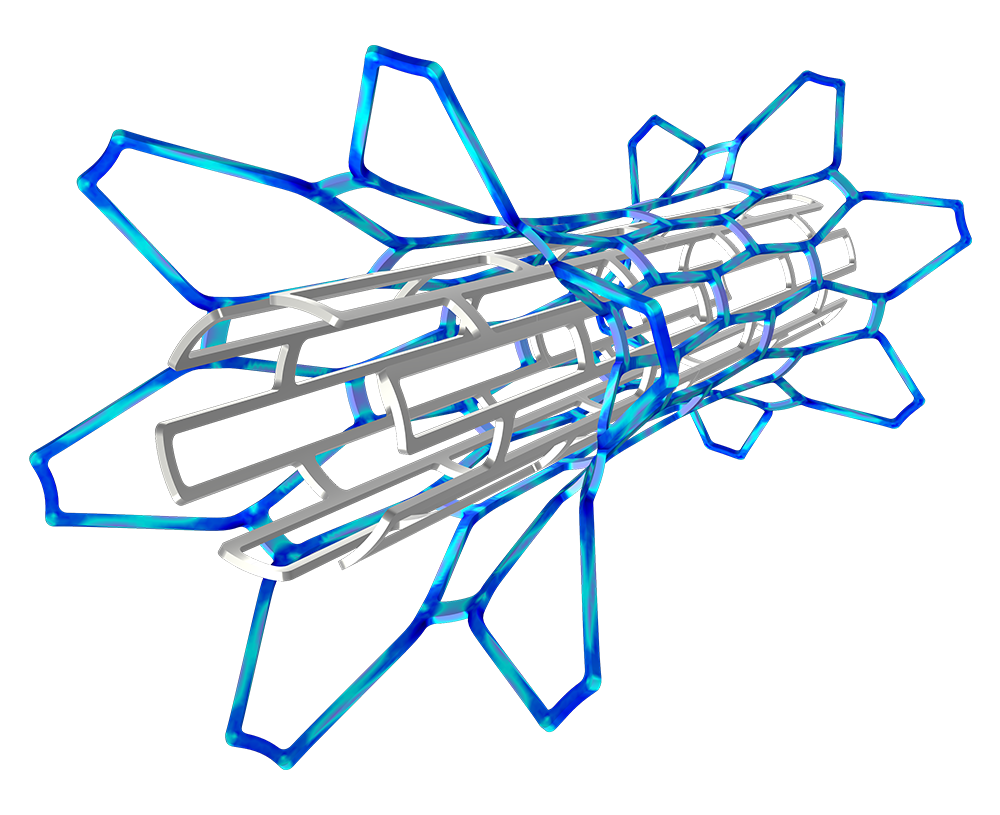
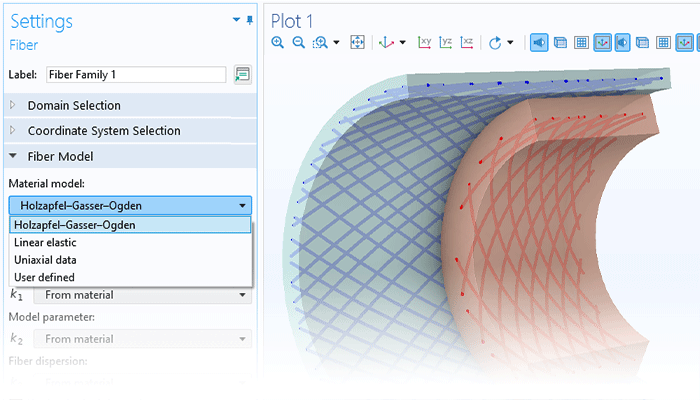
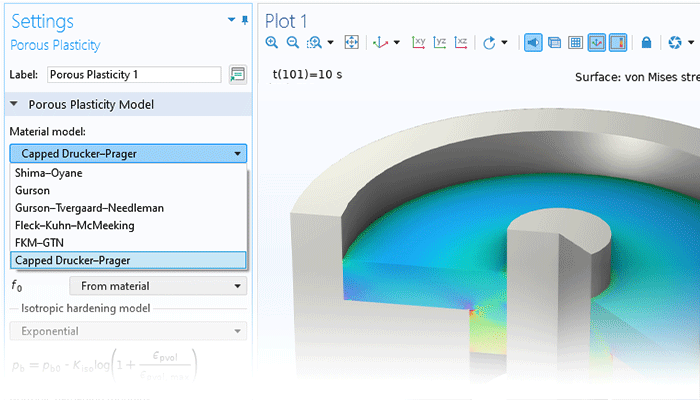
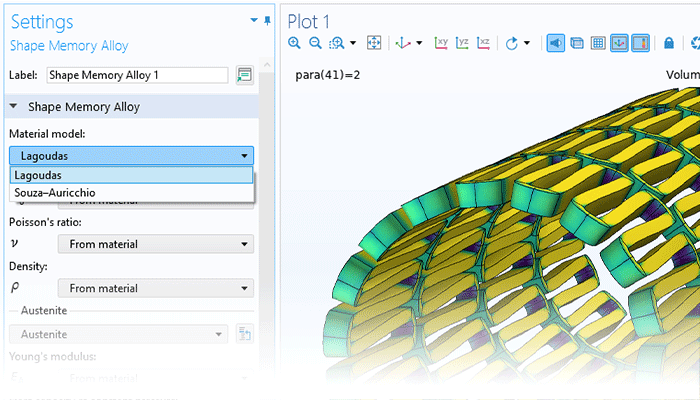
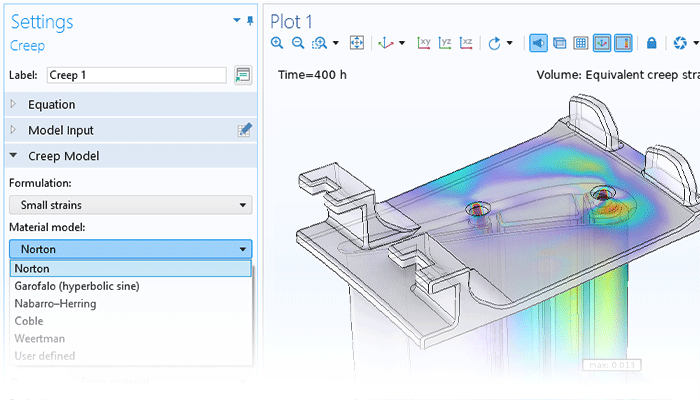
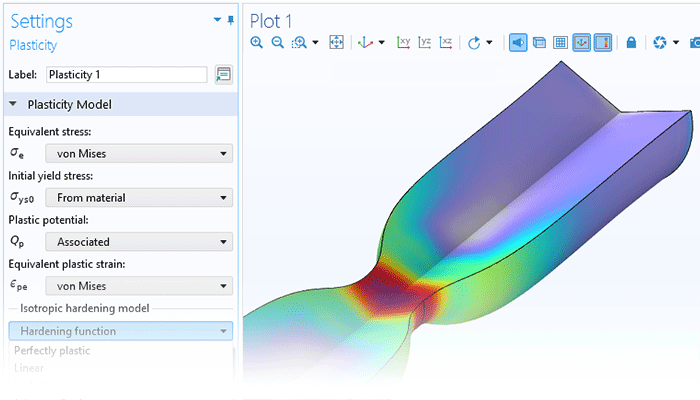
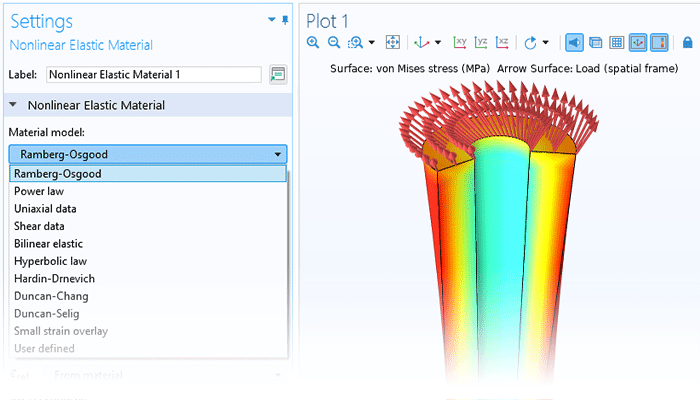
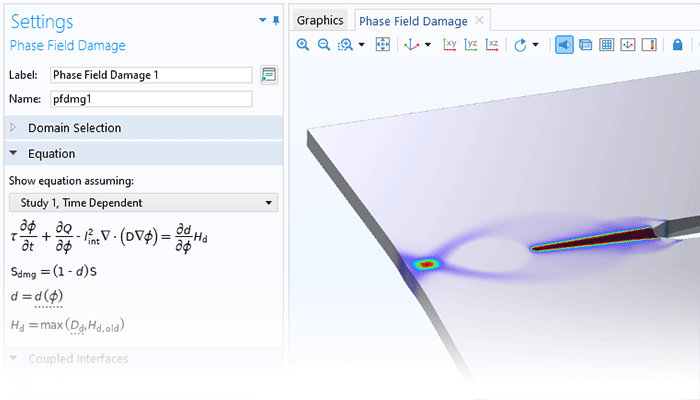
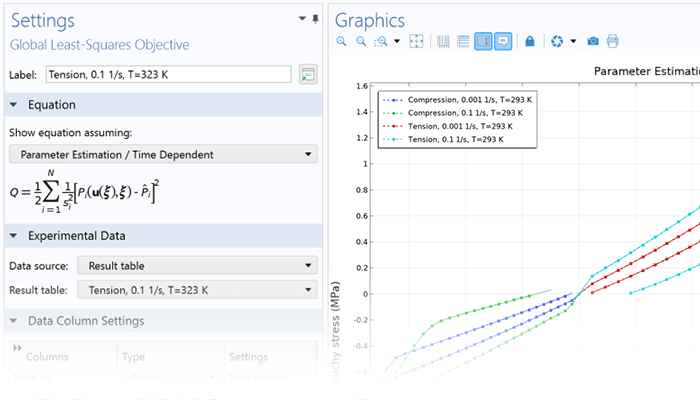
非线性材料建模功能为“结构力学模块”或“MEMS 模块”提供了全面的增强。通过将线弹性、超弹性或非线性弹性材料与非线性效应（如塑性、蠕变、黏塑性或损伤）相结合，并利用 COMSOL Multiphysics®仿真软件的强大功能，用户只需单击几下鼠标即可轻松实现多物理场的耦合。此外，用户还能根据应力或应变不变量等来自定义材料模型，并制定个性化的流动规则、蠕变定律以及超弹性的应变能密度函数。
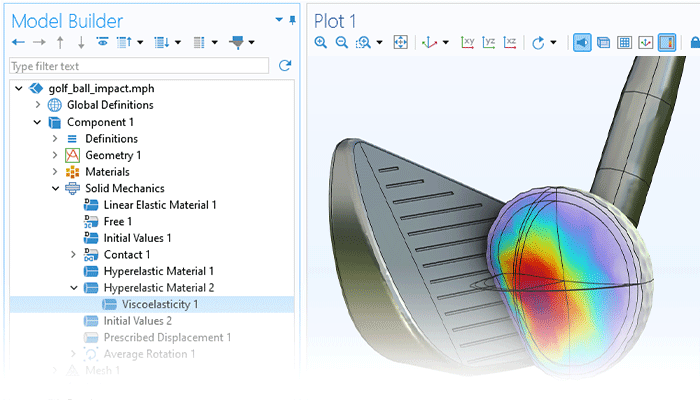
COMSOL Multiphysics®软件平台提供了内置的多物理场建模功能，适用于模拟热膨胀、孔隙压力、流-固耦合等各种多物理场现象。“非线性材料模块”中包含的所有结构材料均具备多物理场耦合分析的能力。
本模块提供多种材料模型
超弹性材料的本构定律基于应变能密度函数，能够准确模拟应力与应变之间存在非线性关系的材料。这种材料广泛应用于橡胶、泡沫和生物组织等领域。“非线性结构材料模块”提供多种不同的超弹性材料模型，同时支持用户根据特定需求定义自己的应变能密度函数。以下是一些可用的超弹性模型：
分析土壤、多孔金属和混凝土的塑性变形与传统金属塑性变形有着明显的区别。在多孔介质中，塑性变形的屈服函数和塑性势不仅与应力张量相关，还需要考虑静水压力的影响。本模块提供了以下多孔塑性模型：
形状记忆合金是一种特殊的材料，在经历了较大变形后，当加热到一定温度以上时仍能恢复到其原始形状。“非线性结构材料模块”包含的材料模型为奥氏体和马氏体的开始温度和结束温度以及重要的相变参数提供了必要的设置，其中包含两种常见的 SMA 模型：Lagoudas 和 Souza-Auricchio。
蠕变是材料在足够高的温度条件下受到应力（通常远小于屈服应力）时发生的一种非弹性瞬态变形。在 COMSOL Multiphysics®中，用户可以通过添加额外的蠕变节点来组合使用多个蠕变模型。黏塑性材料模型用于描述速率相关的非弹性变形，此类模型同时表现出蠕变特性。本软件支持多种黏塑性模型，其中聚合物黏塑性模型可以处理橡胶、聚乙烯等聚合物中的大黏塑性应变。以下是我们提供的一些常用蠕变和黏塑性模型：
许多材料都具有明显的弹性阶段，在此阶段内的变形是可恢复的，并且不受路径的影响。然而，当应力超过某一水平（即屈服极限）时，材料将会发生不可逆的永久塑性应变。金属和土壤等材料的这一特性常常通过弹塑性材料模型进行模拟。利用“非线性结构材料模块”提供的下列塑性模型，用户能够定义具有较小或较大塑性应变的弹塑性材料模型的属性，同时还能灵活设置屈服面和流动规则等。
与中等到大应变下表现为高度非线性的超弹性材料相比，非线性弹性材料即使在无限小应变下也呈现出非线性应力-应变关系。本模块提供以下非线性弹性模型：
此外，与岩土力学模块结合使用时，还提供其他一些材料模型。
即使在载荷不随时间变化的情况下，黏弹性材料受力后的变形也会随时间的推移而发生变化，许多聚合物和生物组织都表现出这种特性。在我们的“结构力学模块”和“MEMS 模块”中，采用了线性黏弹性作为一种常用的近似方法，其中应力与应变及其时间导数（应变率）呈线性关系。非线性弹性和超弹性材料模型可以扩展为包含黏弹性效应，以实现非线性应力-应变关系。本模块提供以下黏弹性模型：
准脆性材料（如混凝土或陶瓷）在受到机械载荷时会经历一系列变形过程。初始阶段表现为弹性变形；然而，当应力或应变超过临界水平时，材料将进入非线性断裂阶段。在达到这个临界值时，裂纹开始产生并扩展，最终导致材料发生断裂。裂纹的产生和扩展在脆性材料的破坏中起着重要的作用，这种特性可以通过多种理论进行描述。本模块提供以下损伤模型：
在建模预测过程中，非线性材料模型的准确性依赖于各种材料参数，每个参数的准确识别都至关重要。为了达到这一目标，需要使用广泛的实验结果数据集进行参数估计。借助“非线性结构材料模块”，可以通过应用非线性最小二乘参数估计技术和高效的基于梯度的优化求解器，使用实验数据来校准内置的和用户定义的材料模型。
COMSOL 是否能用于解决我的问题？
欢迎联系我们，我们的专业工程师可以协助您评估技术可行性，并根据使用场景推荐许可形式。
点击右侧的“联系 COMSOL”按钮，填写并提交信息，我们的工作人员将会尽快与您联系。
评估与试用 COMSOL®软件
