Estimation of Critical Parameters of Drop-Drop Electrocoalescence Using a Multiple-Drop System
Electrocoalescence is the phenomenon of coalescence of droplets suspended in an insulating liquid or in a gas under the action of an electric field. Electrocoalescence is considered a promising tool in many petrochemical industries for desalting crude oils. However, this technique suffers from some drawbacks such as short circuiting of electrodes, limitations on applied electric field and its frequency etc. It has been found experimentally that the drops don’t always coalesce in presence of electric field, but under certain conditions, they show noncoalescence phenomenon. A comprehensive prediction of the coalescence of drops in an electric field is lacking because of the complexity of the electrostatic and hydrodynamic interactions, as well as the difficulty in defining the electrical field strength that is actually experienced by the drops.
In this work, we have used COMSOL Multiphysics® software to understand and estimate the critical conditions of coalescence of two water drops suspended in oil in AC electric field. The coalescence parameters of the pair of the drops have been also studied in presence of additional water drops. The simulation is useful for estimating the condition under which coalescence will occur. It will also be useful in finding rate of coalescence, influence of surrounding drops on the coalescence of the given pair and the effect of surfactant, electric field intensity and nature ( DC/AC/Pulse DC) on the rate.
We consider a cylindrical vessel with insulating curved boundary. Two circular electrodes form the upper and the lower closures of the vessel. The vessel is filled with oil and two water drops are placed on the axis of the cylinder. Their positions are asymmetric with respect to the electrode. The schematic diagram of the system is shown in Figure 1. Since the problem is axi-symmetric, it can be transformed into two dimensional domain in cylindrical (r, z) coordinates. The domain is shown in part (ii) of the figure. We have used equation of motion and phase field equation to simulate the fluid part and track the interface and Meridional electric current equation to describe the potential distribution and the current density distribution in the system.
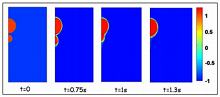
Results: Figure 2 shows the simulated images of the drops at different times after application of electric field of 90 kV/m. The drops are seen to coalesce. This is due to higher capillary pressure in the smaller drop compared to the larger drop. Next we consider coalescence among three drops. The position of the three drops is asymmetric with respect to the electrodes as shown in Figure 3. The middle drop coalesces with that drop which is farther away from the electrode than one which nearer.
The presence of other drops around the pair of drops under study, their sizes and the distance of the pair of drops from the electrodes, modify the coalescence tendency between that pair.
下载
- kulkarni_abstract.pdf - 0.18MB
